Download to read offline
Uploaded byОксана Бритова
аксиомы
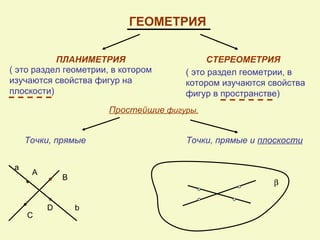
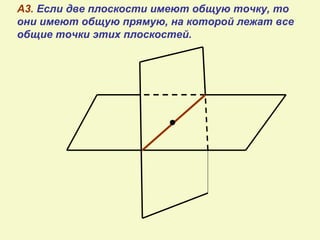
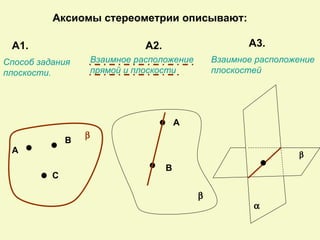
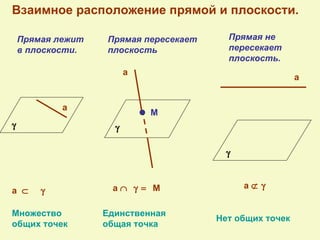
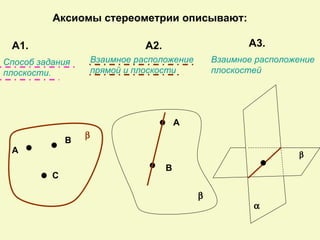
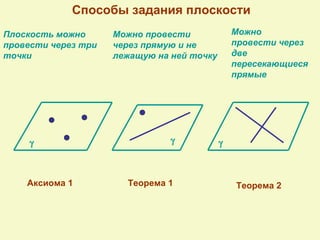
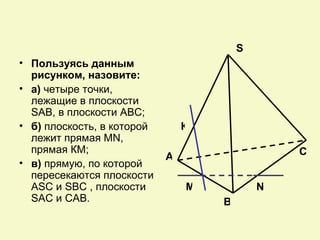
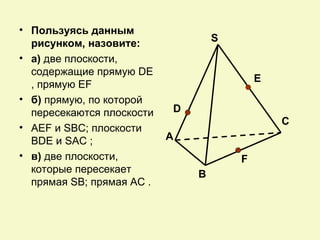
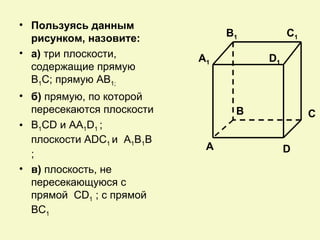
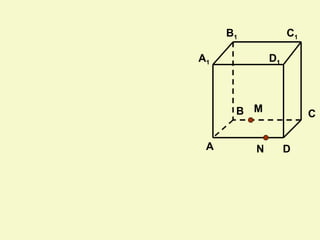
Документ посвящен аксиомам стереометрии и их применению к взаимному расположению точек, прямых и плоскостей в пространстве. Описаны основные аксиомы, такие как условия для проходящих прямых и плоскостей, а также взаимосвязи между ними. Приведены примеры для иллюстрации и закрепления теоретических положений.
More Related Content
аксиомы
- 1.
- 2. ГЕОМЕТРИЯ ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ ( это раздел геометрии, в котором ( это раздел геометрии, в изучаются свойства фигур на котором изучаются свойства плоскости) фигур в пространстве) Простейшие фигуры. Точки, прямые Точки, прямые и плоскости a А В β D b С
- 3. АКСИОМЫ планиметрия стереометрия Характеризуют взаимное А1. Через любые три точки, не расположение точек и прямых лежащие на одной прямой, проходит 1. Каждой прямой принадлежат плоскость, и притом только одна по крайней мере две точки А2. Если две точки прямой лежат 2. Имеются по крайней мере три в плоскости, то все точки прямой точки, не лежащие на одной прямой лежат в этой плоскости А3. Если две плоскости имеют 3. Через любые две точки проходит общую точку, то они имеют прямая, и притом только одна. общую прямую, на которой лежат Основное понятие геометрии все общие точки этих плоскостей. «лежать между» 4. Из трех точек прямой одна и только одна лежит между двумя другими.
- 4. А3. Если двеплоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
- 5. АКСИОМЫ планиметрия стереометрия Характеризуют взаимное А1. Через любые три точки, не расположение точек и прямых лежащие на одной прямой, проходит 1. Каждой прямой принадлежат плоскость, и притом только одна по крайней мере две точки А2. Если две точки прямой лежат в плоскости, то все точки прямой 2. Имеются по крайней мере три лежат в этой плоскости точки, не лежащие на одной прямой А3. Если две плоскости имеют 3. Через любые две точки проходит общую точку, то они имеют прямая, и притом только одна. общую прямую, на которой лежат Основное понятие геометрии все общие точки этих плоскостей. «лежать между» 4. Из трех точек прямой одна и только одна лежит между двумя другими.
- 6. Аксиомы стереометрии описывают: А1. А2. А3. Способ задания Взаимное расположение Взаимное расположение плоскости. прямой и плоскости плоскостей А β В А β В С β α
- 7. Взаимное расположение прямойи плоскости. Прямая лежит Прямая пересекает Прямая не в плоскости. плоскость пересекает плоскость. а а а М γ γ γ а∩ γ = М а⊄ γ а ⊂ γ Множество Единственная Нет общих точек общих точек общая точка
- 8. Аксиомы стереометрии описывают: А1. А2. А3. Способ задания Взаимное расположение Взаимное расположение плоскости. прямой и плоскости плоскостей А β В А β В С β α
- 9. Способы задания плоскости Плоскостьможно Можно провести Можно провести через три через прямую и не провести через точки лежащую на ней точку две пересекающиеся прямые γ γ γ Аксиома 1 Теорема 1 Теорема 2
- 10. S • Пользуясь данным рисунком, назовите: • а) четыре точки, лежащие в плоскости SAB, в плоскости АВС; • б) плоскость, в которой К лежит прямая MN, прямая КМ; C А • в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости М N SAC и CAB. В
- 11. • Пользуясь данным рисунком, назовите: S • а) две плоскости, содержащие прямую DE E , прямую EF • б) прямую, по которой пересекаются плоскости D С • AEF и SBC; плоскости BDE и SAC ; А • в) две плоскости, F которые пересекает В прямая SB; прямая AC .
- 12. • Пользуясь данным рисунком, назовите: B1 C1 • а) три плоскости, A1 D1 содержащие прямую В1С; прямую АВ1; • б) прямую, по которой пересекаются плоскости B C • B1CD и AA1D1 ; плоскости ADC1 и A1B1B A D ; • в) плоскость, не пересекающуюся с прямой CD1 ; с прямой BC1
- 13. B1 C1 A1 D1 B M C A N D