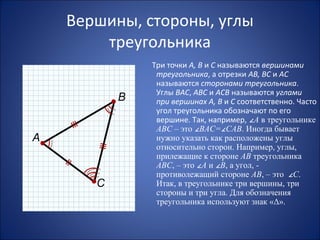
Документ описывает основные свойства треугольников в геометрии для 7 класса, включая определения, вершины, стороны и углы. Он также рассматривает равные треугольники и условия их существования. В заключение, подчеркивается, что треугольник формируется из трех неколлинеарных точек и может быть представлен в различных позициях.