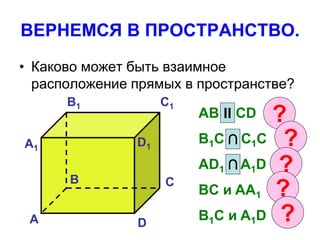
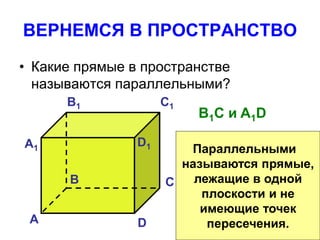
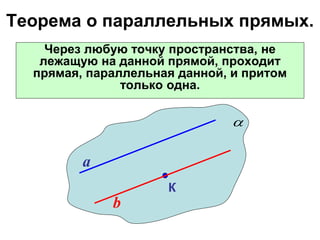
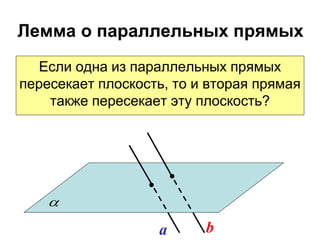
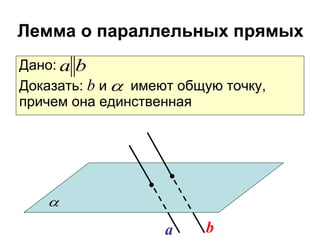
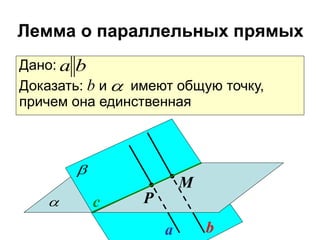
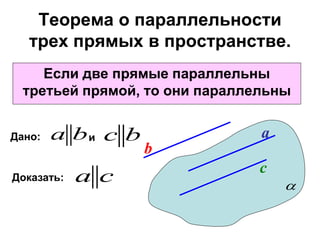
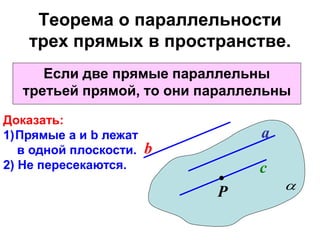
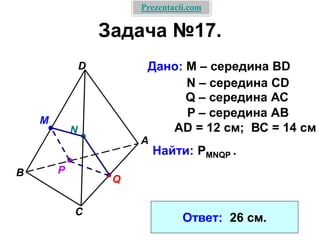
Документ охватывает взаимное расположение прямых на плоскости и в пространстве, а также определяет параллельные прямые. Включены аксиомы и теоремы о параллельности, а также их следствия и применения в геометрии. Приведена задача с расчетом длин отрезков и описаны условия для параллельности в пространстве.

1. МОУ СОШ №256 г.Фокино
Prezentacii.com

2.  Каково может быть взаимное
расположение двух прямых на
плоскости?
 Какие прямые в планиметрии
называются параллельными?

3.  Аксиома параллельных прямых - ?
Через точку, не лежащую на данной прямой,
проходит прямая, параллельная данной и притом
только одна

4.  Следствия аксиомы параллельных
прямых - ?
Если прямая пересекает одну из параллельных
прямых, то она пересекает и другую.
Если две прямые параллельны третьей
прямой, то они параллельны.

5. ВЕРНЕМСЯ В ПРОСТРАНСТВО.
• Каково может быть взаимное
расположение прямых в пространстве?
А
B C
D
А1
B1 C1
D1
AB и CD
B1C и C1C
AD1 и A1D
BC и AA1
B1C и A1D
II ?
∩ ?
∩ ?
?
?

6. ВЕРНЕМСЯ В ПРОСТРАНСТВО
• Какие прямые в пространстве
называются параллельными?
А
B C
D
А1
B1 C1
D1
B1C и A1D
Параллельными
называются прямые,
лежащие в одной
плоскости и не
имеющие точек
пересечения.

7. Теорема о параллельных прямых.
Через любую точку пространства, не
лежащую на данной прямой, проходит
прямая, параллельная данной, и притом
только одна.
К
a
b


8. …они лежат на параллельных
прямых
• Отрезки в пространстве называются
параллельными, если …
• Лучи в пространстве называются
параллельными, если …
Параллельные отрезки,
параллельные лучи
в пространстве.

9. Лемма о параллельных прямых
Если одна из параллельных прямых
пересекает плоскость, то и вторая прямая
также пересекает эту плоскость?
a b


10. Дано:
Доказать: b и имеют общую точку,
причем она единственная
a b

ba

Лемма о параллельных прямых

11. a b


с Р
М
Дано:
Доказать: b и имеют общую точку,
причем она единственная
ba

Лемма о параллельных прямых

12. Теорема о параллельности
трех прямых в пространстве.
Если две прямые параллельны
третьей прямой, то они параллельны
a
b
с

ba bcДано:
Доказать: ca
и

13. Теорема о параллельности
трех прямых в пространстве.
Если две прямые параллельны
третьей прямой, то они параллельны
a
b
с
Р 
Доказать:
1)Прямые а и b лежат
в одной плоскости.
2) Не пересекаются.

14. Задача №17.
Дано: М – середина BD
A
B
D
C
N
M
Р
Q
N – середина CD
Q – середина АС
P – середина АВ
АD = 12 см; ВС = 14 см
Найти: PMNQP .
Ответ: 26 см.
Prezentacii.com