1. Γ.Φ.

2. Τι είναι οι ζδρεσ
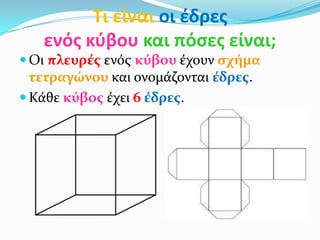
ενόσ κφβου και πόςεσ είναι;
 Οι πλευρϋσ ενόσ κύβου ϋχουν ςχόμα
τετραγώνου και ονομϊζονται ϋδρεσ.
 Κϊθε κύβοσ ϋχει 6 ϋδρεσ.

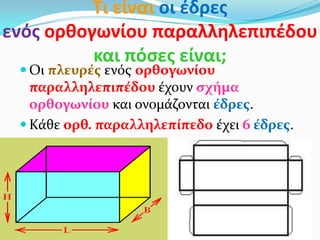
3. Τι είναι οι ζδρεσ
ενόσ ορκογωνίου παραλλθλεπιπζδου
και πόςεσ είναι;
 Οι πλευρϋσ ενόσ ορθογωνύου
παραλληλεπιπϋδου ϋχουν ςχόμα
ορθογωνύου και ονομϊζονται ϋδρεσ.
 Κϊθε ορθ. παραλληλεπύπεδο ϋχει 6 ϋδρεσ.

4. Σε τι διαφζρει ο κφβοσ
από το ορκογώνιο παραλλθλεπίπεδο;
 Στον κύβο όλεσ οι ϋδρεσ εύναι τετρϊγωνα
και εύναι ύςεσ μεταξύ τουσ.
 Στο ορθογώνιο παραλληλεπύπεδο οι ϋδρεσ
εύναι ορθογώνια παραλληλόγραμμα και
μόνο οι απϋναντι ϋδρεσ εύναι ύςεσ ανϊ δύο.

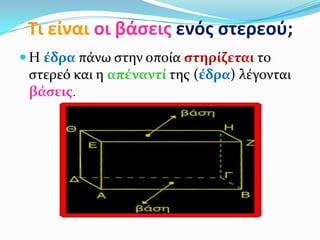
5. Τι είναι οι βάςεισ ενόσ ςτερεοφ;
 Η ϋδρα πϊνω ςτην οπούα ςτηρύζεται το
ςτερεό και η απϋναντύ τησ (ϋδρα) λϋγονται
βϊςεισ.

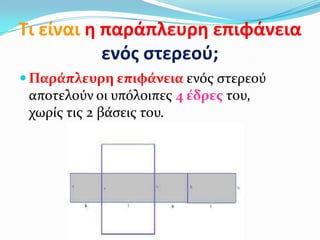
6. Τι είναι θ παράπλευρθ επιφάνεια
ενόσ ςτερεοφ;
 Παρϊπλευρη επιφϊνεια ενόσ ςτερεού
αποτελούν οι υπόλοιπεσ 4 ϋδρεσ του,
χωρύσ τισ 2 βϊςεισ του.

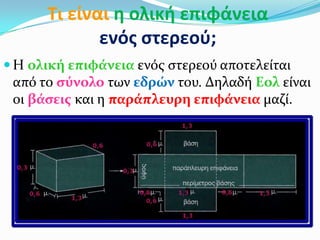
7. Τι είναι θ ολικι επιφάνεια
ενόσ ςτερεοφ;
 Η ολικό επιφϊνεια ενόσ ςτερεού αποτελεύται
από το ςύνολο των εδρών του. Δηλαδό Εολ εύναι
οι βϊςεισ και η παρϊπλευρη επιφϊνεια μαζύ.

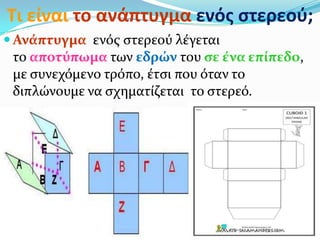
8. Τι είναι το ανάπτυγμα ενόσ ςτερεοφ;
 Ανϊπτυγμα ενόσ ςτερεού λϋγεται
το αποτύπωμα των εδρών του ςε ϋνα επύπεδο,
με ςυνεχόμενο τρόπο, ϋτςι που όταν το
διπλώνουμε να ςχηματύζεται το ςτερεό.

9. Πώσ υπολογίηεται το Εολ ενόσ κφβου;
Το εμβαδό τησ ολικόσ επιφϊνειασ (Εολ) ενόσ
κύβου υπολογύζεται ωσ εξόσ:
 Υπολογύζω πρώτα το εμβαδό μιασ ϋδρασ,
πολλαπλαςιϊζοντασ μια ακμό (α) με τον
εαυτό τησ και ςτη ςυνϋχεια πολλαπλαςιϊζω το
αποτϋλεςμα επύ 6 (επειδό ο κύβοσ αποτελεύται
από 6 ύςεσ ϋδρεσ).

10. Πώσ υπολογίηεται το Εολ ενόσ ορκ. παρ/δου;
Το εμβαδό τησ ολικόσ επιφϊνειασ (Εολ) ενόσ
ορθ. παραλληλεπιπϋδου υπολογύζεται ωσ εξόσ:
 Υπολογύζω πρώτα το εμβαδό καθεμιϊσ από τισ
3 διαφορετικϋσ ϋδρεσ του ορθ. παρ/δου,
προςθϋτω τα τρύα εμβαδϊ και ςτη ςυνϋχεια
πολλαπλαςιϊζω το αποτϋλεςμα επύ 2.

11. Τφποι εμβαδοφ
Εολ =
Ολικό εμβαδό =
Εμβαδό κύβου
Εολ =
Γιϊννησ Φερεντύνοσ
Εμβαδό ορθογωνίου παραλληλεπιπέδου
Εολ =
μ = μόκοσ
π = πλϊτοσ
υ= ύψοσ
Επαρ + Ε2β
Εμβαδό παρϊπλευρησ επιφϊνειασ +
Εμβαδό 2 βϊςεων
(περύμετροσ βϊςησ) . (ύψοσ) + Ε2β =
(μ + π + μ + π) * υ + 2 * μ * π
Επαρ + Ε2β = 4*α*α + 2*α*α =6*α*α = 6*α²