More Related Content
PDF
PDF
PDF
PDF
PPTX
【DL輪読会】言語以外でのTransformerのまとめ (ViT, Perceiver, Frozen Pretrained Transformer etc) PDF
PPTX
PDF
What's hot
PDF
SSII2022 [SS1] ニューラル3D表現の最新動向〜 ニューラルネットでなんでも表せる?? 〜 PDF
PDF
Skip Connection まとめ(Neural Network) PPTX
PDF
PDF
SSII2022 [SS2] 少ないデータやラベルを効率的に活用する機械学習技術 〜 足りない情報をどのように補うか?〜 PDF
PDF
機械学習による統計的実験計画(ベイズ最適化を中心に) PDF
BlackBox モデルの説明性・解釈性技術の実装 PDF
PPTX
PDF
PPTX
PDF
PDF
PDF
PPTX
Curriculum Learning (関東CV勉強会) PDF
PDF
PPTX
【DL輪読会】Efficiently Modeling Long Sequences with Structured State Spaces Similar to Sparse Codingをなるべく数式を使わず理解する(PCAやICAとの関係)
PDF
東京都市大学 データ解析入門 4 スパース性と圧縮センシング1 PDF
PDF
PPTX
PDF
PDF
PFI Christmas seminar 2009 PDF
(文献紹介) 画像復元:Plug-and-Play ADMM PPTX
2015年12月PRMU研究会 対応点探索のための特徴量表現 PDF
東京都市大学 データ解析入門 5 スパース性と圧縮センシング 2 PDF
ML: Sparse regression CH.13 PPTX
スパース性に基づく機械学習(機械学習プロフェッショナルシリーズ) 3.3節と3.4節 PPTX
PDF
コンピュータビジョン最先端ガイド6 第2章:4~4.2節 PDF
PDF
PDF
PDF
PDF
畳み込みネットワークによる高次元信号復元と異分野融合への展開 PPTX
多層NNの教師なし学習� コンピュータビジョン勉強会@関東 2014/5/26 PPTX
More from Teppei Kurita
PDF
PPTX
カメラでの偏光取得における円偏光と位相遅延の考え方 PPTX
論文解説:スマホカメラを用いたBRDFパラメータ取得技術(非DNN)「Two-Shot SVBRDF Capture for Stationary Mat... PPTX
PPTX
BRDF Model (English version) PPTX
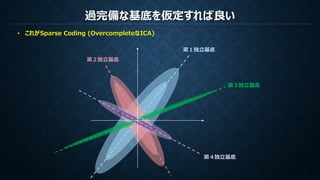
Sparse Codingをなるべく数式を使わず理解する(PCAやICAとの関係)
- 1.
- 2.
背景
• 10年前に画像処理界隈で流行っていたSparse Codingを改めて振り返ってみる
•結局なんだったんだっけ?
• 数式をなるべく使わない
• 何か気づきがあるかも
https://towardsdatascience.com/cyber-security-sparse-coding-and-anomaly-detection-1b0508d041c8
https://www.sciencedirect.com/topics/engineering/sparse-coding
Sparse Codingのイメージ(ノイズ除去等によく使われていた)
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
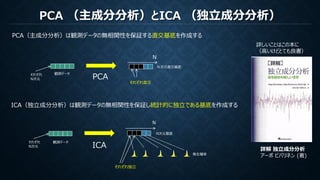
PCA (主成分分析)とICA (独立成分分析)
詳解独立成分分析
アーポ ビバリネン (著)
詳しいことはこの本に
(高いけどとても良書)
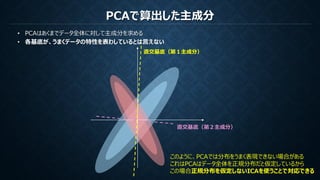
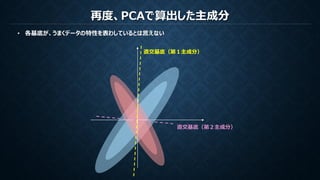
PCAそれぞれ
N次元
観測データ
N
それぞれ
N次元
観測データ
N
ICA
N次元直交基底
N次元基底
それぞれ直交
発生確率
それぞれ独立
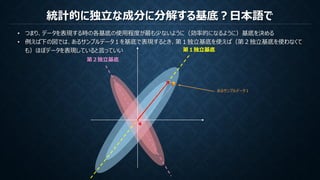
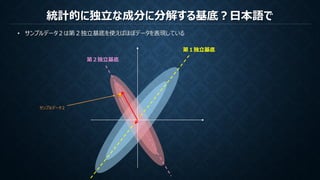
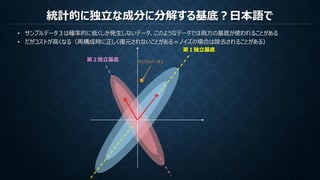
PCA(主成分分析)は観測データの無相関性を保証する直交基底を作成する
ICA(独立成分分析)は観測データの無相関性を保証し統計的に独立である基底を作成する
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
SPARSE CODING(ノイズ除去タスク、数式あり)
min
𝐃𝐃∈𝐶𝐶,𝐀𝐀
�
𝑖𝑖=1
𝑛𝑛
𝛂𝛂𝑖𝑖 𝑝𝑝𝑠𝑠. 𝑡𝑡. 𝐲𝐲𝑖𝑖 − 𝐃𝐃𝛂𝛂𝑖𝑖 2
2
≤ 𝜀𝜀
1α 2α nα
min
𝛂𝛂𝑖𝑖∈ℜ𝑘𝑘
𝛂𝛂𝑖𝑖 𝑝𝑝 𝑠𝑠. 𝑡𝑡. 𝐲𝐲𝑖𝑖 − 𝐃𝐃𝛂𝛂𝑖𝑖 2
2
≤ 𝜀𝜀
基底k
最適化式
最適化式
学習(ノイズ)
パッチ𝐲𝐲𝑖𝑖
再構成パッチ𝐃𝐃𝛂𝛂𝑖𝑖
𝐶𝐶:ℜ 𝑚𝑚×𝑘𝑘
𝑛𝑛:画像全体のパッチ数(通常画素数と同じ)
𝑘𝑘:基底の数(通常400程度)
𝑚𝑚:パッチ(基底)内の画素数(通常8×8=64程度)
𝐃𝐃:基底の集合(基底数𝑘𝑘×基底の画素数𝑚𝑚)
𝐀𝐀=[𝛂𝛂1, … , 𝛂𝛂𝑛𝑛]はℜ𝑘𝑘×𝑛𝑛の行列
𝐲𝐲𝑖𝑖:ノイズ画像𝐲𝐲の𝑖𝑖番目のパッチ
𝛂𝛂𝑖𝑖:𝐲𝐲𝑖𝑖に使用される基底𝐃𝐃の係数
𝐑𝐑𝑖𝑖:画像中のパッチ𝑖𝑖の正しい場所を示す2値行列(ℜ𝑛𝑛×𝑚𝑚
)
𝜒𝜒𝑚𝑚
2
分布の累積分布関数𝐹𝐹𝑚𝑚を用いて、𝜀𝜀を𝜎𝜎2 𝐹𝐹𝑚𝑚
−1
(𝜏𝜏)として選択する(通常𝜏𝜏=0.9)
(𝜎𝜎:ノイズの標準偏差)
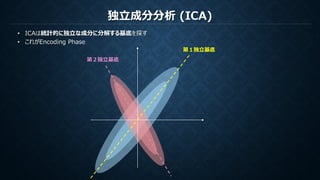
Encoding Phase
Decoding Phase
目的:基底の集合Dを学習パッチの集合𝐲𝐲から作成
目的:係数(基底の重み)𝛂𝛂𝑖𝑖をノイズパッチ𝐲𝐲𝑖𝑖から作成
𝛂𝛂𝑖𝑖のpノルムの合計を最小化
ノイズパッチ𝐲𝐲𝑖𝑖 再構成パッチ𝐃𝐃𝛂𝛂𝑖𝑖𝛂𝛂𝑖𝑖それぞれのpノルムを最小化
パッチ画素n
1. Dを固定し、Matching Pursuit等でαを求める
2. αを固定し、Lasso-LARS等で式を最小化するDを求める
収束するまで繰り返し
Matching Pursuit等でαを求める
※本来はこれに正則化項が入る
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
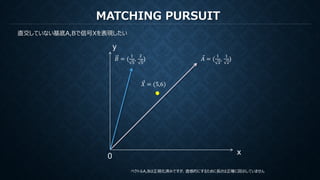
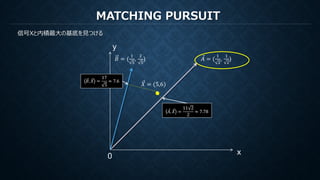
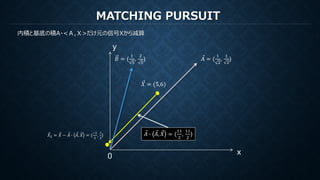
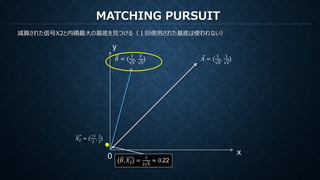
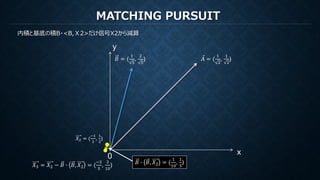
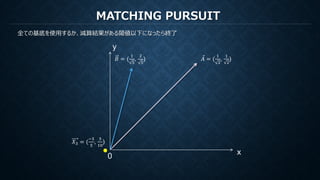
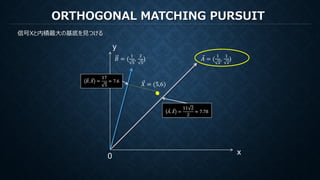
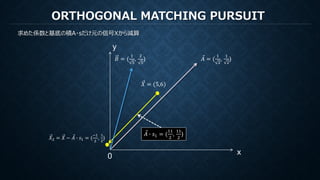
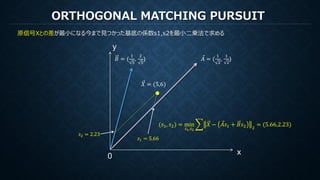
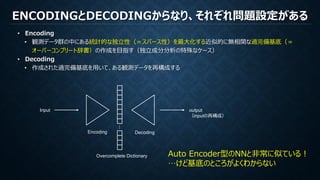
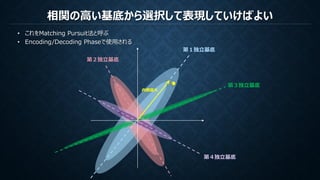
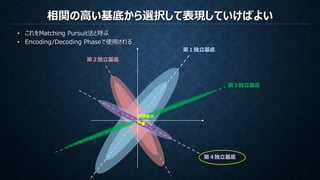
MATCHING PURSUIT
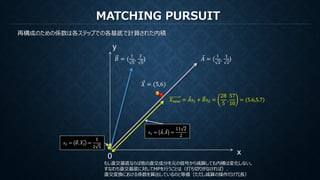
再構成のための係数は各ステップでの各基底で計算された内積
x
y
0
𝑠𝑠2 =𝐵𝐵, 𝑋𝑋2 =
1
2 5
𝑠𝑠1 = ⃗𝐴𝐴, ⃗𝑋𝑋 =
11 2
2
𝑋𝑋𝑛𝑛𝑛𝑛𝑛𝑛 = ⃗𝐴𝐴𝑠𝑠1 + 𝐵𝐵𝑠𝑠2 =
28
5
,
57
10
= (5.6,5.7)
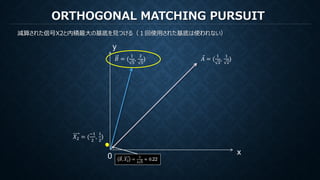
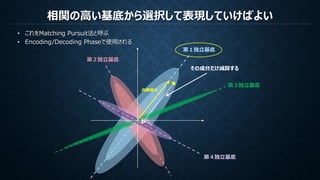
もし直交基底ならば他の直交成分を元の信号から減算しても内積は変化しない。
すなわち直交基底に対してMPを行うことは(打ち切りがなければ)、
直交変換における係数を算出しているのと等価(ただし減算の操作だけ冗長)
𝐵𝐵 = (
1
5
,
2
5
) ⃗𝐴𝐴 = (
1
2
,
1
2
)
𝑋𝑋 = (5,6)
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.









![SPARSE CODING(ノイズ除去タスク、数式あり)
min
𝐃𝐃∈𝐶𝐶,𝐀𝐀
�
𝑖𝑖=1
𝑛𝑛
𝛂𝛂𝑖𝑖 𝑝𝑝 𝑠𝑠. 𝑡𝑡. 𝐲𝐲𝑖𝑖 − 𝐃𝐃𝛂𝛂𝑖𝑖 2
2
≤ 𝜀𝜀
1α 2α nα
min
𝛂𝛂𝑖𝑖∈ℜ𝑘𝑘
𝛂𝛂𝑖𝑖 𝑝𝑝 𝑠𝑠. 𝑡𝑡. 𝐲𝐲𝑖𝑖 − 𝐃𝐃𝛂𝛂𝑖𝑖 2
2
≤ 𝜀𝜀
基底k
最適化式
最適化式
学習(ノイズ)
パッチ𝐲𝐲𝑖𝑖
再構成パッチ𝐃𝐃𝛂𝛂𝑖𝑖
𝐶𝐶:ℜ 𝑚𝑚×𝑘𝑘
𝑛𝑛:画像全体のパッチ数(通常画素数と同じ)
𝑘𝑘:基底の数(通常400程度)
𝑚𝑚:パッチ(基底)内の画素数(通常8×8=64程度)
𝐃𝐃:基底の集合(基底数𝑘𝑘×基底の画素数𝑚𝑚)
𝐀𝐀=[𝛂𝛂1, … , 𝛂𝛂𝑛𝑛]はℜ𝑘𝑘×𝑛𝑛の行列
𝐲𝐲𝑖𝑖:ノイズ画像𝐲𝐲の𝑖𝑖番目のパッチ
𝛂𝛂𝑖𝑖:𝐲𝐲𝑖𝑖に使用される基底𝐃𝐃の係数
𝐑𝐑𝑖𝑖:画像中のパッチ𝑖𝑖の正しい場所を示す2値行列(ℜ𝑛𝑛×𝑚𝑚
)
𝜒𝜒𝑚𝑚
2
分布の累積分布関数𝐹𝐹𝑚𝑚を用いて、𝜀𝜀を𝜎𝜎2 𝐹𝐹𝑚𝑚
−1
(𝜏𝜏)として選択する(通常𝜏𝜏=0.9)
(𝜎𝜎:ノイズの標準偏差)
Encoding Phase
Decoding Phase
目的:基底の集合Dを学習パッチの集合𝐲𝐲から作成
目的:係数(基底の重み)𝛂𝛂𝑖𝑖をノイズパッチ𝐲𝐲𝑖𝑖から作成
𝛂𝛂𝑖𝑖のpノルムの合計を最小化
ノイズパッチ𝐲𝐲𝑖𝑖 再構成パッチ𝐃𝐃𝛂𝛂𝑖𝑖𝛂𝛂𝑖𝑖それぞれのpノルムを最小化
パッチ画素n
1. Dを固定し、Matching Pursuit等でαを求める
2. αを固定し、Lasso-LARS等で式を最小化するDを求める
収束するまで繰り返し
Matching Pursuit等でαを求める
※本来はこれに正則化項が入る](https://image.slidesharecdn.com/sparsecoding-200414044010/85/Sparse-Coding-PCA-ICA-24-320.jpg)