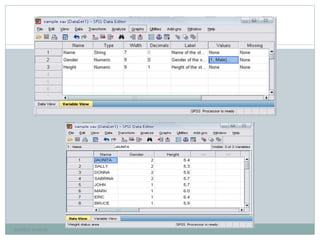
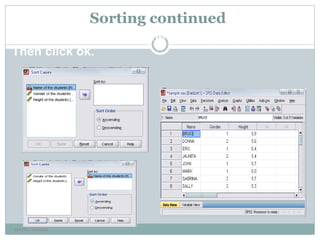
SPSS (Statistical Package for the Social Sciences) is software used for statistical analysis. It was first released in 1968 and was originally developed for analyzing social science data but is now used in other fields like health sciences and marketing. SPSS can perform a variety of statistical analyses like descriptive statistics, bivariate statistics, prediction analyses, and can present results graphically. It uses a four window interface of a data editor, output viewer, syntax editor, and script window. Users enter and manage data in the data editor which has both a data view and variable view. SPSS is useful for summarizing, exploring, and testing hypotheses with data.

1. neethu asokan

2.  The software name stands for Statistical
Package for the Social Sciences (SPSS)
 Reflecting the original market, although the
software is now popular in other fields as
well, including the health sciences and
marketing.
 Used to analyze data collected from surveys,
tests, observations, etc. It can perform a
variety of data analyses and presentation
functions, including statistical analysis and
graphical presentation of data.
neethu asokan

3. Statistics included in the base
software:
 Descriptive statistics: Cross tabulation,
Frequencies, Descriptives, Explore,
Descriptive Ratio Statistics
 Bivariate statistics: Means, t-test,
ANOVA, Correlation (bivariate, partial,
distances), Nonparametric tests
 Prediction for numerical outcomes:
Linear regression
 Prediction for identifying groups: Factor
analysis, cluster analysis (two-step, K-
means, hierarchical), Discriminant
neethu asokan

4. History
 The software was released in its first version
in 1968 as the Statistical Package for the
Social Sciences (SPSS) after being developed
by Norman H. Nie, Dale H. Bent, and C.
Hadlai Hull
 Those principals incorporated as SPSS Inc.
in 1975
neethu asokan

5. Objectives
 About the four-windows in SPSS
 The basics of managing data files
 The basic analysis in SPSS
neethu asokan

6. The Four Windows: Data Editor
 Data Editor
Spreadsheet-like system for defining,
entering, editing, and displaying data.
Extension of the saved file will be “sav.”
 Output Viewer
Displays output and errors. Extension
of the saved file will be “spv.”
neethu asokan

7.  Syntax Editor
Text editor for syntax composition.
Extension of the saved file will be “sps.”
 Script Window
Provides the opportunity to write full-
blown programs, in a BASIC-like language.
Text editor for syntax composition.
Extension of the saved file will be “sbs.”
neethu asokan

8. The basics of managing data files
 Opening SPSS
 The default window will have the data
editor
 There are two sheets in the window:
 1. Data view 2. Variable view
neethu asokan

9. Data View window
The Data View window
 This sheet is visible when you first open the Data
Editor and this sheet contains the data
 Click on the tab labeled Variable View
neethu asokan

10. Variable View window
 This sheet contains information about the data
set that is stored with the dataset
Name
 The first character of the variable name must be
alphabetic
 Variable names must be unique, and have to be
less than 64 characters.
 Spaces are NOT allowed.
neethu asokan

11. Variable View window
 Type
Click on the ‘type’ box. The two basic
types of variables that you will use are
numeric and string. This column enables you
to specify the type of variable.
 Width
Width allows you to determine the
number of characters SPSS will allow to be
entered for the variable
neethu asokan

12.  Decimals
Number of decimals
It has to be less than or equal to 16
 Label
You can specify the details of the variable
You can write characters with spaces up to 256
characters
 Values
This is used and to suggest which numbers
represent which categories when the variable
represents a category
neethu asokan

13. Defining the value labels
 Click the cell in the values column as shown below
 For the value, and the label, you can put up to 60
characters.
 After defining the values click add and then click OK.
neethu asokan

14. Example
neethu asokan

15. Example (solution)
neethu asokan

16. neethu asokan

17. Sorting the data
neethu asokan

18. Sorting continued
Double Click ‘Name of the students.’
Then click ok.
neethu asokan

19. References
 Kentaka Aruga (Feb 2008), Introduction To SPSS
(pdf).
 SPSS wikepedia, the free encyclopedia.
 SPSS_brief guide_21.pdf
 SPSS_ statistics_17.pdf
neethu asokan

20. Response Surface Methodology
neethu asokan

21. Definition of Response Surface Method
A simple function, such as linear or quadratic
polynomial, fitted to the data obtained from the
experiments is called a response surface, and the
approach is called the response surface method.
Response surface method is a collection of
statistical and mathematical techniques useful for
developing, improving, and optimizing processes.
Response surface method is a method for
constructing global approximations to system
behavior based on results calculated at various
points in the design space.
Box G.E.P. and Draper N.R.,1987
Myers R.H., 1995
Roux W.J.,1998
neethu asokan

22. RSM
 Response surface methodology (RSM) is a useful statistical
technique which has been applied in research into complex
variation process.
 The multiple regression and correlation analyses are used as
tools to assess the effects of two or more independent factors
on the dependent variable.
 Further more, the central composite design (CCD) of RSM has
been applied in the optimization of several biotechnological
and chemical processes (Jeong et al., 2009).
 Its main advantage is the reduced number of experimental runs
required to generate sufficient information for a statistically
acceptable results.
neethu asokan

23. History of Response Surface Method
1951 Box and Wilson - CCD
1959 Kiefer - Start of D-optimal Design
1960 Box and Behnken - Box-Behnken deign
1971 Box and Draper - D-optimal Design
1972 Fedorov - exchange algorithm
1974 Mitchell - D-optimal Design
1996 Burgee - design HSCT
1997 Ragon and Haftka - optimization of large wing structure
1998 Koch, Mavris, and Mistree - multi-level approximation
1999 Choi / Mavris – Robut, Reliablity-Based Design
Research of DOE
Application in
Optimization
App in Optimization & Reduce the
Approximation Error
neethu asokan

24. Concept of Response Surface Method
Original System
x1
x
2
-1 0 1
1
0
-1
DOE and Experiments
Black Boxed
System
Input
1x
2x
Response
y
RS Model
  jiiiiiiii xxbxbxbby
2
0
neethu asokan

25. Designs
 Three level factorial
 Box- Behnken
 Central Composite Design
 Doeblert designs
 Plackett- Burman JMP
In-
House
c
odes
Visual-
DOC SAS
SPS
S
MATLAB
Softwares
neethu asokan

26. Example
 Optimization of clavulanic acid production by Streptomyces
DAUFPE 3060 by response surface methodology.
 Clavulanic acid (CA) is a β-lactamase inhibitor that is
administered in combination with penicillin group antibiotics to
overcome certain types of antibiotic resistance.
 In order to optimize its production by the new isolate
Streptomyces DAUFPE 3060, the influence of two independent
variables, temperature and soybean flour concentration, on
clavulanic acid and biomass concentrations was investigated in
250 mL-Erlenmeyers according to central composite designs.
neethu asokan

27. Contin….
 A central composite design combined with RSM was used in
this work to select the best values of these two variables able to
optimize CA production by the same strain.
Method
Fermentation Spores
Liquid media/96h
Initial biomass concentration
Spores are stored by lyophilized in glycerol 10% v/v
Seed culture
neethu asokan

28. Cryotube with glycerol to 25ml of seed medium in 250ml flask
Incubated under shaker (28ºc, 200rpm, 24hrs.)
45ml of inoculum inoculated with 5ml of seed culture in 250ml flask
14 production runs, which lasted 168h
(orbital shaker/ 150rpm at different temp).
5ml of aliquots of
this suspension
with cells at
exponential phase
Flask containing
45ml production
media
neethu asokan

29. Experimental design
 The quadratic model to predict the optimal point was expressed
by the equation:
 where Ŷ represents the predicted value of the response variables,
b0 is the intercept coefficient, bi are the linear coefficients, bii
are the quadratic coefficients and bij are the interaction ones.
neethu asokan

30. Experimental design
 Experiments were planned so as to obtain quadratic models
able to describe the CA and biomass concentrations as
simultaneous functions of temperature and SF levels.
• The statistical significance of the regression coefficients was
determined by the Student's t-test, and the second-order
model equation was determined by the Fischer's test.
• The effects of unexplained variability in the observed
response due to extraneous factors were minimized by
randomizing the order of experiments
neethu asokan

31. neethu asokan

32. Experimental design conti………
 The experimental data of Table 2 were then used to make
regression analyses fitting both responses. The following
equations, where the variables take their coded values, express
the best models for CA and biomass concentrations,
respectively:
 where Ŷ1,Ŷ2 and x1 are CA, biomass and SF concentrations,
while x2 is temperature.
neethu asokan

33.  The simultaneous effects
of temperature and SF
concentration and their
interactions on the CA and
biomass productions are
better visualized in three-
dimensional (3-D) graph
projections (Figures 1 and
2) using the Response
Surface Methodology
(RSM).
Figure 1
neethu asokan

34. This means that the values
of both responses increased
up to a certain level when
both variables were raised.
As a result, there are two
regions of temperature (30-
34°C) and SF concentration
(35-45 g/L) where both
responses reach maximum
values.
Figure 2
neethu asokan

35. RESULT
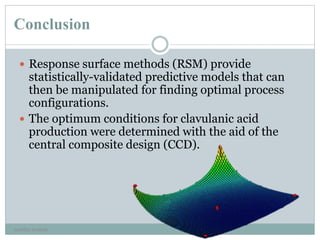
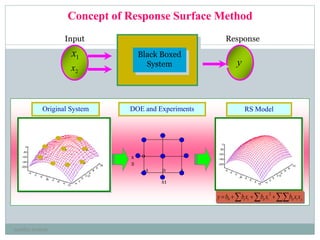
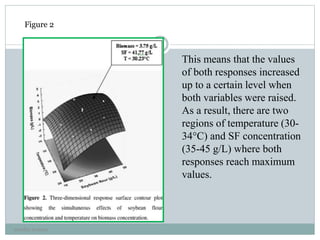
 Simultaneous regression by eqs. [3] and [4] provided maximum
predicted values of CA concentration (640 mg/L) at 33.0 °C and
SF = 37.5 g/L, and of biomass concentration (3.75 g/L) at 30.2 °C
and SF = 41.77 g/L, respectively. These predicted values are only
1.7 % higher and 3.8% lower than the experimental ones, thus
demonstrating the validity of the models employed.
neethu asokan

36.  Heavy Computation Problem
Approximation
 When Sensitivity is NOT Available
 Real / Numerical Experiment
 When the Batch Run is Impossible
 For Any System Which has Inputs
and Responses
 Easy to Implement
 Probabilistic Concept
 Noisy Responses or Environments
• Approximation Error
• Domain is Very Dominant
Advantages
Disadvantages
neethu asokan

37. Conclusion
 Response surface methods (RSM) provide
statistically-validated predictive models that can
then be manipulated for finding optimal process
configurations.
 The optimum conditions for clavulanic acid
production were determined with the aid of the
central composite design (CCD).
neethu asokan

38. References
 Daniela A. et.al., Optimization of clavulanic acid production by
Streptomyces DAUFPE 3060 by response surface methodology,
Braz. J. Microbiol. vol.42 no.2 São Paulo Apr./June 2011.
 Nadeem Irfan Bukhari et. Al.,Statistical Design of Experiments
on Fabrication of Starch Nanoparticles – A Case Study for
Application of Response Surface Methods (RSM).
 Response surface methodology,ppt.
 Tanarkorn Sukjit1& Vittaya Punsuvon1,Process Optimization Of
Crude Palm Oil Biodiesel Production By Response Surface
methodology, European International Journal of Science and
Technology Vol. 2 No. 7 September 2013.
neethu asokan

39. Thank
you
neethu asokan