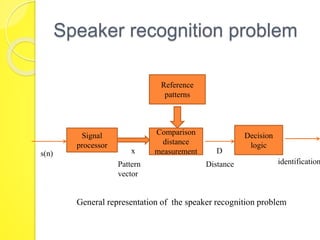
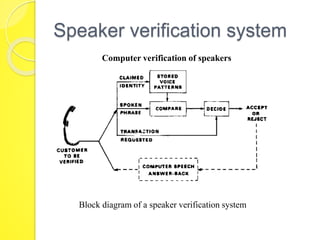
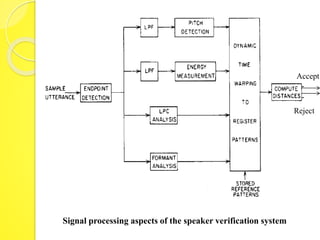
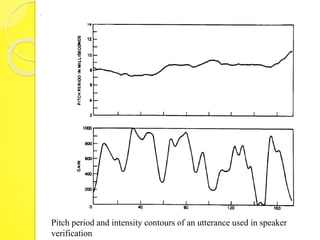
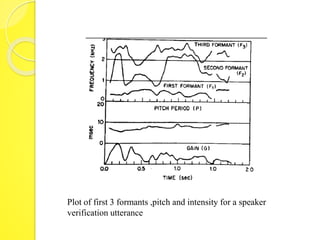
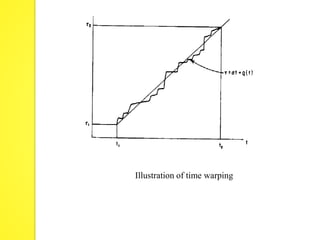
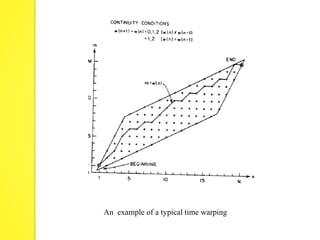
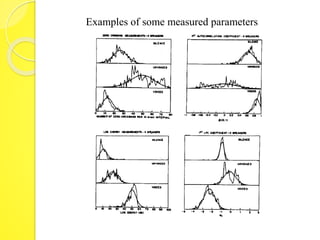
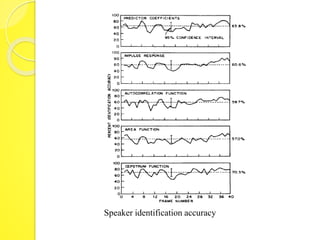
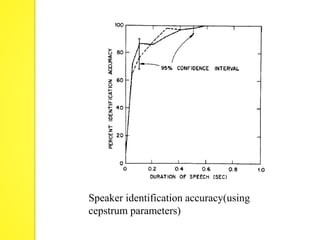
The document discusses speaker recognition systems, focusing on speaker verification and identification methods, which involve comparing speech patterns using digital processing techniques. It outlines the decision logic, error measurement processes, and the use of time warping to improve accuracy in matching speech patterns between claimed identities and stored references. The identification system requires multiple distance measurements and employs Gaussian distribution models to minimize error in assigning speaker identities.

1. SPEAKER RECOGNITION
SYSTEMS
BY
NAMRATHA D’CRUZ

2. Sub areas of speaker recognition
• Speaker verification system
• Speaker identification system

3. Speaker recognition problem
Signal
processor
Comparison
distance
measurement
Decision
logic
Reference
patterns
s(n) x D
Pattern Distance identification
vector
General representation of the speaker recognition problem

4.  A representation of the speech signal is obtained
using digital speech processing techniques
 which preserve the features of the speech signal
that are relevant to speaker identity.
 The resulting pattern is compared to previously
prepared reference patterns.
 Decision logic is used to make a choice among
available alternatives

5.  For speaker verification system if we denote the PDF
for the measurement vector x for the ith speaker as pi(x)
then the decision rule is given by
 Where ci is a constant for the ith speaker and pav(x) is
the average PDF for the measurement vector x
 For speaker identification system the decision rule is
given by

6. Speaker verification system
Computer verification of speakers
Block diagram of a speaker verification system

7.  Online digital speaker verification system was
developed by Rosenberg and others.
 The person wishing to be verified first enters his
claimed identity.
 On request from verification system utters his
verification phrase, and requests some transaction to
be made in the event he is verified.
 The spoken utterance is processed to obtain a
pattern which is compared to the stored reference
patterns for the claimed identity.

8.  On the basis of the transaction requested the error mix
constant (Ci) is determined .
 Based on error mix constant decision to accept or reject
is made.

9. Accept
Reject
Signal processing aspects of the speaker verification system

10. Signal Processing Parts Of The Speaker
Verification System
End point detection system: the sample
utterances which occurs somewhere within a pre
selected time interval is located.
Pitch detector : it is used to measure the pitch
contour of the utterance.
Energy measurements: short-time energy
measurements is made to give energy contours.

11. Signal Processing Parts Of The Speaker
Verification System
LPC analysis: is used to give predictor parameter
contours.
 LPC is a tool used for representing the spectral
envelope of a digital signal of speech
in compressed form, using the information of a linear
predictive model.
 Autocorrelation formulation method is used.
Formant analysis: estimates of the formant
locations is made.
LPF: 16hz low pass is used

12. Measurement contours for the test utterance “we
were away a year ago”
 Data are estimated at 100 times per second
 Smoothened by 16hz LPF, linear phase, FIR
digital filter.

13. Pitch period and intensity contours of an utterance used in speaker
verification

14. Plot of first 3 formants ,pitch and intensity for a speaker
verification utterance

15. Plots of the first 8 LPC coefficients for a speaker verification
utterance

16.  After the desired parametric representation has been
computed it is compared with the corresponding
reference patterns for the speaker whose identity is
claimed.
 Speaker is generally not able to speak at precisely the
same rate for different repetitions of the verification
phase.
 As a solution to this problem non linear time warping of
the input patterns is done to obtain the best possible
registration between stored pattern and the measured
patterns for speakers sample utterance.

17. Time warping
 The time scale t of a reference utterance is warped so
that significant events in some measurement contour a(t)
line up with the same significant events in the reference
contour r(t).
 The warping function is assumed to be
τ=α t+q(t)
Where
q(t) - is the non linear time warp function
α – average slope of the time warp function

18. Time warping
 Boundary condition s are imposed to ensure that the
beginning and ending points of both the sample and
reference utterances line up properly.
 The boundary conditions are:
τ1=α t1+q(t1)
τ2=α t2+q(t2)
 Function q(t) and constant α have to be chosen so as to
best align the measured contours.
 Simpler and faster solution is to utilize the method of
dynamic programming to optimally choose a constrained
warping function.

19. Illustration of time warping

20. Time warping
 Consider time warping for a pair of contours which are
sampled at a discrete set of points .
 Let the points be in the measured contour be labeled
n=1,2,…,N.
 Let the points in the reference contour be labeled
m=1,2,…,M.
 Time warping function w is chosen as
m=w(n)

21. Time warping
 The boundary on w(n) conditions are:
w(1) = 1 beginning points
w(N) = M ending points
 To limit the degree of non linearity of the warping
function mild continuity condition is imposed
 That the warping function w cannot change by more
than 2 grid points at any index n
w(n+1)-w(n) = 0,1,2 if w(n) != w(n-1)
= 1,2 if w(n) = w(n-1)
 Thus slope of warping function is either 0,1 or 2

22. Time warping
 To determine which of the conditions of equation to use
at grid index n requires the use of similarity measure
between the reference data measured at grid index n and
the test data measured at grid index m.
 The similarity measure is used to determine the path of
the warping function which minimizes the max total
distance ,subject to constraints of continuity equation.

23. An example of a typical time warping

24. Time warping
 Figure shows the possible grid coordinates (n,m) and a
warping function w(n).
 Consider N = 20 reference and M = 15 test utterance.
 Because of continuity constraints the warping function
must lie within the parallelogram.
 The final step is to compute overall distance measures
and then compare the distance to an appropriately
chosen threshold.
 The simplest distance contour measure is a normalized
sum of squares .

25. Distance measure
 For the jth measurement contour ,the distance dj would
be of the form
 Where ajs (i) is the value of the jth measurement contour
at time i
 ajr (i) ) is the value of the jth reference contour at time
i, and σaj(i) is the standard deviation of the jth
measurement at time i

26. Distance measure
 The distance function is given by
 Where wj is the jth weight chosen on the basis of the
effectiveness of the jth measurement in verifying the
speaker.

27. SPEAKER IDENTIFICATION
SYSTEMS
 Almost similar to the speaker verification systems
 Main difference is choice of parameters to make
distance measurements.
 N distance measurements have to be made rather than 1.
 Final decision is to choose the speaker whose reference
patterns are closest in distance to the sample patterns.

28. SPEAKER IDENTIFICATION
SYSTEMS
 More sophisticated and robust distance measure is used.
 Let x be an L- dimensional column vector representing
input pattern , in which the kth component of x is the kth
measurement.
 It is assumed that joint PDF of the measurements for the
ith speaker is a multi dimensional Gaussian distribution
with mean mi and covariance matrix wi. Thus ,the L-dimensional
Gaussian density function for x is given by

29. SPEAKER IDENTIFICATION SYSTEMS
 Where is the inverse of the matrix (assuming is
non singular),| | is the determinant of , and the t
denotes the transpose of a vector. The decision rule
which minimizes the probability of error states that the
measurement vector X should be assigned to class i if
 Where pi is the priori probability that belongs to the ith
class. Since ln y is a monotonically increasing function
of its argument y, the decision rule can be simplified as
Decide class i if

30. SPEAKER IDENTIFICATION SYSTEMS
 The bias term does not provide any advantage over the
decision rule . Thus the distance measure is defined as
 The mean and covariance vector is defined as

31. Examples of some measured parameters

32. Speaker identification accuracy

33. Speaker identification accuracy(using
cepstrum parameters)