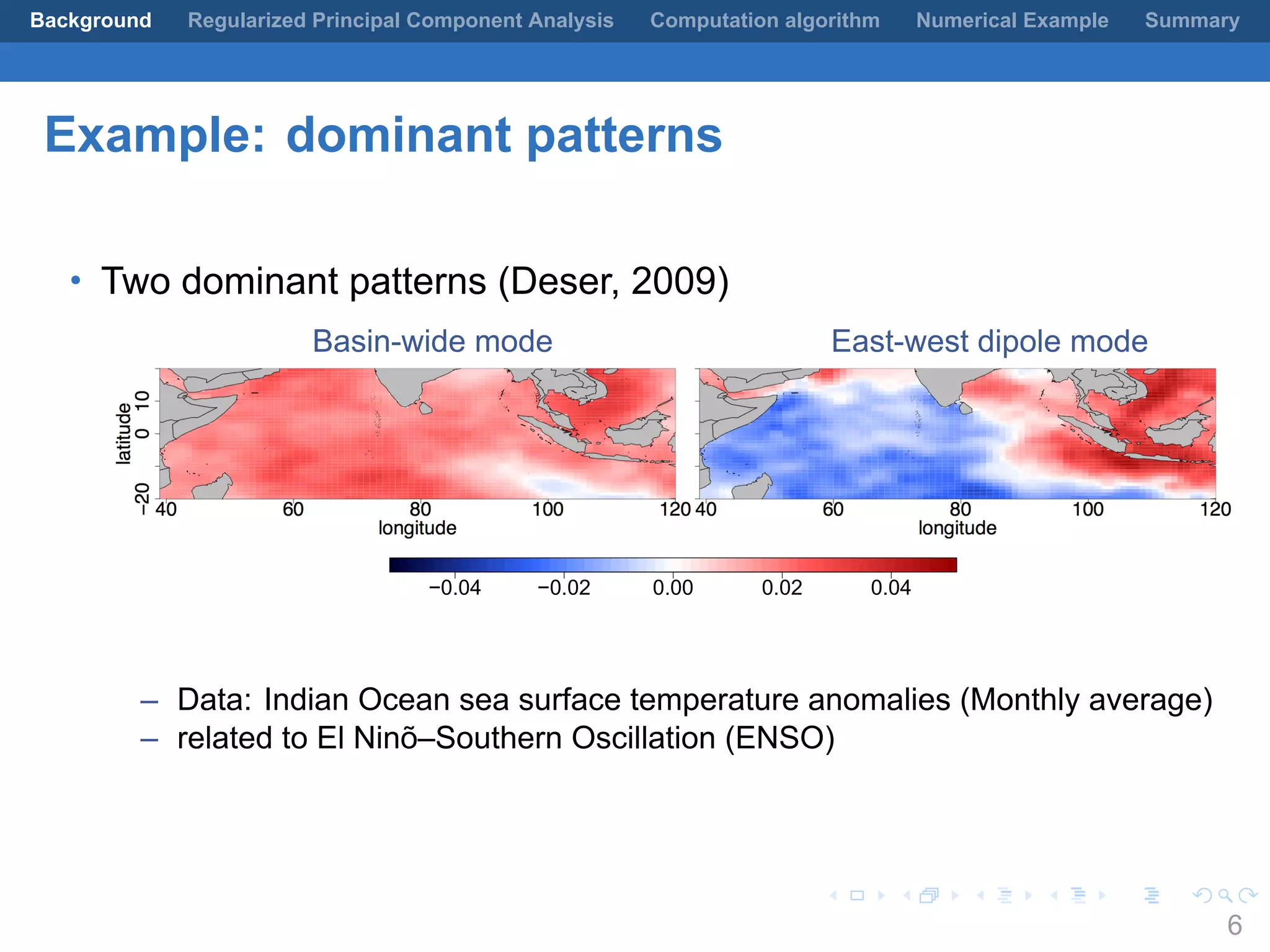
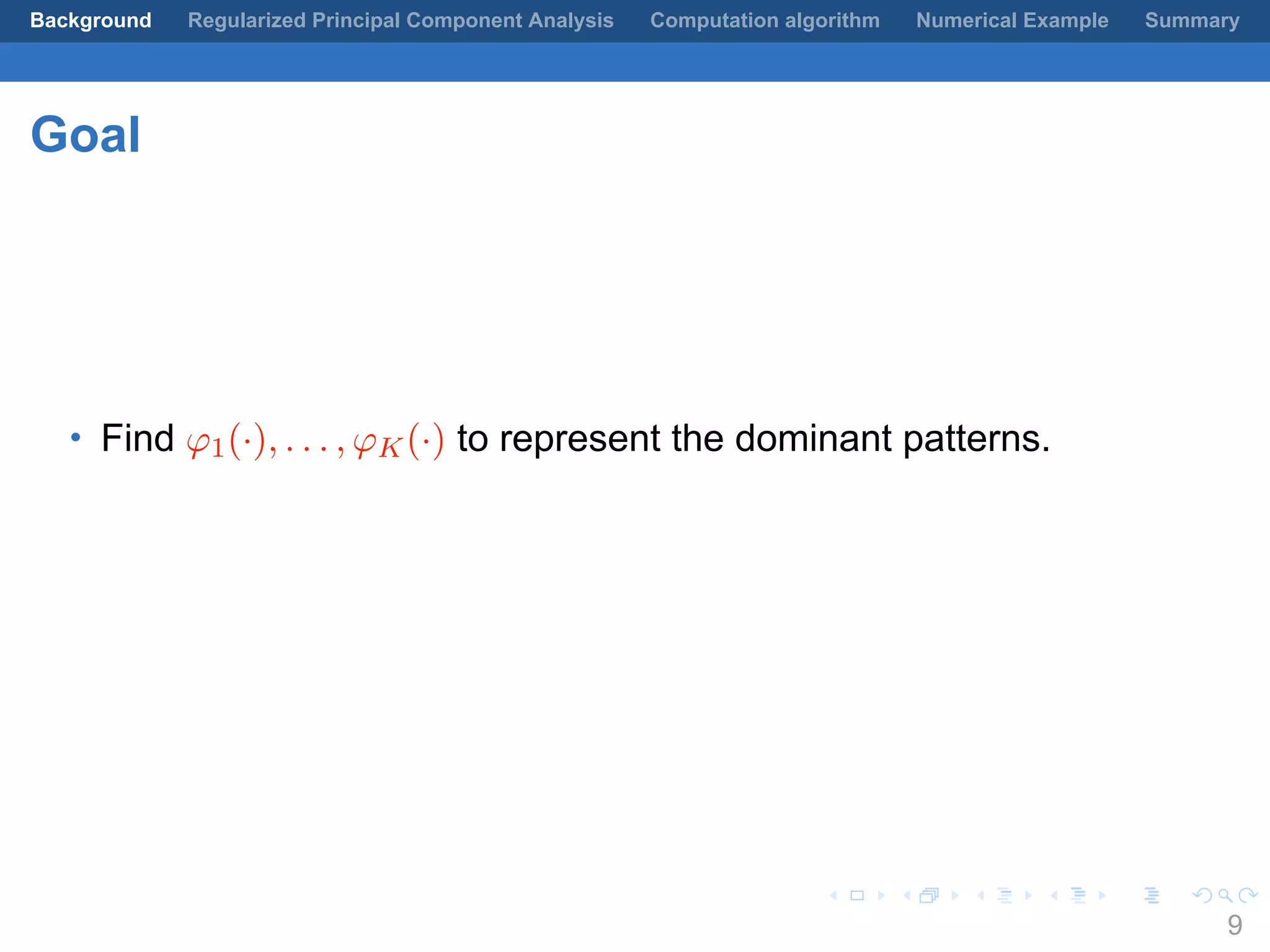
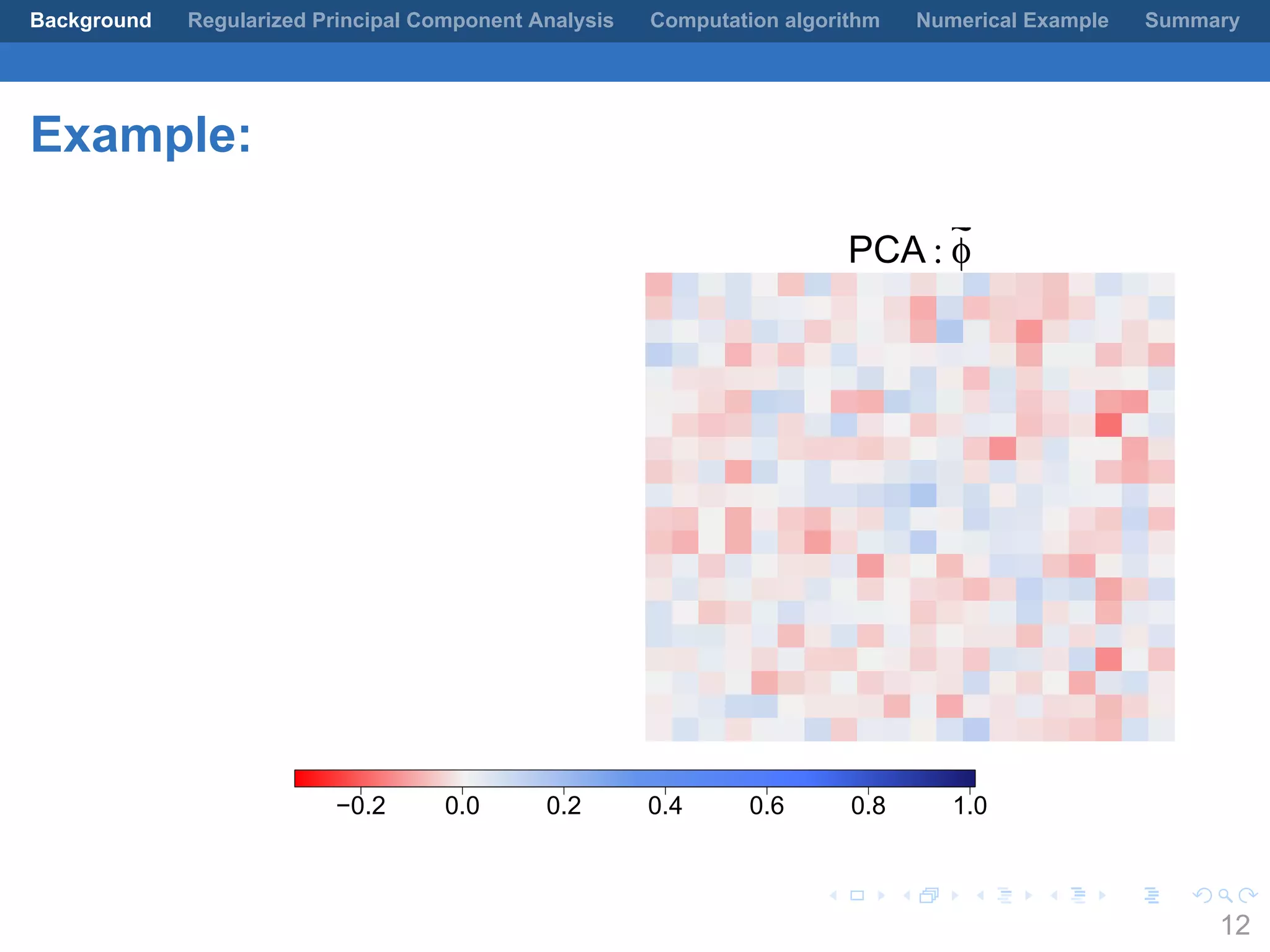
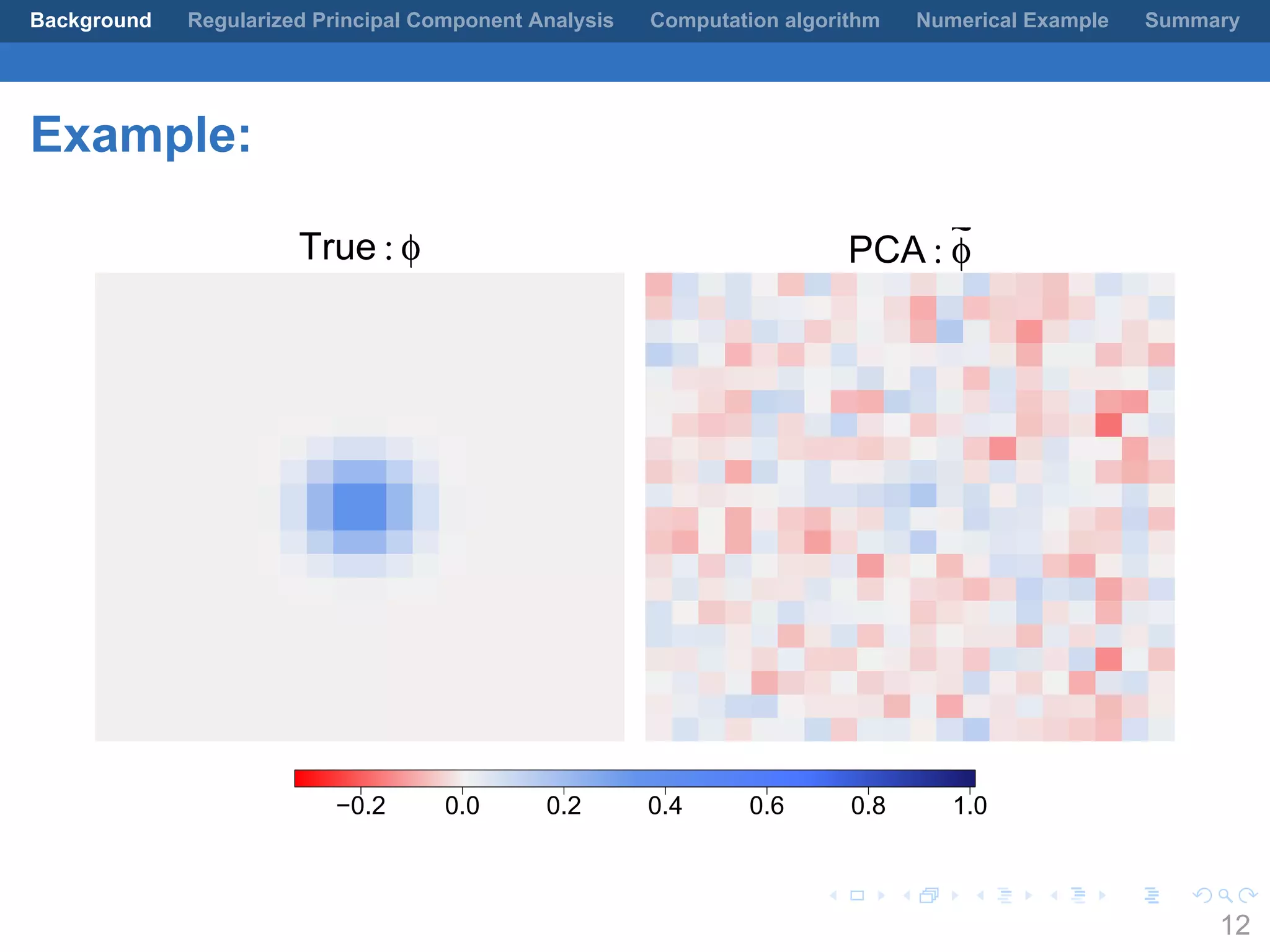
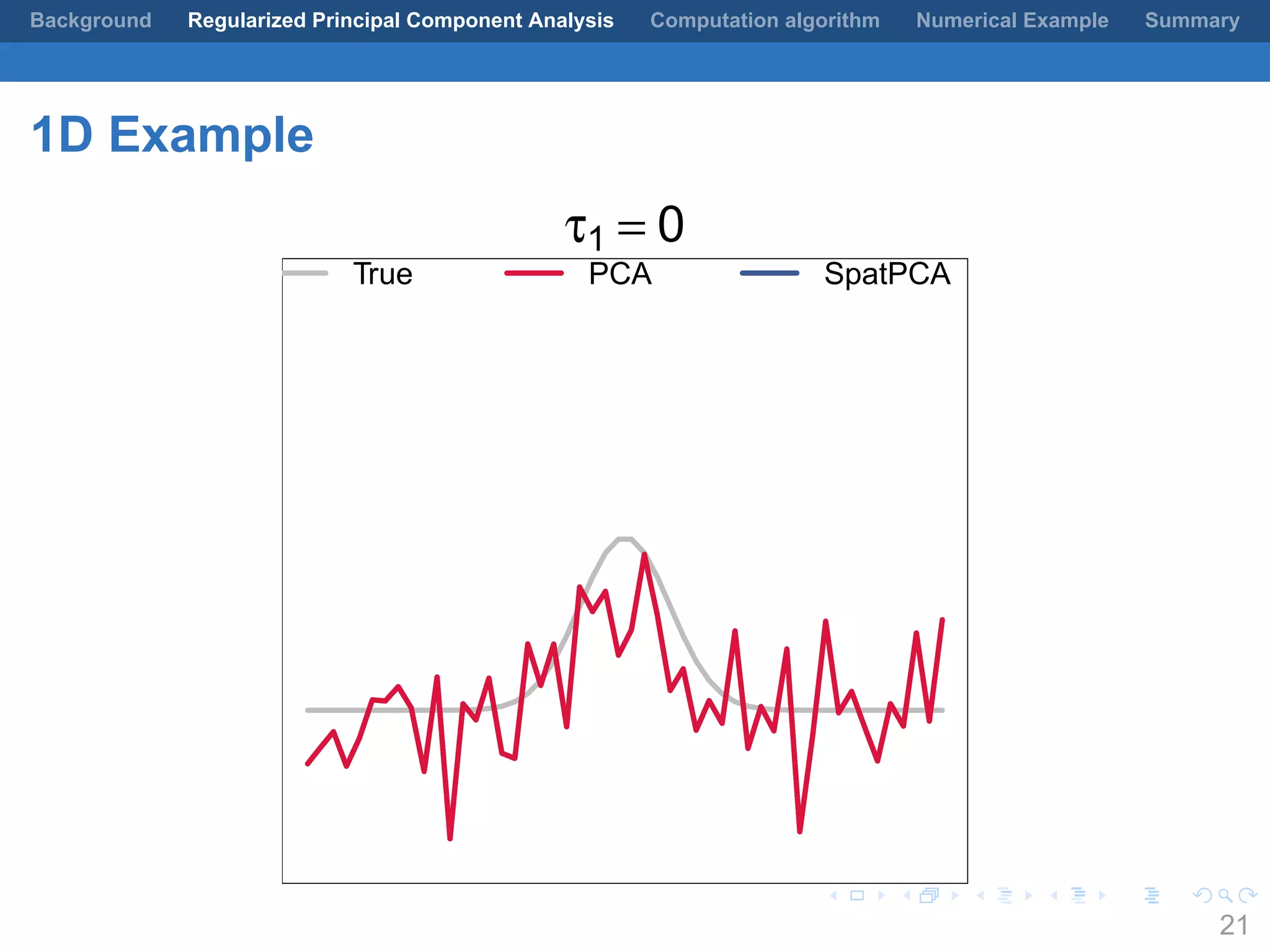
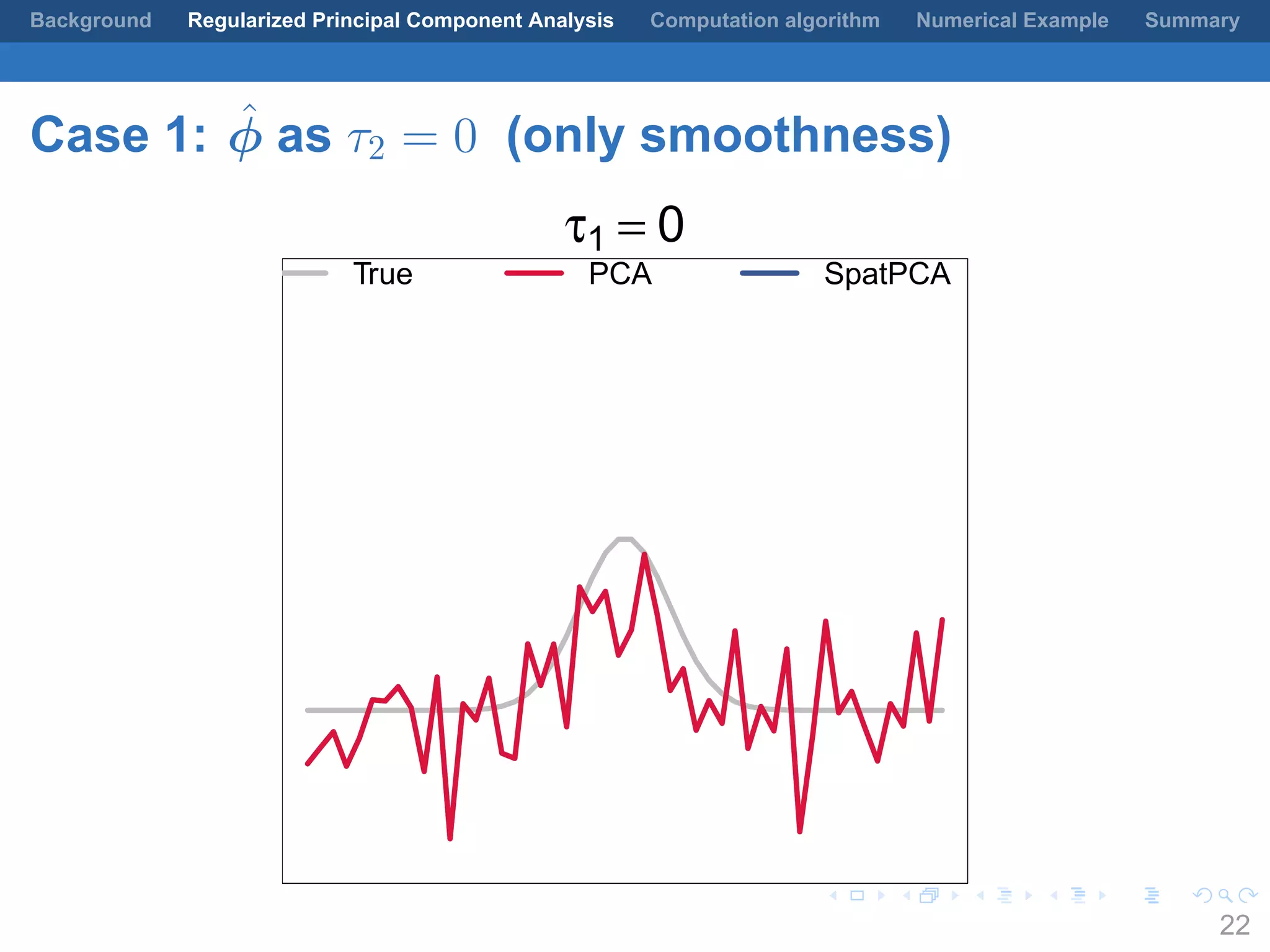
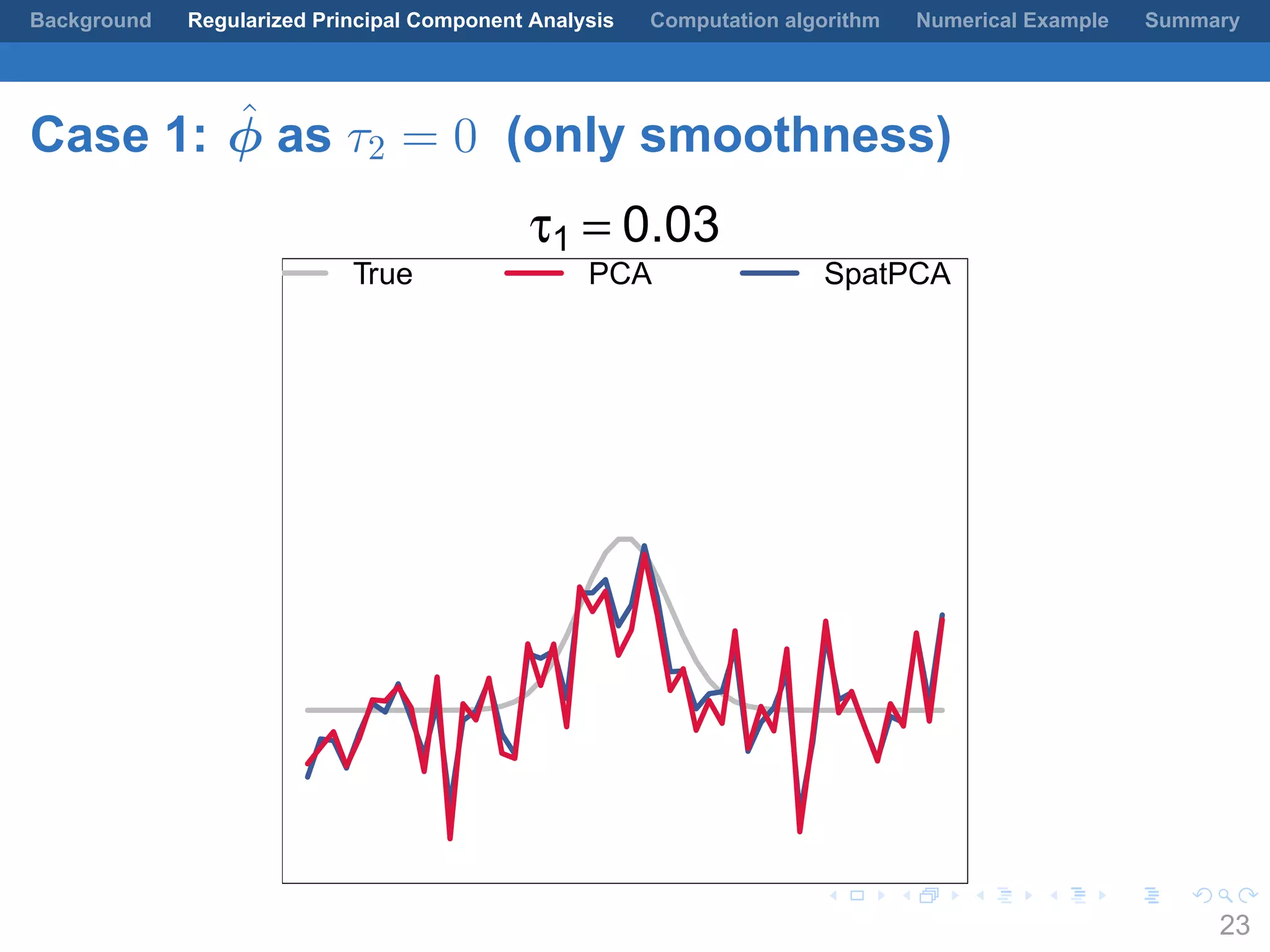
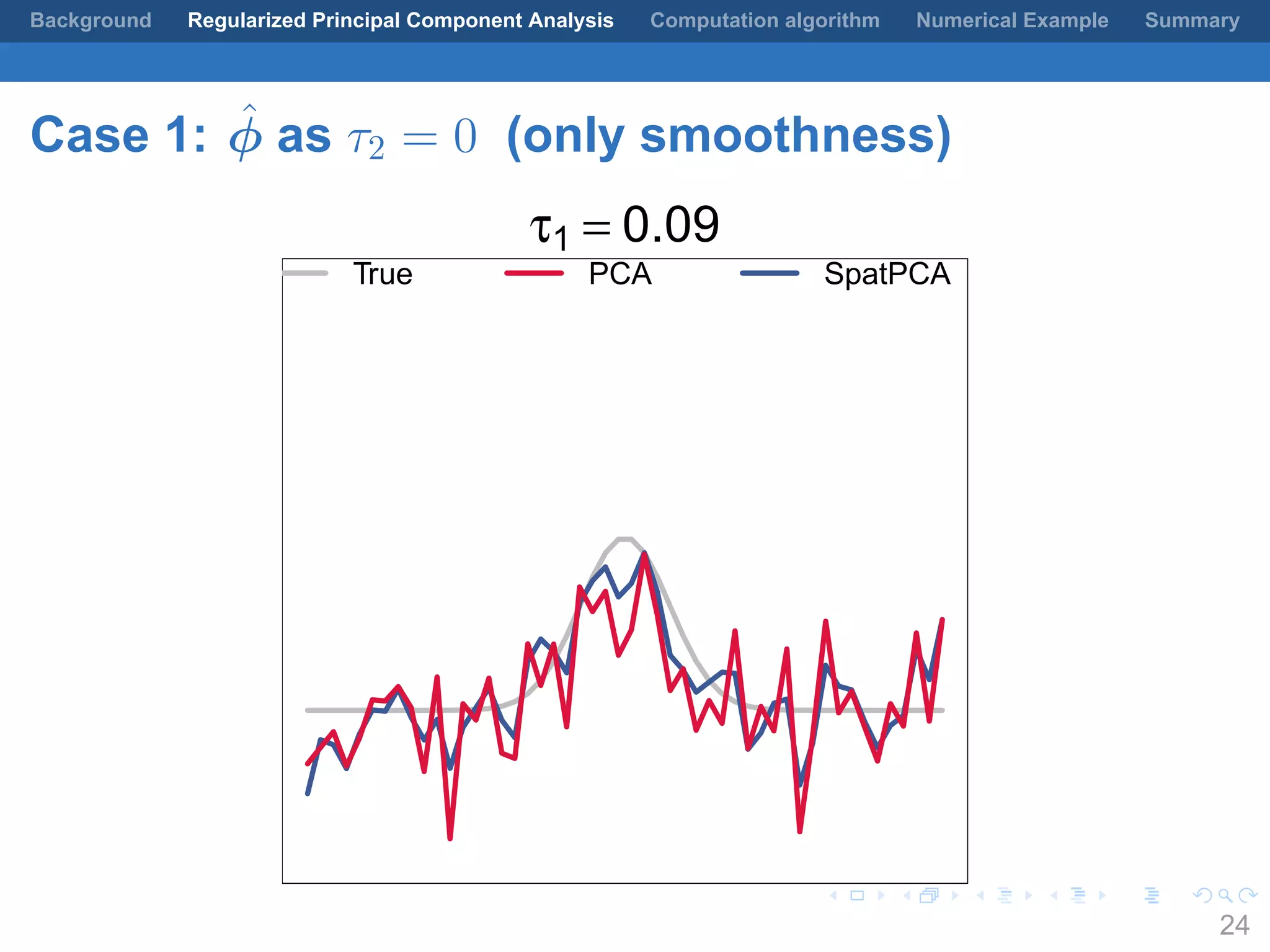
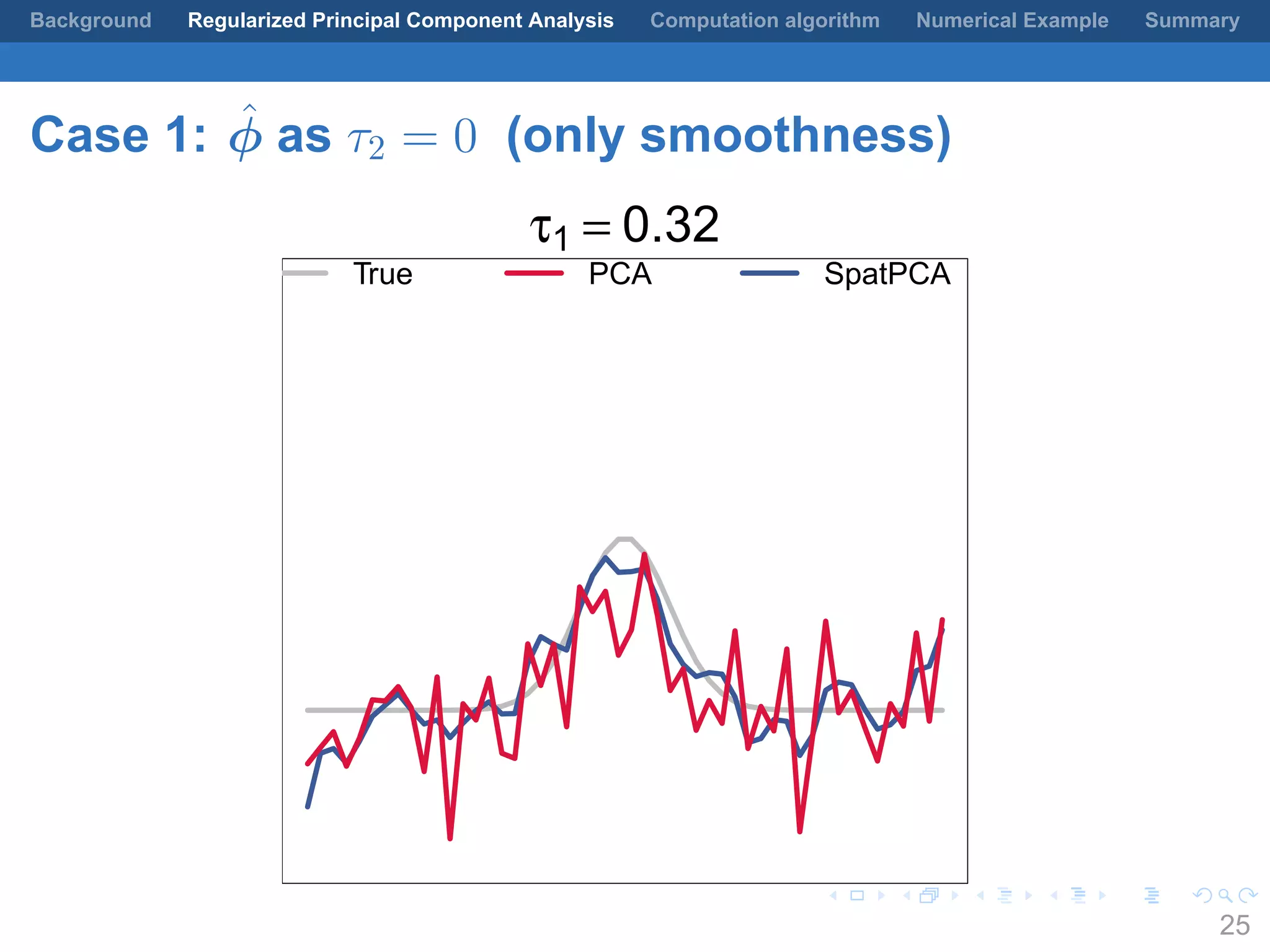
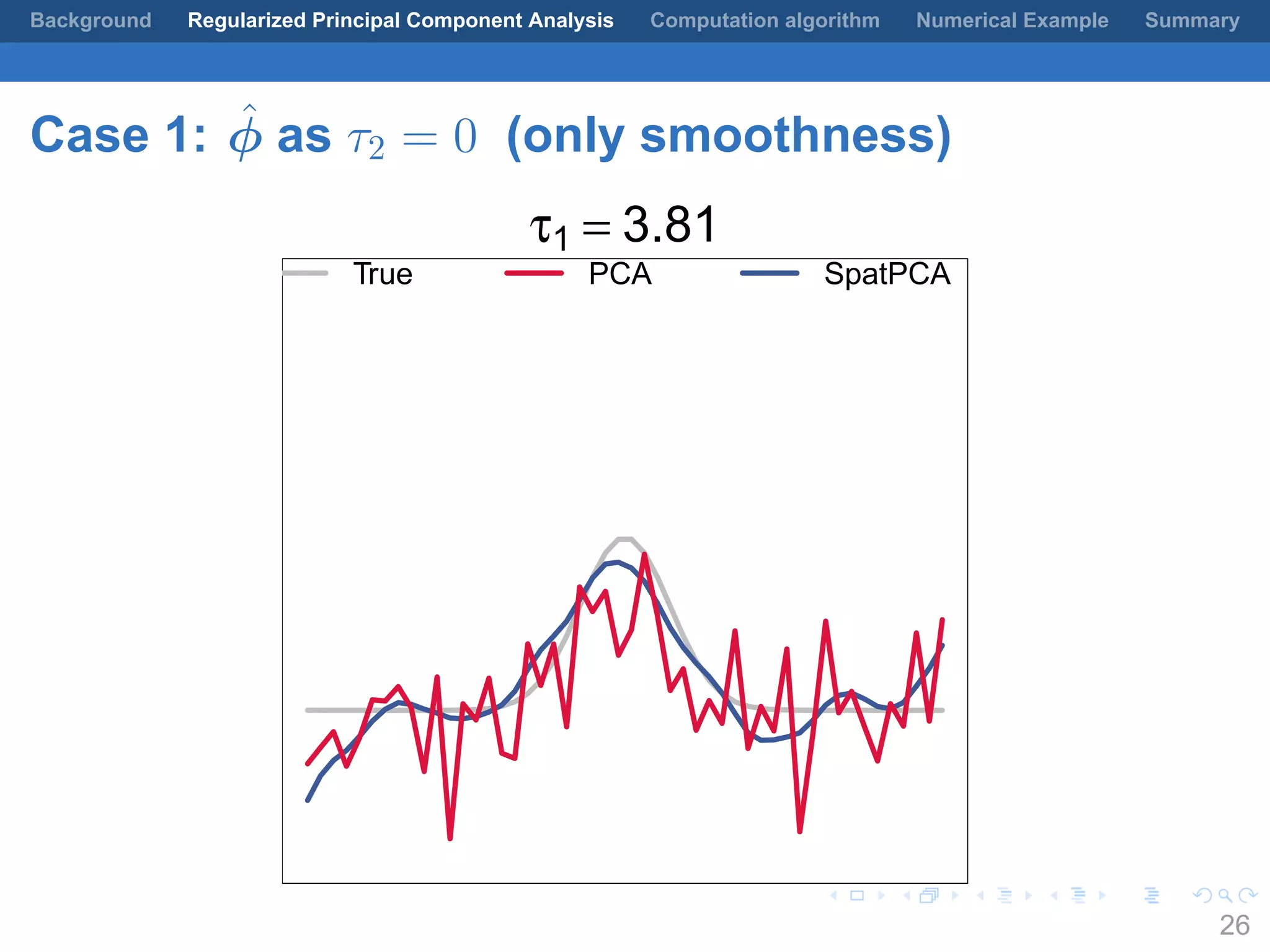
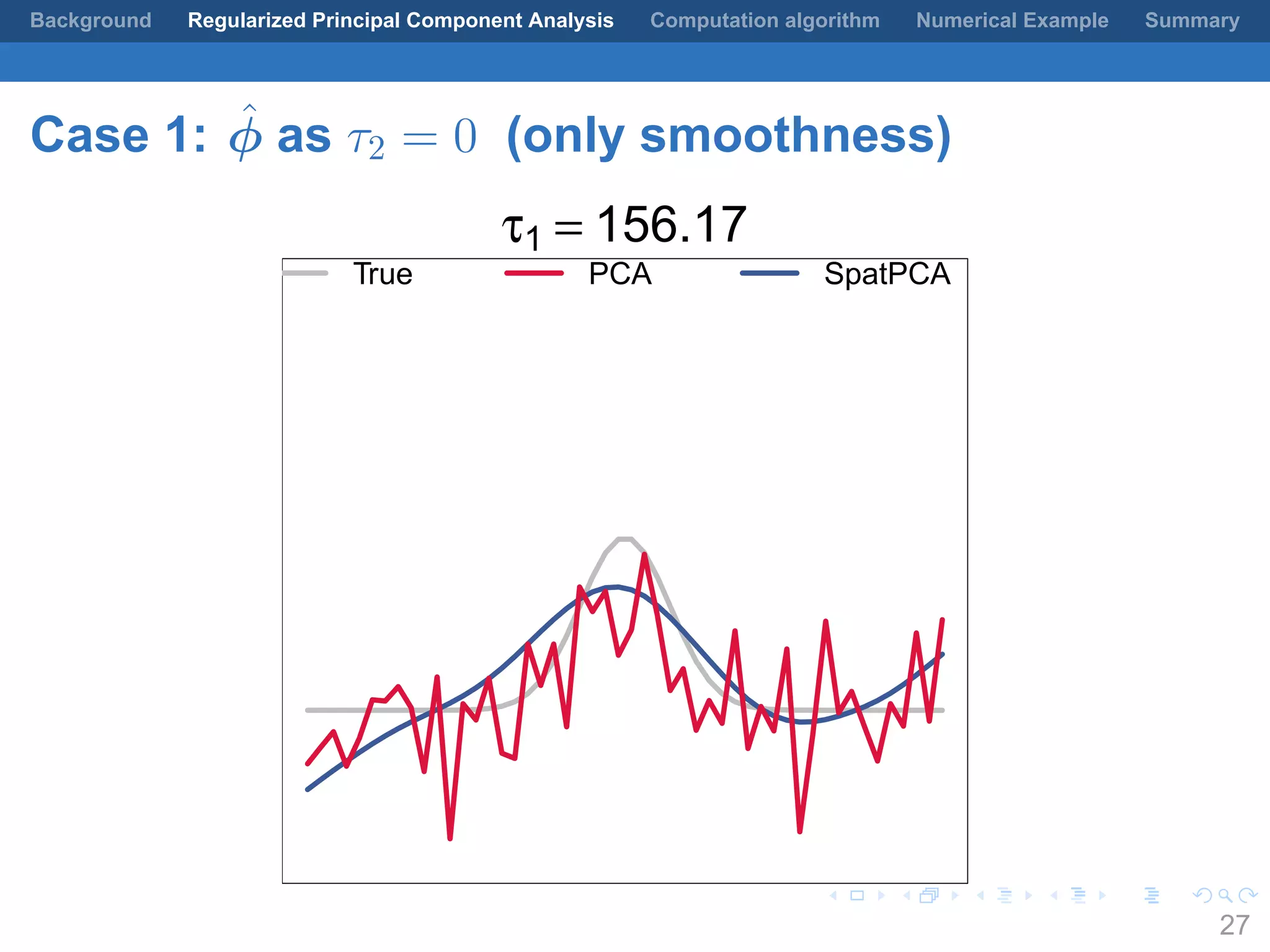
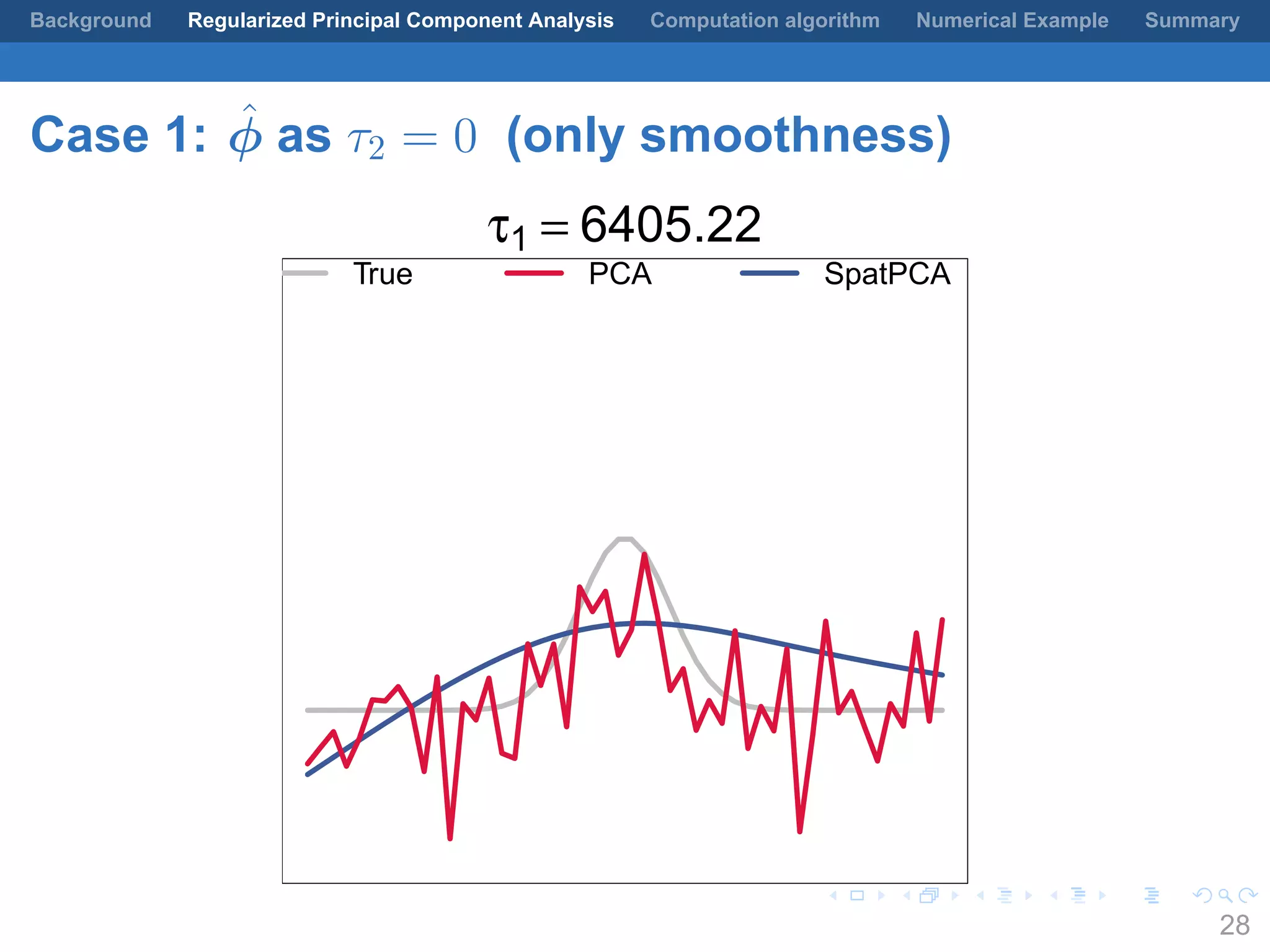
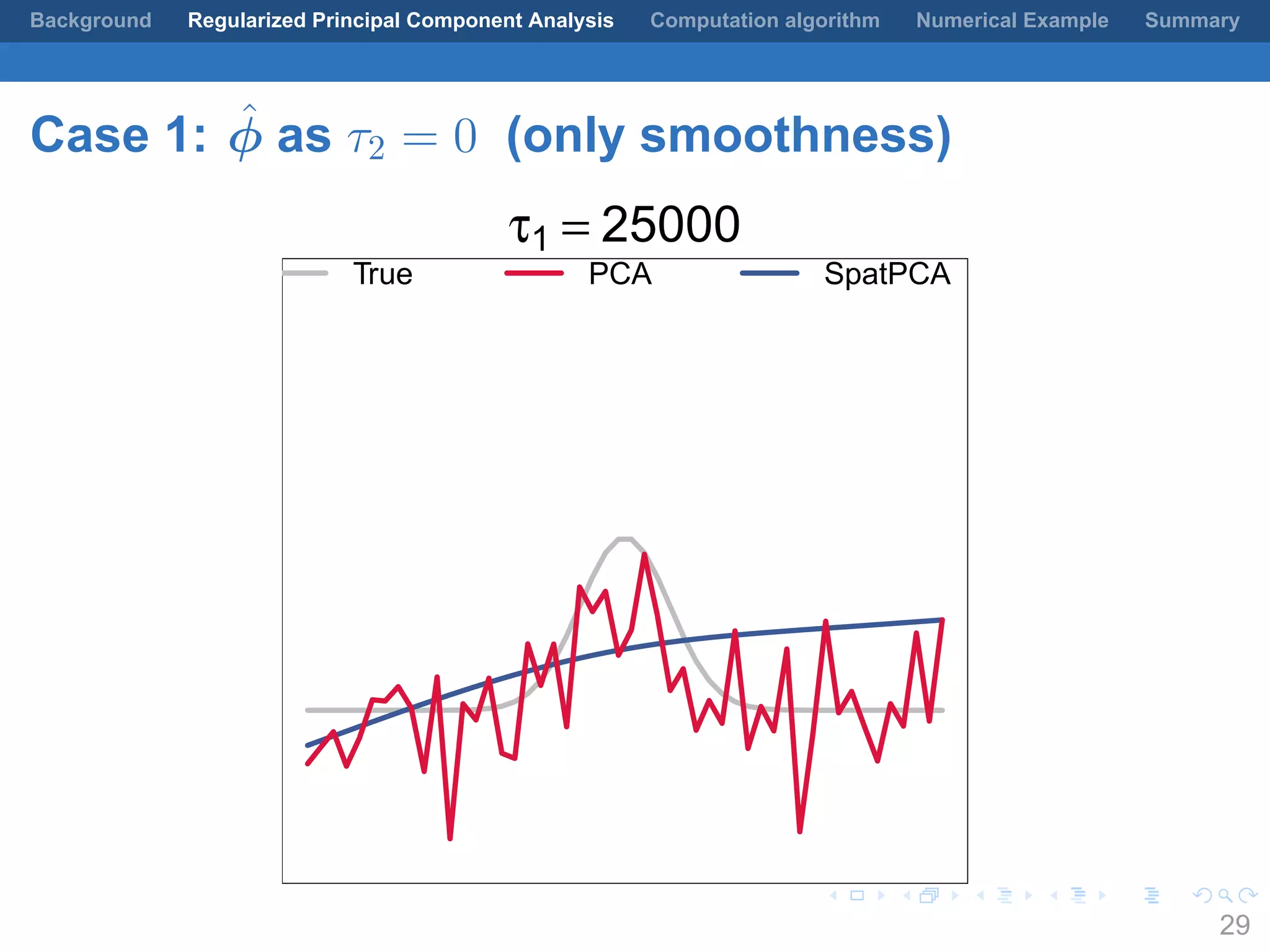
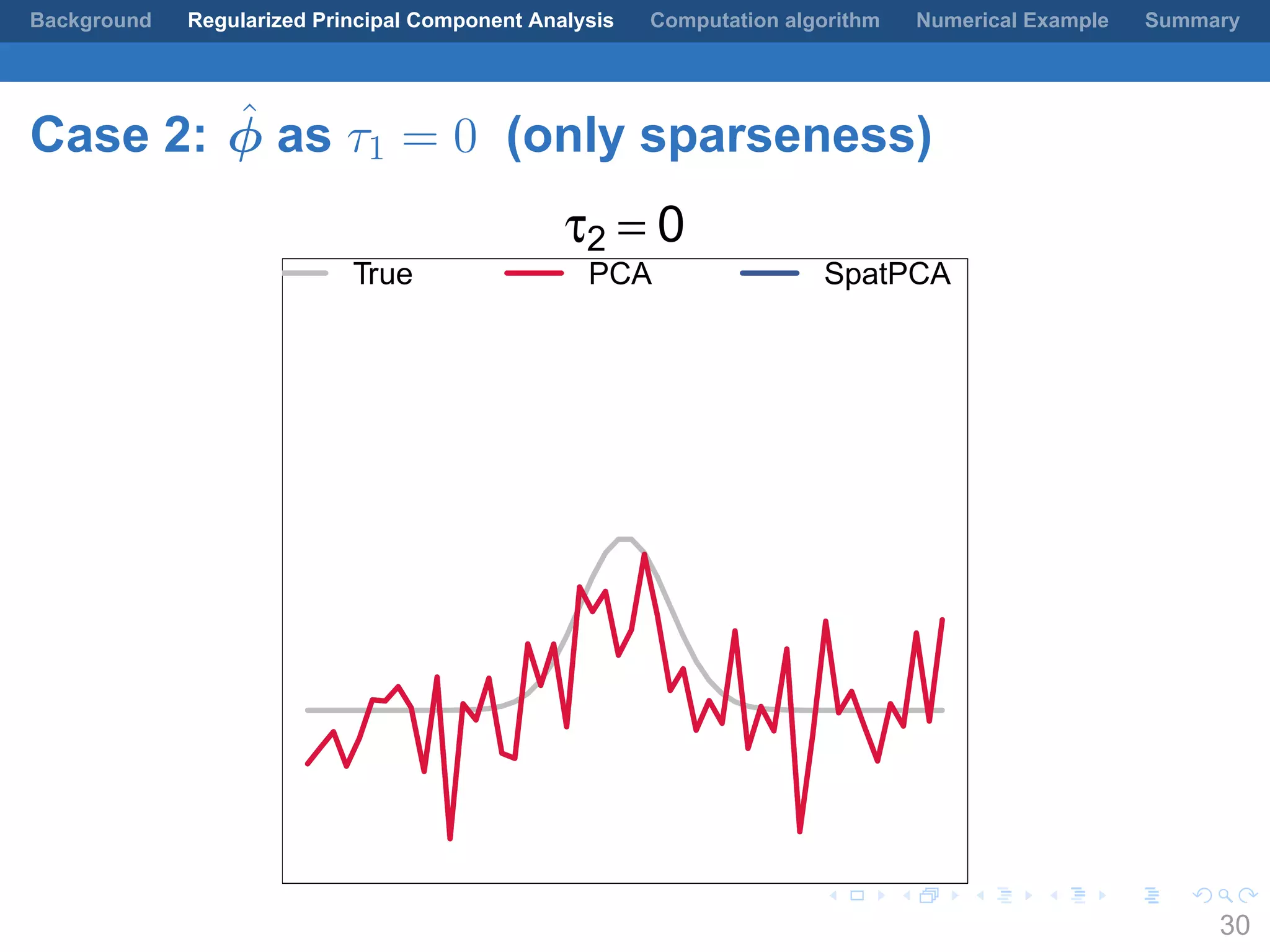
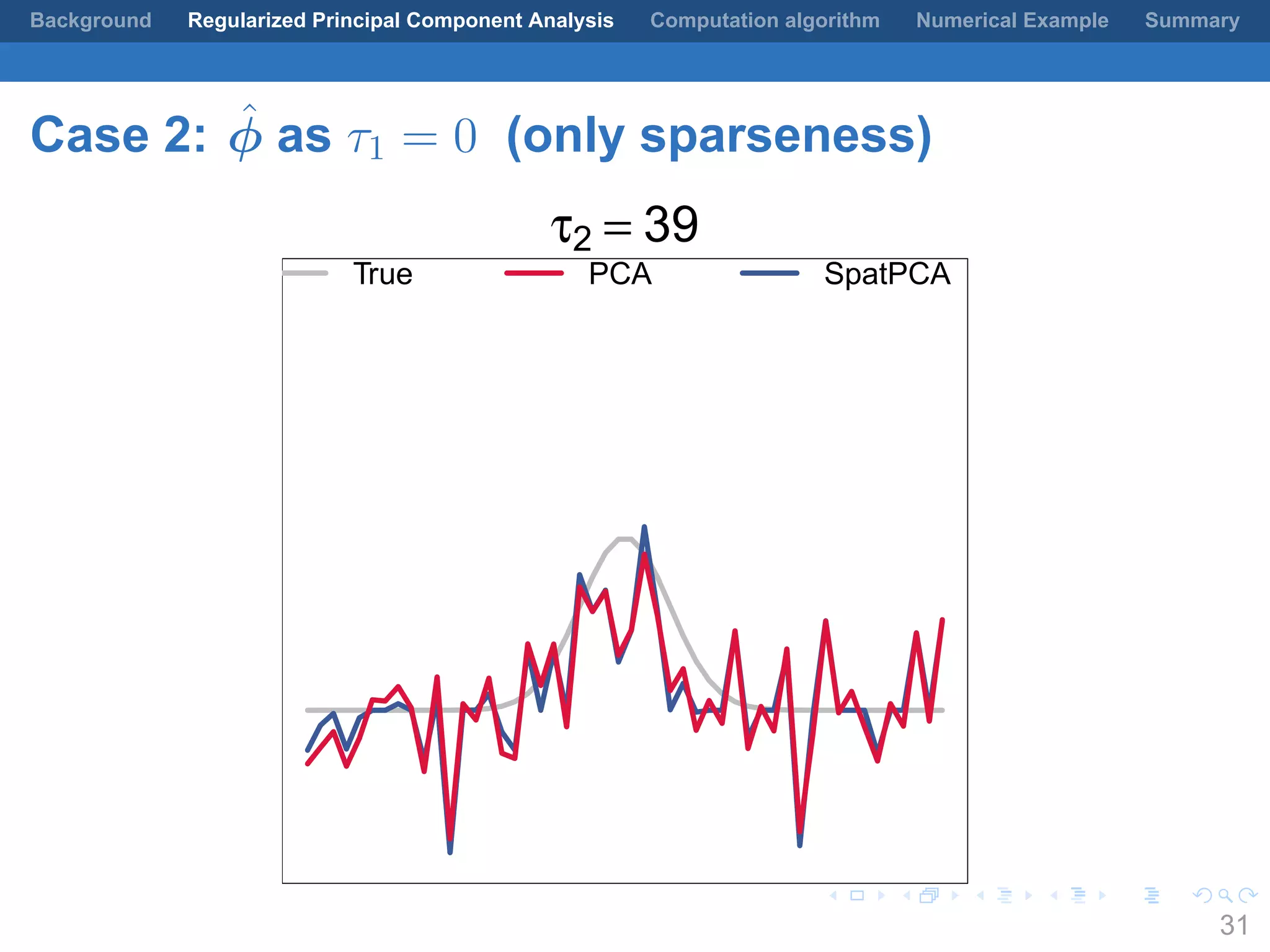
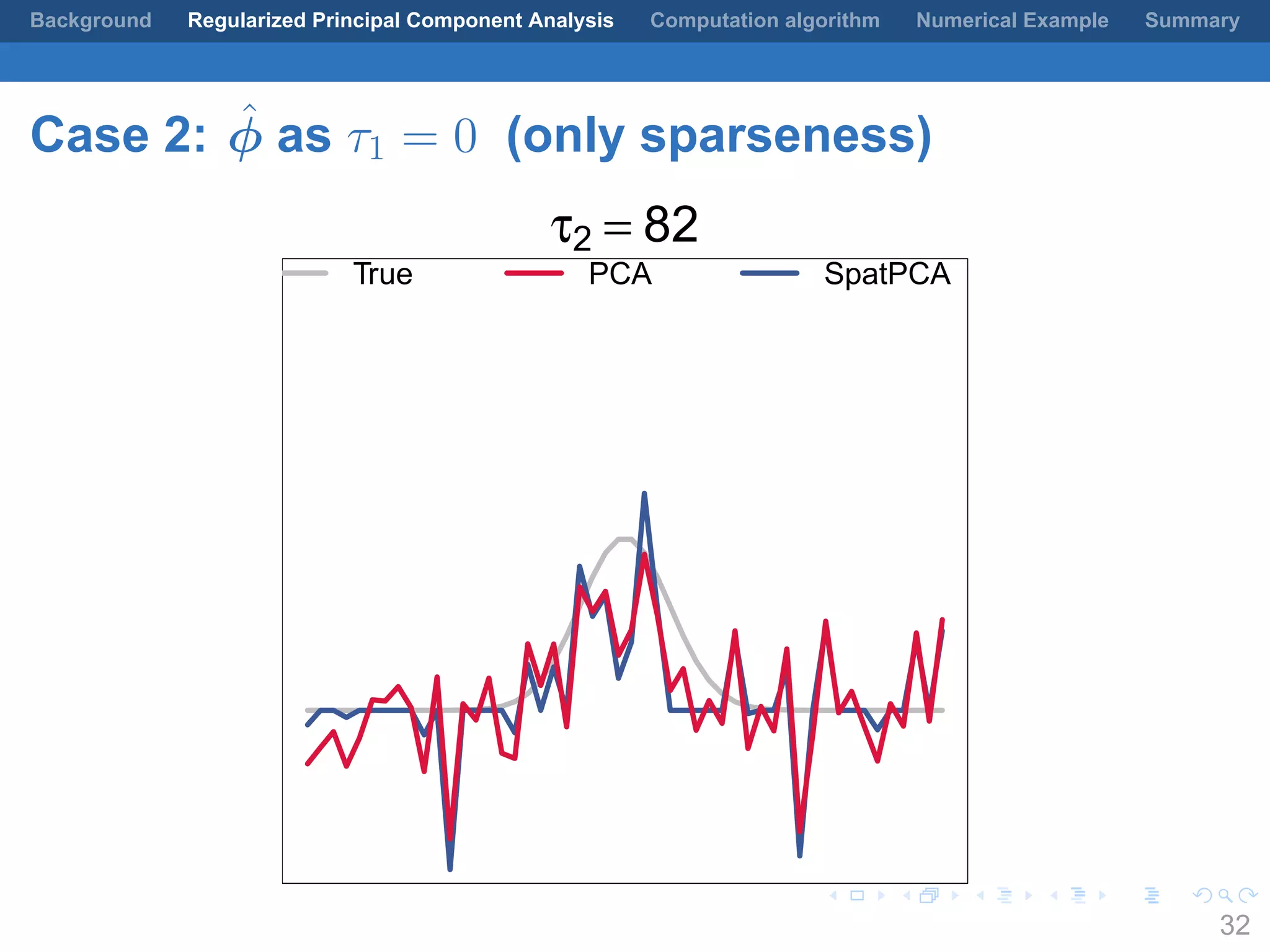
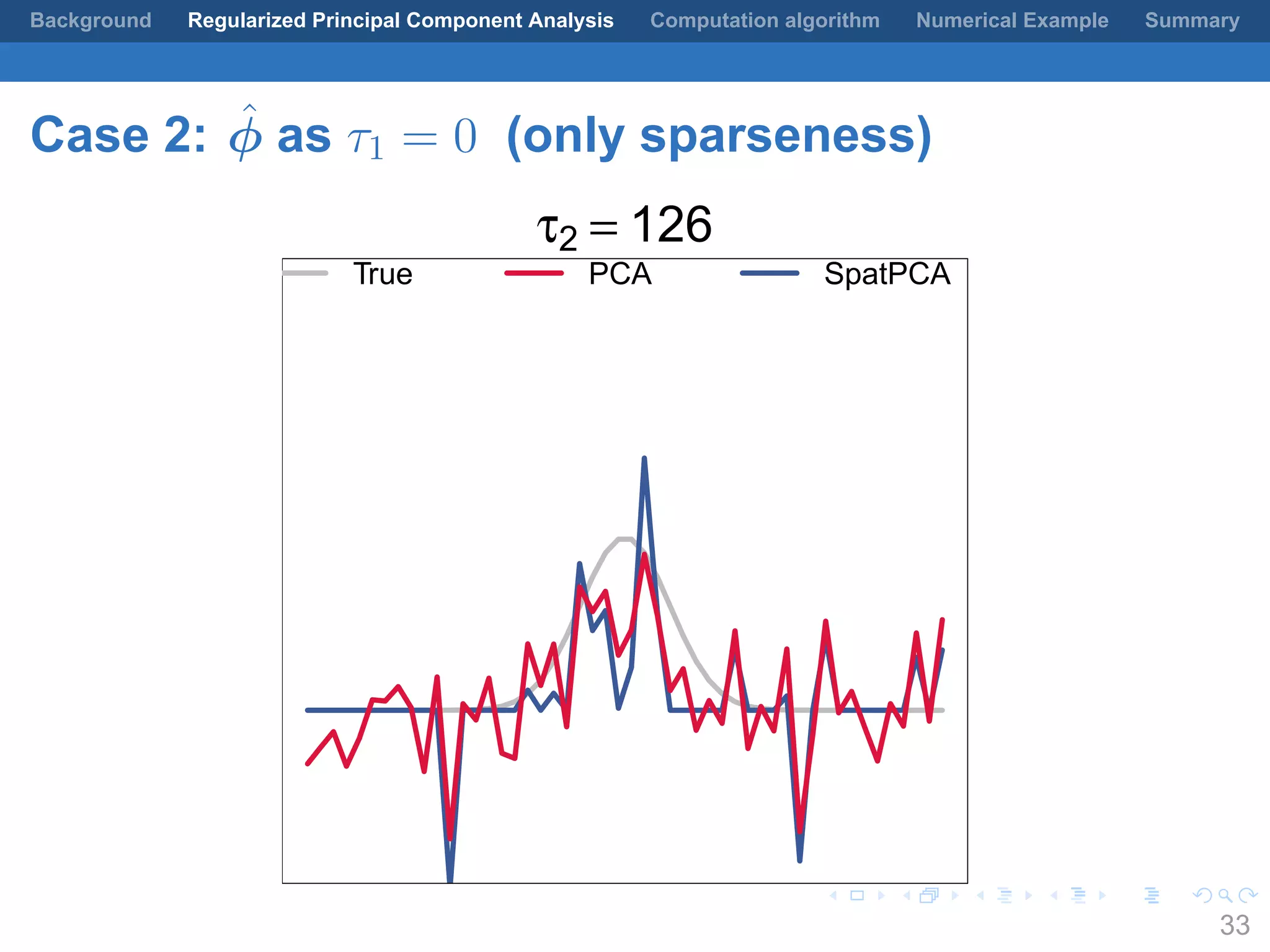
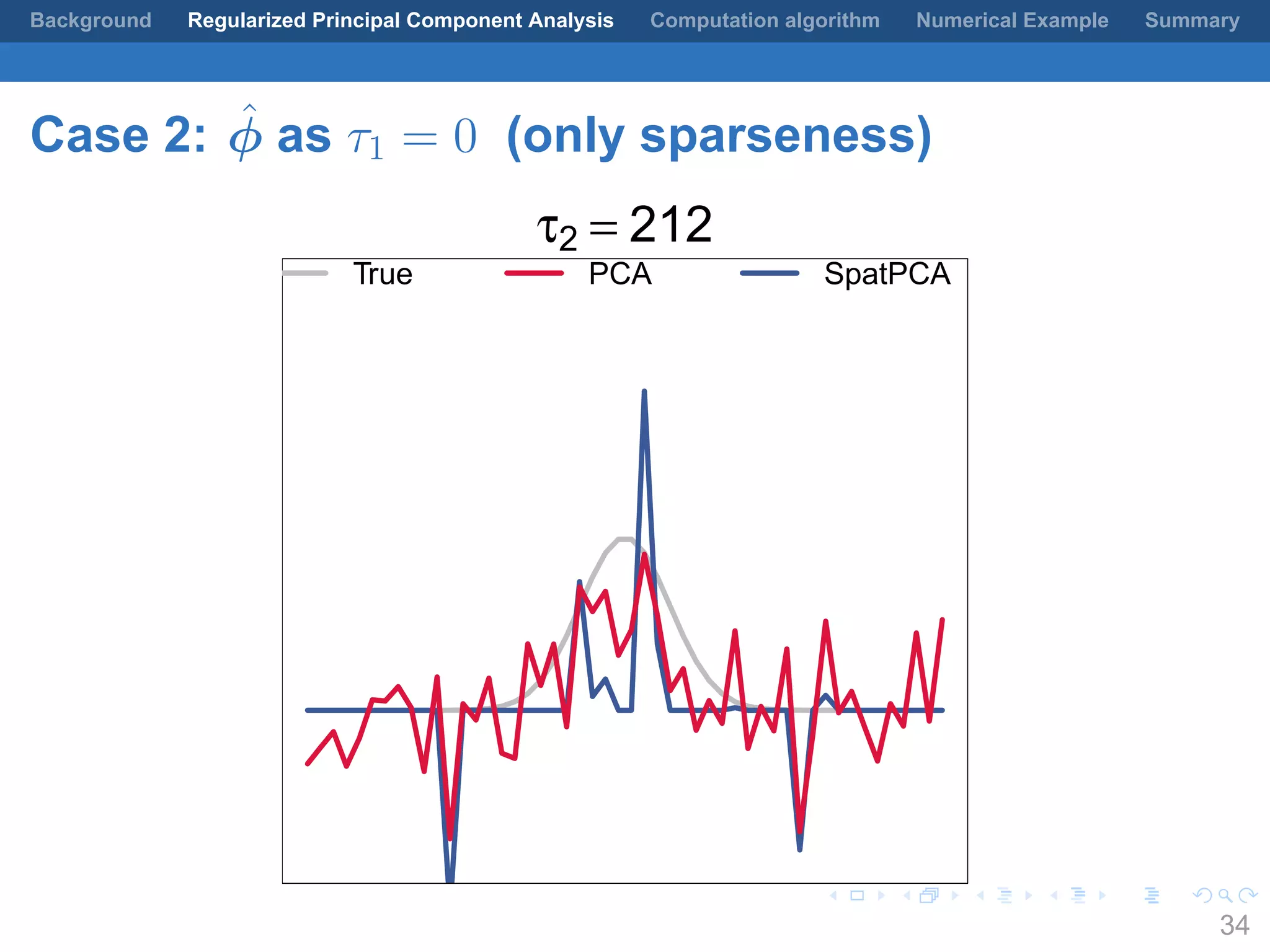
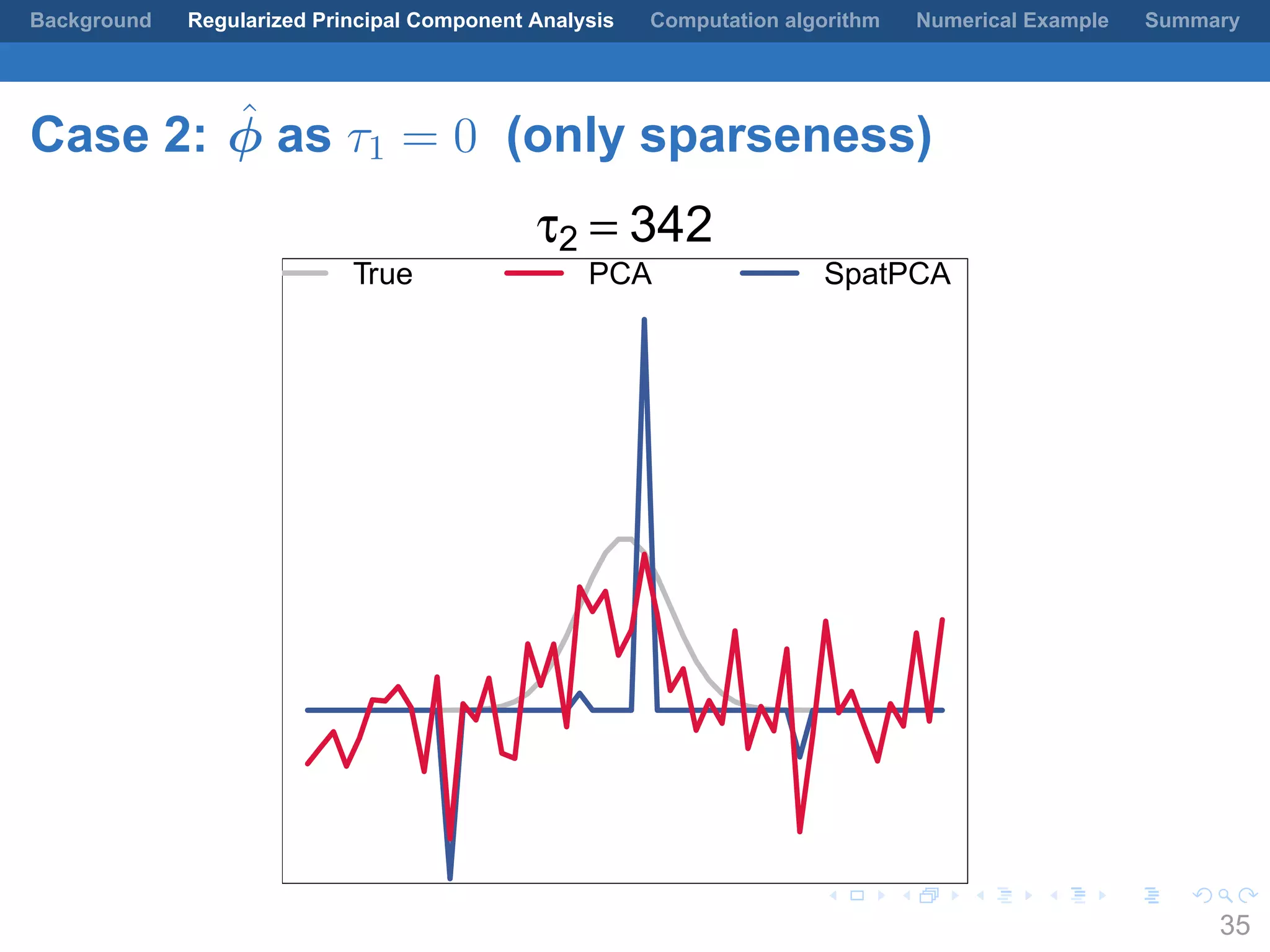
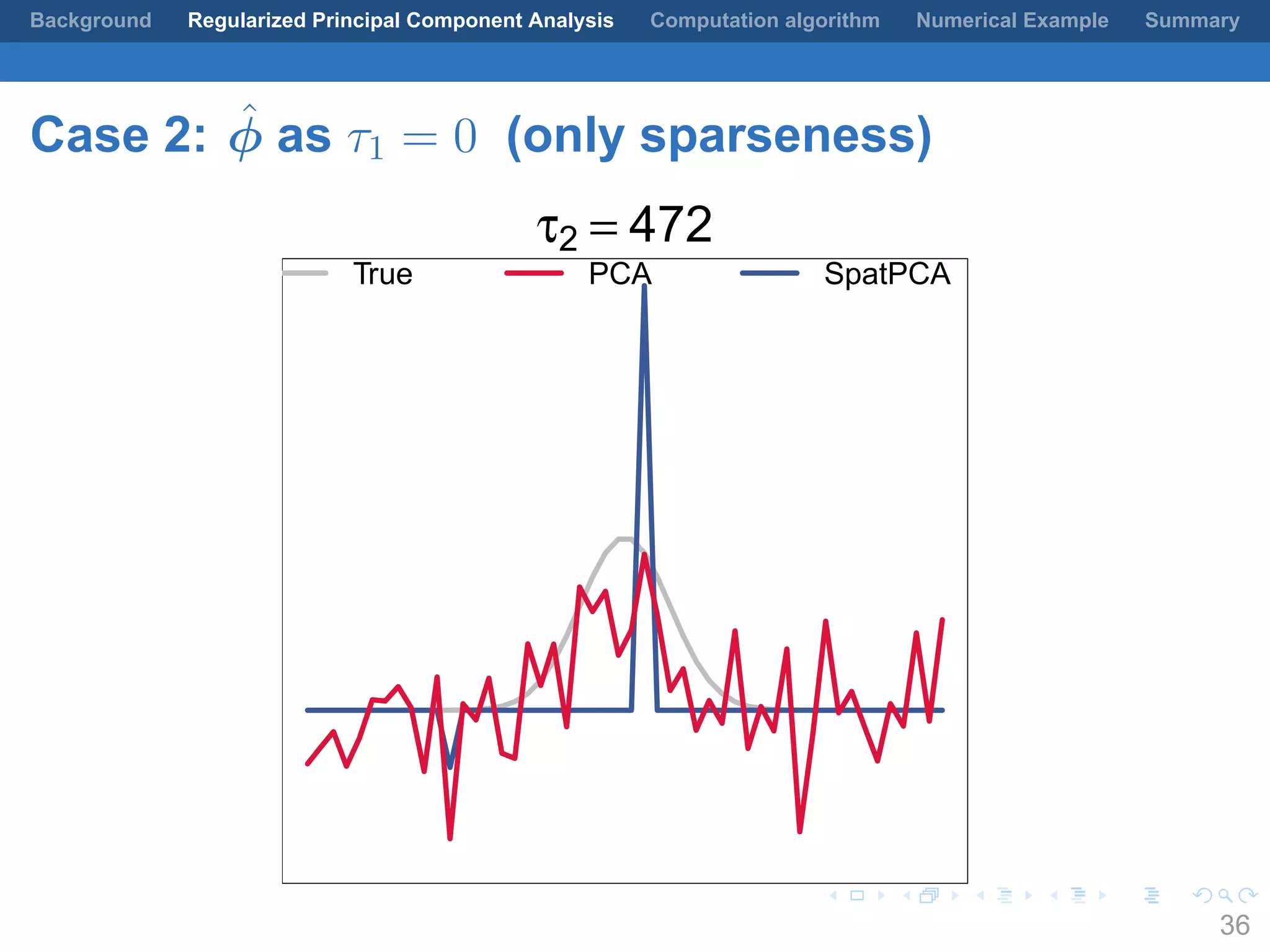
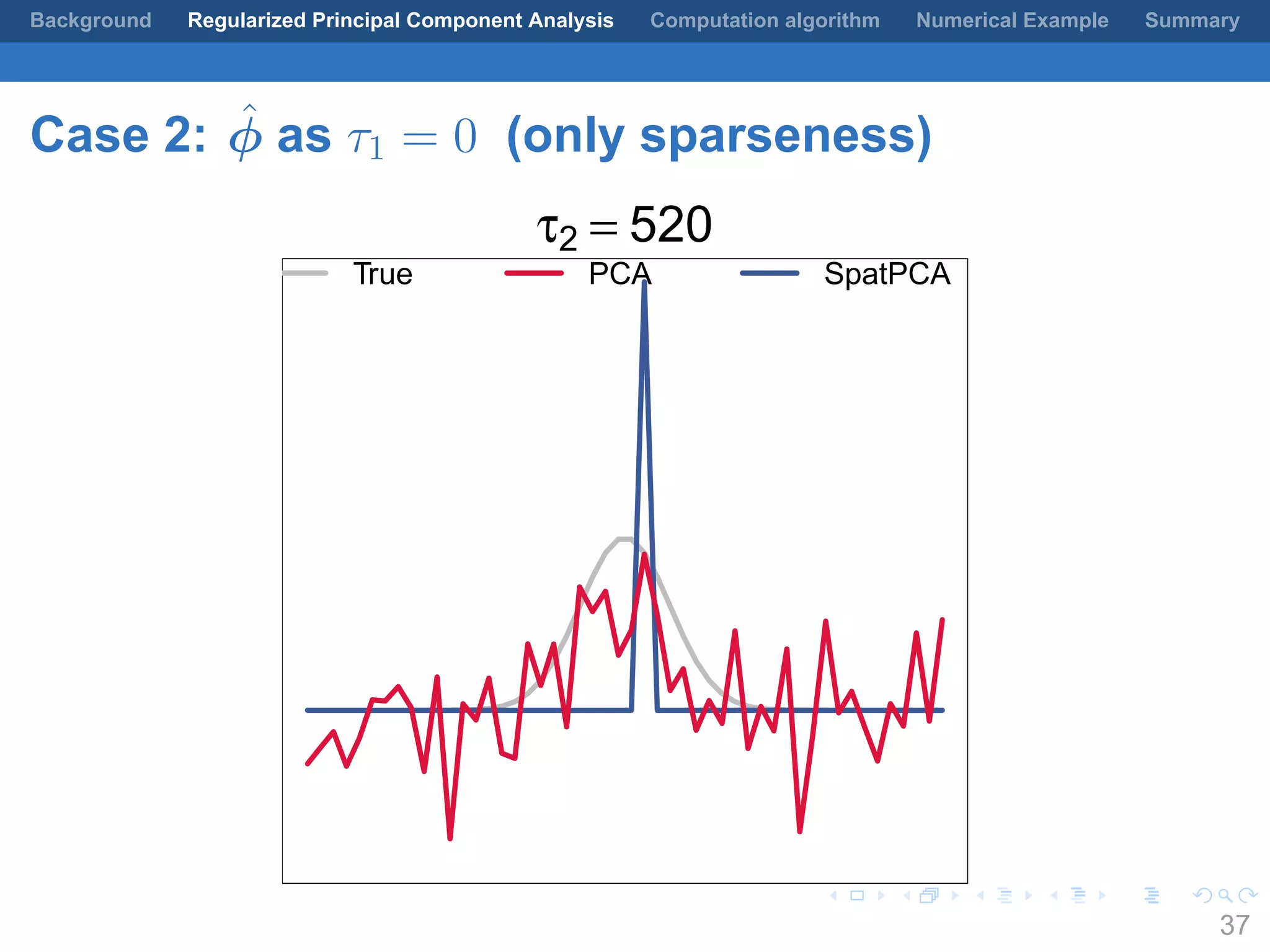
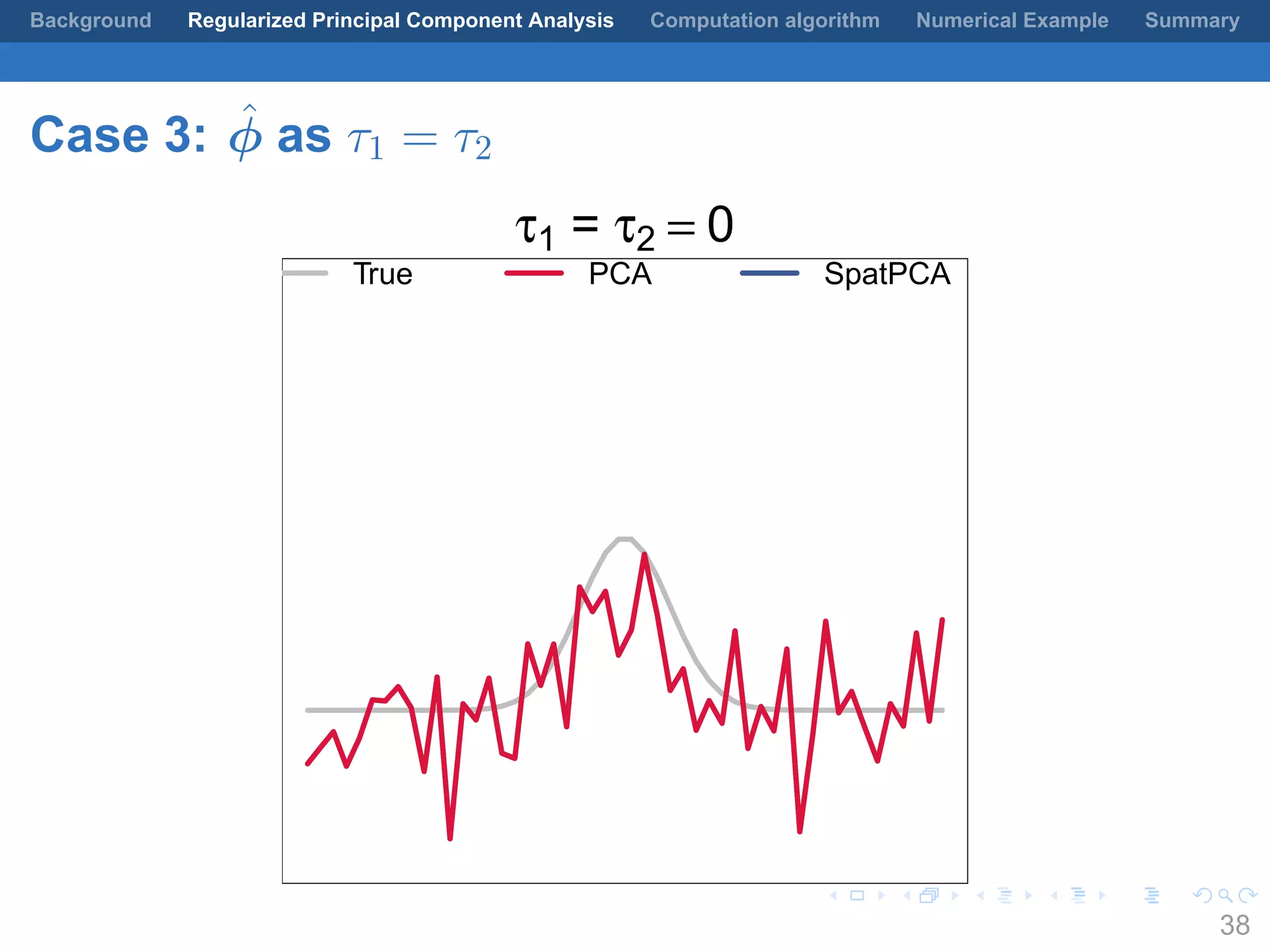
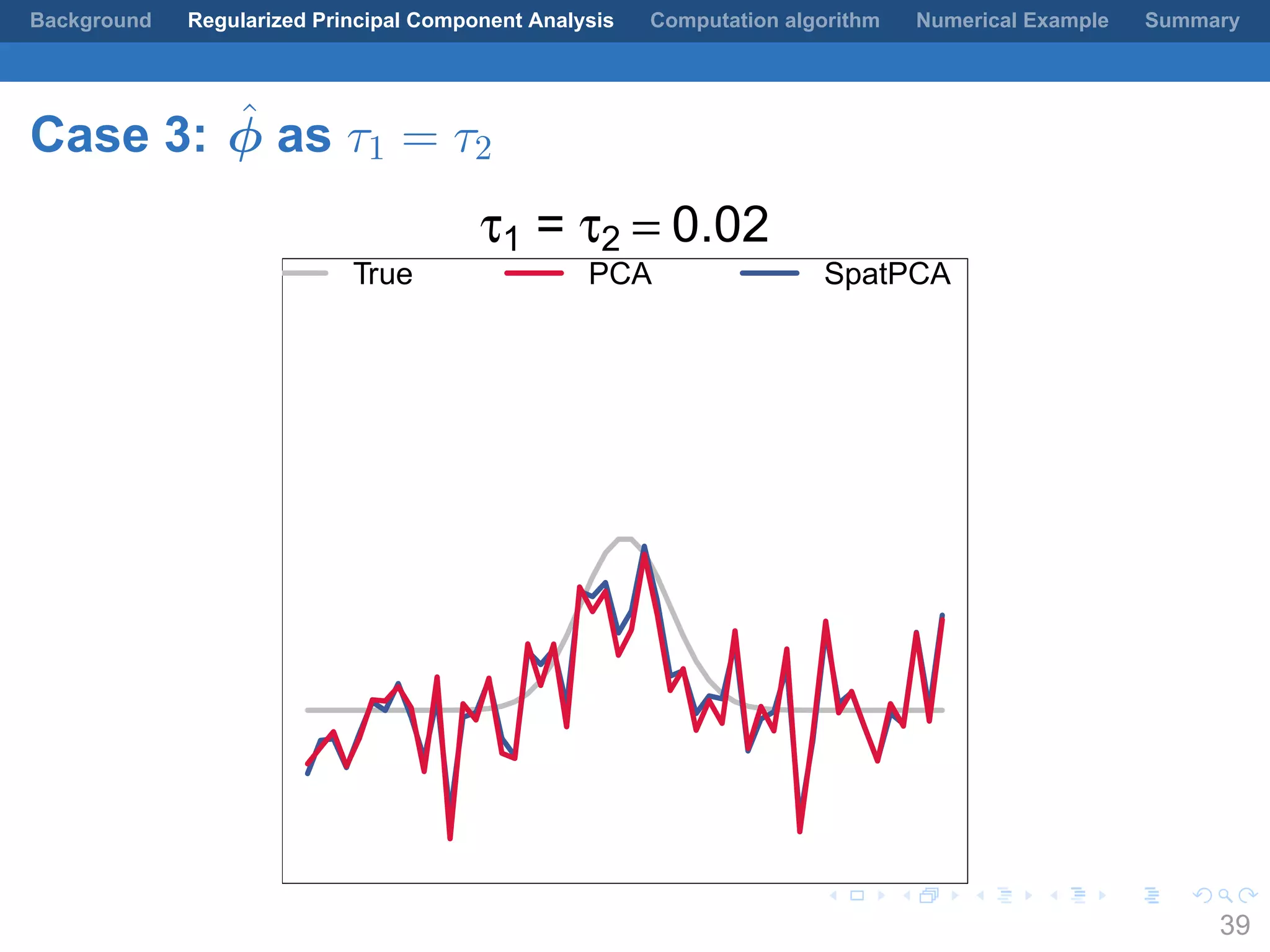
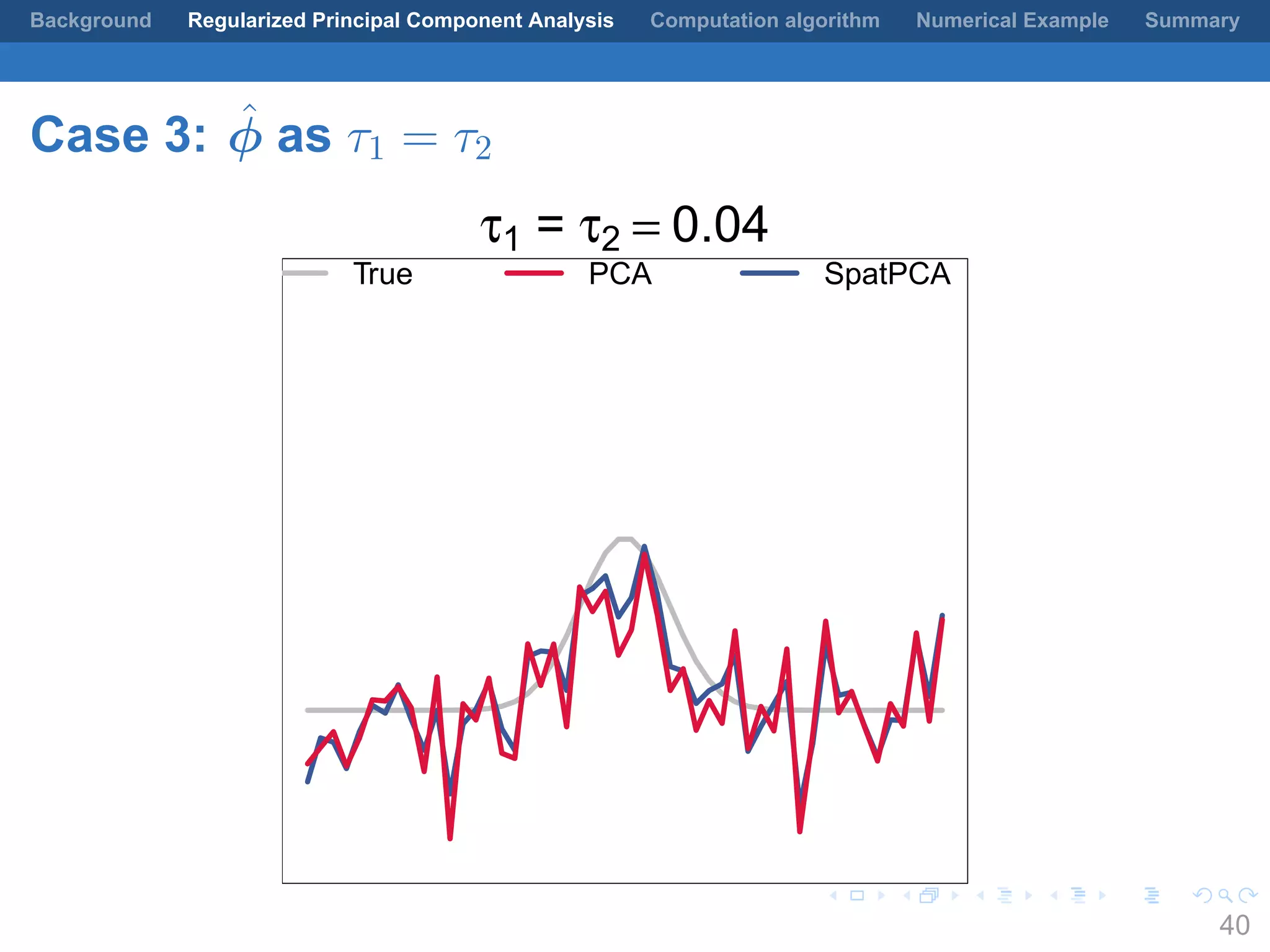
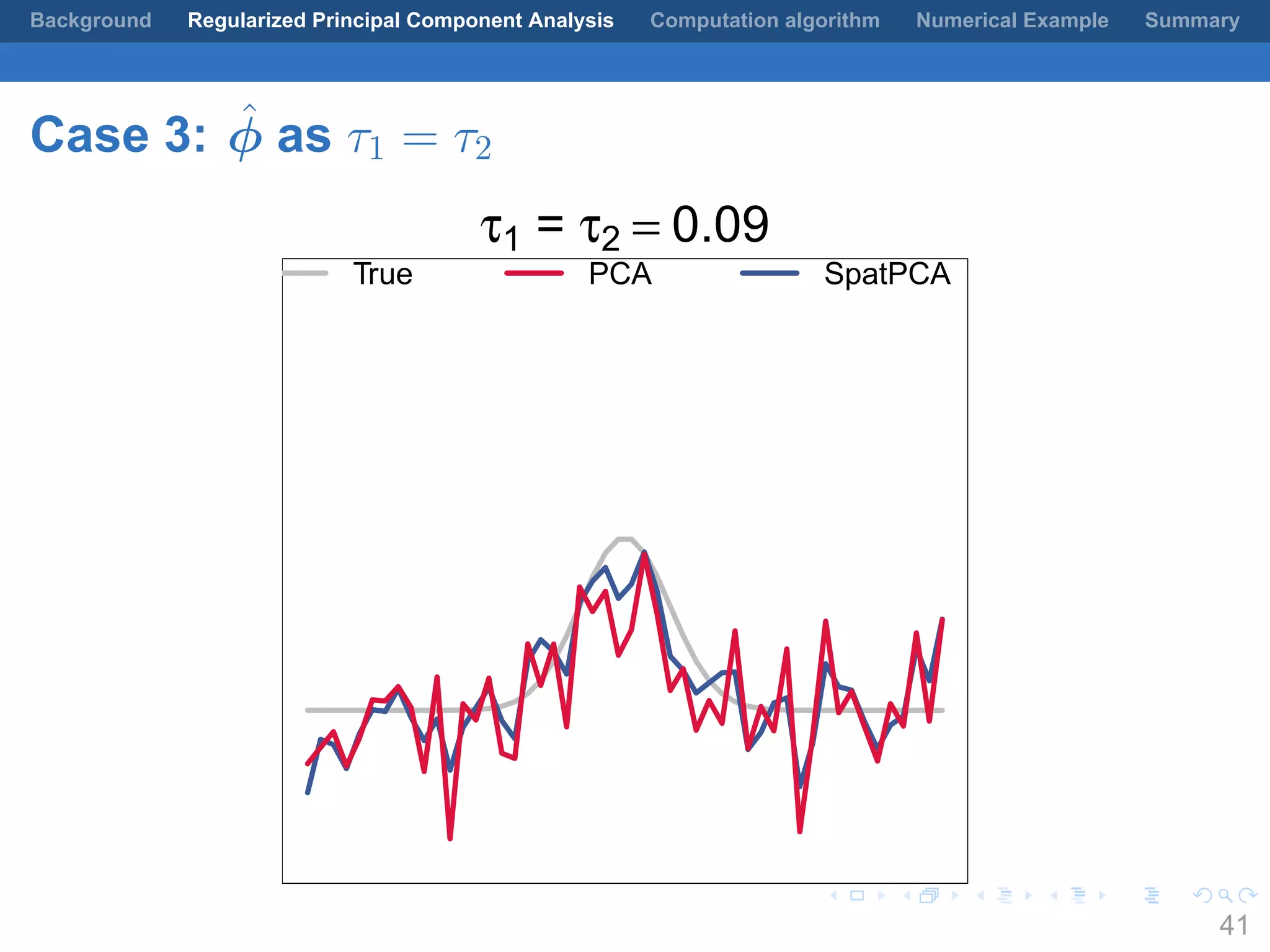
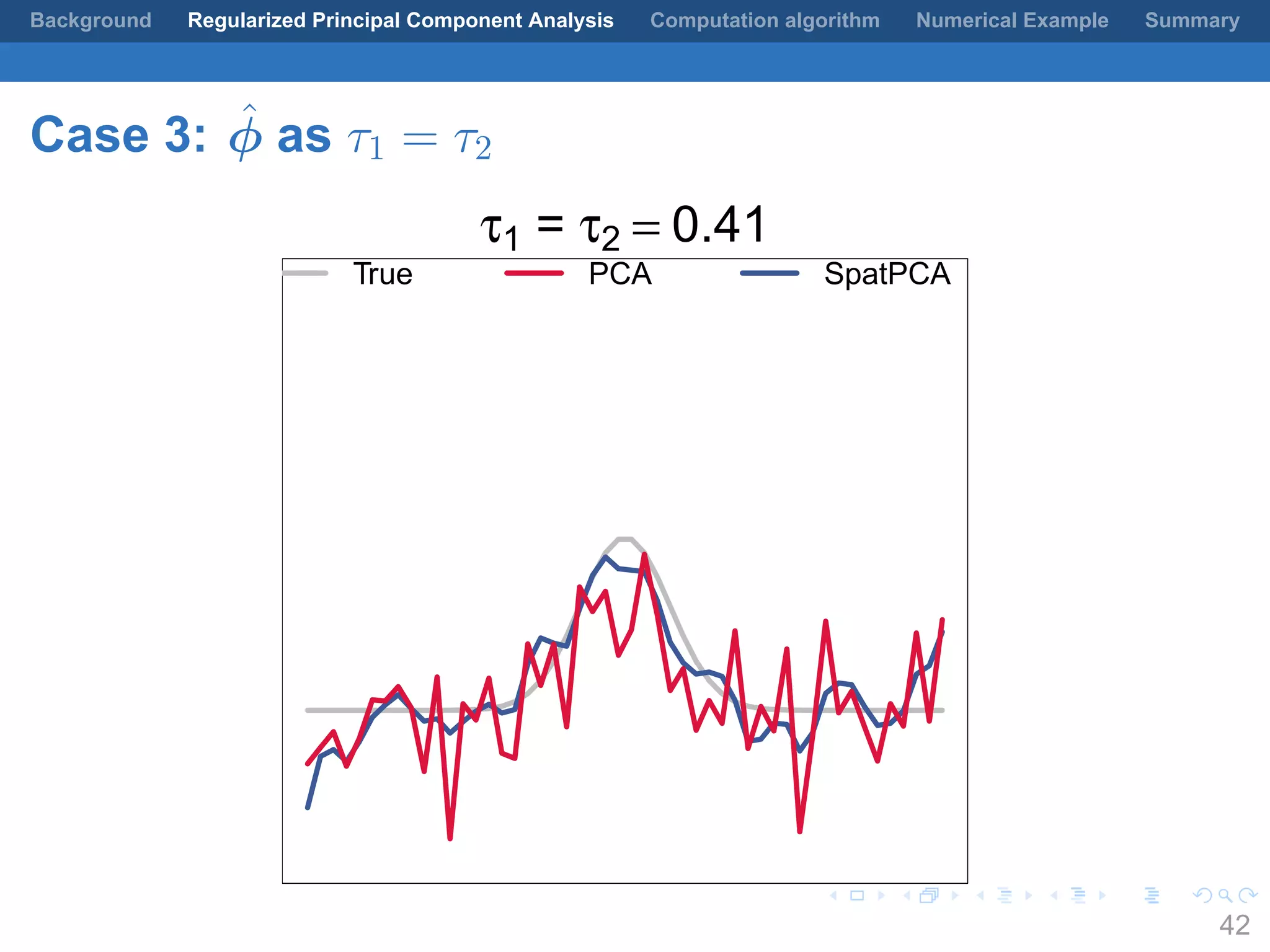
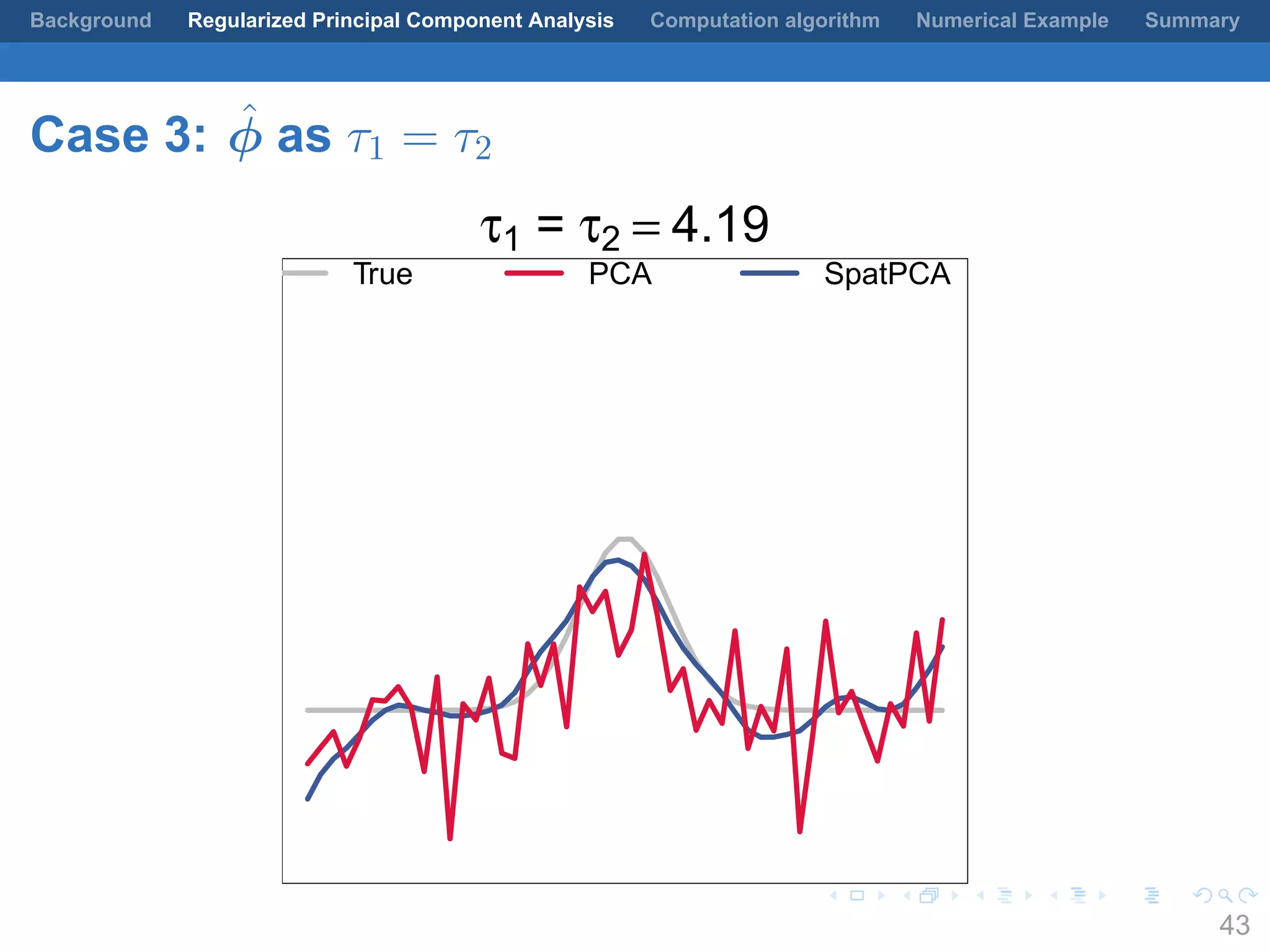
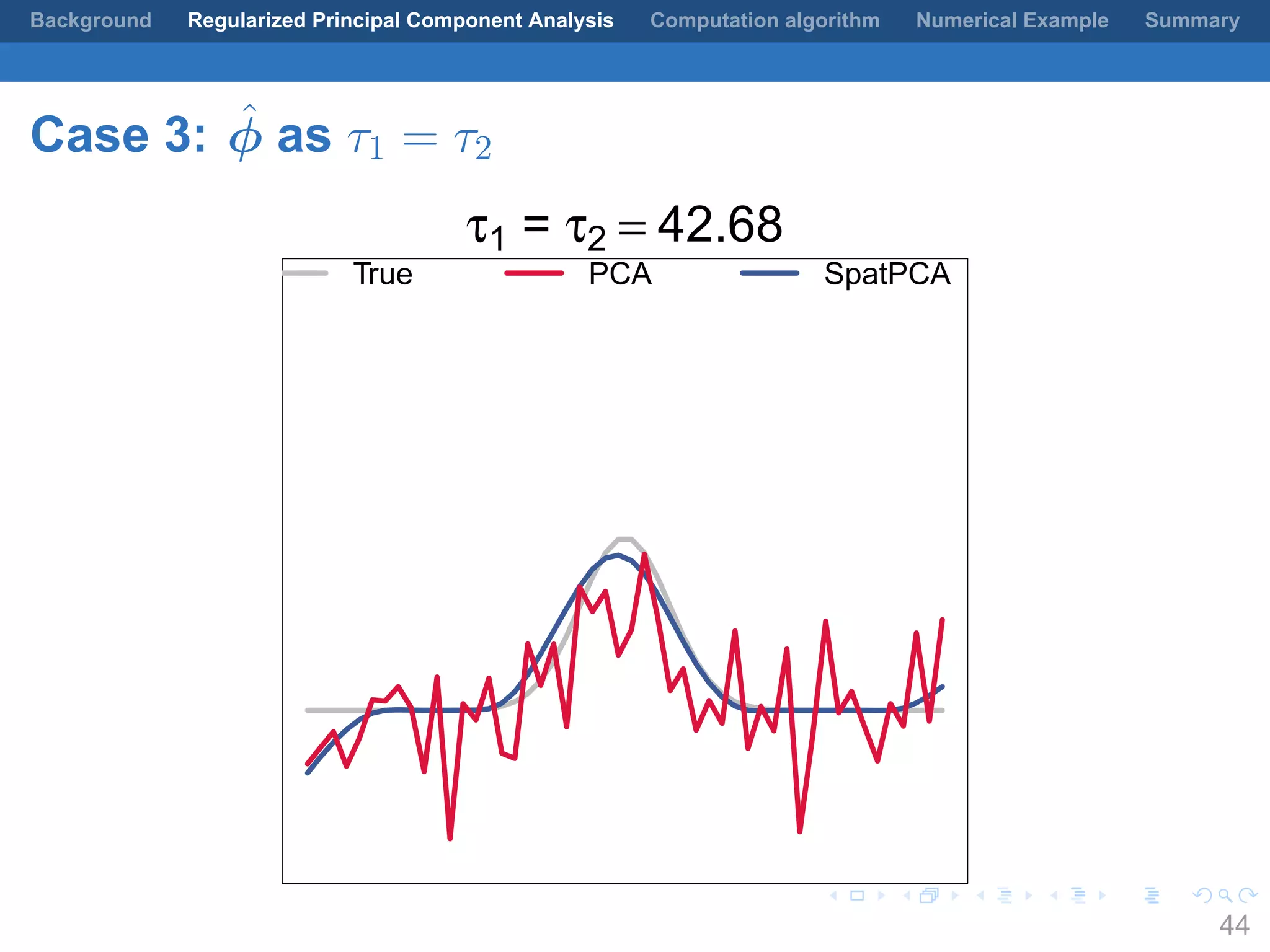
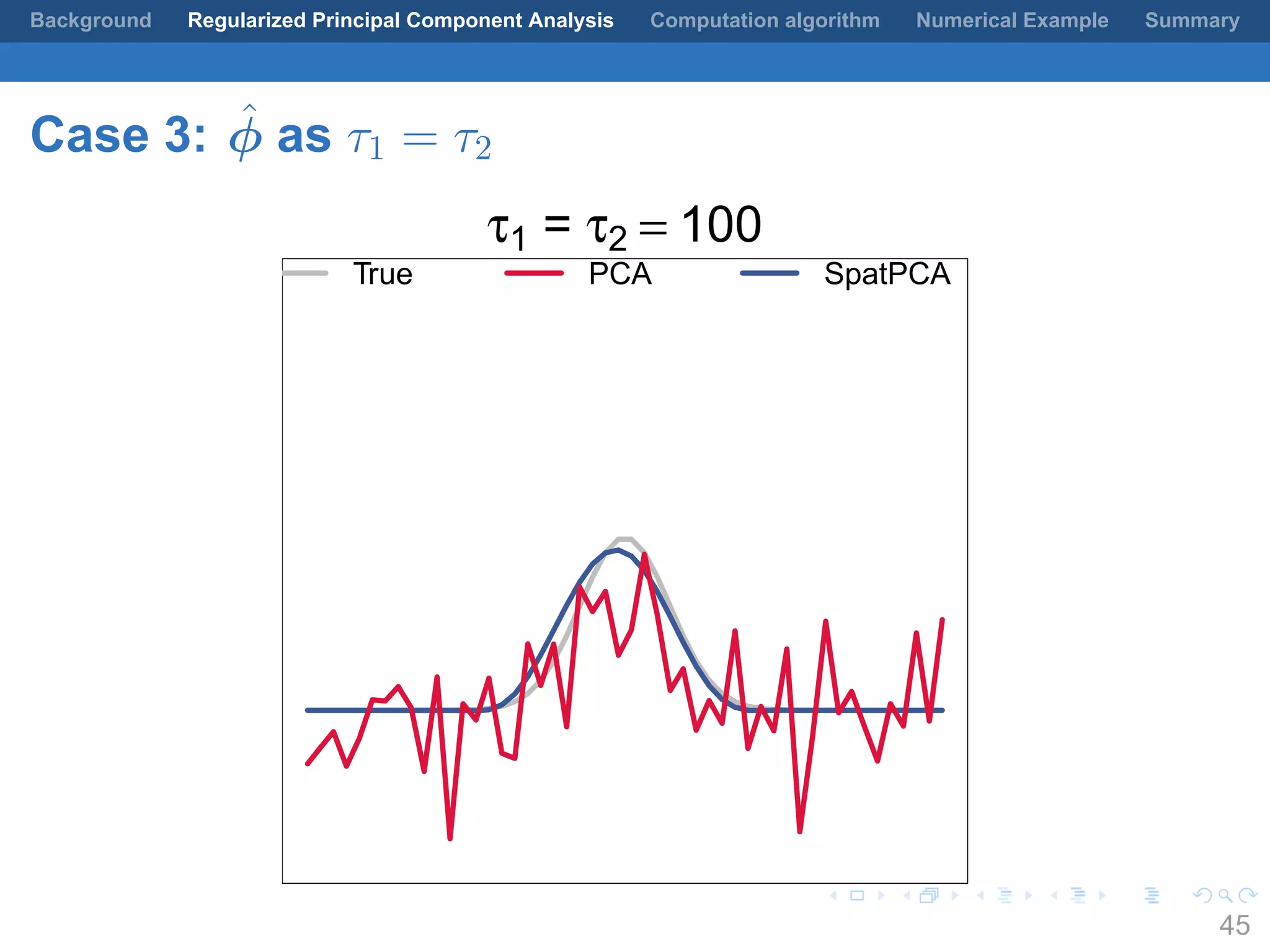
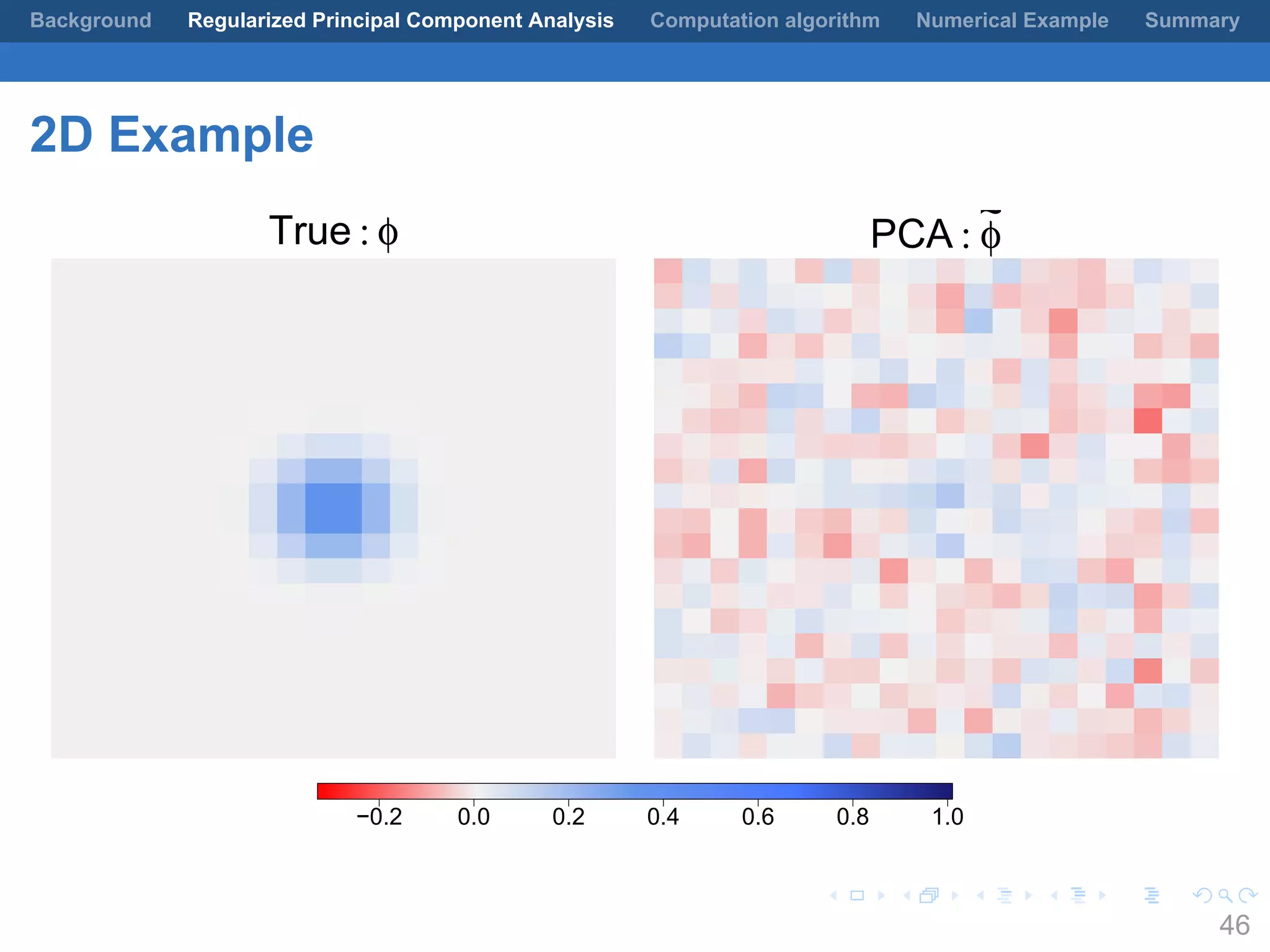
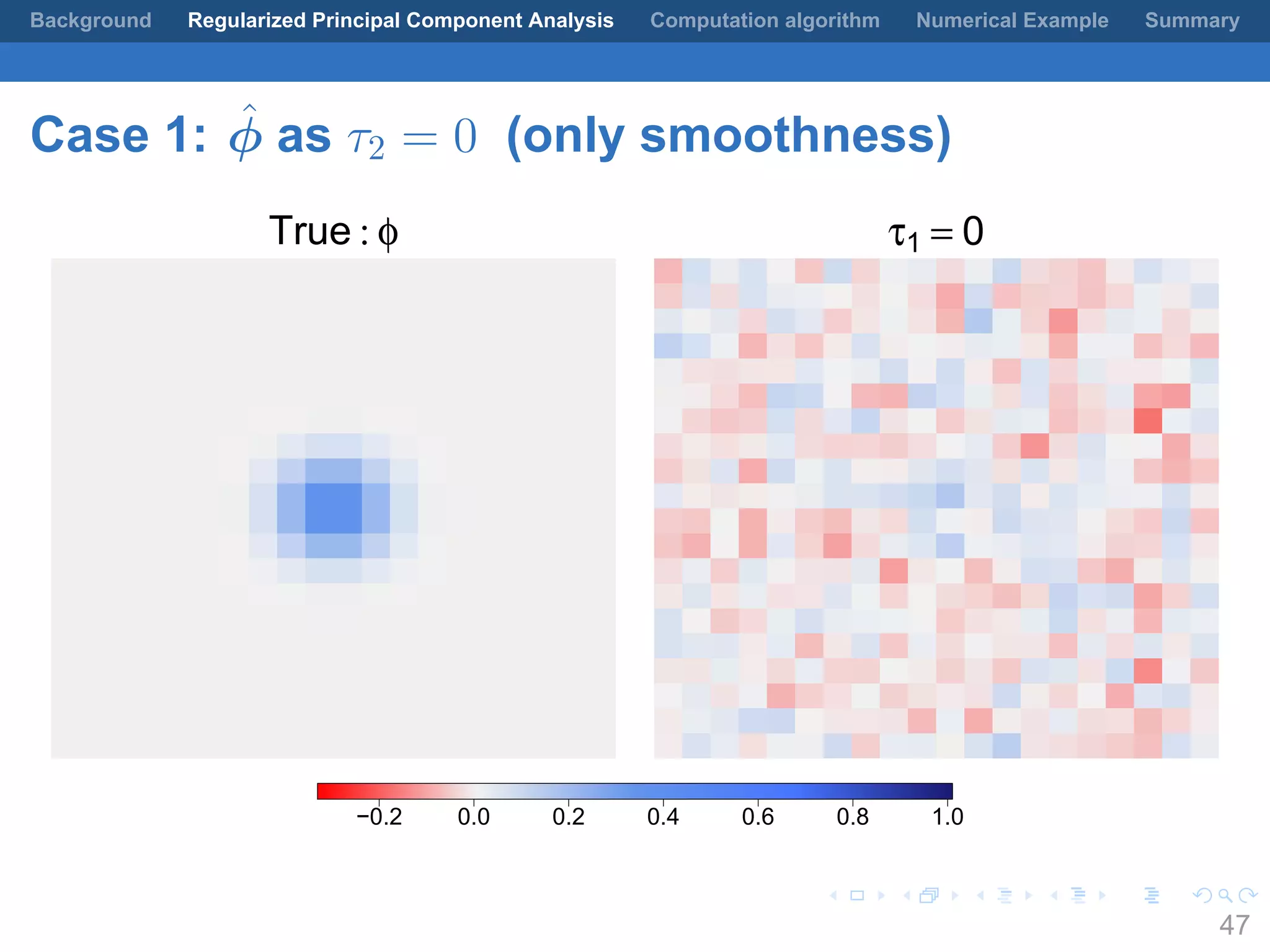
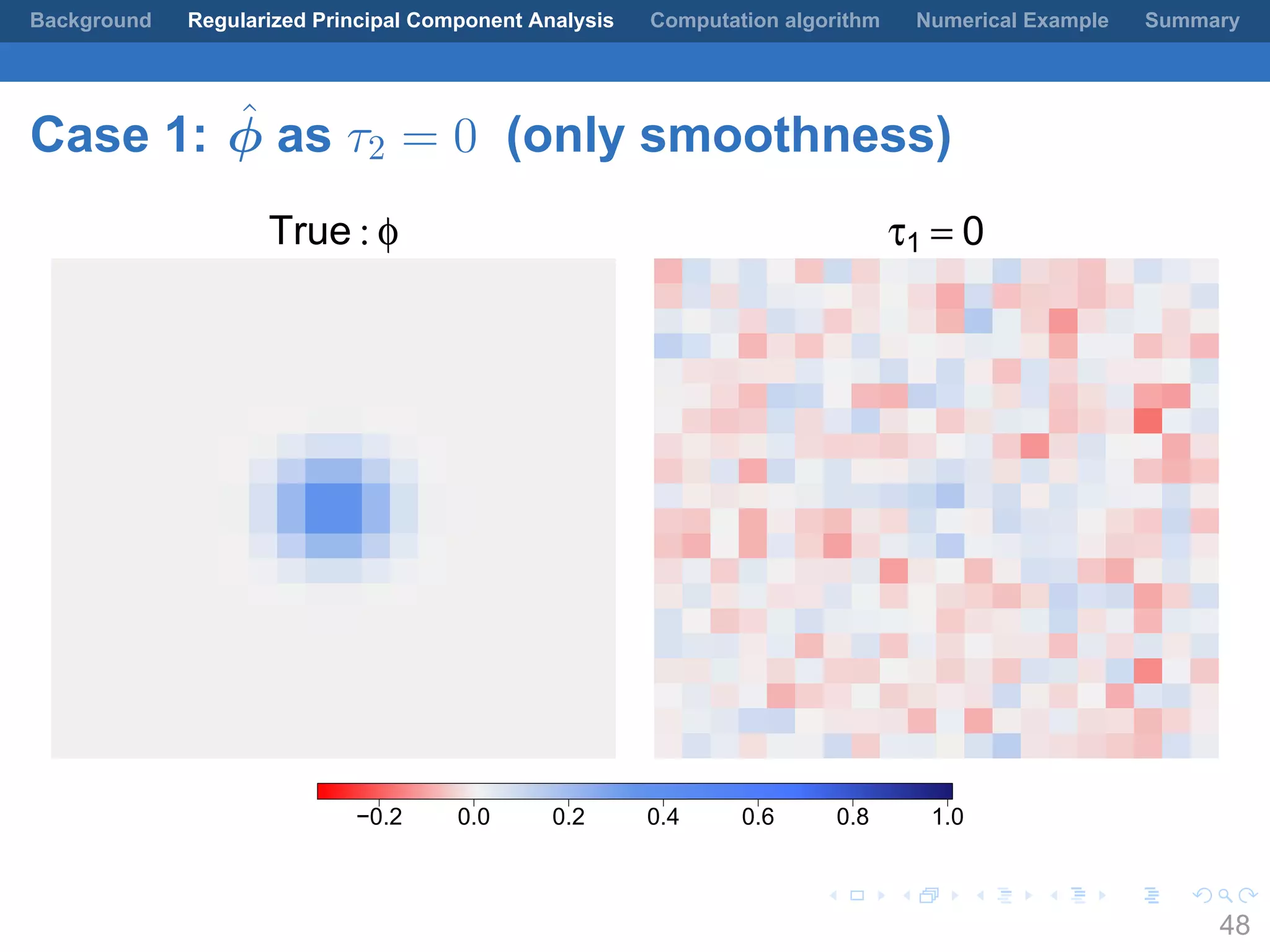
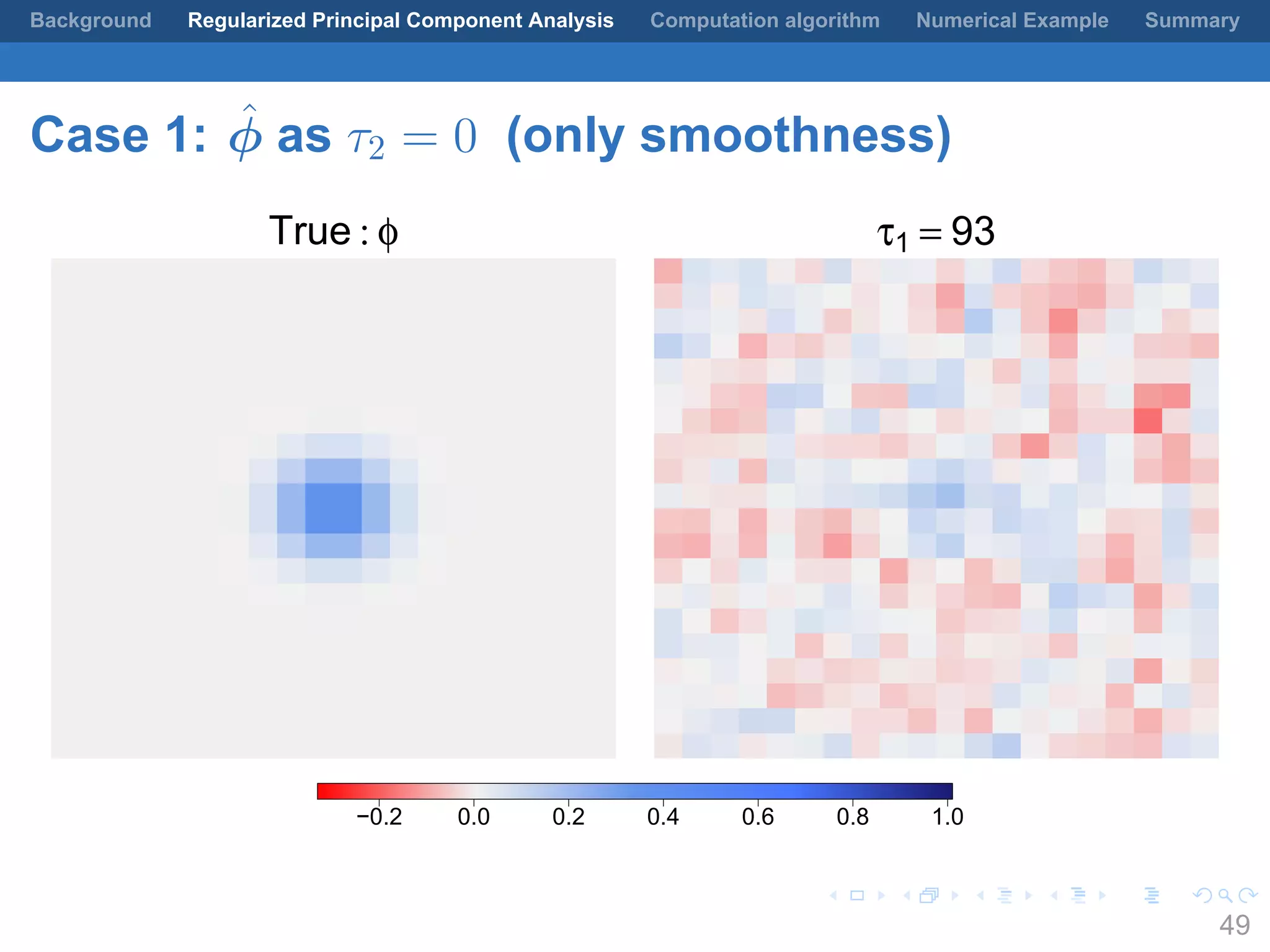
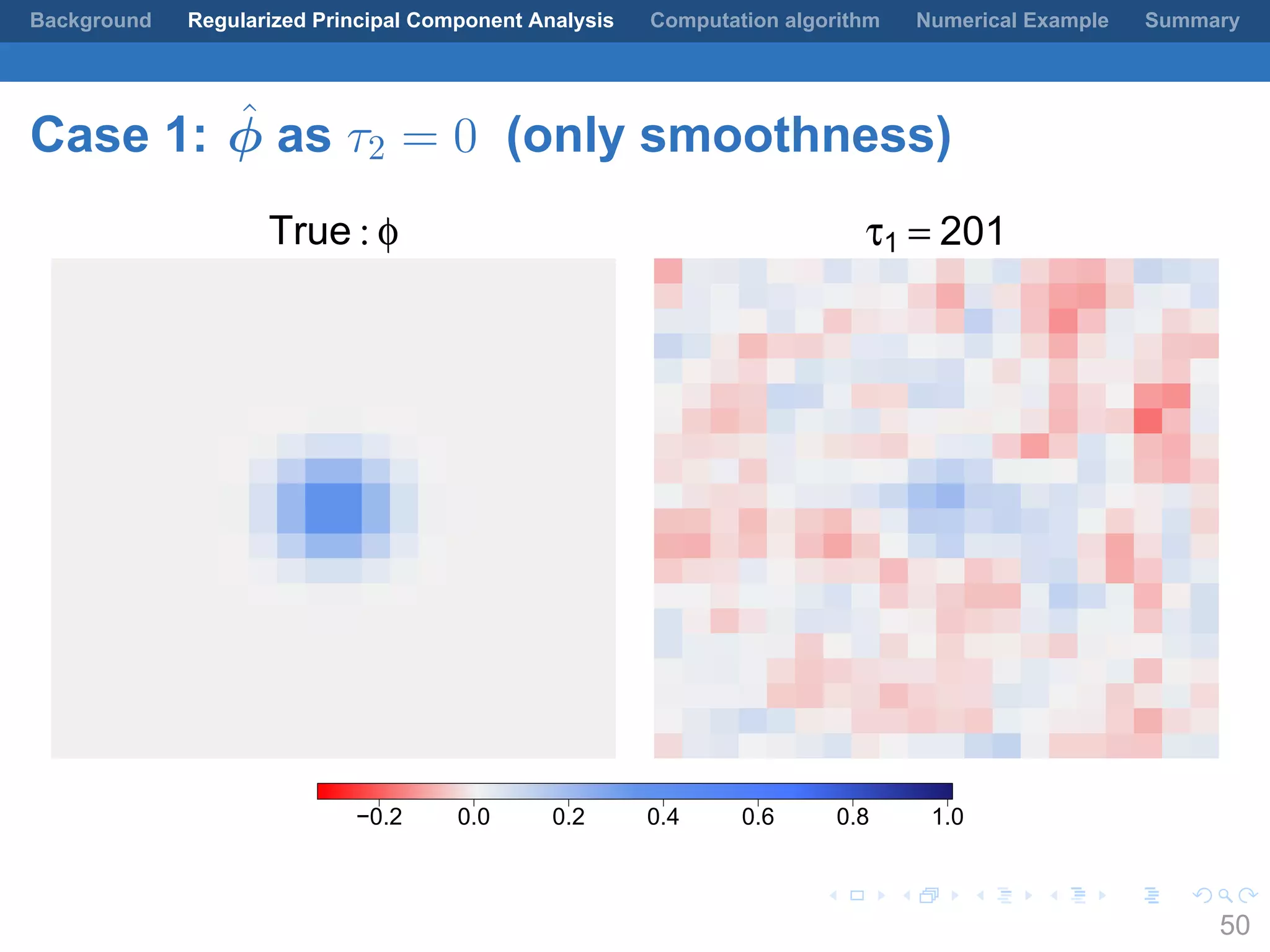
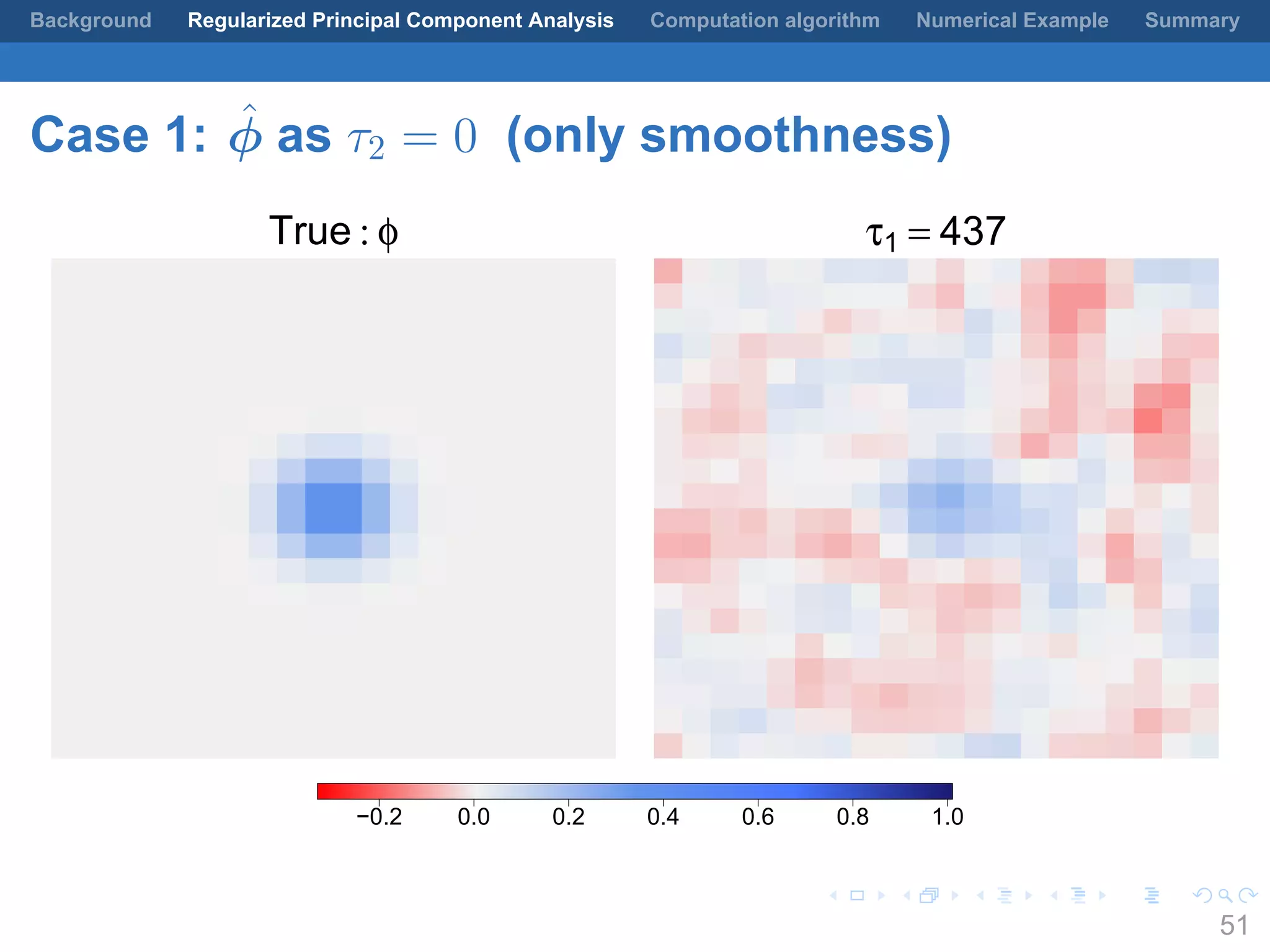
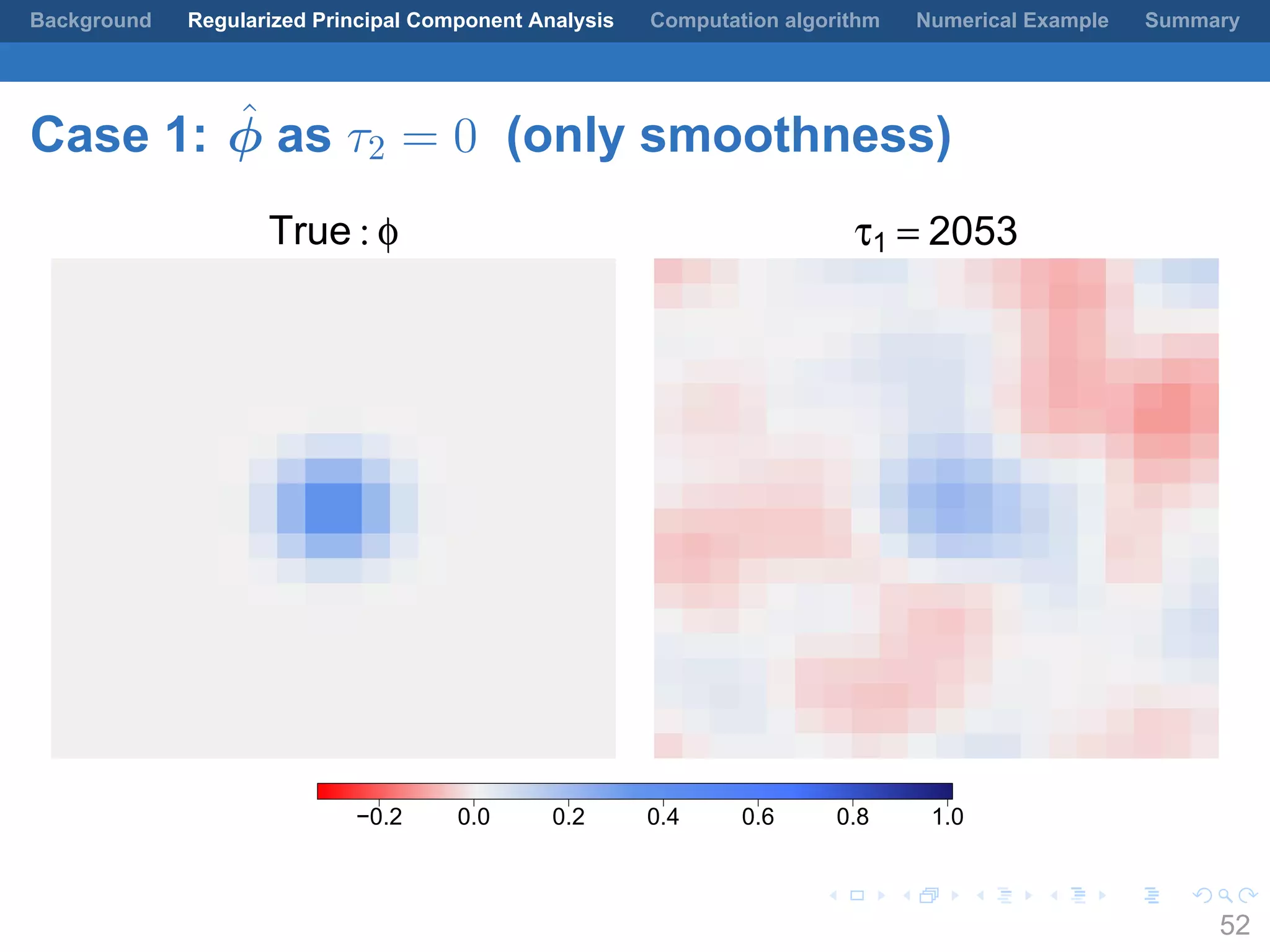
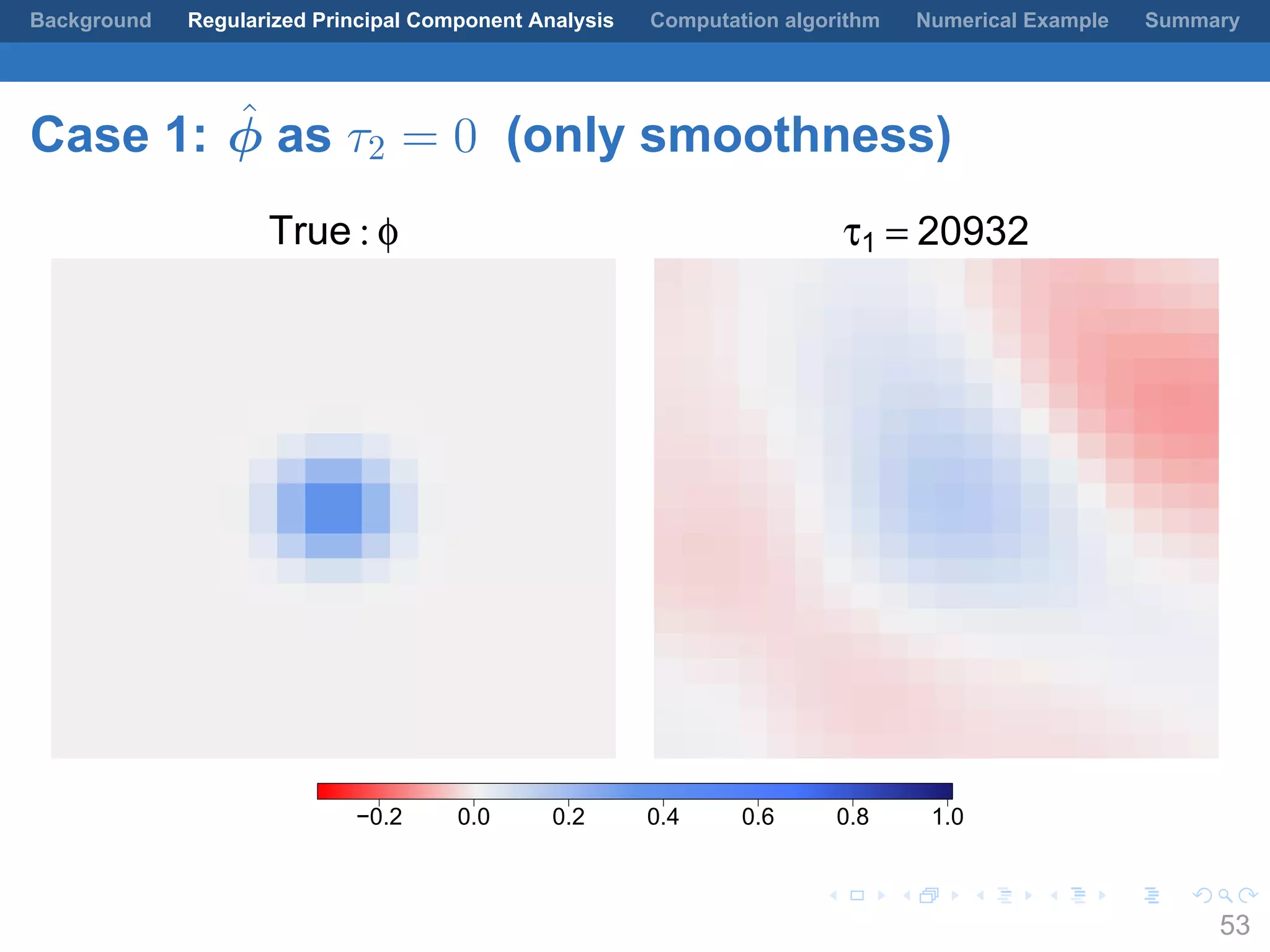
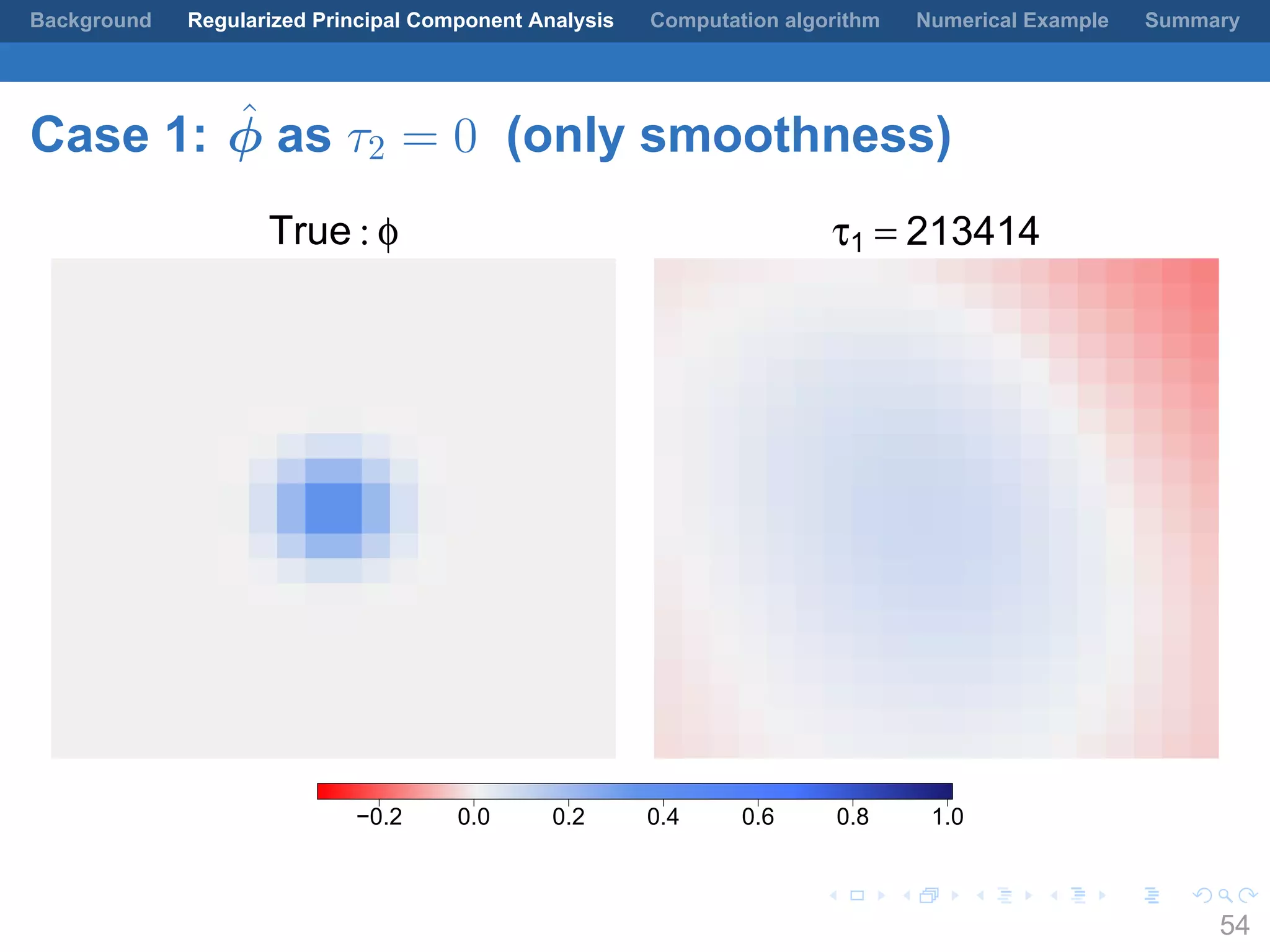
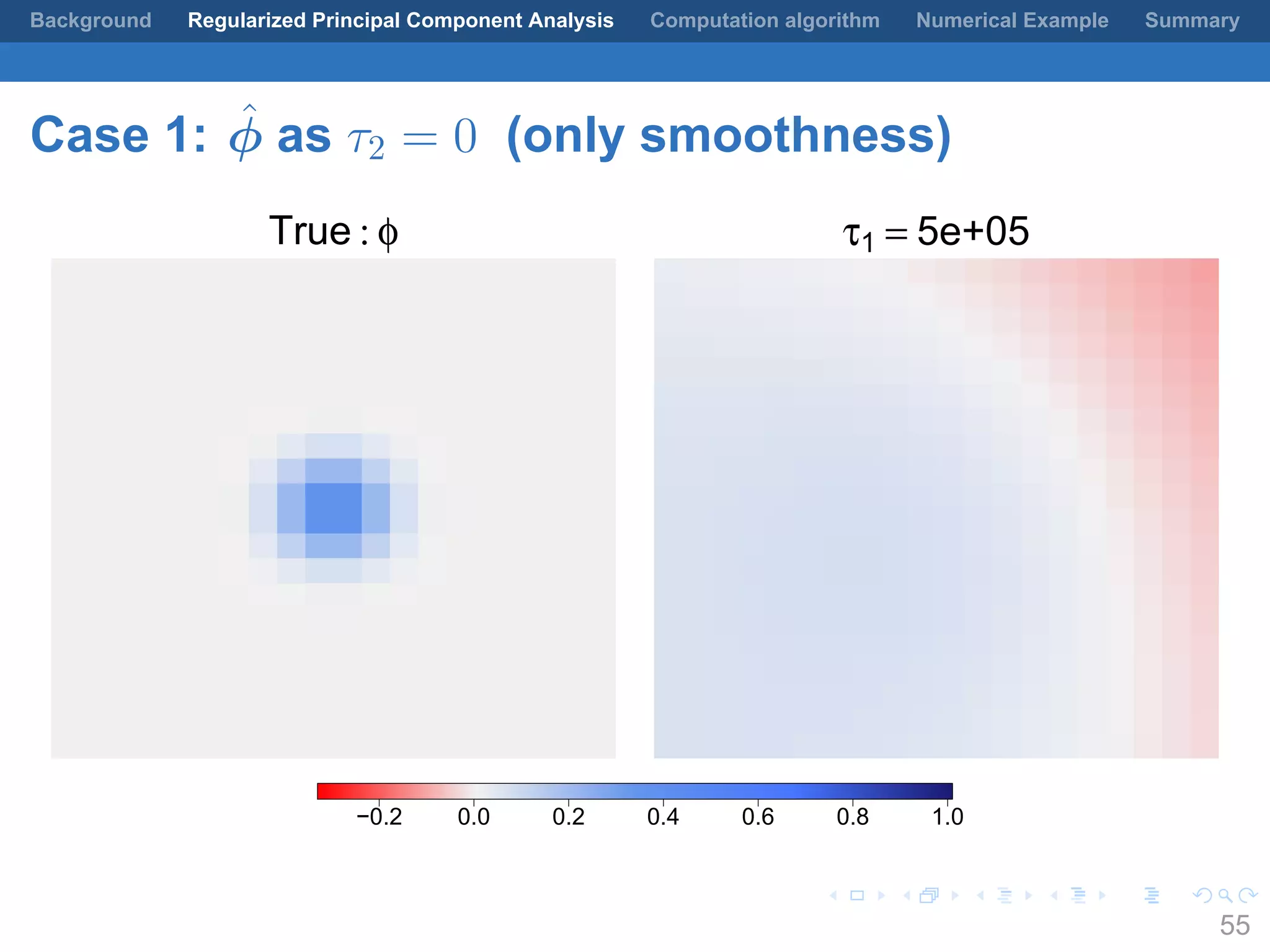
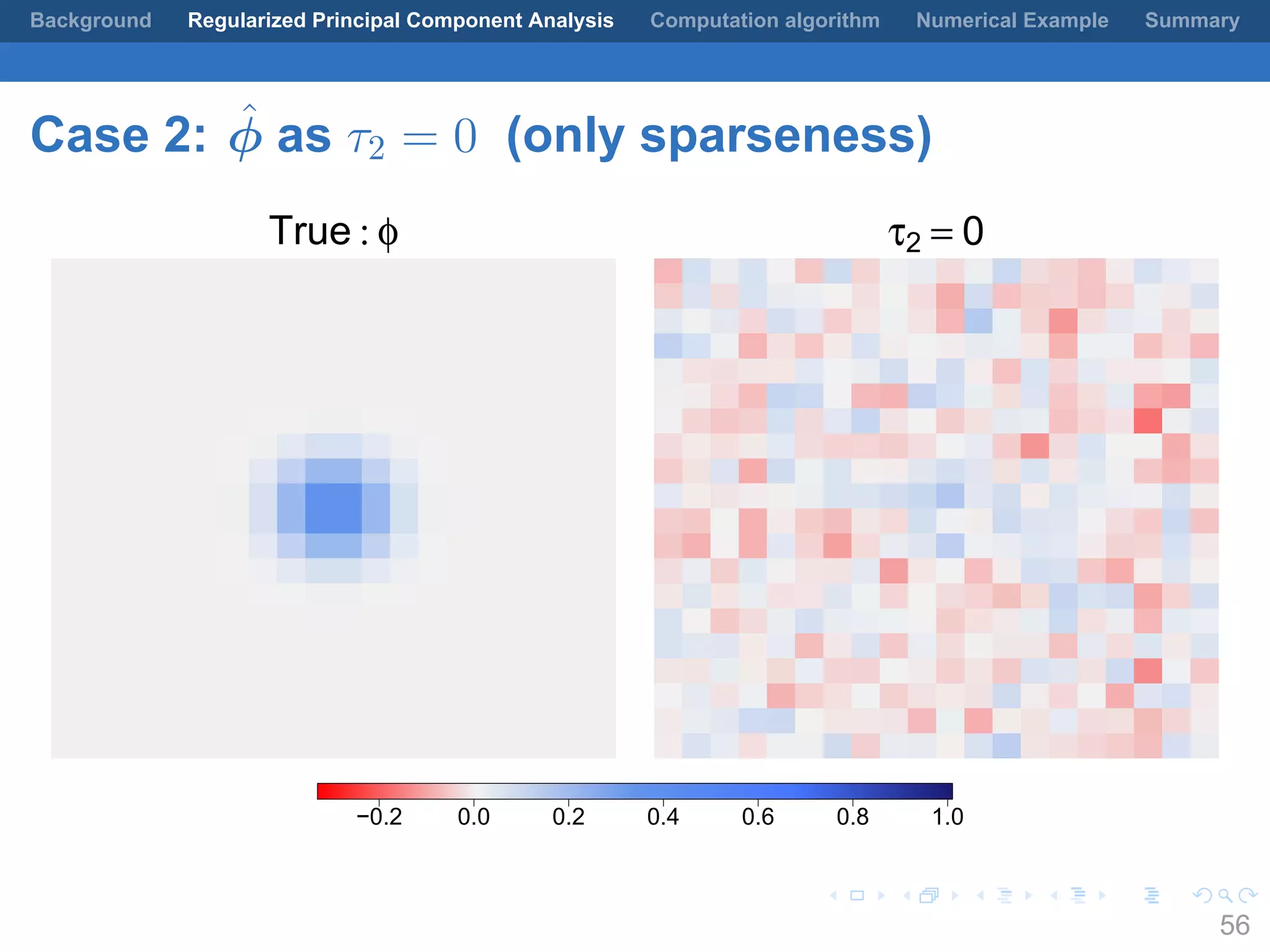
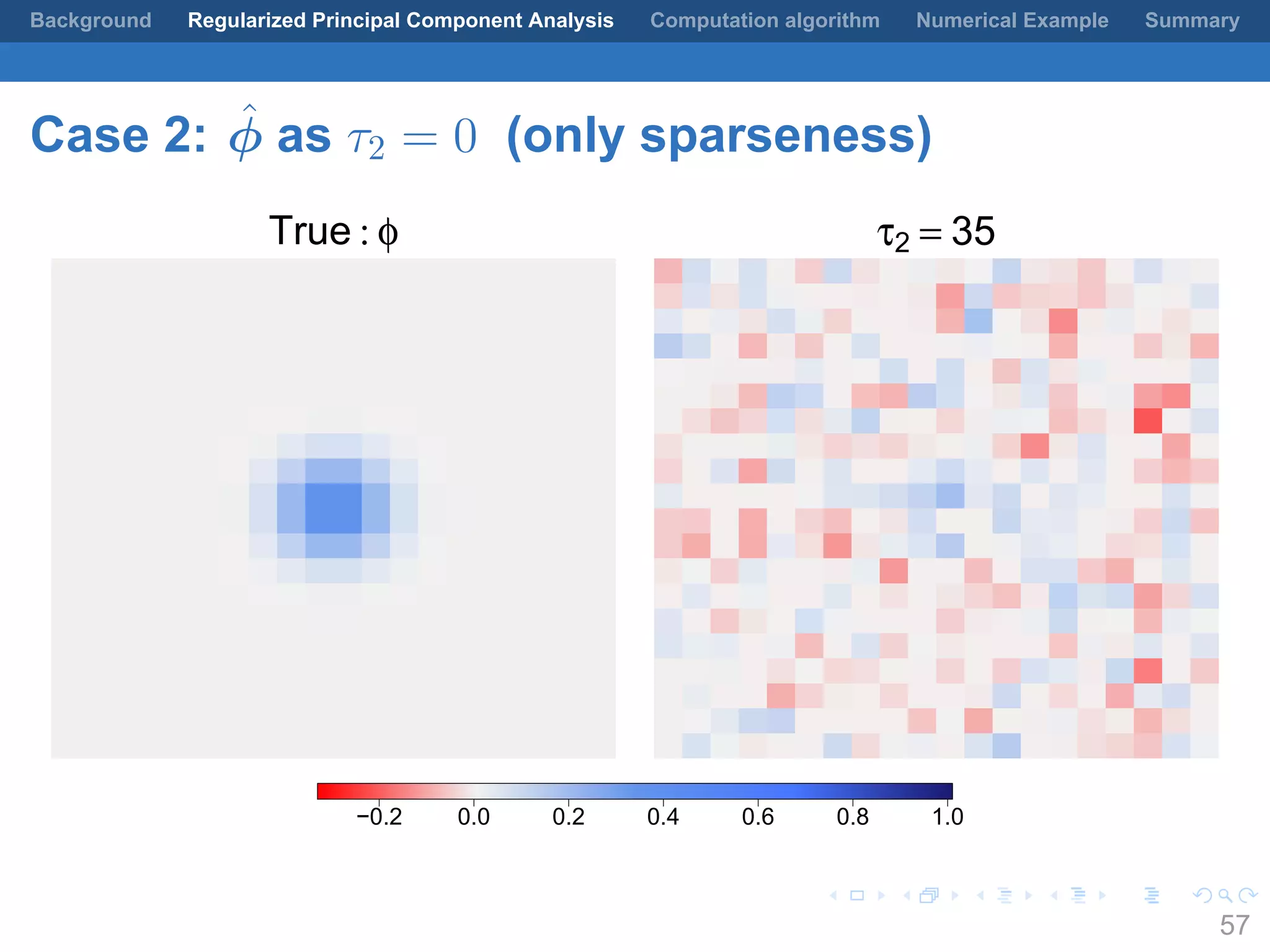
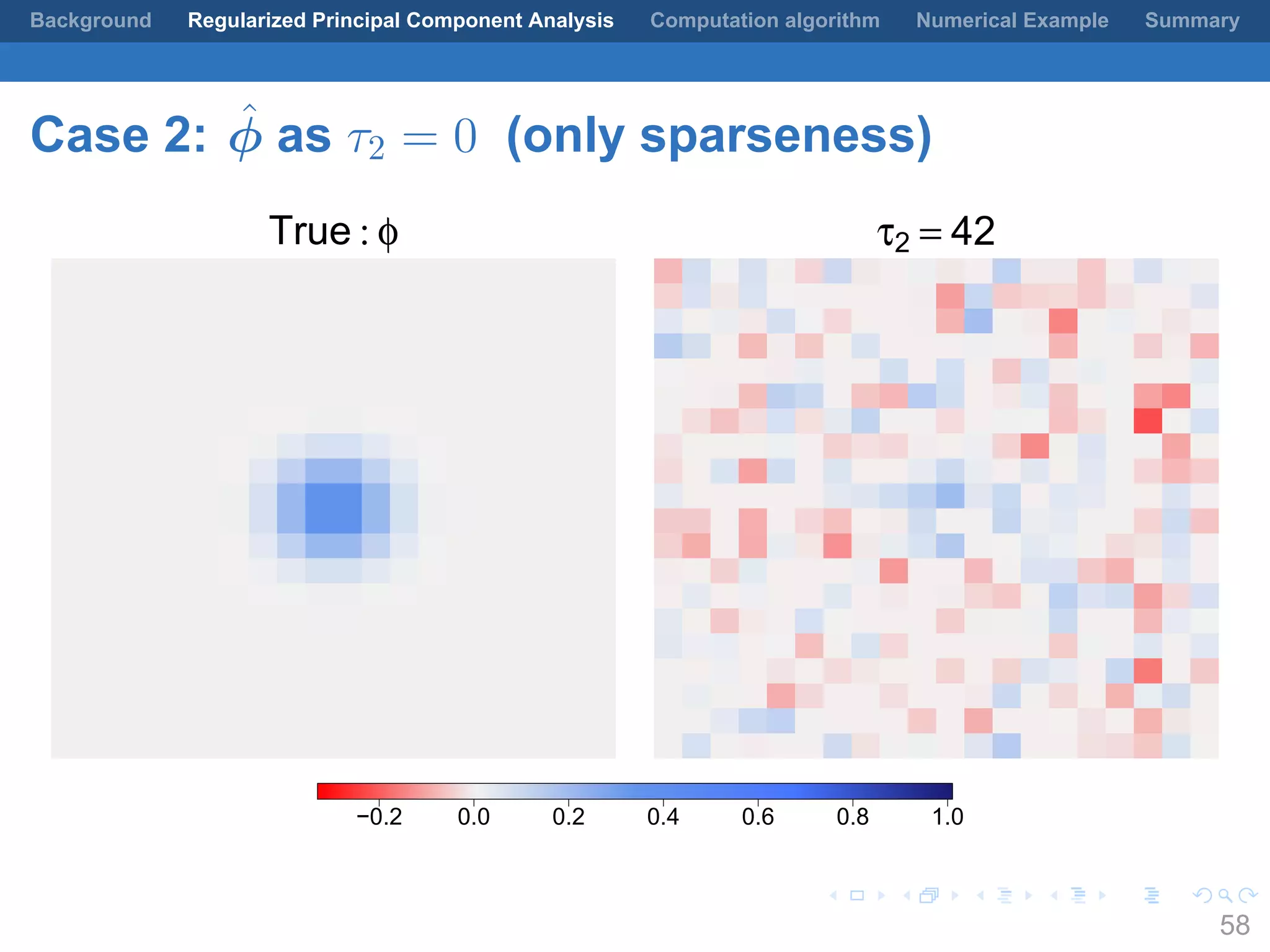
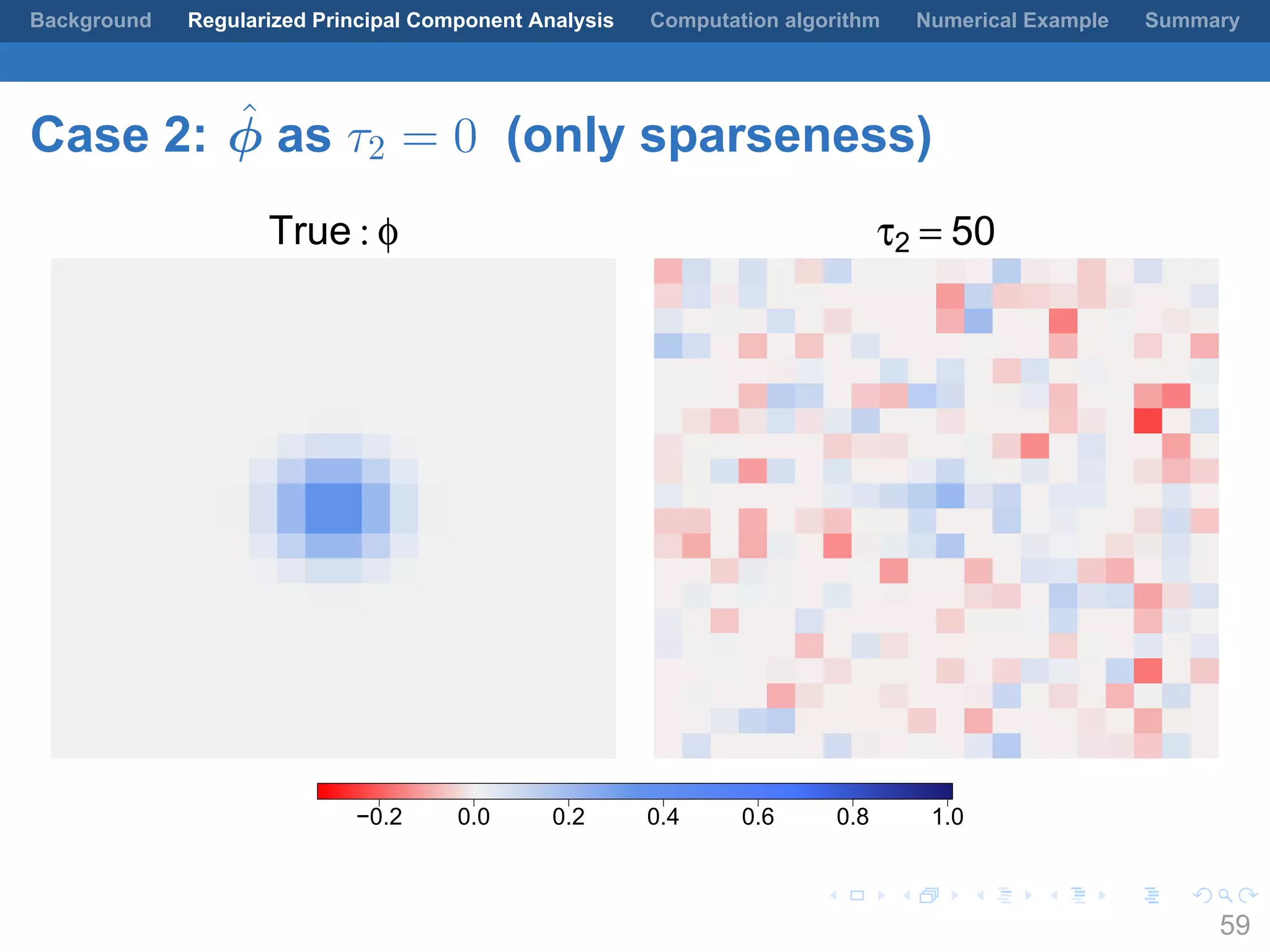
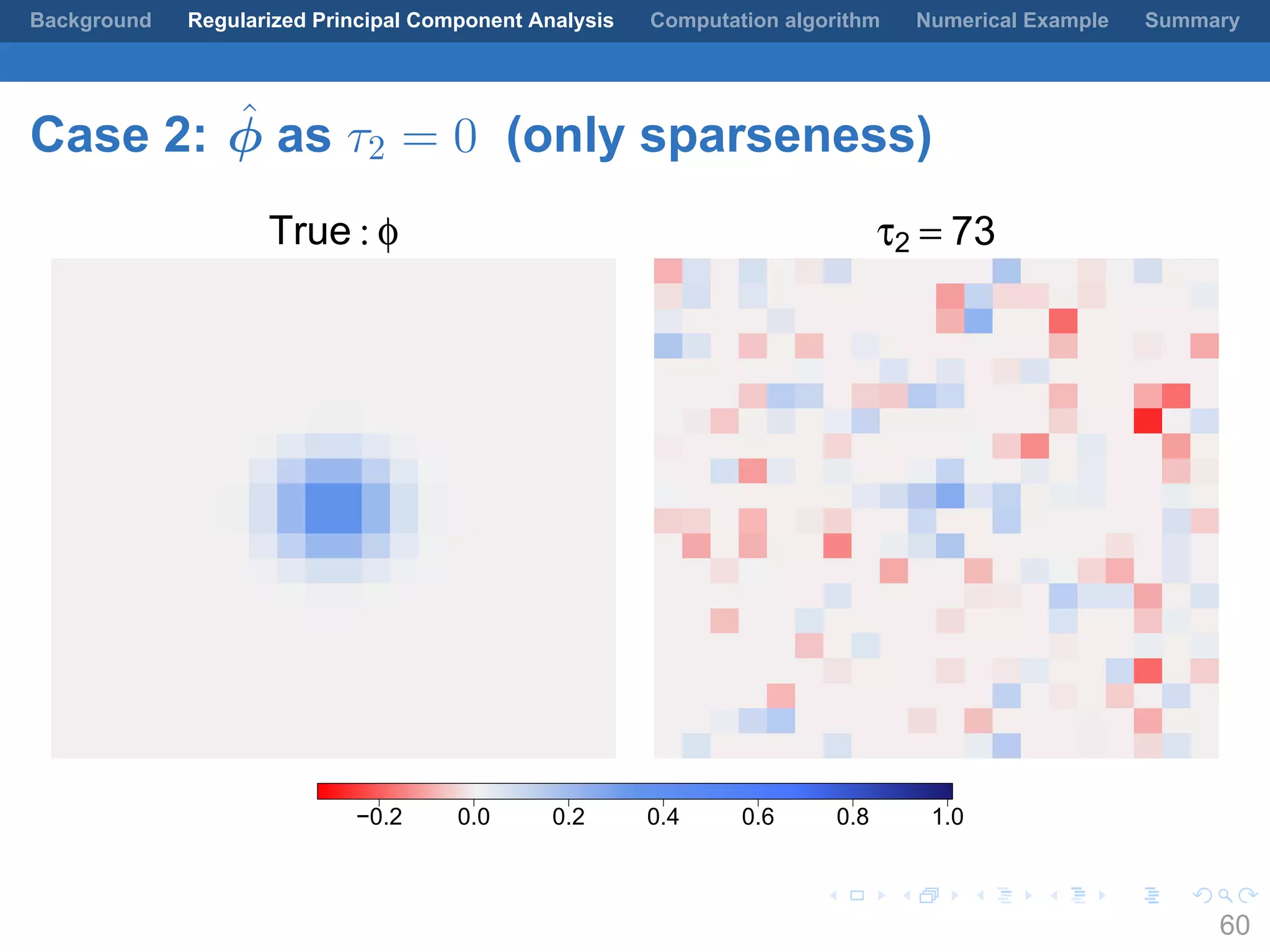
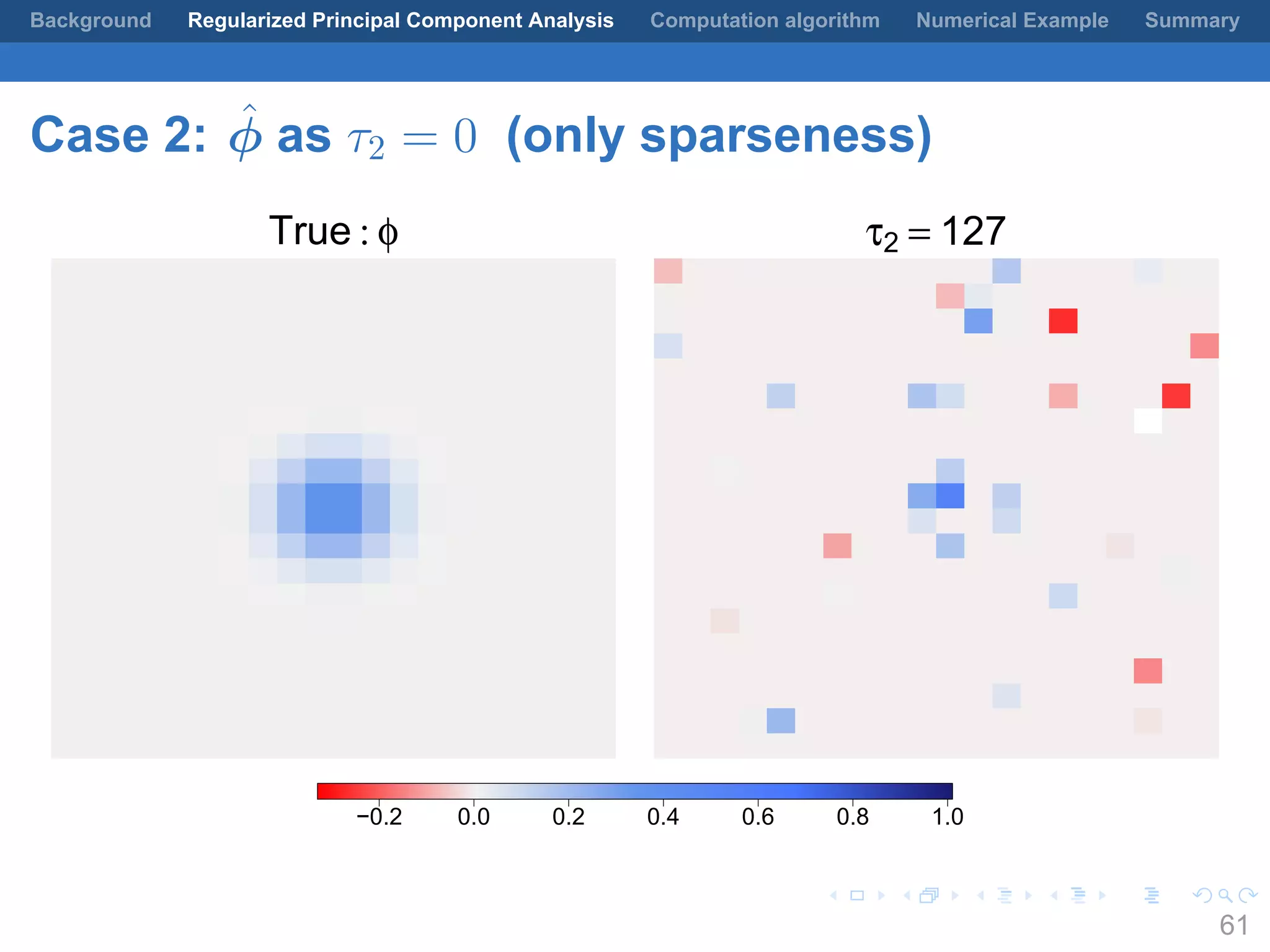
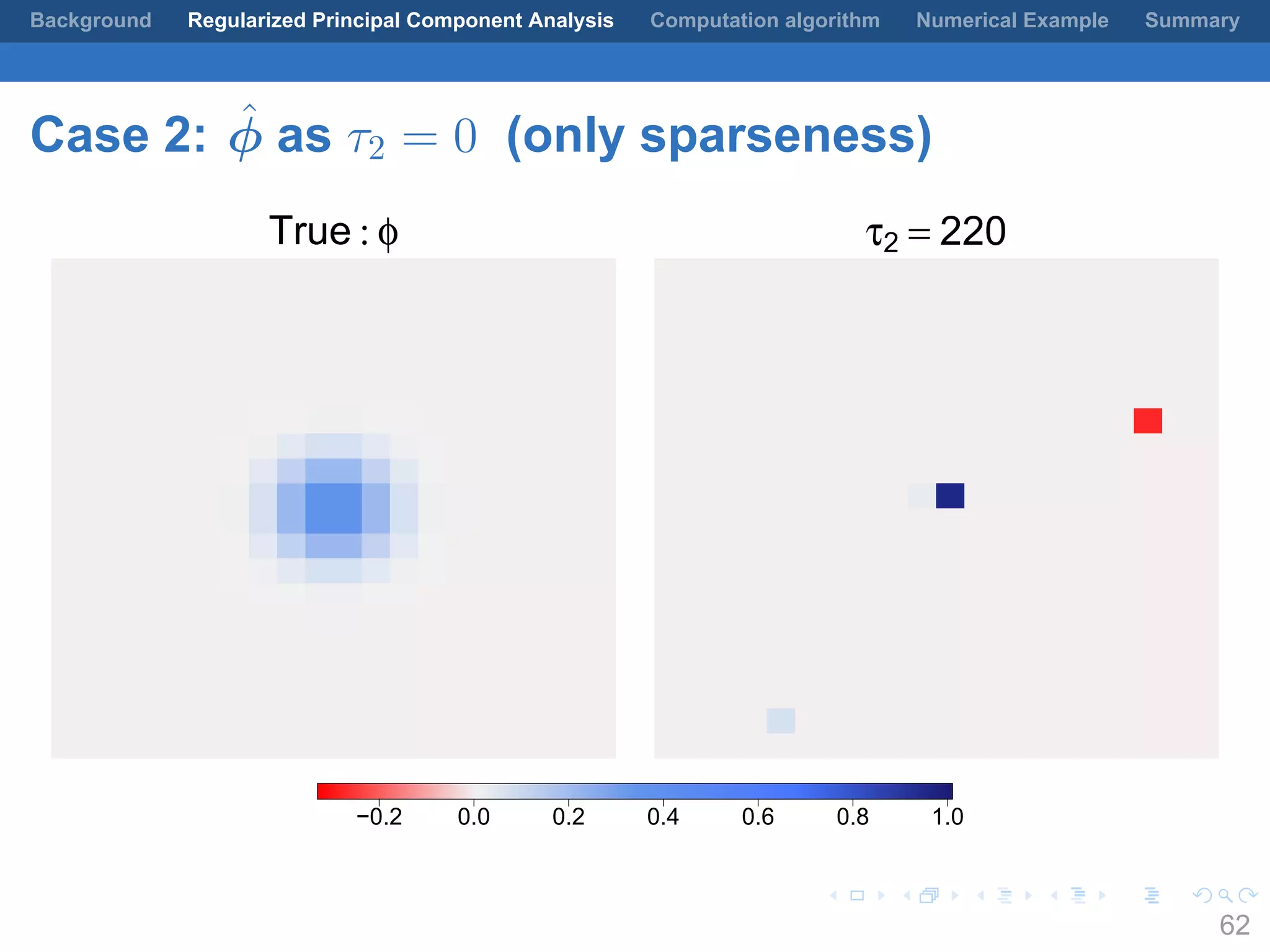
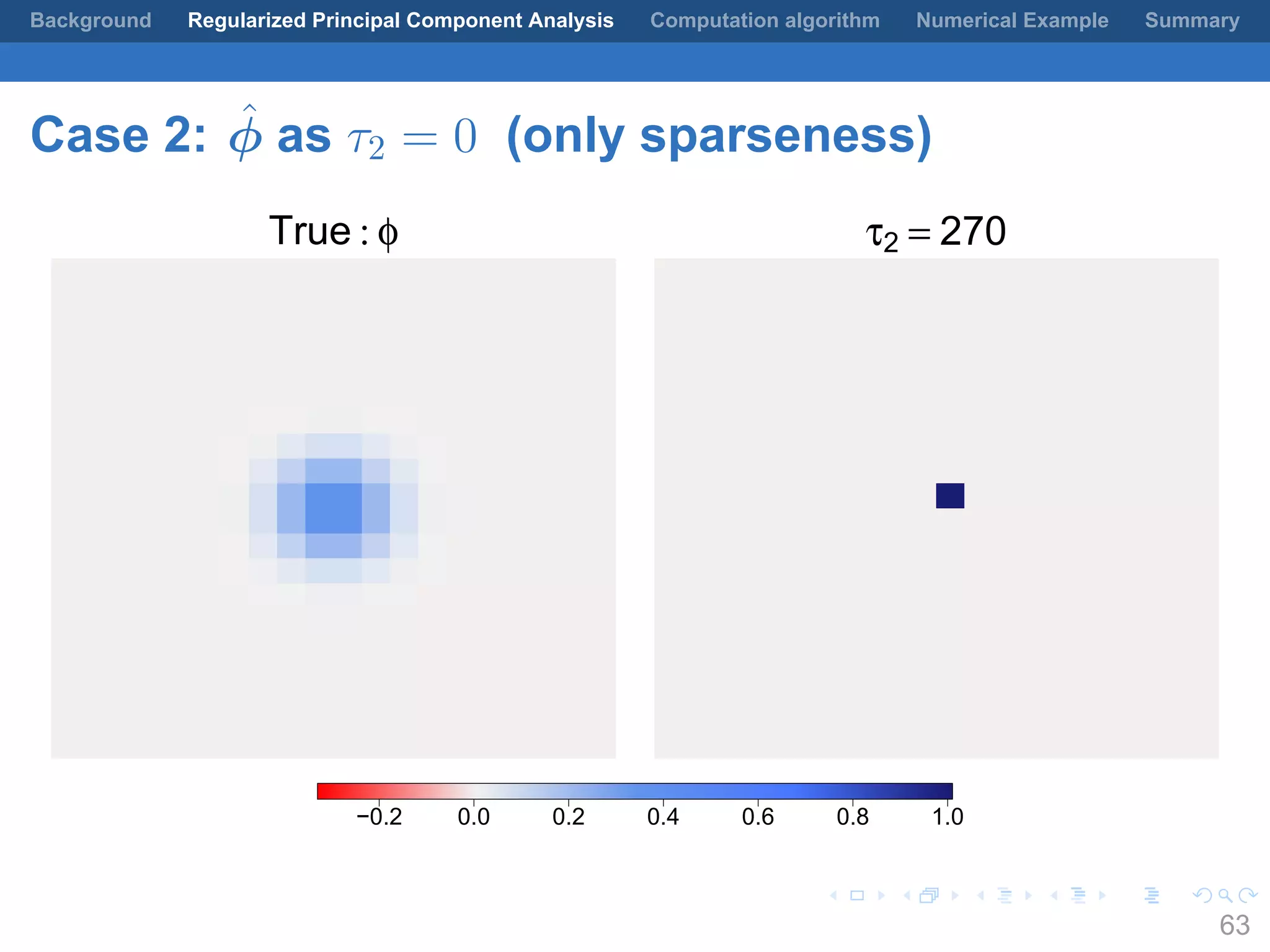
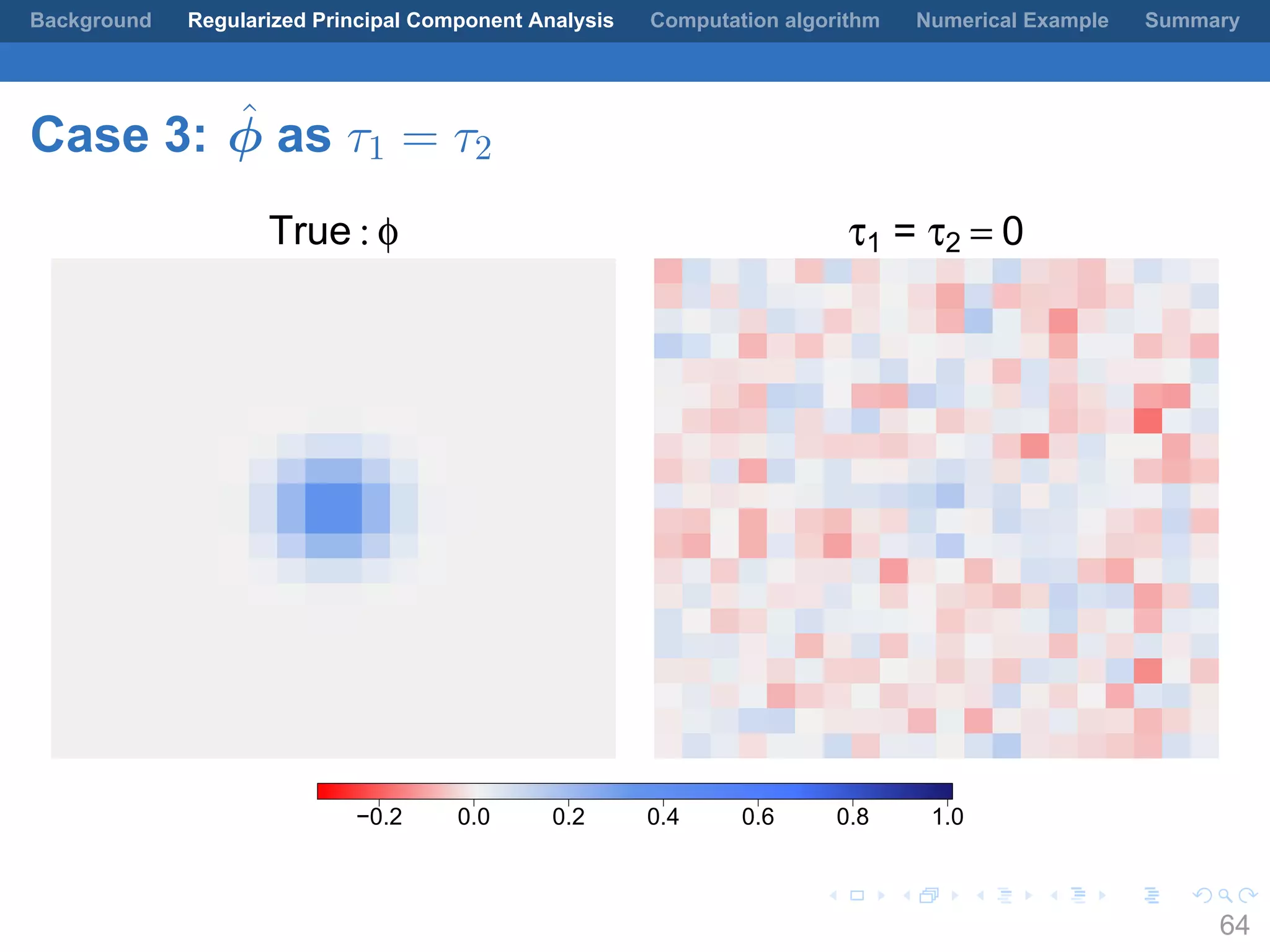
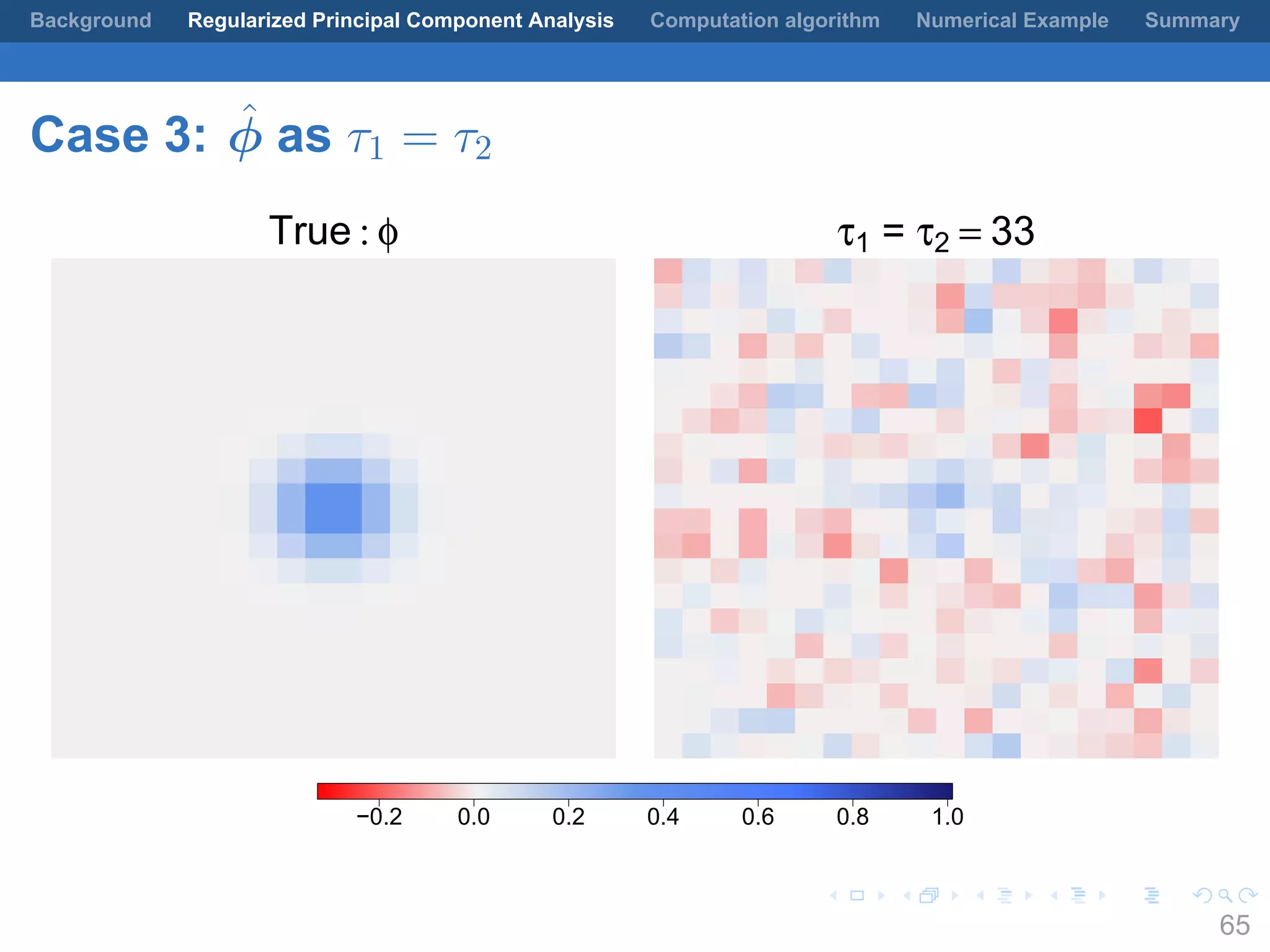
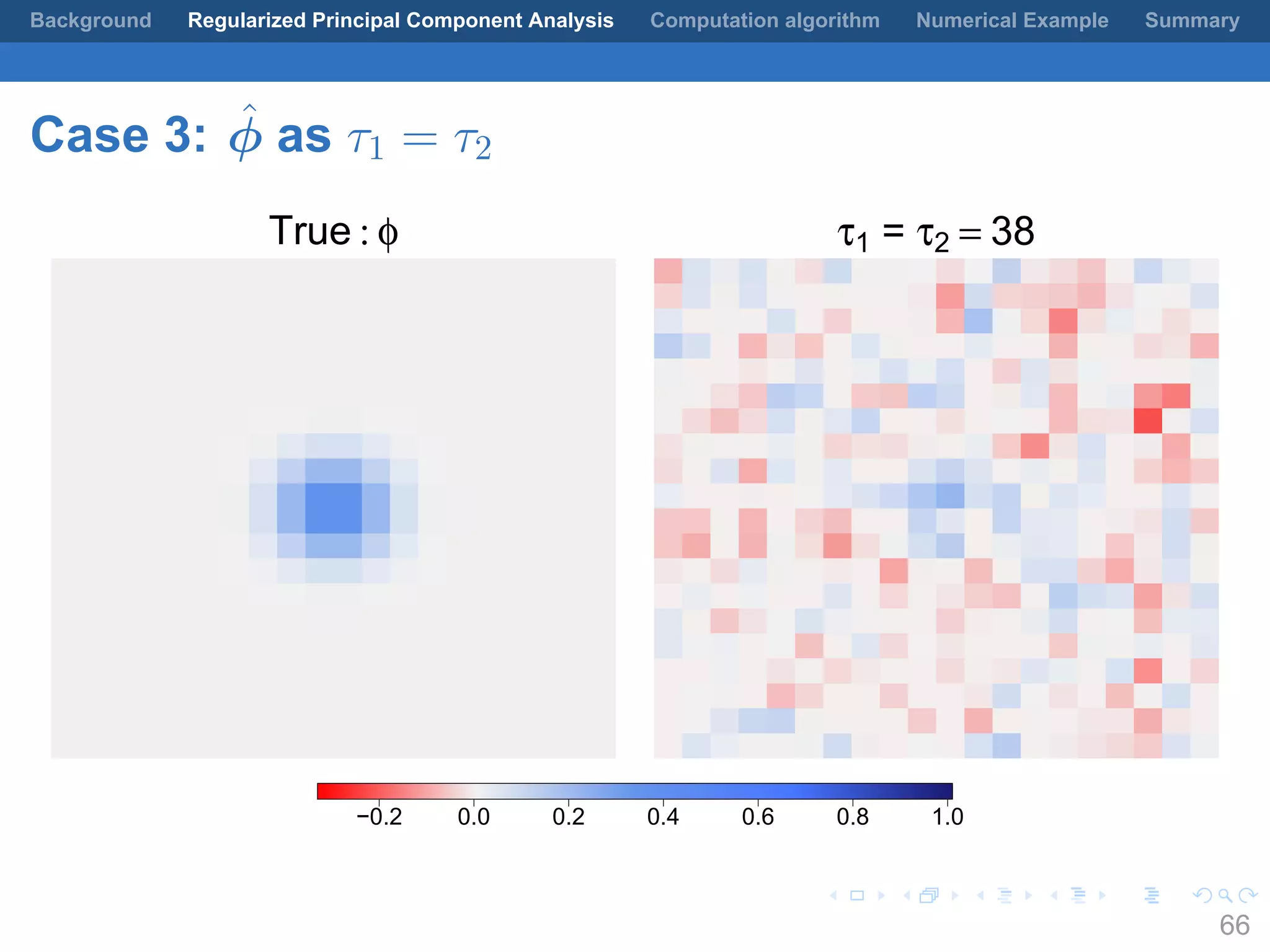
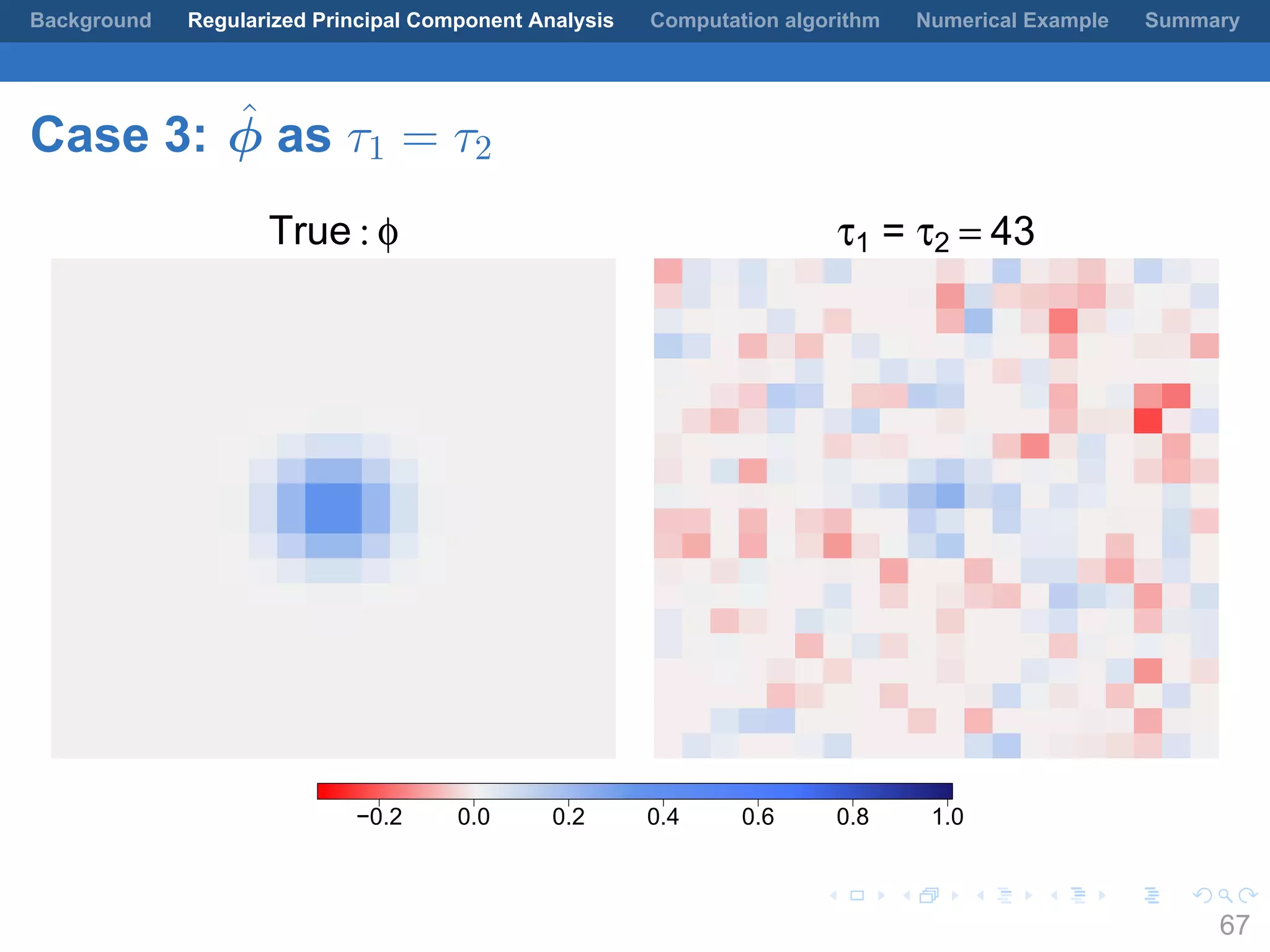
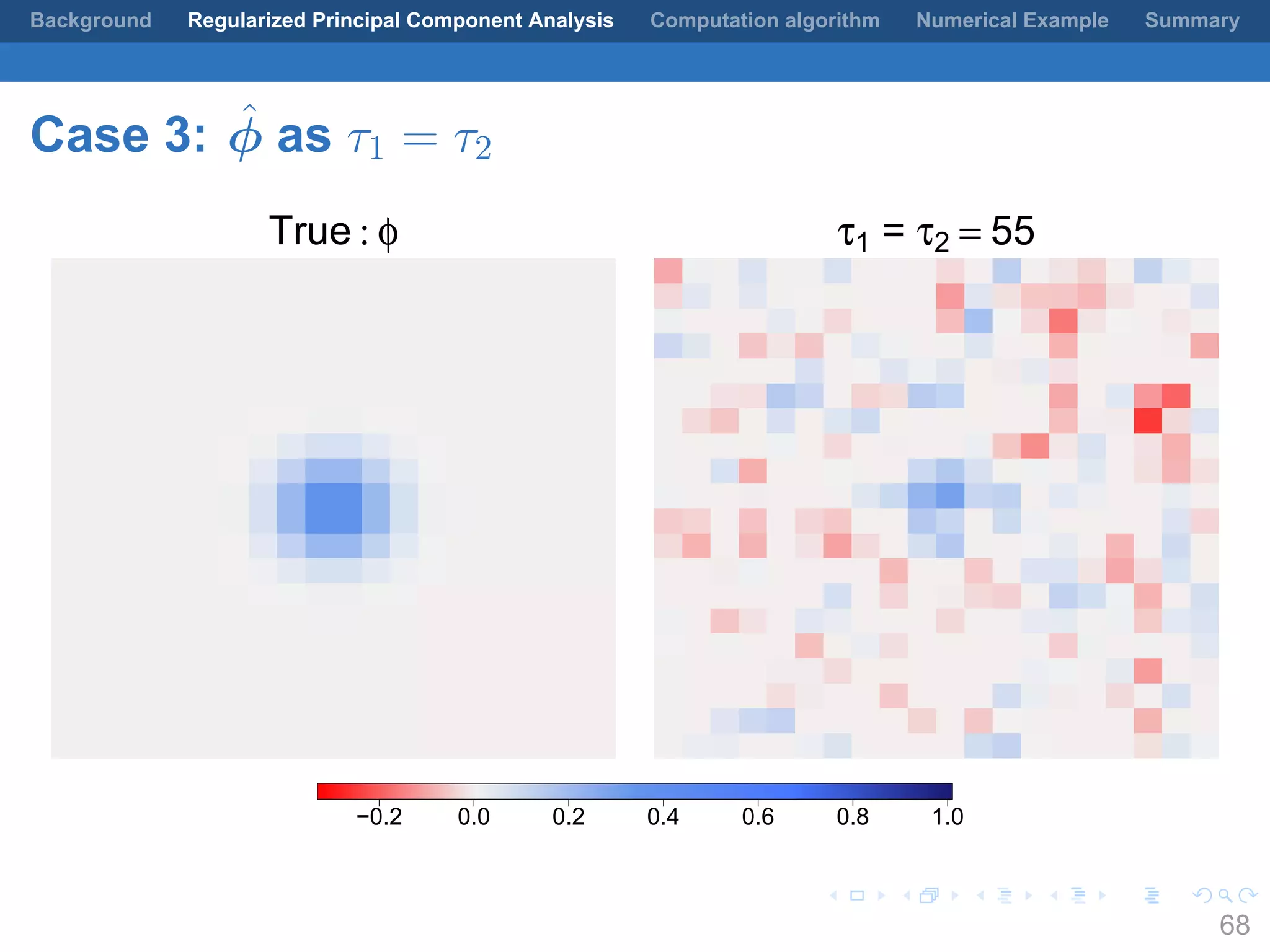
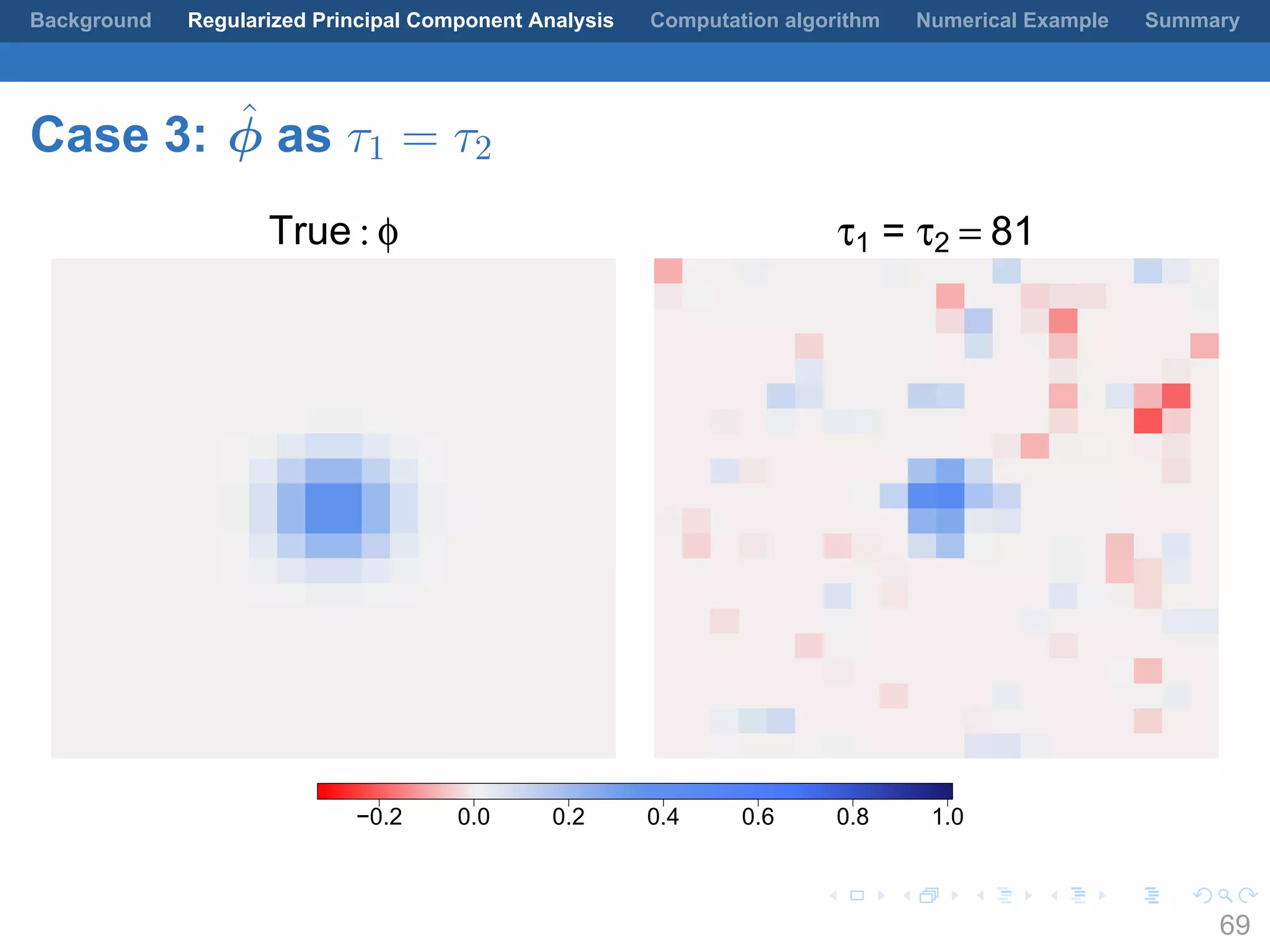
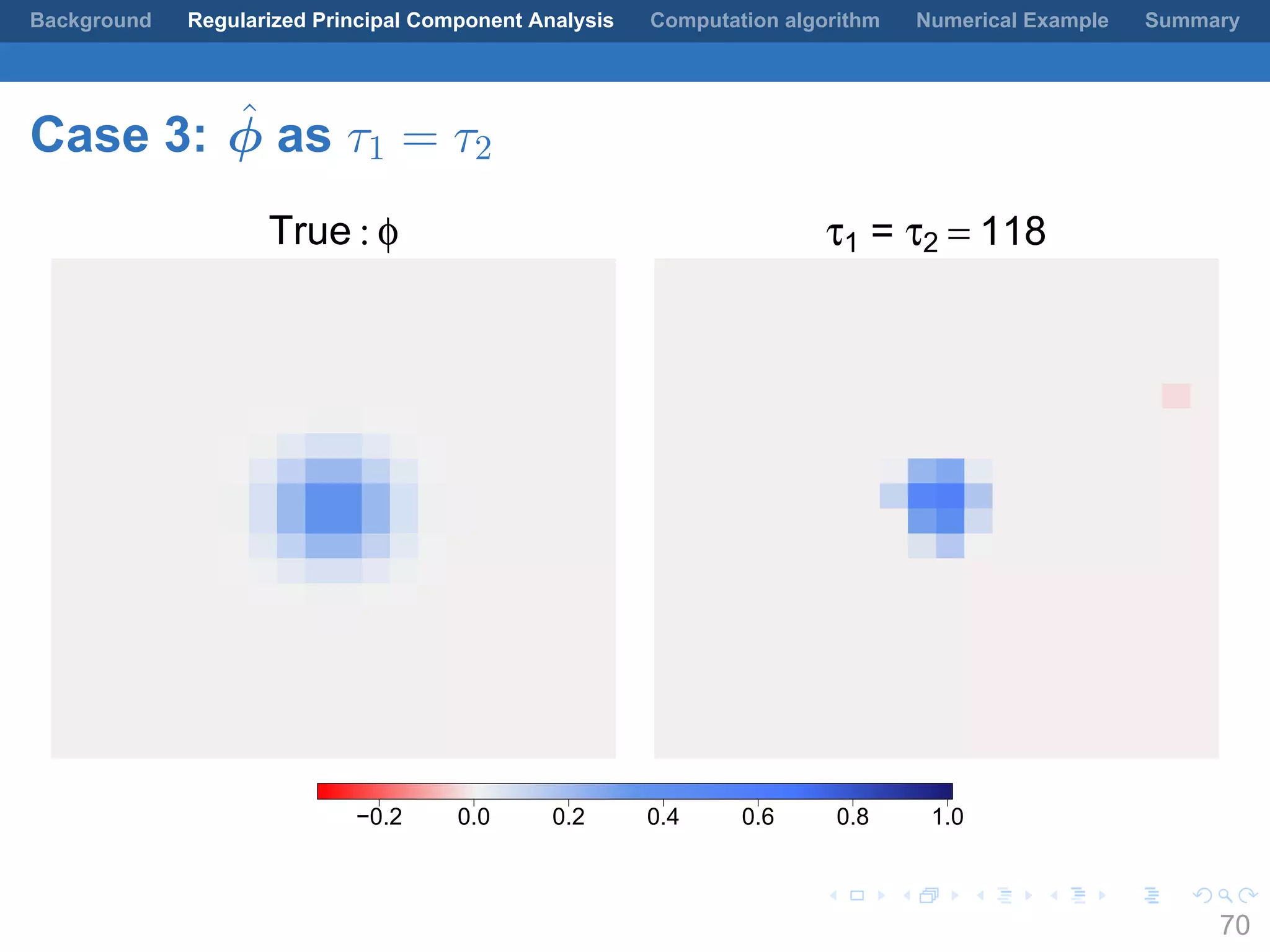
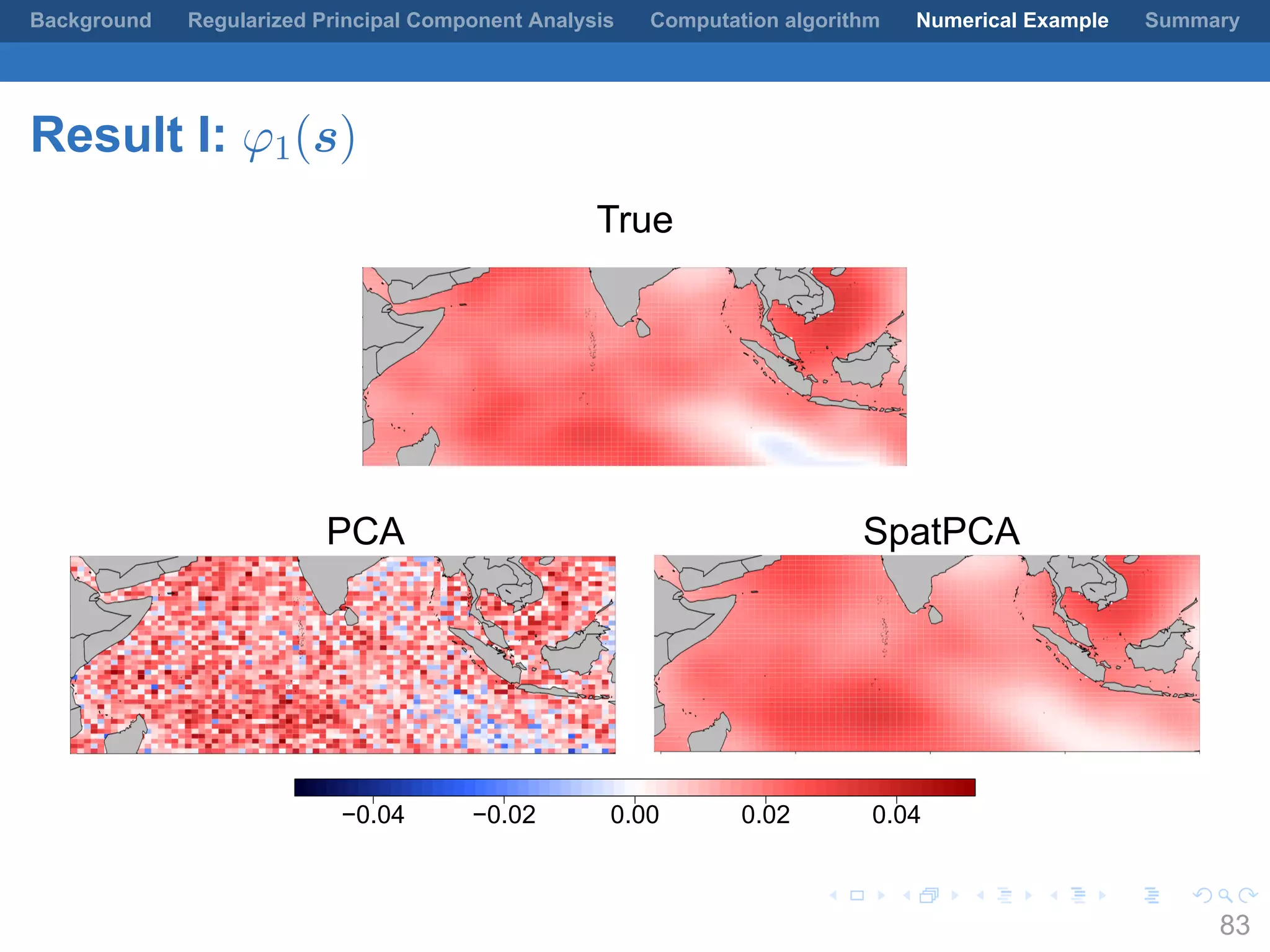
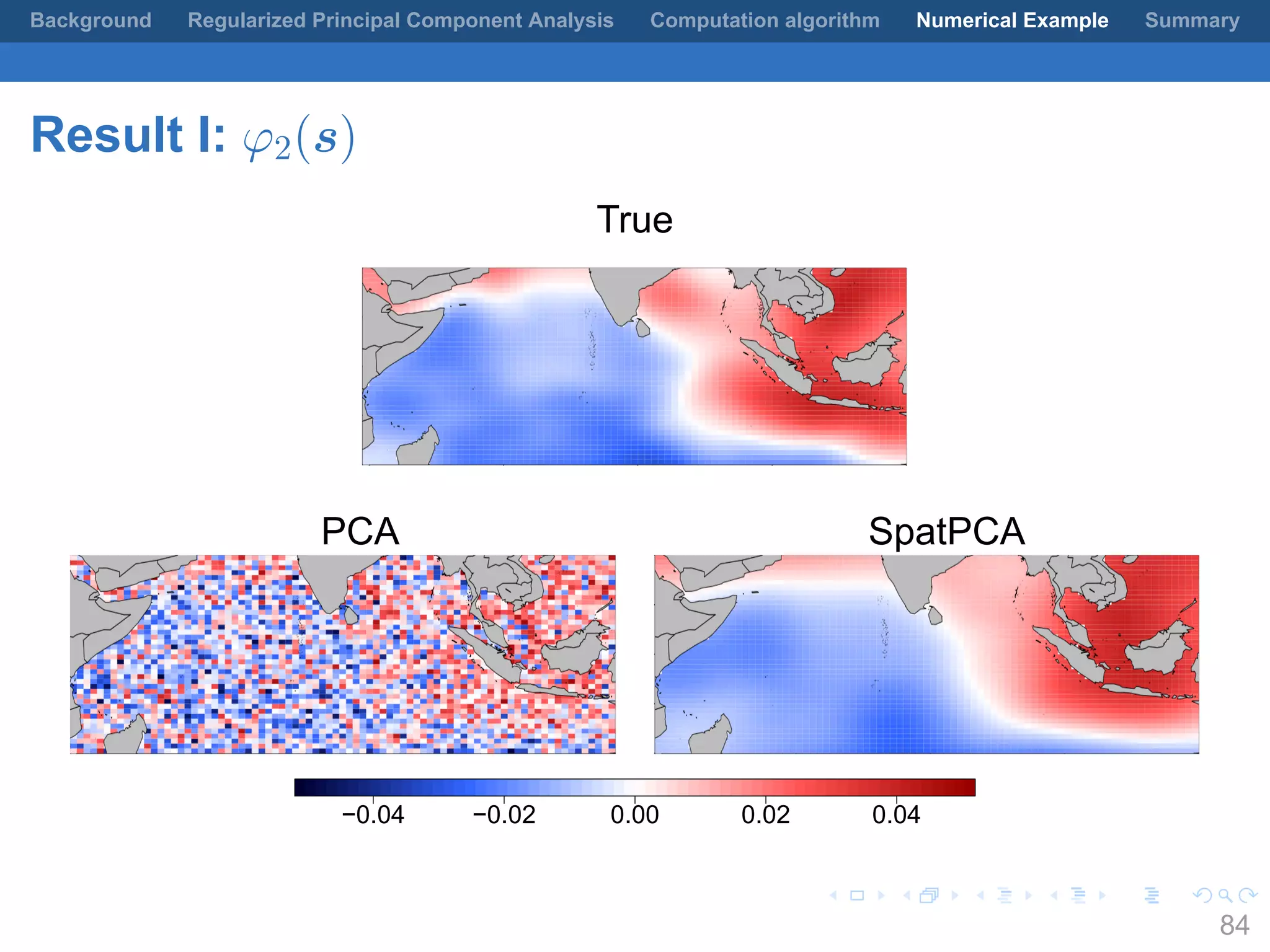
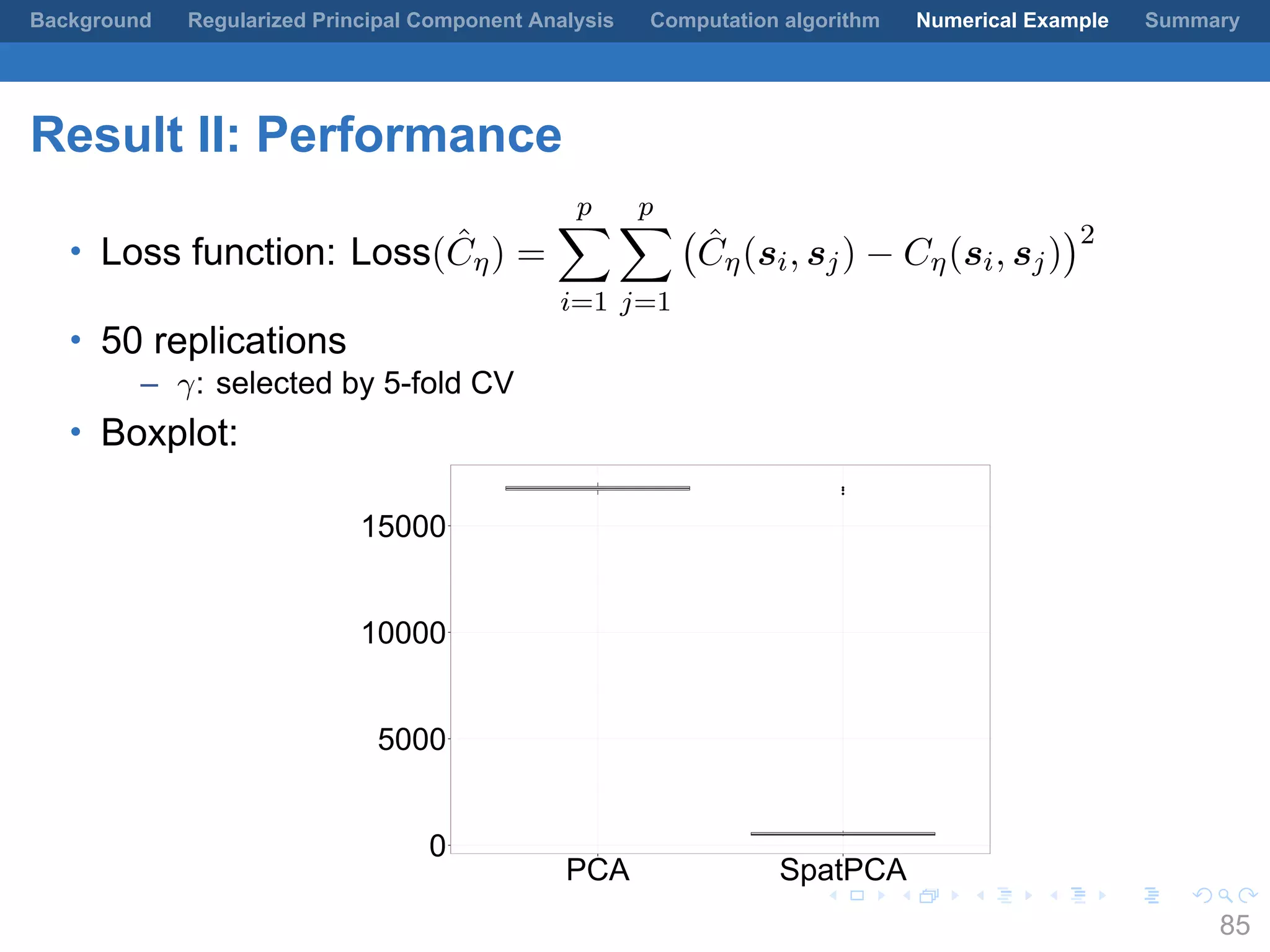
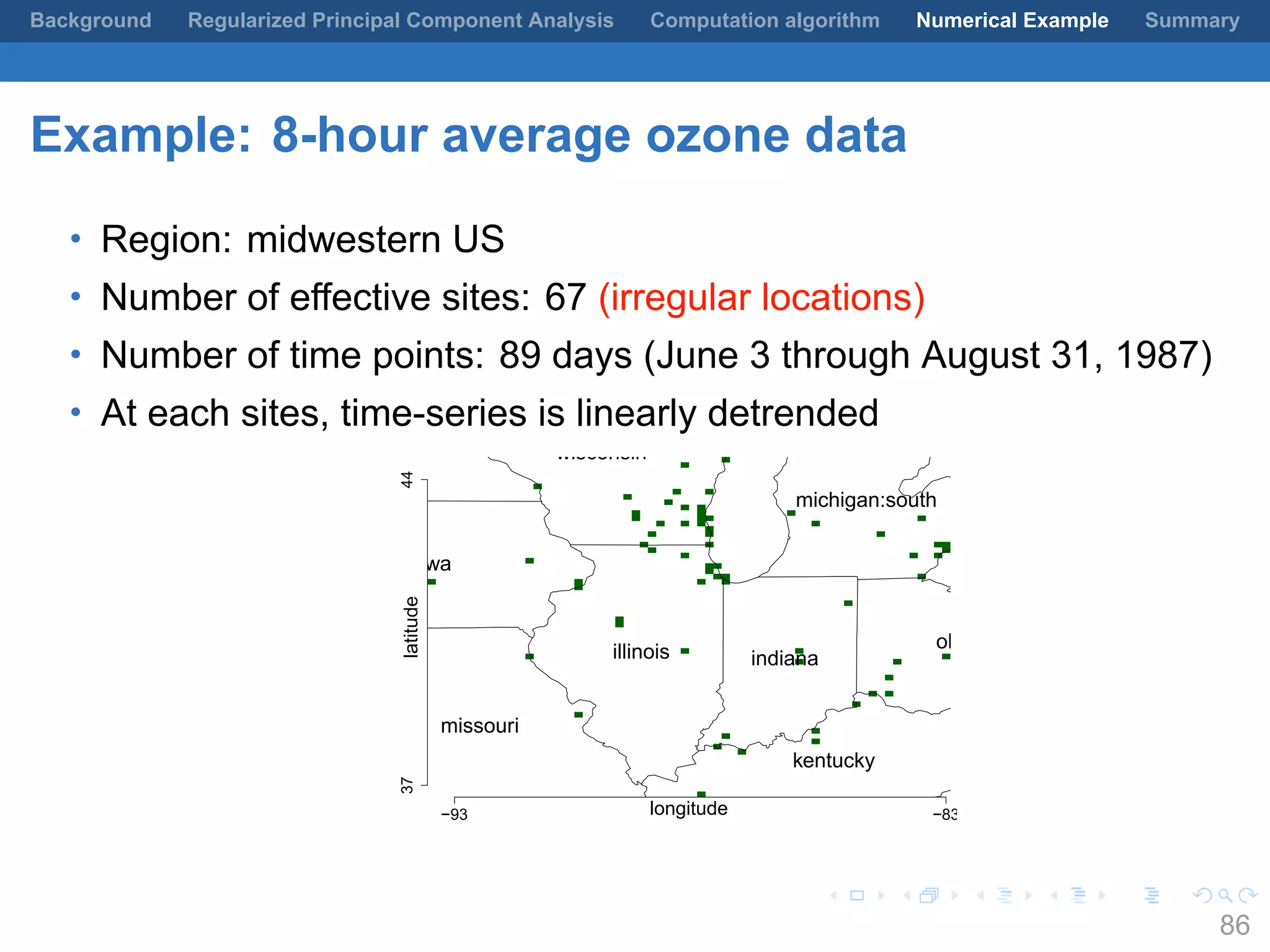
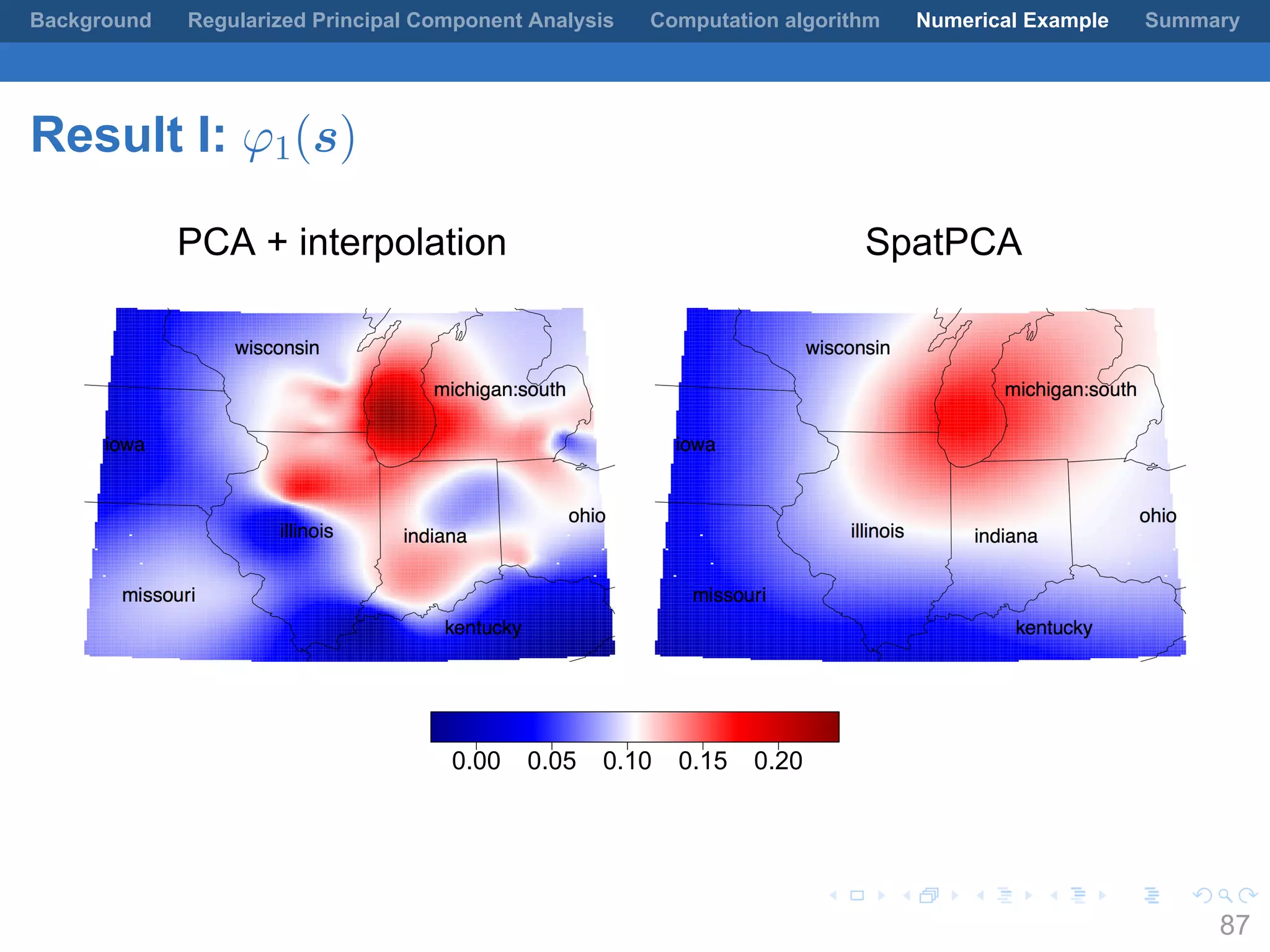
This document presents a method for regularized principal component analysis (PCA) of spatial data. Standard PCA can produce unstable and noisy patterns when applied to spatial data due to high estimation variability from small sample sizes or large numbers of locations. The proposed regularized PCA incorporates spatial structure, sparsity, and orthogonality of the eigenvectors to enhance interpretability. It formulates a rank-K spatial model for the data and aims to estimate the dominant spatial patterns represented by orthogonal functions through regularized PCA.