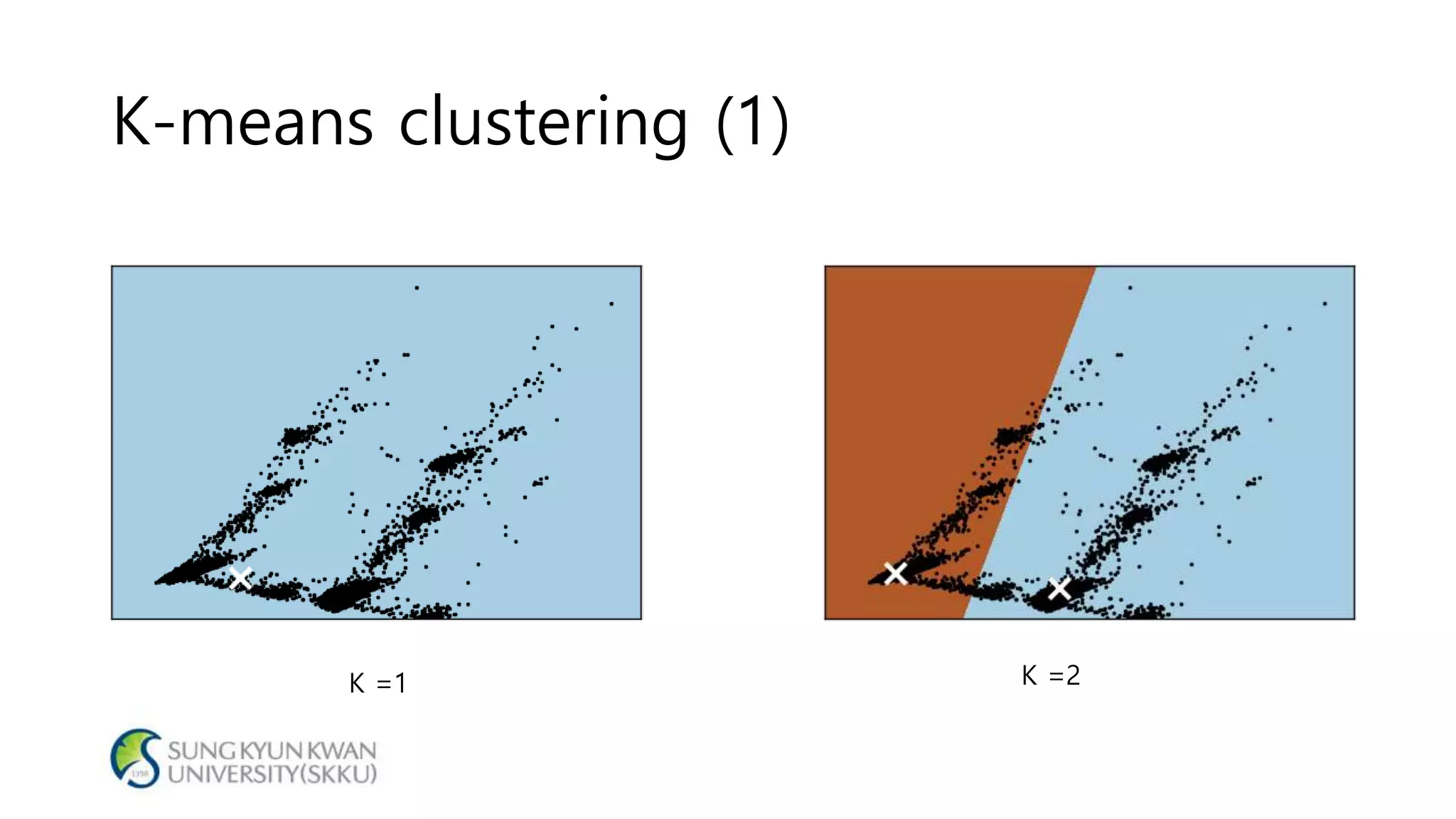
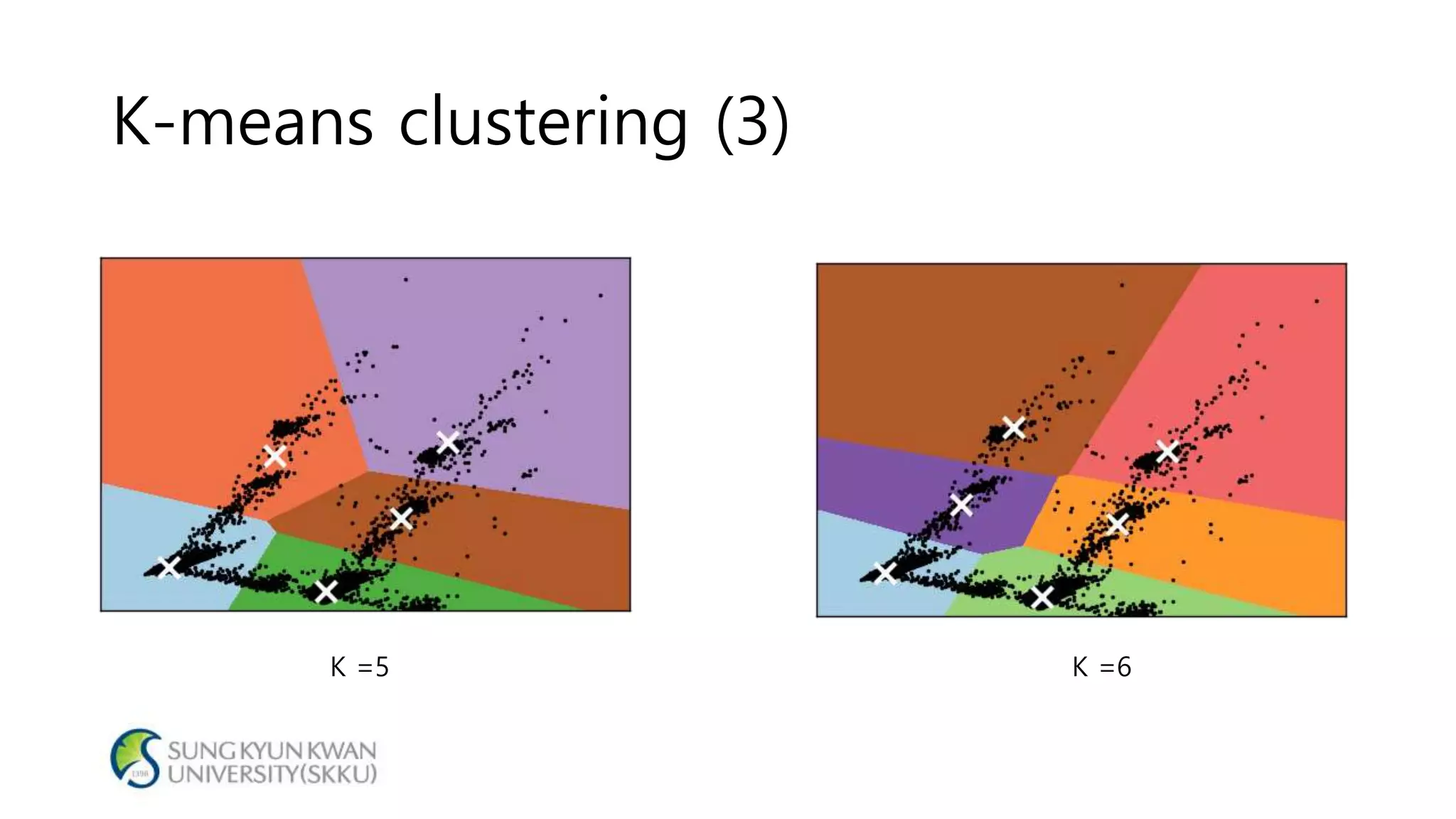
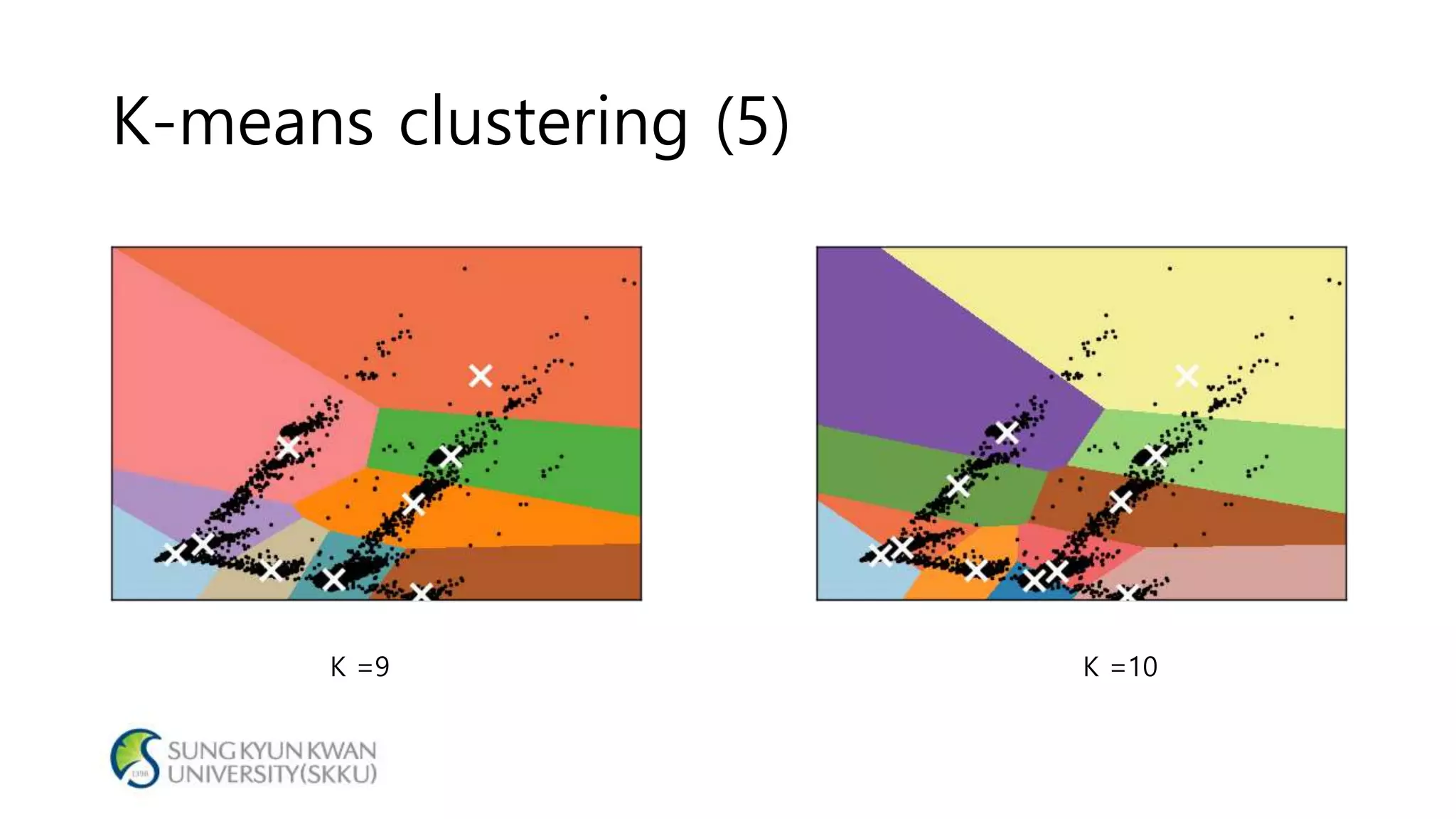
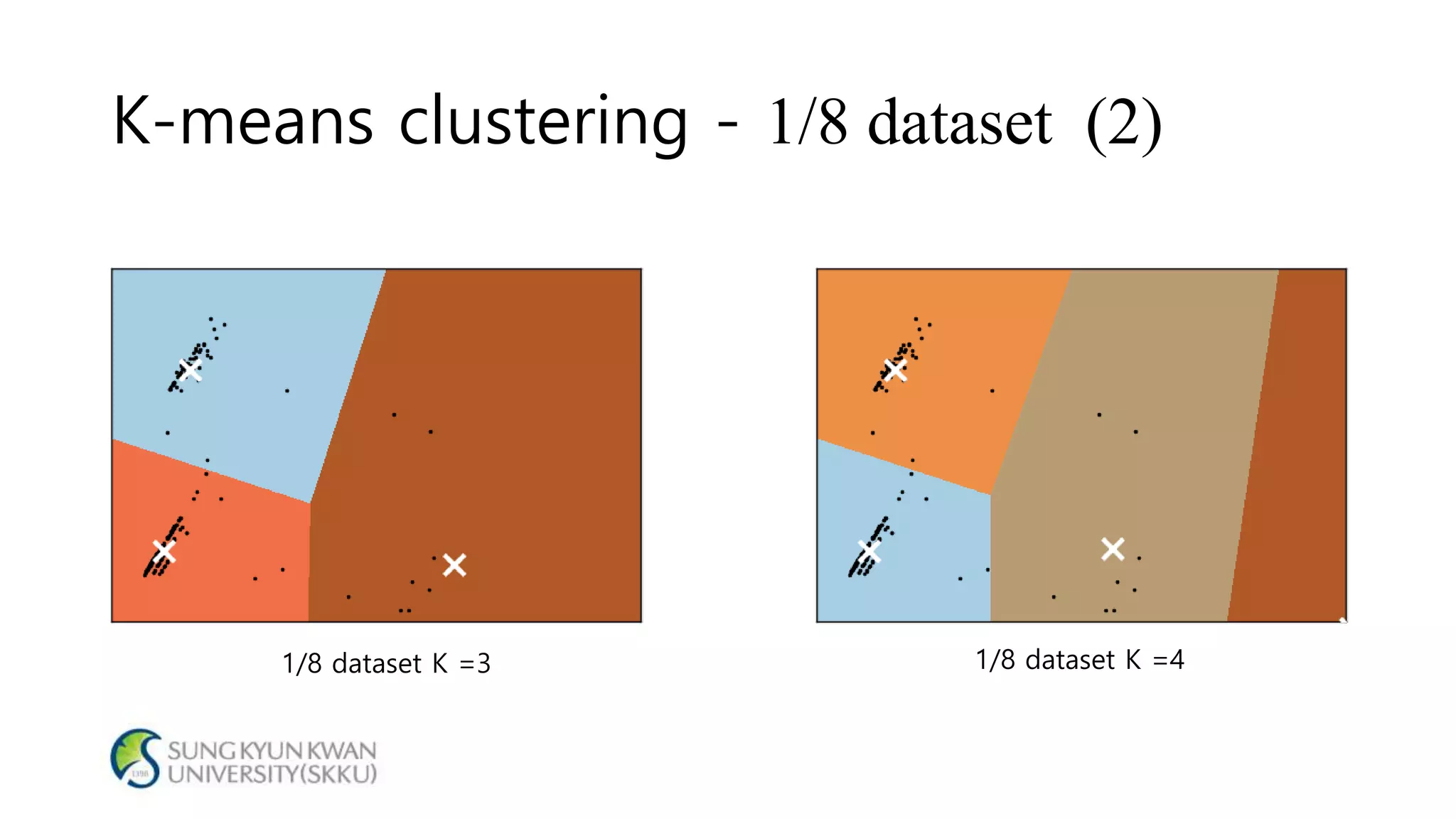
- The document analyzes electricity consumption at home using the K-means clustering algorithm on a dataset and with 1/8 of the original dataset.
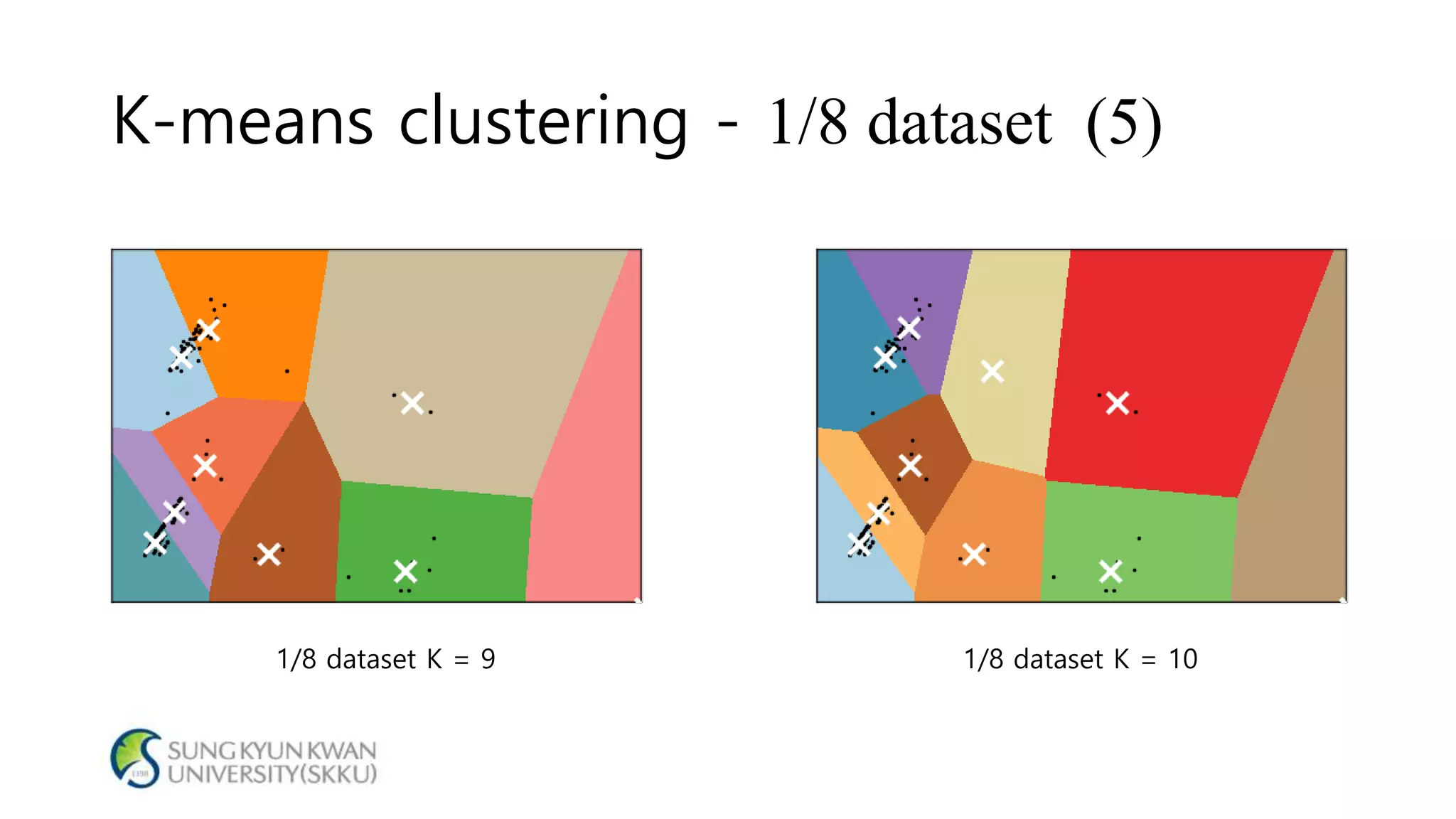
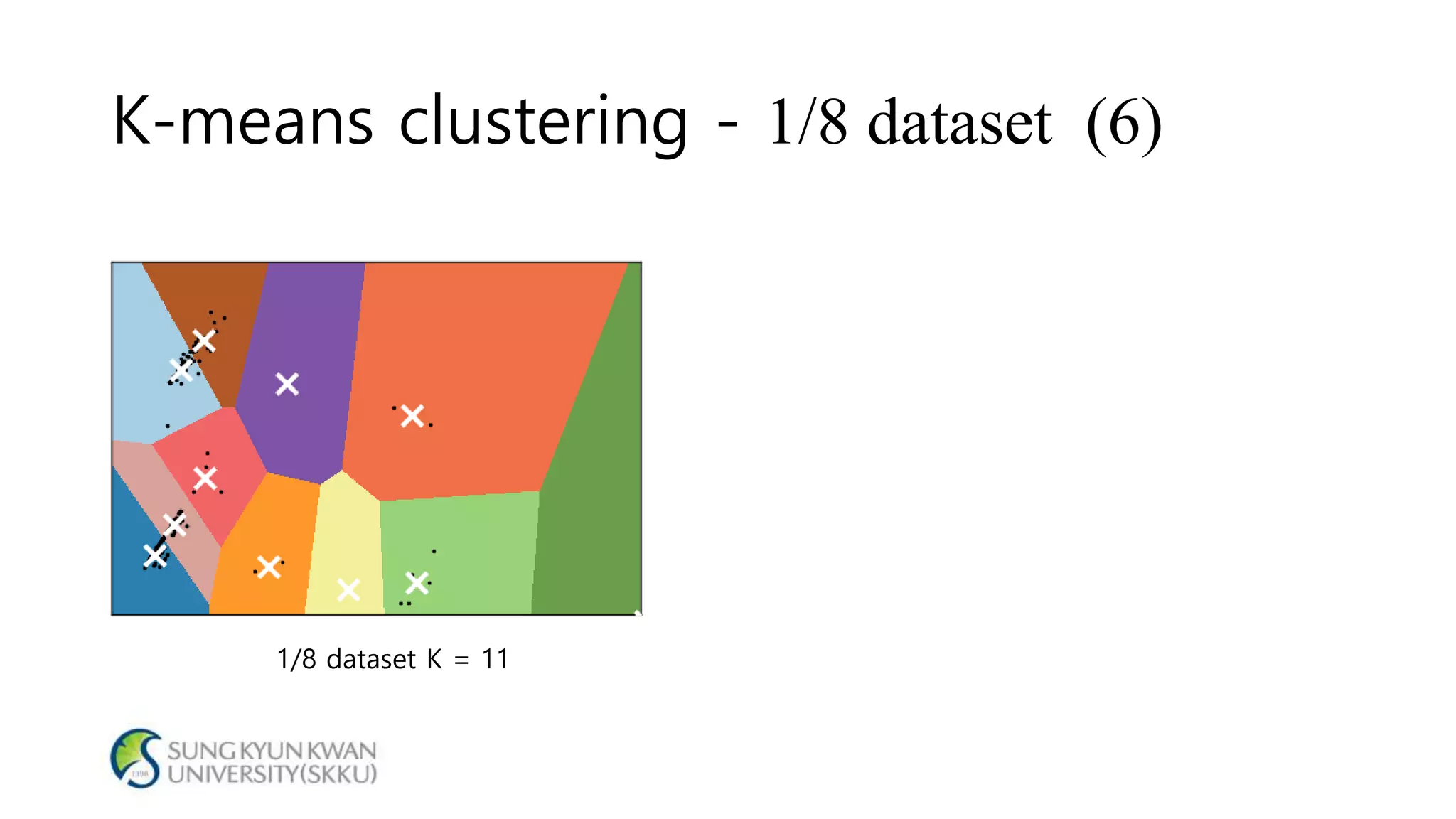
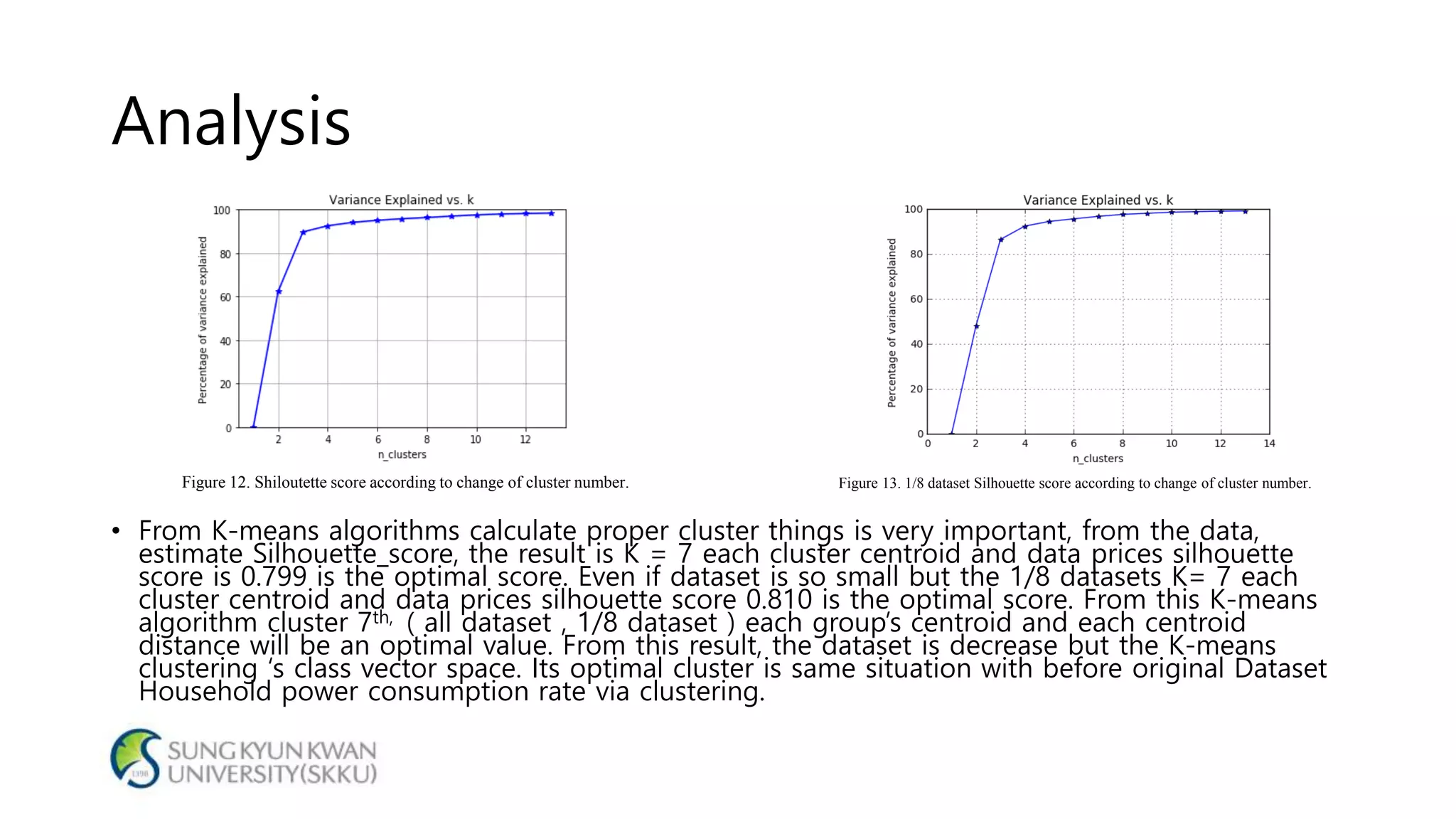
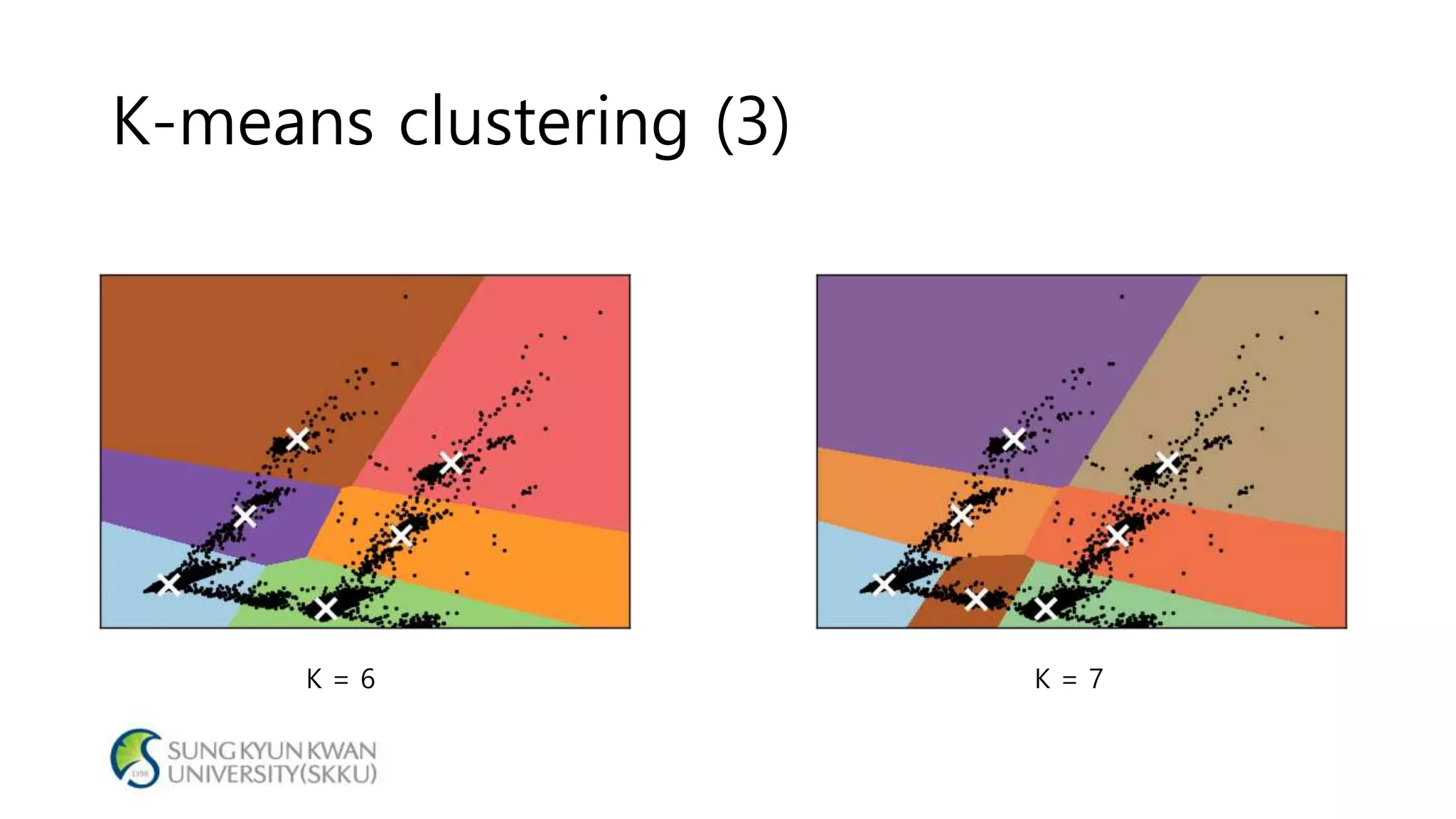
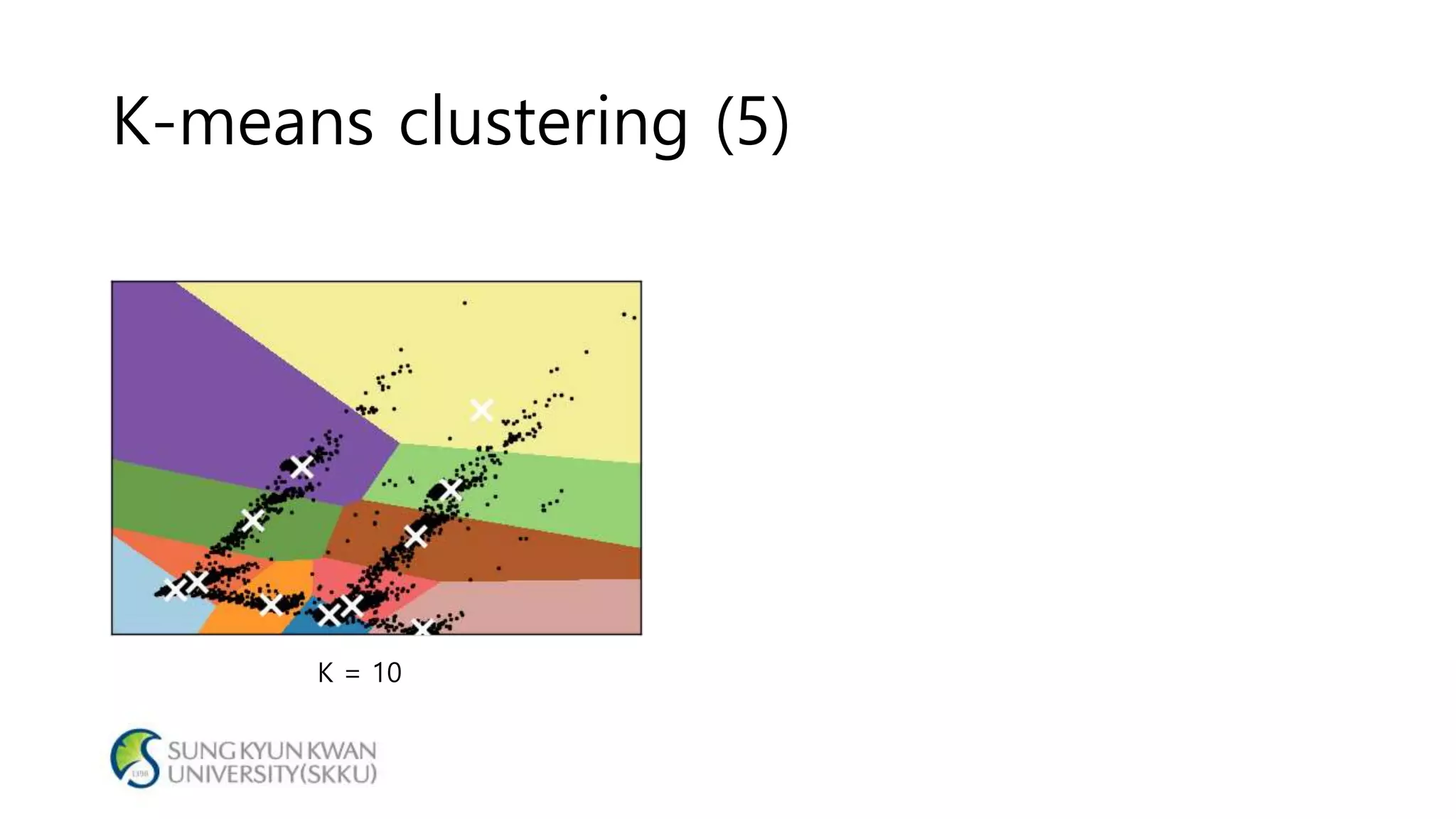
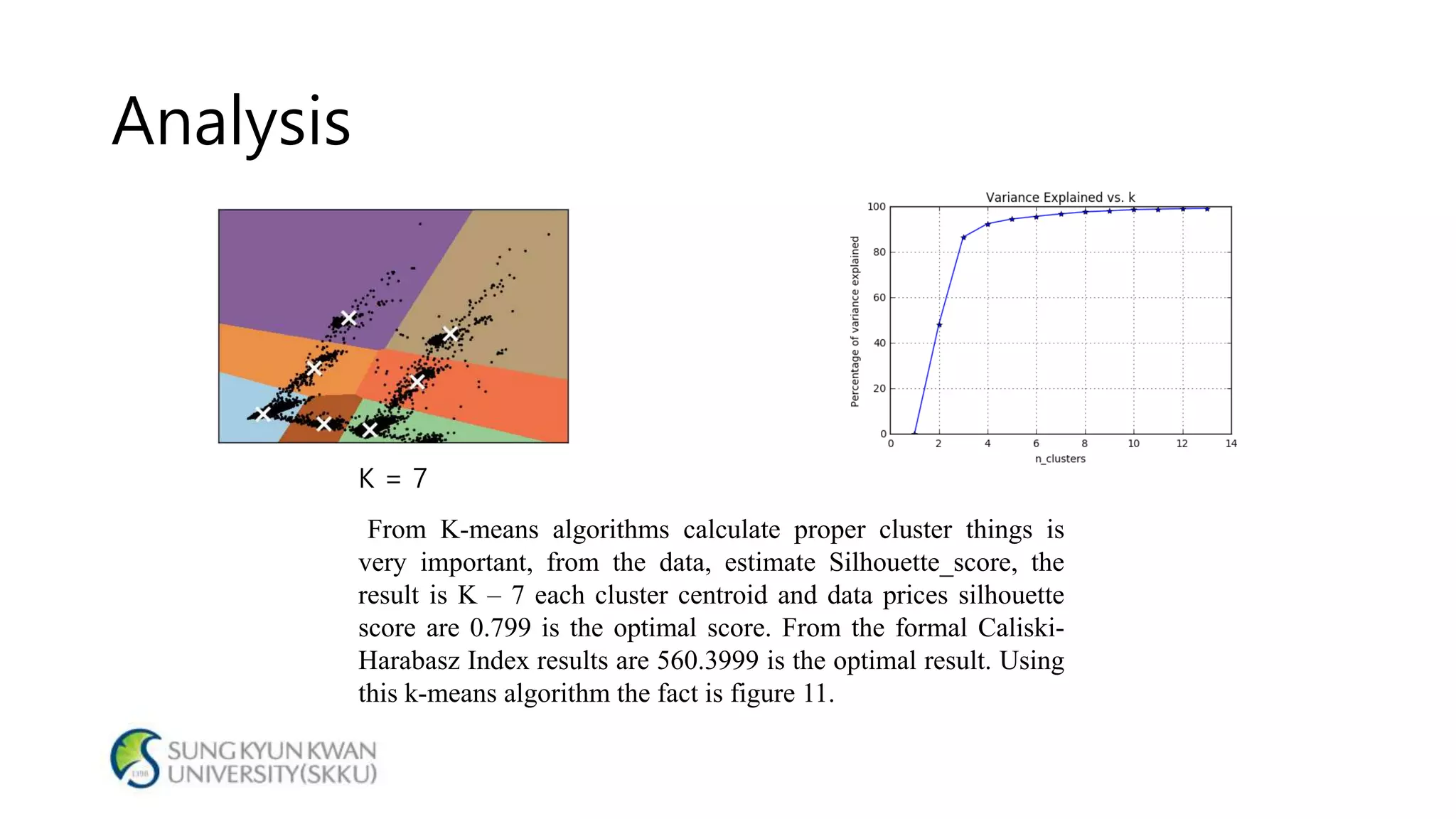
- With the full dataset, the optimal number of clusters was found to be 7, with a silhouette score of 0.799. Using 1/8 of the data, the optimal number of clusters was also 7, with a similar silhouette score of 0.810.
- The analysis shows that even with a smaller dataset, the K-means clustering produced similar results to those from the original larger dataset, suggesting the approach could help analyze large datasets more efficiently.










![K-means clustering
• K-means algorithm is one of the clustering methods for
divided, divided is giving the data among the many partitions.
For example, receive data object n, divided data is input data
divided K (≤ n) data, each group consisting of cluster below
equation is the at K-means algorithm when cluster consists of
algorithms using cost function use it [11]
argmin
𝑖 =1
𝑘
𝑥 ∈ 𝑆 𝑖
𝑥 − 𝜇𝑖
2](https://image.slidesharecdn.com/professornawabpresentation20190409rev1-190522073746/75/presentation-2019-04_09_rev1-11-2048.jpg)




![Silhouette score
• Silhouette score is the easy way to in data I each data cluster in
data’s definition an (i) each data is not clustered inner and data’s
definition b(i) silhouette score s(i) is equal to calculate that
s i =
𝑏 𝑖 − 𝑎(𝑖)
max { 𝑎 𝑖 , 𝑏 𝑖 }
• From this calculate s(i) is equal to that function
−1 ≤ s i ≤ 1
• S(i) is the close to 1 is the data I is the correct cluster to each
thing, close to -1 cannot distribute cluster is distributed, from this
paper machine Using the machine learning library scikit-learn in
the house hold power consumption clustering [7].](https://image.slidesharecdn.com/professornawabpresentation20190409rev1-190522073746/75/presentation-2019-04_09_rev1-18-2048.jpg)





![K-means clustering
• K-means clustering
K-means algorithm is one of the clustering methods for divided,
divided is giving the data among the many partitions. For example,
receive data object n, divided data is input data divided K (≤ n)
data, each group consisting of cluster below equation is the at K-
means algorithm when cluster consists of algorithms using cost
function use it [11]
argmin
𝑖 =1
𝑘
𝑥 ∈ 𝑆 𝑖
𝑥 − 𝜇𝑖
2](https://image.slidesharecdn.com/professornawabpresentation20190409rev1-190522073746/75/presentation-2019-04_09_rev1-25-2048.jpg)