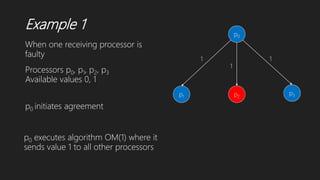
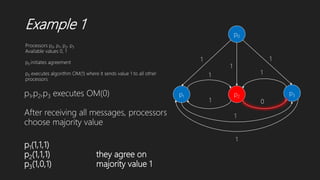
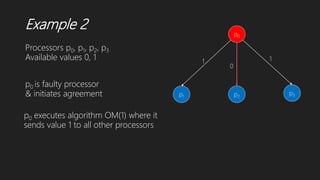
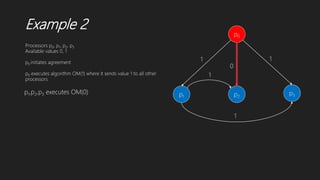
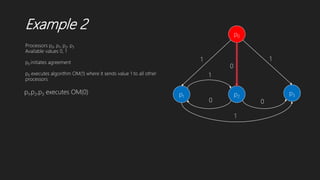
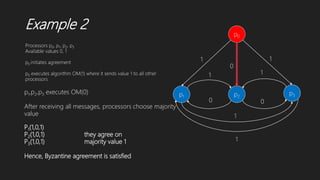
The document summarizes two algorithms for solving the Byzantine agreement problem: 1) Lamport-Shostak-Pease algorithm uses oral messaging to recursively achieve agreement among processors in the presence of faulty processors, as long as the number of faulty processors does not exceed one-third of the total. 2) Dolev et al.'s algorithm does not depend on behavior of faulty processors, requires 2m+3 rounds, and achieves agreement through processors broadcasting messages to confirm values until agreement is reached.

1. Solutions to Byzantine
Agreement Problem
Presentation by Ajay Kharat (BITS Pilani)

2. We studied from last class
-> Faulty processor problem
-> Limitations on number of faulty processors
-> An impossibility result

3. We will be studying about:-
-> Lamport-Shostak-Pease Algorithm
-> Dolev et al.’s Algorithm

4. Lamport-Shostak-Pease Algorithm
Solves Byzantine agreement for 3m+1 or more processors in the presence
of at most m faulty processors
i.e. if there are n processors, faulty processors should not exceed
(n-1)/3
Algorithm is recursively defined, as
• OM(0)
• OM(m), m > 0

5. Oral Messaging (OM)
There must be at least 3m+1 processors to cope up with m faulty
processors by Oral Messaging
What is Oral Messaging?
A Processor has to send messages to other processors
Our Assumptions:-
1. Every message that is sent is delivered correctly
2. The receiver of the message knows who sent it
3. The absence of message can be detected

6. ALGORITHM OM(0)
When there are no faulty processors, achieving agreement is easy
1. The source processor sends its value to every processor
2. Each processor uses the value it receives from the source
Otherwise default value 0

7. ALGORITHM OM(m), m > 0
1. The source processor sends its value to every processor
2. For each i,
let vi be the value processor i receives from the source.
Processor i acts as the new source and initiates Algorithm OM(m-
1) wherein it sends the value vi to each of the n-2 other processors
3. For each i and each j, let vj be the value processor i received from
processor in j in step 2 using Algorithm OM(m-1)
Processor i uses value majority( v1, v2, ..…, vn-1 )

8. What is Majority
If majority of values vi for each processor is
majority( v1,v2,v3,……,vn-1 )
The majority value among the vi if it exists, otherwise the value 0
i.e. a value at which majority of processors agree on.

9. Example 1
Processors p0, p1, p2, p3
Available values 0, 1
p2p1
p0
p3
1
1
1
p0 initiates agreement
p0 executes algorithm OM(1) where it
sends value 1 to all other processors
When one receiving processor is
faulty

10. Example 1
Processors p0, p1, p2, p3
Available values 0, 1
p0 initiates agreement
p0 executes algorithm OM(1) where it sends value 1 to all other
processors
p2p1
p0
p3
1
1
1
1
1
1
0
p1,p2,p3 executes OM(0)
After receiving all messages, processors
choose majority value
p1(1,1,1)
p2(1,1,1) they agree on
p3(1,0,1) majority value 1
1
1

11. Example 2
Processors p0, p1, p2, p3
Available values 0, 1
p2p1
p0
p3
1
0
1
p0 is faulty processor
& initiates agreement
p0 executes algorithm OM(1) where it
sends value 1 to all other processors

12. Example 2
Processors p0, p1, p2, p3
Available values 0, 1
p0 initiates agreement
p0 executes algorithm OM(1) where it sends value 1 to all other
processors
p2p1
p0
p3
1
0
1
1
p1,p2,p3 executes OM(0)
1

13. Example 2
Processors p0, p1, p2, p3
Available values 0, 1
p0 initiates agreement
p0 executes algorithm OM(1) where it sends value 1 to all other
processors
p2p1
p0
p3
1
0
1
1
0 0
p1,p2,p3 executes OM(0)
1

14. Example 2
Processors p0, p1, p2, p3
Available values 0, 1
p0 initiates agreement
p0 executes algorithm OM(1) where it sends value 1 to all other
processors
p2p1
p0
p3
1
0
1
1
0
1
0
p1,p2,p3 executes OM(0)
After receiving all messages, processors choose majority
value
P1(1,0,1)
P2(1,0,1) they agree on
P3(1,0,1) majority value 1
Hence, Byzantine agreement is satisfied
1
1

15. Dolev et al.’s Algorithm
Motivation behind Dolev et al.’s Algorithm?
• Does not depend on behavior of faulty processor
• Requires 2m+3 rounds
• No Authentication required
• It is polynomial time algorithm for reaching Byzantine
Agreement

16. Dolev et al.’s Algorithm
Our Assumptions
• Topology of network is known
• Algorithm is synchronous i.e. time of each round is known
• Without authentication immediate sender of message can be identified
• No solution if the upper bound of faulty processor exceeds
i.e. 1/3 of the processes

17. Dolev et al.’s Algorithm
• m is number of faulty processors
• Two thresholds :-
LOW = m + 1, HIGH = 2m + 1
• LOW is any subset of atleast one nonfaulty processors
(Used to support assertion)
• HIGH is any subset of atleast m + 1 nonfaulty processors
(Used to confirm assertion)
• Two Types of Message:-
• “*” Message and a message containing name of processor

18. Dolev et al.’s Algorithm
• What is * Message?
“*” denotes sender is sending value 1
• What is named message?
denotes sender of the message received a “*” from a named processor.
Every processor keeps a record of all messages it has received.
Processor j is direct supporter of k if j directly receives “*” from k.
When a nonfaulty processor j directly receives “*” from processor k, it sends message “k” to all
other processors
When processor i receives message “k” from processor j, it adds j into Wi
x because
j is a witness to message “k”
Wi
x is set of processors (witness) that have sent message x to processor i.

19. Dolev et al.’s Algorithm
k
j
* k
k
k
i
Wi
k [ j,…..,]
Witness for k message is j
Processor j is direct supporter of k if j directly receives “*” from k.
When a nonfaulty processor j directly receives “*” from
processor k, it sends message “k” to all other processors
When processor i receives message “k” from processor j, it adds
j into Wi
k because j is a witness to message “k”
Wi
k is set of processors (witness) that have sent message k to
processor i.
Processor i is indirect supporter of processor j
if |Wi
k|>= LOW
Processor i confirms processor j
if |Wi
k|>= HIGH

20. Dolev et al.’s Algorithm
Four rules of operation:
1. In first round, the source broadcasts its value to all other processors
2. In round k > 1, processor broadcasts name of all processor for which it is either
direct or indirect supporter.
if it not yet initiated in previous round, it will broadcast “*” message
3. If processor confirms HIGH number of processor, it commits to a value of 1.
4. After round 2m+3, if the value 1 is committed, the processor agree on 1;
Otherwise they agree on 0

21. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1]
W1 []
W2 []
W3 []
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* *
Round 1
P1 initiates and sends *

22. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,3]
W1 []
W2 []
W3 []
W4 []
W* [1,3]
W1 [3]
W2 []
W3 []
W4 []
W* [1,3]
W1 []
W2 []
W3 []
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
Round 1 Status
Round 2

23. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 []
W2 []
W3 []
W4 []
W* [1,2,3]
W1 [3]
W2 []
W3 []
W4 []
W* [1,2,3]
W1 [2]
W2 []
W3 []
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
Round 1 Status
Round 2

24. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 [2]
W2 []
W3 [2]
W4 []
W* [1,2,3]
W1 [2,3]
W2 []
W3 [2]
W4 []
W* [1,2,3]
W1 [2]
W2 []
W3 [2]
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
3,1
3,1
Round 2 Status
Round 3

25. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 [2,,3]
W2 [3]
W3 [2]
W4 []
W* [1,2,3]
W1 [2,3]
W2 [3]
W3 [2]
W4 []
W* [1,2,3]
W1 [2,3]
W2 []
W3 [2]
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
3,1
3,1
2,1 2,1
Round 2 Status
Round 3

26. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 [2,,3]
W2 [3]
W3 [2]
W4 []
W* [1,2,3]
W1 [2,3]
W2 [3]
W3 [1,2]
W4 []
W* [1,2,3]
W1 [2,3]
W2 [1]
W3 [2]
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
3,1
3,1
2,1 2,12
3
Round 2 Status
Round 3

27. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 [1,2,3]
W2 [1,3]
W3 [1,2]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1,3]
W3 [1,2]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1]
W3 [1,2]
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
3,1
3,1
2,1 2,12
31,2,3
1,2,3
Round 3 Status
Round 4

28. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1,2]
W3 [1,2]
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
3,1
3,1
2,1 2,12
31,2,3
1,2,3 1,2,3
1,2,3
Round 3 Status
Round 4

29. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2,3]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2,3]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2,3]
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
3,1
3,1
2,1 2,12
31,2,3
1,2,3 1,2,3
1,2,3
1,2,3
1,2,3
Round 3 Status
Round 4

30. Dolev et al.’s Algorithm
p1 p2
p3 p4
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2,3]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2,3]
W4 []
W* [1,2,3]
W1 [1,2,3]
W2 [1,2,3]
W3 [1,2,3]
W4 []
W* [1]
W1 []
W2 []
W3 []
W4 []
*
* **,1
*
*
*,1
3,1
3,1
2,1 2,12
31,2,3
1,2,3 1,2,3
1,2,3
1,2,3
1,2,3
An Agreement is reached in 4 rounds

31. Papers Referred
An Efficient Algorithm for Byzantine Agreement without Authentication
https://www.sciencedirect.com/science/article/pii/S0019995882907768
The Byzantine Generals Problem
https://people.eecs.berkeley.edu/~luca/cs174/byzantine.pdf