solution-manual-3rd-ed-metal-forming-mechanics-and-metallurgy

1. Chapter 9
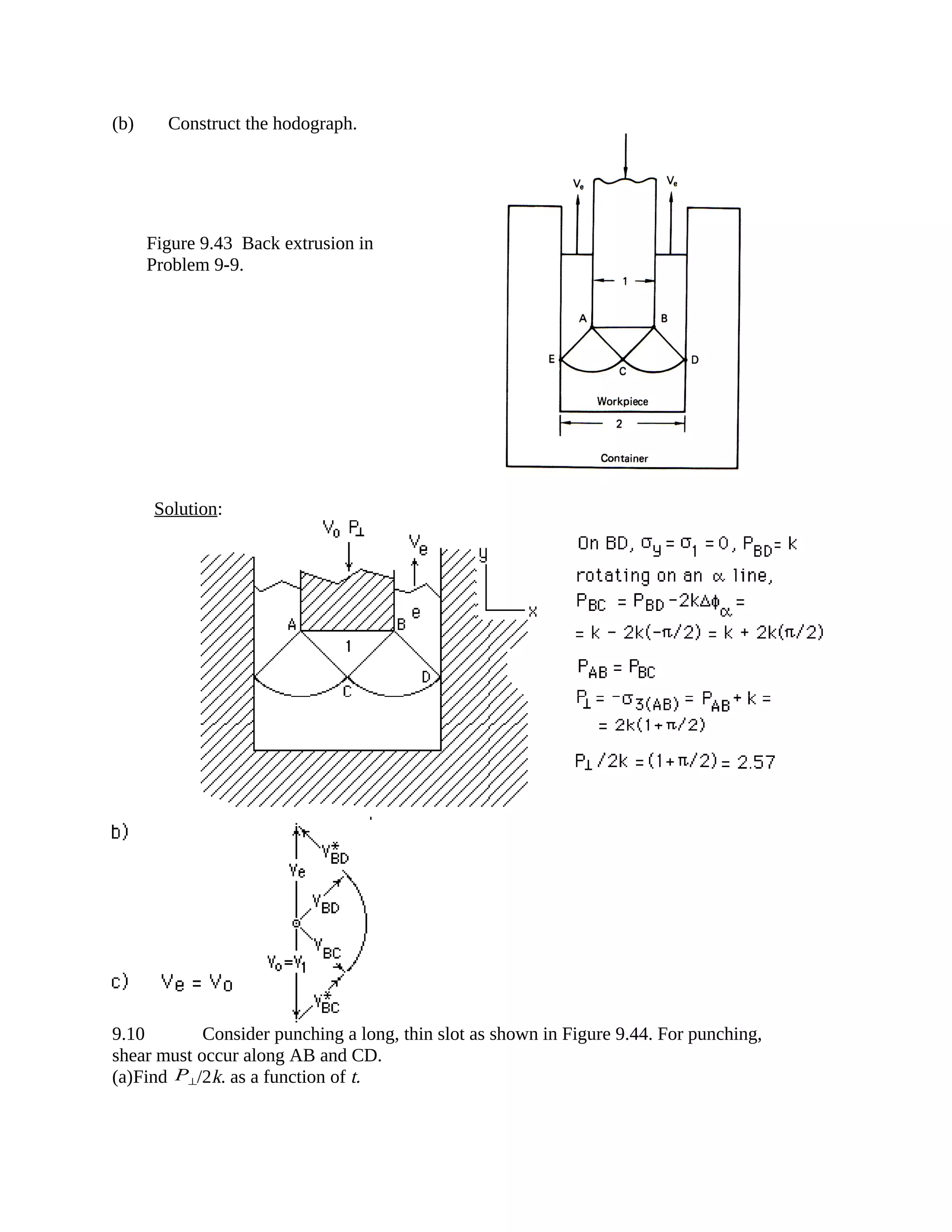
9-1 Using the slip-line field in Figure 9.8 for frictionless indentation it was found that
P⊥/2k = 2.57. Figure 9.35 shows an alternate field for the same problem proposed by Hill.
(a) Find P⊥/2k for this field.
(b) Construct the hodograph.
(c) What percent of the energy is expended along
lines of intense shear?
Figure 9.35 Slip-line field for plane-strain indentation.
Solution: a)Along ED, σ1 = 0, σ2 = -k, Along EC σ2 = -k, DCFBA is an α-line so in
triangle ABE σ2 = -k +2k∆φ = -k +2k(-π/2) = -k(1+π). σ3 = σ2 -k = P ⊥ . P ⊥ /2k =
1+π/2 = 2.57.
b)
Vp = 1
VAE
V*AB
VF
V*CD
=1,
Intense shear occurs along ABFCD. Note that along BE and EC, the deformation is
gradual.. Letting AE=1, AB=1/√2= BE=CD, BC=(π/2)BE, V*AB = Vp√2 =
V*BC = V*CD so the rate of energy dissipation on these lines is
k( ABV*AB + BCV*BC + CDV*CD) or k[(1/√2)(√2) + π((1/√2)(√2) +(1/√2)
(√2)]Vp. = (2 + π/2)k = 3.57k.

2. The total rate of energy dissipation from (a) is 5.14k so the energy dissipation from
theses lines is 3.57/5.14 = 69.5%
9-2. Figure 9.36 shows a slip-line field with a frictionless punch. Construct the
hodograph and find P⊥/2k for this field.
Solution:
Vp
V* GO
VG
VF
V* DE =VE
9-3. Plane-strain compression of a hexagonal rod is shown in Figure 9.37
together with a possible slip line field.
(a) Determine whether this field or penetrating deformation will occur.
(b) Find P⊥/2k.
Figure 9.36 Slip-line field
for Problem 9-2.
Figure 9.37. Possible slip-line field for
Problem 9-3.

3. Solution:
σ2A = -k + 2k(-π/6) = -k(1 + π/3) = σ2BC
σ3BC = σ2BC - k = -P = -2k(1 + π/6) so P⊥/2k = 1 + π/6 = 1.523
On the other hand, for penetrating deformation, P⊥/2k = 1.15 according to Fig. 9-20, which
is lower and therefore appropriate
b) For von Mises, 2k = 2Y/√3 so P^= 2.25,000/√3 = 33,200 psi
9-4 Figure 9.38 is the slip-line field for plane-strain wedge indentation. For the
volume of the side mounds to equal the volume displaced, the angle ψ must be
related to θ by cos(2θ-ψ) = cosψ/(1 + sinψ). Determine F/x in terms of 2k for θ =
120°.

4. Figure 9.38 Slip-line field for plane-strain wedge indentation.
Solution: a)
Substituting 2θ = 120o into cos(2θ - ψ) = cos ψ/(1+siny), and solving by trial
and error, ψ = 50.84o = 0.887 radians. Starting on the left-hand side, at the surface σ1 = 0,
so P = k. Now rotating on a β-line through ∆φβ = +0.887, the pressure in the D next to
indenter is
P∆ = k + 2k(0.887); P⊥ = P∆ + k = 2k(1.887). Let the length of contact between indenter
and material be 1, then F⊥ = P⊥, Fx = F⊥ sin60 = P⊥sin60, σx = Fx/sin60 = P⊥ =
2k(1.887), σx/2k = 1.887
9-5. Figure 9.39 shows the slip-line field for a 2:1 reduction by indirect or
backward frictionless extrusion.
(a) Determine P⊥/2k..
(b) Construct a hodograph for the lower half of the field.
(c) Find V*AD/V0.
(d) What percent of the energy is expended by the gradual deformation in the
centered fans?
Solution:a) By inspection, A'B'CD is an α-line and CD and A'D' are β-lines.
Along CD', σx = 0 so PCD' = k, rotating on a-lines -π/2 from CD' to A'D',
PA'D' = PCD' -2k(-π/2) = k +2k(π/2)
This is the pressure in triangle A'E'D', so Pext = P⊥ = PA'D' + k = 2k(1+π/2)
pext/2k = 2.57
c) V*AD = V*CD = (√2/2)Vo = √2/2 = .707
Figure 9.39 Slip-line field for
the indirect extrusion of
Problem 9-5.

5. d) rate of energy expenditure along AD and CD = k( ADV*AD+ CDV*CD) = 2k AD
V*AD = 2k(√√2)(√2/2)] = 2k
rate of energy expenditure along arc ABC = k ABCV*ABC
arc length ABC= √2π/2), the velocity discontinuity along this arc V*ABC = V*AD = (√2/2)Vo
= √2/2, so rate of energy = kπ/2 =2k(π/4)
total rate of work = PextVox1 = 2k(1+π/2)
Thefraction expended on lines AD, CD & arc ABC = (1+π/4)/(1+π/2)= 69.4%
The rest is expended in fan = (π/4)/(1+π/2) = 30.6%
9-6 Fig. 9.40 shows the slip-line field for the 3:1 frictionless extrusion. Find P⊥
/2k and η.
Solution:
This is one of the special fields covered in sect 9-6 for which sinα = r/[2(1-r)]. (Here α =
90o=π/2 so sinα = 1 and r = 2/3. For these fields Pext/(2k) = r(1+α) = (2/3)(1+ π/2) = 1.714
η = wi/wa = 2kε/Pext = 2kε/[2kr(1+α)] = ln3/[(2/3)(1+ π/2)] = η = 64.1%
Note this problem can also be solved by realizing that along PCD = k, and rotating on an α-line
through ∆φα = -π/2, PABD = k + 2k(π/2)
P⊥ = PABD + k = 2k(1+π/2), 3Pext = 2P^, so Pext/2k = (2/3)(1+π/2) etc.
9-7 Indentation of a step on a semi-infinite hill is shown in Figure 9.41. Show that this
field is not possible and draw a correct field
Figure 9.40 The slip-line
field for the 3:1 frictionless
extrusion in Problem 9-6.

6. Solution: σ1FG = 0, σ2FGE = -k, FEDA is an α-line.
a) starting from the right side of the field, σ2D = σ2E + 2k∆φDE = -k + 2k(-φR) (clockwise) so
σ2D = -k -2kφR. Starting from the left side of the field, σ1AB = 0,σ2ABC = -k, BCDG is a β-line.
σ2D = σ2C - 2k∆φDC = -k - 2k(φL) (counterclockwise) so σ2D = -k -2kφL
Since φR > φL, the value of σ2D calculated from the two fields is different. The full field cannot
be correct.
b) Simply use the portion GDCBA which gives the lower value of P/(2k)
9-8 What is the highest level of hydrostatic tension, expressed as σ2/2k, that can be
induced by two opposing flat indenters as shown in Figure 9.42?
Solution: The highest midplane tensile stress occurs in the field with the highest H/L for
which deformation penetrates. From fig 9-20, H/L = 8.75. For this field P⊥/2k = (1 + π/2). The
value of P in the triangle below the indentor is P⊥ - k. The field corresponds to a centered fan with
−∆φα = + ∆φβ = 5π/12 + (8.75-8.16)/(12.37-8.16)(π/12) = 5.13(π/12)
At the centerline, P = P⊥ -k -2k(∆φα+ Dfb) = (1 + π/2)(2k) -k -2k(2x5.13)(π/12)
P/2k = (1 + π/2) - .5 - (2x5.13)(π/12) = -.615, σ = +0.615
9-9 Consider the back extrusion in Figure 9.43. Assume frictionless conditions.
(a) Find P⊥/2k.
Figure 9.41 An incorrect field
for indentation on a semi-
infinite hill
Figure 9.42 Indentation by two
opposing flat indenters.

7. (b) Construct the hodograph.
Solution:
9.10 Consider punching a long, thin slot as shown in Figure 9.44. For punching,
shear must occur along AB and CD.
(a)Find P⊥/2k. as a function of t.
Figure 9.43 Back extrusion in
Problem 9-9.

8. (b) If the ratio of t/w is too great, an attempt to punch will result in a plane-
strain hardness indentation. What is the largest ratio of t/w for which a slot can be
punched?
(c) Consider punching a circular hole of diameter, d. Assume that for a can be
punched
Solution: a) The area of shear = 2lt, The internal work rate is ÝW int = k ≥ 2lt ≥ Vp. The external work
rate is ÝW ext= P ≥ wl ≥Vp. Equating, P ≥ wl ≥ Vp = k≥2lt≥Vp, P/(2k) = t/w.
b) Hardness indentation will occur if P/(2k) = 1 +p/2 = 2.57. Therefore since P/(2k) = t/w, if t/w >
2.57, a hardness indentation will occur instead of punching of the slot.
c) Now the upper-bound gives Wint = kpdtVp = Wext= Pp(d2/4)Vp. Therefore, P/
(2k) = 2t/d. Equating with P/(2k) = 3, 2t/d = 3; d/t = 2/3. NOTE : This is a minimum value
of d/t for hole punching, not a maximum as implied
9-11 Deeply notched tensile specimen much longer than its width and very deep in the
direction normal to the drawing is shown in Figure 9.45. Calculate σx/2k for the field
where σx = Fx/tn.
``
Figure 9.45 Deeply-notched tensile specimen for Problem 9-11.
Solution: First label the a and b-lines as shown . This is easily done at point C where obviously the
most tensile direction (and therefore the 1 axis) is vertical.
Figure 9.44 Slot punching.

9. In triangle ABF, σy = σ3 = 0. σ2(FB) = k. Moving along a β line to FC, σ2(FC) = σ2(FB) -
2k(∆φβ) = k - 2k(-π/2)Every where within region CFIG, σ2 is the same and σ1 = σ2 + k = 2k +
2k(π/2) = 2k(1+ π/2).
The stress σ = F/x = σ1= 2k(1+ pπ/2), so σ/2k = (1+ π/2) = 2.57
Note that half of this field is exactly the same as the field for plane- strain indentation except that
all of the stresses are tensile here instead of compressive. Our answer for the stress here is the
same as for the indentation problem (1+ π/2 = 2.57) except that the stress is tensile.
9-12 Consider a plane-strain tension test on the notched specimen in Figure 9-46.
Figure 9.46 Notched tensile specimen for Problem 9-12.
Solution: At the surface, the stress normal to the surface, σ3 =0, so σ2 = k.
Rotating 45o = π/4 to the center, σ2 = k + 2k(π/4). and here σ1 = σ2 + k = 2k(1+π/4).
The stress is the same everywhere along a cut through the center so σx = σ1 = 2k(1+π/4).
σx/2k = (1+π/4) = 1.785
9-13 If the notches in Problem 9-12 are too shallow (i.e. to/tn is too small) the specimen
may deform by shear between the base of one notch and the opposite side as shown in
Figure 9.47. What ratio of to/tn is needed to prevent this?

10. Solution: From problem 9-12, the value of σx necessary to operate the field is 1.785, or σx = =
1.785(2k) = 3.571k.
Alternatively, shear could occur on a 45o plane from the base of the notch to the opposite surface. The
shear stress on such a plane,
τ = Fxcos45/{(1/cos45)(tn +to)/2} = (1/2)σxtn /[(tn +to)/2] = σxtn /(tn + to).
Shear will occur on such a plane when τ = k, so for shear
k = σxtn/(tn + to) or σx = k(tn + to)/tn = k(1+ to/tn)
For the field to operate instead of shear, 3.571k < k(1+ to/tn), or to/tn > 2.571
9-14 Figure 9.48 shows the appropriate slip-line field for either frictionless plane-
strain drawing or extrusion where r = 0.0760 and α = 15°.
a. Find the level of σ2 at point 4,5 for extrusion.
b. Find the level of σ2 at point 4,5 for drawing.
c. How might the product depend on whether this is an extrusion or a drawing?
Figure 9.47 Alternate mode of
failure for a notched tensile bar
if to/tn isn’t large enough. For
Problem 9-13.

11. Solution: a) An x-direction force balance gives Pext
.1 = P⊥(r/sin15)sin15 = P⊥r.
If for α = 15 and r = 0.076, Pext = 2k(0.178), P⊥ = 2k(0.178/( 0.076) = 2.342(2k)
Then P in ∆ABO,O = P^- k = ( 2.342 -.5)(2k) = 1.842(2k)
Rotating by ∆φα = + 5π/12 and Dfb= -4 π/12 to the centerline,
P4,5 = 1.842(2k) - (2k)(9π/12) = -0.514(2k) or s2 = +0.514(2k)
(b) If this were a drawing operation the drawing stress would be σd/2k = 2k(0.178) and an x-
direction force balance gives σd(1-r) = P⊥r, so P⊥= σd(1-r)/r = 2k(0.178)(1- .070)/.076 = 2.164(2k).
Now P in ∆ABO,O = 1.646(2k) and moving to the centerline,
P = 1.646(2k) - (2k)(9π/12) = -0.710(2k) or σ2 = 0.710(2k).
(c) The higher hydrostatic tension at centerline in drawing would cause more centerline porosity
and internal cracks, lowering the toughness.
9.15 Figure 9.49 shows two slip-line fields for the compression of a long bar with an
octagonal cross section. Which field is appropriate? Justify your answer.
Figure 9.48 Slip-line field for
Problem 9-14.

12. Solution: For an octagon the value of h/L = 1 + 2√2/2 = 1 + √2 = 2.414. For penetrating flow with
h/L = 2.4, Figure 9-19 indicates that P⊥/(2k) = about 1.4.The non-penetrating flow field is very
similar to the hardness indentation except that the centered fans are now π/4 instead of π/2.
Consequently the pressure required is P⊥/(2k) = 1 + π/4 = 1.785. Since this is higher than the
pressure for penetrating flow, we should expect penetrating flow (right-hand figure).
9-16 Consider an extrusion with in a frictionless die with a = 30° and such that point
(2,4) in Figure 9.18 is on the centerline.
(a) What is the reduction?
(b) Calculate Pext/2k.
(c) Calculate η.
(d) Find the hydrostatic stress, σ2, at the centerline.
Solution: Refer to Figs. 9-18 and 9-20.
Take a cut from A through 0,2, and 1,3 to 2,4 and make an x-direction
force balance. This cut is easy to analyse because everywhere along it the
a and b lines are at 45° to x, so σx = σ1 and the net force is Fx = ∫σxdy = 0.
Using figure 9-19 and letting x and y in that figure be x' and y',
Point x' y' y = y'cos30 + (x'-1)sin30
Figure 9.49 Two possible slip-
line fields for plane-strain
compression of an octagonal
rod. For Problem 9-15.

13. A 1.0 0.0 0.0
0,2 0.638 1.366 1.00
1,3 0.904 2.12 1.788
2,4 1.335 3.195 2.935
a) hf = 2.935, ho = hf +2sin30 = 3.935
The reduction , r = (ho -hf)/ho = 0.254 or 25.4%
b) A force balance on the die walls is
PAB = P0,0 = -σ3(0,0) and σ3(0,0) = σ2(0,0) - k
so at point 0,0, σ2 = σ3 + k = -3.935Pe + k
σ2(0,2) = σ2(0,0) +2k∆φα = -3.935Pe + k + 2kπ/6 (∆φα = +π/6)
Now rotating from 0,2 to 0,3 by ∆φα = +π/12 and then from 0,3 to 1,3 by ∆φβ = -π/12σ2(0,2)
= σ2(0,0) +2k∆φα = -3.935Pe + k + 2kπ/6
σ2(1,3) = σ2(0,2) +2k(π/12) - 2k(-π/12) = -3.935Pe + k[1+(2/3)π]Now rotating from 1,3 to 1,4
by ∆φα +π/12 and then from 1,4 to 2,4 by ∆φβ = -π/12σ2(2,4) = σ2(1,3) +2k(π/12) - 2k(-π/12)
= -3.935Pe + k([1+π)
Everywhere along the cut σx = σ1 = σ2 + k
from A to 0,2 (y from 0 to 1), σ1 = -3.935Pe + 2k(1 + π/63)at 1,3 (y = 1.788), σ1 = -3.935Pe + 2k(1 +
π/3) at 2,4 (y = 2.935), σ1 = -3.935Pe + 2k(1 + π/2)
Noting that for all these points, σx = -3.935Pe + 2k + f(y), Fx = 0 = ∫σxdy may be expressed as Fx =
0 = (-3.935Pe + 2k)(2.935) +∫f(y)dy. Now plotting f(y) vs. y:
It can be seen that ∫f(y)dy = 1.πk/3 + (1.5πk/3)(1.788 -1.00) + (2.5πk/3)(2.935 -1.788) = 5.29k
Fx = 0 = -3.935Pe(2.935) + 2k(2.935) + 5.29kPe/(2k) = 0.483
c) η = wi/wa where wi = 2kεh = 2k(ln[1/(1-r)] = 0.293 and wa = Pe
η = 0.293/0.483 = 60.7%
d) at point 2,4, σ2 = -3.935Pe + (1+π)k = -3.935(.483.2k) + (1+π)k

14. σ2/(2k) = +0.170 Note that this is tensile!
9-17 Consider the slip-line field for an extrusion with a constant shear stress along the
die wall as shown in Figure 9.50.
(a) Label the α- and β-lines.
(b) Draw the Mohr’s circle diagram for the state of stress in triangle ACD showing P⊥,
τf = mk, α and β
(c) Calculate the value of m.
Solution:
c) m = τ/k = sin 30° = 0.500
9-18 At the end of an extrusion in a 90° die, a non-steady state condition develops. The
field in Figure 9.51(a) is no longer appropriate. Figure 9.51(b) is an upper-bound field for
t < 1. Calculate and plot Pext/2k as a function of t for 0.25 ≤ t ≤ 5 for the upper-bound
field. Include on your plot the value of Pext/2k for the slip-line field.
Figure 9.50 Slip-line field
for extrusion with a
constant shear stress die
interface. For Problem 9-
17.

15. Solution:
For the slip-line field (a): Along CD σ1 = 0, σ2 = k, and CBA is an α-line
σ2A = σ2ACD = σ2C + 2k∆φAC where ∆φAC = -π/2, σ2ACD = -k + 2k(-π/2) = -k(1 +
π)σ3AD = σ2ACD - k = -2k(1 + π/2) = - P⊥. P⊥ = 2k(1 + π/2); Making a force balance, P⊥
.1 =
2Pe so Pe = k(1 + π/2). Pe/(2k) = (1 + π/2)/2 = 1.285
For the upper-bound field, r = 50%, Ve = 2Vo and γ = θ
2PeVo = k( AOV*AO + OCV*OC) = k(2(t/cosθ)(Vo/cosθ),
Substituting cosθ= t/ AOand AO2 = t2 +1
2PeVo = 2kVo[t(t2+1)/t2] = 2kVo(t + 1/t), Pe/(2k) = (t + 1/t)/2
t Pe/(2k) t Pe/(2k) t Pe/( AO2k)
.25 2.125 .75 1.04 2 1.25
.375 1.52 1.0 1.0 3 1.67
.5 1.25 1.25 1.025 4 2.125
.625 1.11 1.5 1.08 5 2.6
Figure 9.51 (a) Slip-line field for a 2:1
extrusion. (b) Upper-bound field for
the end of a 2:1 extrusion. For Problem
9-18.

16. Note the general similarity with Fig. 9-30. Because of the assumption of frictionless
conditions, the result is similar to an indirect extrusion. Also prob. 9-19 addresses the
question of pipe formation
9-19 In Problem 9-18, either the slip-line field or the upper bound gives a lower
solution. However as discussed in Section 9-12, a pipe may form at the end of an
extrusion. Figure 9.52 gives an upper -bound field that leads to pipe formation.
Calculate Pext/2k as a function of t for 0.25 ≤ t ≤ 5 and compare with the solution to
Problem 9-18.
Solution:The following analysis is based on simplifying assumptions that are not correct. Yet the
results do indicate the basic reason for pipe formation in extrusion. These assumptions are:
1. 2Pe is the force applied to the piston. (It should be 2Pe(1-2x) but
this leads to messy math.
2. What is called Pe is the average value of the extrusion pressure,
which is not uniform.
Figure 9.52 An upper-bound field
for pipe formation. (Problem 9-18).

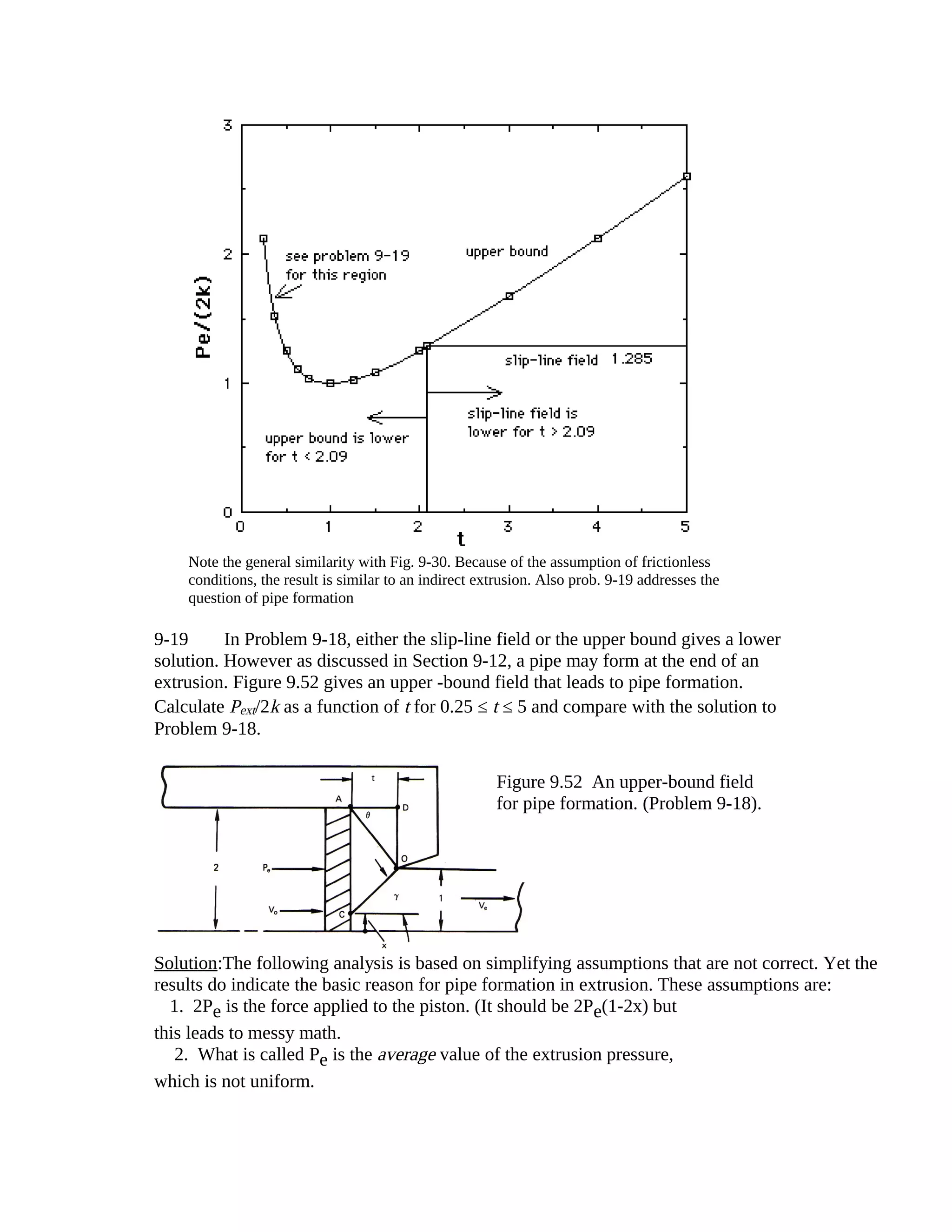
17. As point C moves upward along the piston face, x increases, and the metal adjacent to the piston
face moves faster than Vo so a pipe forms. A general hodograph is shown:
Now Ve depends on x, Ve(1-x) = Vo(2-x) or Ve = (2-x)/(1-x)Now to find the value of x for a
minimum Pe.
2VoPe = k[ AOV*AO + OCV*CO]; V*AO = Vo/cosθ and V*CO = (Ve -Vo)/cosγ,
AO= t/cosθ, OC= t/cosγ Now, V*CO = [(2-x)/(1-x) -1]/cosγ = 1/[(1-x) cosγ]
2VoPe = k{(t2+1)/t + [t2 + (1-x)2]/[t(1-x)]} (a)
Setting dPe/dx = 0 to find the minimum, t/(1-x2) -1/t = 0 or t = 1-x, so when γ = 45°, Pe is a
minimum. Substituting t = 1-x into (a),
Pe/(2k) = (1/4)[1-x + 1/(1-x) + 1 +1] = (1/4)[3 - x + 1/(1-x)]. Pe/(2k) = (1/4)[2+t+1/t]
(note this solution is valid only for t ≤ 1 (γ ≤ 45 an x ≥ 0. For t ≤ 1 the solution of Prob.
9-18 gives a lower value than the slip-line field solution)
t Pe/(2k) t Pe/(2k)
.25 1.56 .625 1.056
.375 1.26 .75 1.02
.50 1.13 1.00 1.00