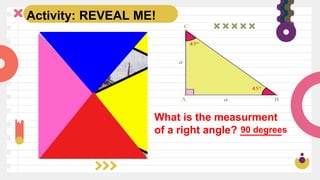
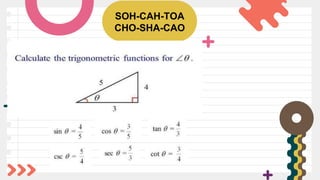
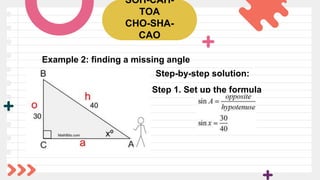
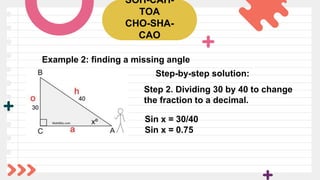
The document includes activities related to finding the missing lengths of sides in right triangles, as well as trivia about the rigidity of triangles and their applications in construction. It emphasizes learning objectives focused on the six trigonometric functions and their real-life applications. Additionally, there are examples demonstrating how to find missing angles using sine functions and a couple of assignments for practical engagement.

1. Activity
Find the missing length of the
following right triangles and
answer the items that follow.

2. Questions:
1. For ∆ABC, the value of the side a is equal to
? ______
2. For ∆DEF, the length of the side b is equal
to? _____
3. For ∆GHI, the length of side c is? ____
15.5
5.2
9.2

3. Trivia Time!
Did you know that triangle is the strongest
shape? If you try to create a shape out of
sticks joined with hinges for example
square even without force applied it will be
transformed into a parallelogram but
triangles will not, for a triangle no matter
what type, this can’t happen. It’s
inherently rigid.

4. Trivia Time!
That’s why this shape is very common on buildings
and other construction. That’s why some build
landmarks like this.

5. Activity: REVEAL ME!
What is the measurment
of a right angle? _______
90 degrees

6. Activity: REVEAL ME!
What is the value of the
hypotenuse? _______
12
12
10
8

7. Activity:REVEAL ME!
What is the name of the
side adjacent to angle C?
_______
b
a
b
c
A
B
C

8. Activity:REVEAL ME!
What is the non-
hypotenuse side that is
next to angle M? _______
a
a
b
c
A
M
T

9. Activity:REVEAL ME!
Hipparchus was a Greek
astronomer, geographer,
and mathematician. He is
considered the founder
of trigonometry.
HIPPARCHUS OF NICAEA

10. By: NELBERT D. SORIANO
ILLUSTRATING THE
SIX TRIGONOMETRIC
RATIOS

11. At the end of the lesson, the student should be able
to:
 Illustrate the six trigonometric functions: sine,
cosine, tangent, cosecant, secant, and
cotangent;
 Apply the six trigonometric functions to solve
right triangles; and
 Appreciate the trigonometric function by solving
real-life problems.
LEARNING OBJECTIVES:

12. -Trigonometric ratios are ratios of the length of
sides of a triangle. These ratios in trigonometry
relate the ratio of sides of a right triangle to the
respective angle.
The six trigonometric ratios
-The six trigonometric ratios namely Sine,
Cosine, Tangent, Cosecant, Secant, and
Cotangent are abbreviated below

13. The six trigonometric ratios

14. SOH-CAH-TOA
CHO-SHA-CAO

15. SOH-CAH-
TOA
CHO-SHA-
CAO
Example 2: finding a missing angle
Step-by-step solution:
Step 1. Set up the formula

16. SOH-CAH-
TOA
CHO-SHA-
CAO
Example 2: finding a missing angle
Step-by-step solution:
Step 2. Dividing 30 by 40 to change
the fraction to a decimal.
Sin x = 30/40
Sin x = 0.75

17. SOH-CAH-
TOA
CHO-SHA-
CAO
Example 2: finding a missing angle
Step-by-step solution:
Step 3. Find an angle whose sine is
0.75 by using the sin-¹ function on
your calculator.
Sin x = 0.75
sin-¹ (sin x) = sin-¹ (0.75)
x = sin-¹ (0.75)
x = 48.59037789 or 49°

18. How can we apply or relate he
use of these trigonometric
function in a real-world?

19. Real-world application

20. Assignment: Challenge problemsl

21. QUIZ
1. Find the day of the week you were born, and of your
birthday this year.
2. Set up a round-robin tournament schedule for 9
teams.

22. Type equation here.