Embed presentation
Downloaded 20 times


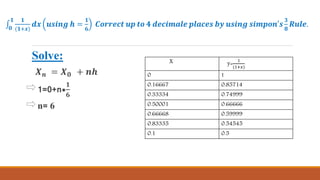
![Simpsons 3/8 rule:
I=
𝟑𝒉
𝟖
[𝒚 𝟎+𝟑𝒚 𝟏+3𝒚 𝟐+2𝒚 𝟑 + 𝟑𝒚 𝟒 + 𝟑𝒚 𝟓+𝒚 𝟔]
=0.69320
Exact ∶ 𝟎
𝟏 𝟏
(𝟏+𝒙)
𝒅𝒙
= [𝑙𝑛(1+x) ] 𝟎
𝟏
= 𝑙𝑛2- 𝑙𝑛1
=.69315](https://image.slidesharecdn.com/math-160406041006/85/simpson-s-in-numerical-method-5-320.jpg)

![Simpsons 3/8 rule:
I=3h/8[𝑦0+3𝑦1+3𝑦2+2𝑦3 + 3𝑦4 + 3𝑦5+𝑦6]
=1.82784](https://image.slidesharecdn.com/math-160406041006/85/simpson-s-in-numerical-method-7-320.jpg)


This document demonstrates using Simpson's 3/8 rule to approximate two integrals. For the integral from 0 to 1 of (1+x), Simpson's 3/8 rule gives a result of 0.69320, which approximates the exact solution of 0.69315. For the integral from 4 to 5.2 of ln(x), Simpson's 3/8 rule gives a result of 1.82784.




![Simpsons 3/8 rule:
I=
𝟑𝒉
𝟖
[𝒚 𝟎+𝟑𝒚 𝟏+3𝒚 𝟐+2𝒚 𝟑 + 𝟑𝒚 𝟒 + 𝟑𝒚 𝟓+𝒚 𝟔]
=0.69320
Exact ∶ 𝟎
𝟏 𝟏
(𝟏+𝒙)
𝒅𝒙
= [𝑙𝑛(1+x) ] 𝟎
𝟏
= 𝑙𝑛2- 𝑙𝑛1
=.69315](https://image.slidesharecdn.com/math-160406041006/85/simpson-s-in-numerical-method-5-320.jpg)

![Simpsons 3/8 rule:
I=3h/8[𝑦0+3𝑦1+3𝑦2+2𝑦3 + 3𝑦4 + 3𝑦5+𝑦6]
=1.82784](https://image.slidesharecdn.com/math-160406041006/85/simpson-s-in-numerical-method-7-320.jpg)
