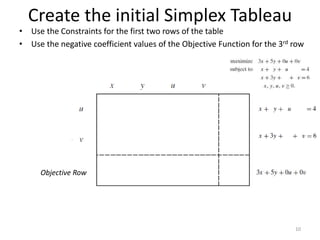
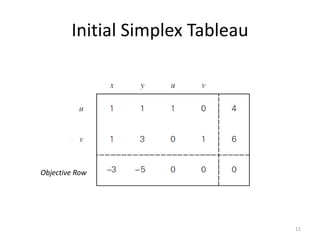
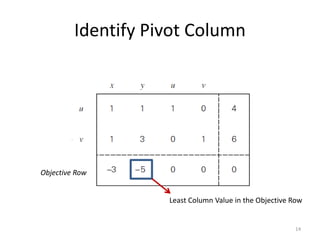
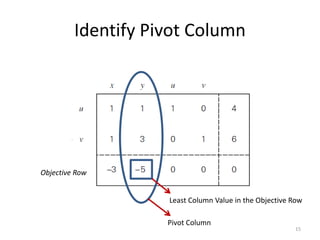
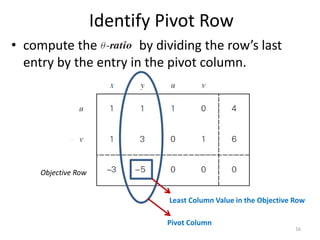
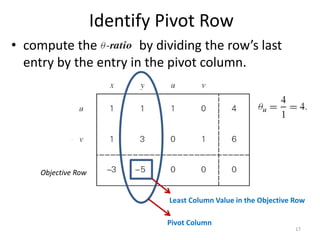
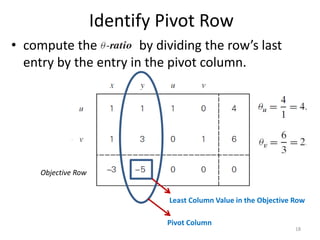
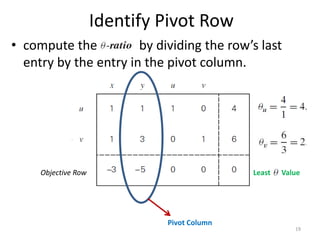
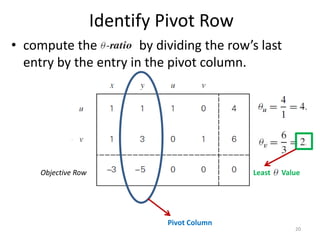
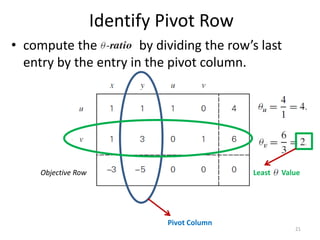
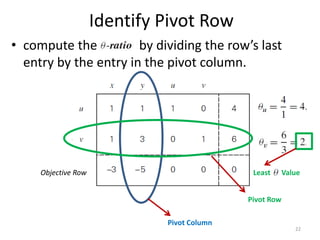
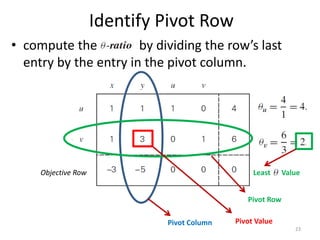
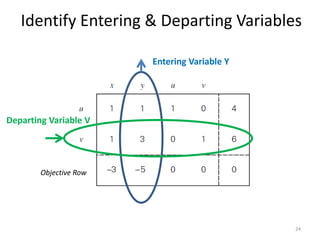
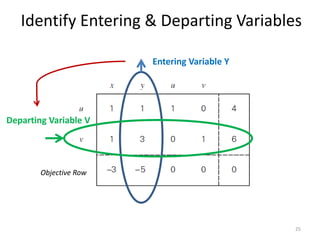
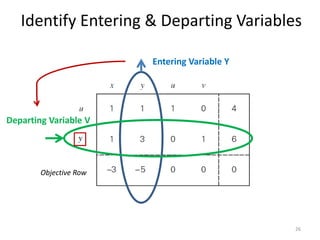
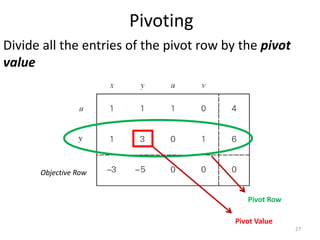
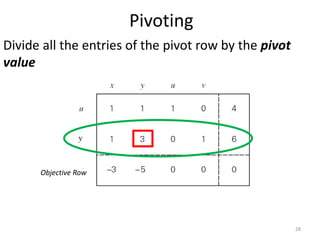
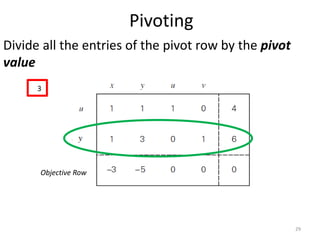
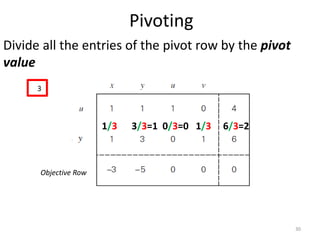
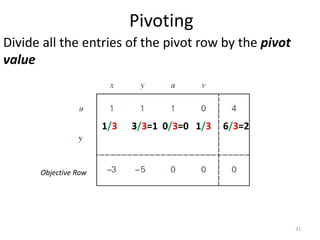
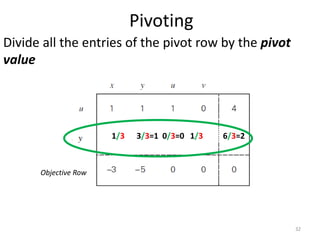
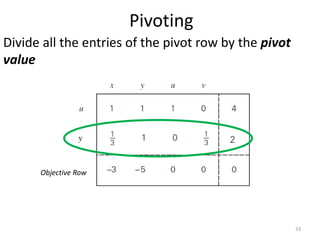
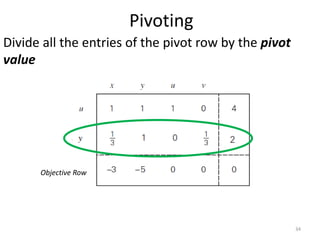
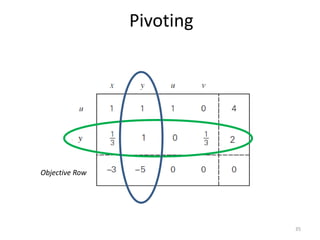
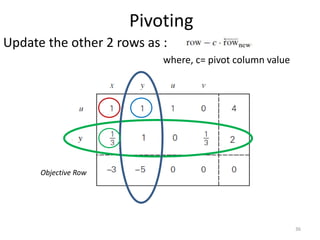
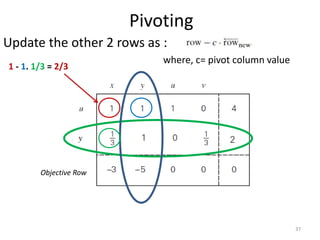
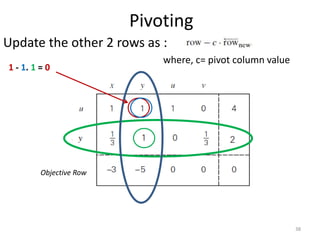
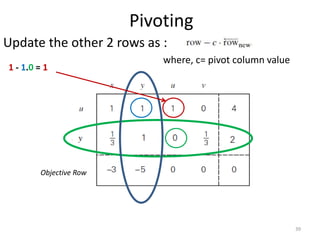
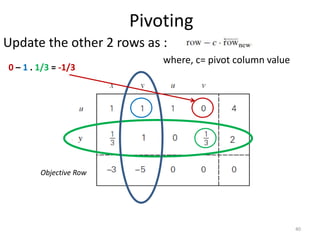
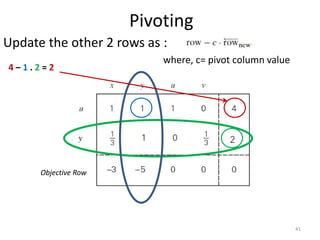
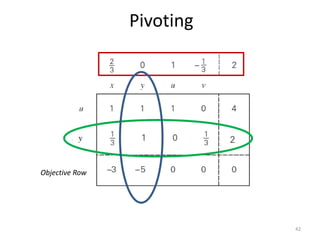
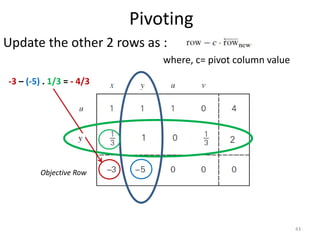
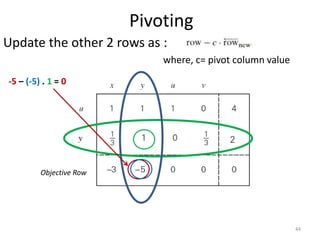
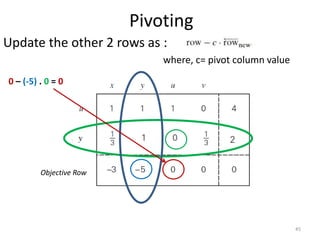
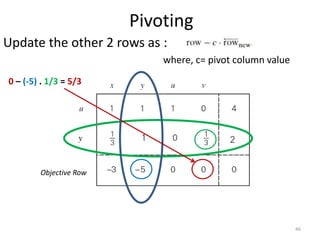
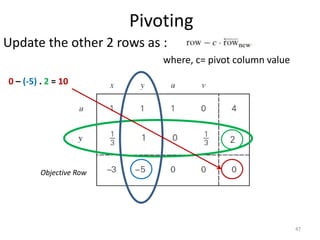
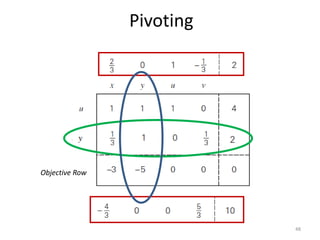
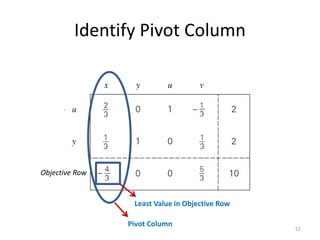
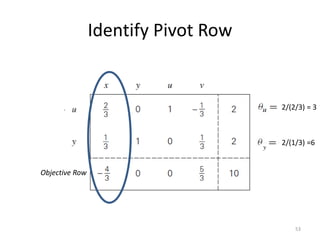
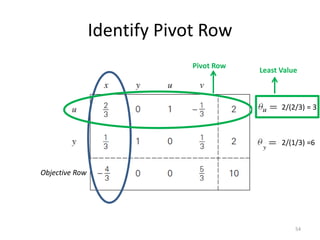
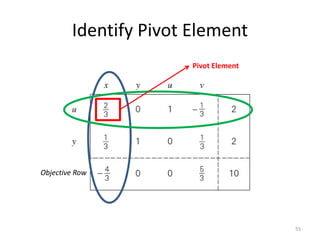
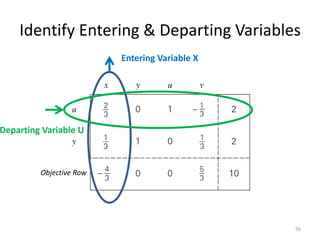
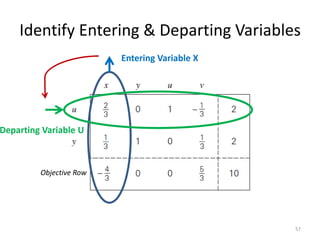
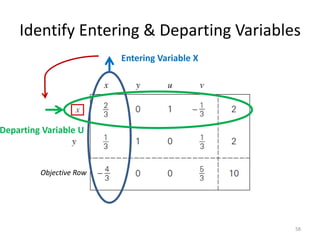
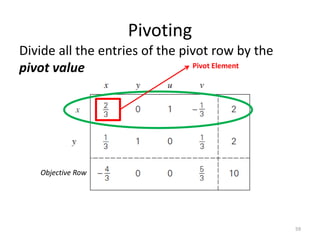
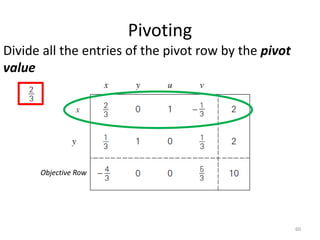
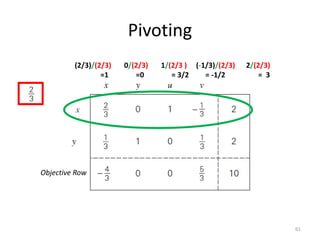
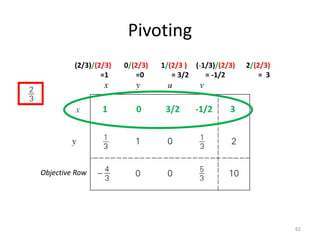
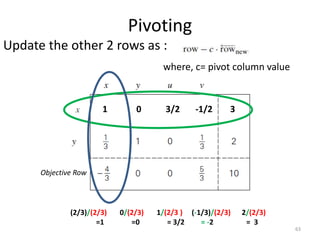
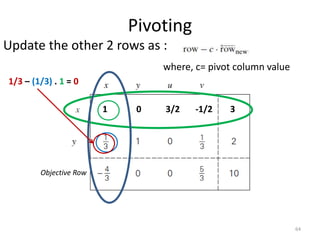
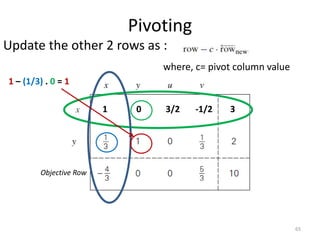
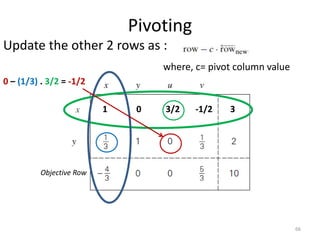
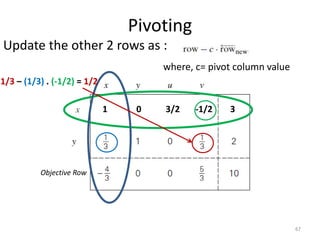
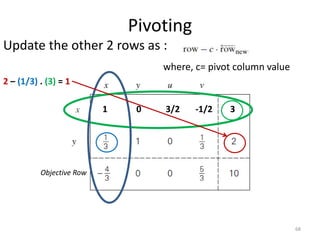
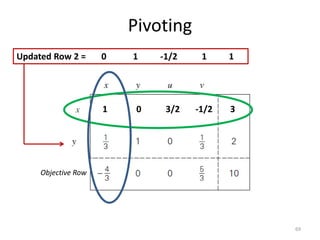
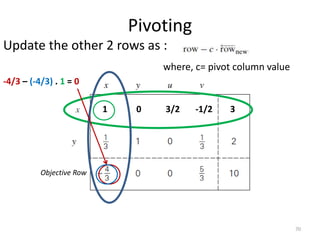
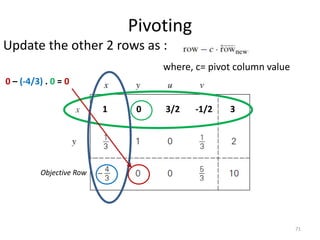
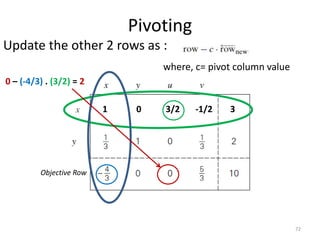
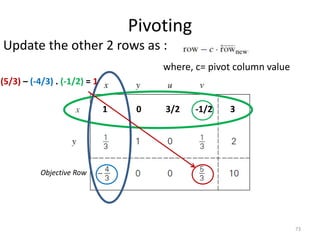
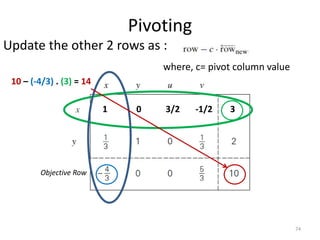
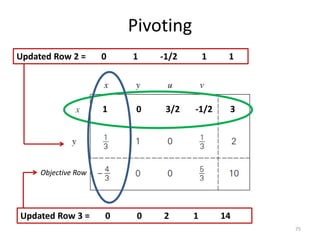
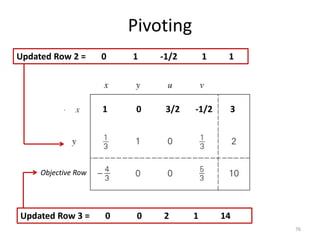
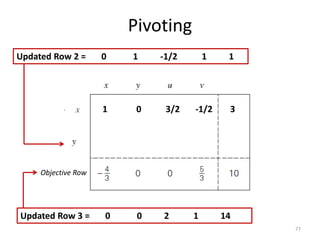
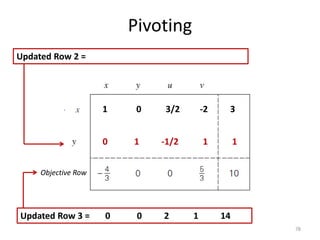
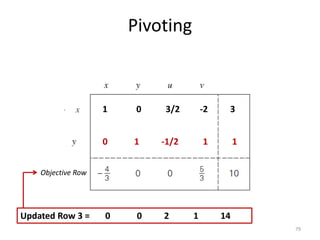
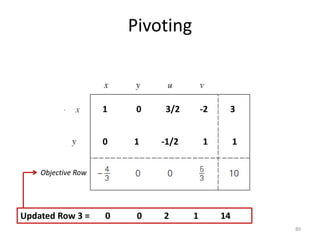
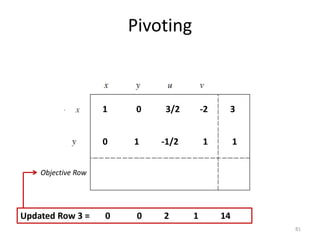
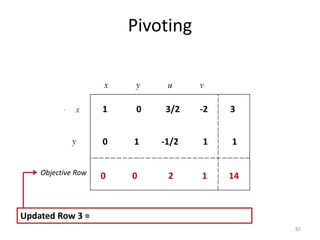
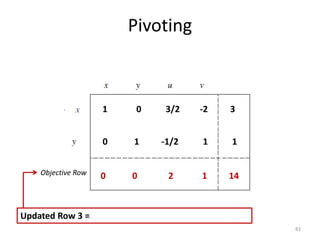
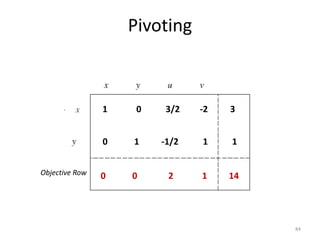
The document describes the simplex method for solving linear programming problems. It provides an example problem in standard form and walks through two iterations of the simplex method to find the optimal solution. The key steps of the simplex method include identifying the entering and departing variables, calculating the pivot element, pivoting the rows, and checking for convergence. After two iterations, the example problem converges to an optimal objective value of 14 when x=3 and y=1.

1. SIMPLEX METHOD
ITERATIVE IMPROVEMENT METHOD
1
Dr. P. Subathra
Professor/ IT
KAMARAJ College of Engg. & Tech.
(AUTONOMOUS)

2. SIMPLEX METHOD
The general problem of optimizing a linear
function of several variables subject to a set of
linear constraints:
2

3. SIMPLEX METHOD
• Consider the following linear programming problem in two
variables:
• A feasible solution to this problem is any point (x, y) that
satisfies all the constraints of the problem
• An optimal solution, a point in the feasible region with the
largest value of the objective function z = 3x + 5y.
• Our task is to find an optimal solution
3

4. SIMPLEX METHOD
• To apply the simplex method to a linear
programming problem, it has to be represented
in a special form called the standard form.
• The standard form has the following
requirements:
– It must be a maximization problem.
– All the constraints (except the nonnegativity
constraints) must be in the form of linear equations
with nonnegative right-hand sides.
– All the variables must be required to be nonnegative.
4

5. SIMPLEX METHOD
5

6. SIMPLEX METHOD – Solved Example
6

7. SIMPLEX METHOD – Solved Example
• Constraint is given as an inequality
• Add slack variable to convert it into equivalent
equation.
7

8. SIMPLEX METHOD – Solved Example
• Convert the given problem into a the standard
form of linear programming problem in four
variables:
8

9. SIMPLEX METHOD – Solved Example
• Now the Problem is of the standard form:
9

10. Create the initial Simplex Tableau
• Use the Constraints for the first two rows of the table
• Use the negative coefficient values of the Objective Function for the 3rd row
Objective Row
10

11. Initial Simplex Tableau
Objective Row
11

12. ITERATION 1
12

13. Steps to be Followed
• Find Entering Variable
– Find the Pivot Column
• Find Departing Variable
– Calculate value
– Find the Pivot Row
• Find Pivot Value (c)
• Pivoting
– Update the Pivot Row with the Pivot Value (row/c)
– Update the other Two Rows
• Check for Convergence
13

14. Identify Pivot Column
Least Column Value in the Objective Row
Objective Row
14

15. Identify Pivot Column
Least Column Value in the Objective Row
Objective Row
Pivot Column
15

16. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Least Column Value in the Objective Row
Objective Row
Pivot Column
16

17. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Least Column Value in the Objective Row
Objective Row
Pivot Column
17

18. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Least Column Value in the Objective Row
Objective Row
Pivot Column
18

19. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Objective Row
Pivot Column
Least Value
19

20. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Objective Row
Pivot Column
Least Value
20

21. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Objective Row
Pivot Column
Least Value
21

22. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Objective Row
Pivot Column
Least Value
Pivot Row
22

23. Identify Pivot Row
• compute the by dividing the row’s last
entry by the entry in the pivot column.
Objective Row
Pivot Column
Least Value
Pivot Row
Pivot Value
23

24. Identify Entering & Departing Variables
Objective Row
24
Entering Variable Y
Departing Variable V

25. Identify Entering & Departing Variables
Objective Row
25
Entering Variable Y
Departing Variable V

26. Identify Entering & Departing Variables
Objective Row
26
Entering Variable Y
Departing Variable V

27. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
Pivot Row
Pivot Value
27

28. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
28

29. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
3
29

30. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
1/3 3/3=1 0/3=0 1/3 6/3=2
3
30

31. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
1/3 3/3=1 0/3=0 1/3 6/3=2
31

32. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
32
1/3 3/3=1 0/3=0 1/3 6/3=2

33. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
33

34. Pivoting
Divide all the entries of the pivot row by the pivot
value
Objective Row
34

35. Pivoting
Objective Row
35

36. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
36

37. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
37
1 - 1. 1/3 = 2/3

38. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
38
1 - 1. 1 = 0

39. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
39
1 - 1.0 = 1

40. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
40
0 – 1 . 1/3 = -1/3

41. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
41
4 – 1 . 2 = 2

42. Pivoting
Objective Row
42

43. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
43
-3 – (-5) . 1/3 = - 4/3

44. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
44
-5 – (-5) . 1 = 0

45. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
45
0 – (-5) . 0 = 0

46. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
46
0 – (-5) . 1/3 = 5/3

47. Pivoting
Update the other 2 rows as :
where, c= pivot column value
Objective Row
47
0 – (-5) . 2 = 10

48. Pivoting
Objective Row
48

49. Simplex Tableau after First Iteration
Check for Convergence: If all values in objective
row are positive, then converged. NO!
49
Objective Row

50. ITERATION 2
50

51. Steps to be Followed
• Find Entering Variable
– Find the Pivot Column
• Find Departing Variable
– Calculate value
– Find the Pivot Row
• Find Pivot Value (c)
• Pivoting
– Update the Pivot Row with the Pivot Value (row/c)
– Update the other Two Rows
• Check for Convergence
51

52. Identify Pivot Column
52
Least Value in Objective Row
Pivot Column
Objective Row

53. Identify Pivot Row
53
2/(2/3) = 3
2/(1/3) =6
Objective Row

54. Identify Pivot Row
54
2/(2/3) = 3
2/(1/3) =6
Objective Row
Least Value
Pivot Row

55. Identify Pivot Element
55
Objective Row
Pivot Element

56. Identify Entering & Departing Variables
56
Objective Row
Departing Variable U
Entering Variable X

57. Identify Entering & Departing Variables
57
Objective Row
Departing Variable U
Entering Variable X

58. Identify Entering & Departing Variables
58
Objective Row
Departing Variable U
Entering Variable X

59. Pivoting
Divide all the entries of the pivot row by the
pivot value
59
Objective Row
Pivot Element

60. Pivoting
Divide all the entries of the pivot row by the pivot
value
60
Objective Row

61. Pivoting
61
Objective Row
(2/3)/(2/3) 0/(2/3) 1/(2/3 ) (-1/3)/(2/3) 2/(2/3)
=1 =0 = 3/2 = -1/2 = 3

62. Pivoting
62
Objective Row
(2/3)/(2/3) 0/(2/3) 1/(2/3 ) (-1/3)/(2/3) 2/(2/3)
=1 =0 = 3/2 = -1/2 = 3
1 0 3/2 -1/2 3

63. Pivoting
Update the other 2 rows as :
where, c= pivot column value
63
Objective Row
(2/3)/(2/3) 0/(2/3) 1/(2/3 ) (-1/3)/(2/3) 2/(2/3)
=1 =0 = 3/2 = -2 = 3
1 0 3/2 -1/2 3

64. Pivoting
Update the other 2 rows as :
where, c= pivot column value
64
Objective Row
1 0 3/2 -1/2 3
1/3 – (1/3) . 1 = 0

65. Pivoting
Update the other 2 rows as :
where, c= pivot column value
65
Objective Row
1 0 3/2 -1/2 3
1 – (1/3) . 0 = 1

66. Pivoting
Update the other 2 rows as :
where, c= pivot column value
66
Objective Row
1 0 3/2 -1/2 3
0 – (1/3) . 3/2 = -1/2

67. Pivoting
Update the other 2 rows as :
where, c= pivot column value
67
Objective Row
1 0 3/2 -1/2 3
1/3 – (1/3) . (-1/2) = 1/2

68. Pivoting
Update the other 2 rows as :
where, c= pivot column value
68
Objective Row
1 0 3/2 -1/2 3
2 – (1/3) . (3) = 1

69. Pivoting
69
Objective Row
1 0 3/2 -1/2 3
Updated Row 2 = 0 1 -1/2 1 1

70. Pivoting
Update the other 2 rows as :
where, c= pivot column value
70
Objective Row
1 0 3/2 -1/2 3
-4/3 – (-4/3) . 1 = 0

71. Pivoting
Update the other 2 rows as :
where, c= pivot column value
71
Objective Row
1 0 3/2 -1/2 3
0 – (-4/3) . 0 = 0

72. Pivoting
Update the other 2 rows as :
where, c= pivot column value
72
Objective Row
1 0 3/2 -1/2 3
0 – (-4/3) . (3/2) = 2

73. Pivoting
Update the other 2 rows as :
where, c= pivot column value
73
Objective Row
1 0 3/2 -1/2 3
(5/3) – (-4/3) . (-1/2) = 1

74. Pivoting
Update the other 2 rows as :
where, c= pivot column value
74
Objective Row
1 0 3/2 -1/2 3
10 – (-4/3) . (3) = 14

75. Pivoting
75
Objective Row
1 0 3/2 -1/2 3
Updated Row 2 = 0 1 -1/2 1 1
Updated Row 3 = 0 0 2 1 14

76. Pivoting
76
Objective Row
1 0 3/2 -1/2 3
Updated Row 2 = 0 1 -1/2 1 1
Updated Row 3 = 0 0 2 1 14

77. Pivoting
77
Objective Row
1 0 3/2 -1/2 3
Updated Row 2 = 0 1 -1/2 1 1
Updated Row 3 = 0 0 2 1 14

78. Pivoting
78
Objective Row
1 0 3/2 -2 3
Updated Row 2 =
Updated Row 3 = 0 0 2 1 14
0 1 -1/2 1 1

79. Pivoting
79
Objective Row
1 0 3/2 -2 3
Updated Row 3 = 0 0 2 1 14
0 1 -1/2 1 1

80. Pivoting
80
Objective Row
1 0 3/2 -2 3
Updated Row 3 = 0 0 2 1 14
0 1 -1/2 1 1

81. Pivoting
81
Objective Row
1 0 3/2 -2 3
Updated Row 3 = 0 0 2 1 14
0 1 -1/2 1 1

82. Pivoting
82
Objective Row
1 0 3/2 -2 3
Updated Row 3 =
0 1 -1/2 1
0 0 2 1
1
14

83. Pivoting
83
Objective Row
1 0 3/2 -2 3
Updated Row 3 =
0 1 -1/2 1
0 0 2 1
1
14

84. Pivoting
84
Objective Row
1 0 3/2 -2 3
0 1 -1/2 1
0 0 2 1
1
14

85. Pivoting
Check for Convergence:
All Values in Objective row =Positive? YES!!!
85
Objective Row
1 0 3/2 -2 3
0 1 -1/2 1
0 0 2 1
1
14

86. Pivoting
Final Solution: Optimal Maximum value of
Z = 14, When X = 3 and Y = 1
86
Objective Row
1 0 3/2 -2 3
0 1 -1/2 1
0 0 2 1
1
14

87. 87

88. 88