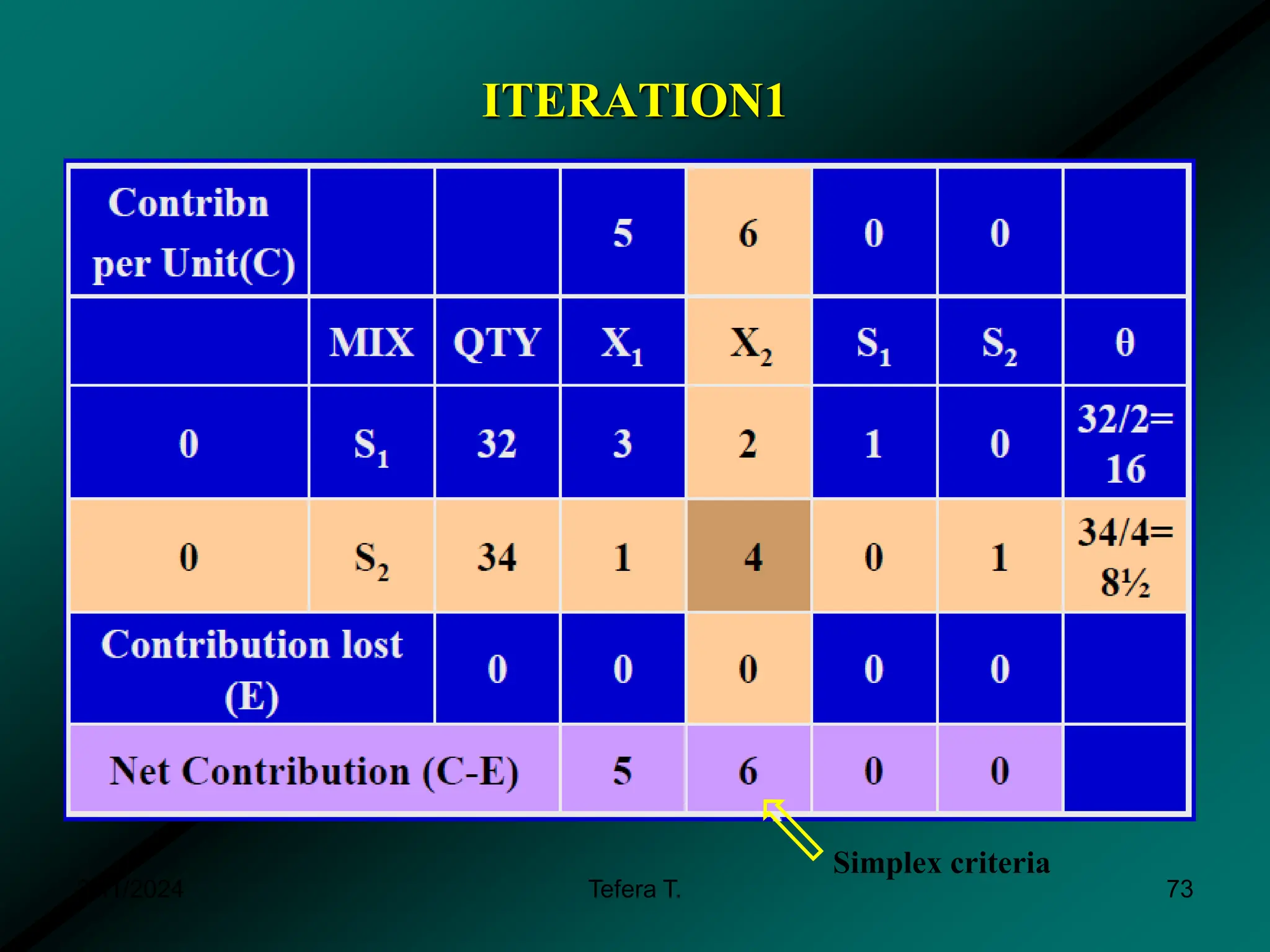
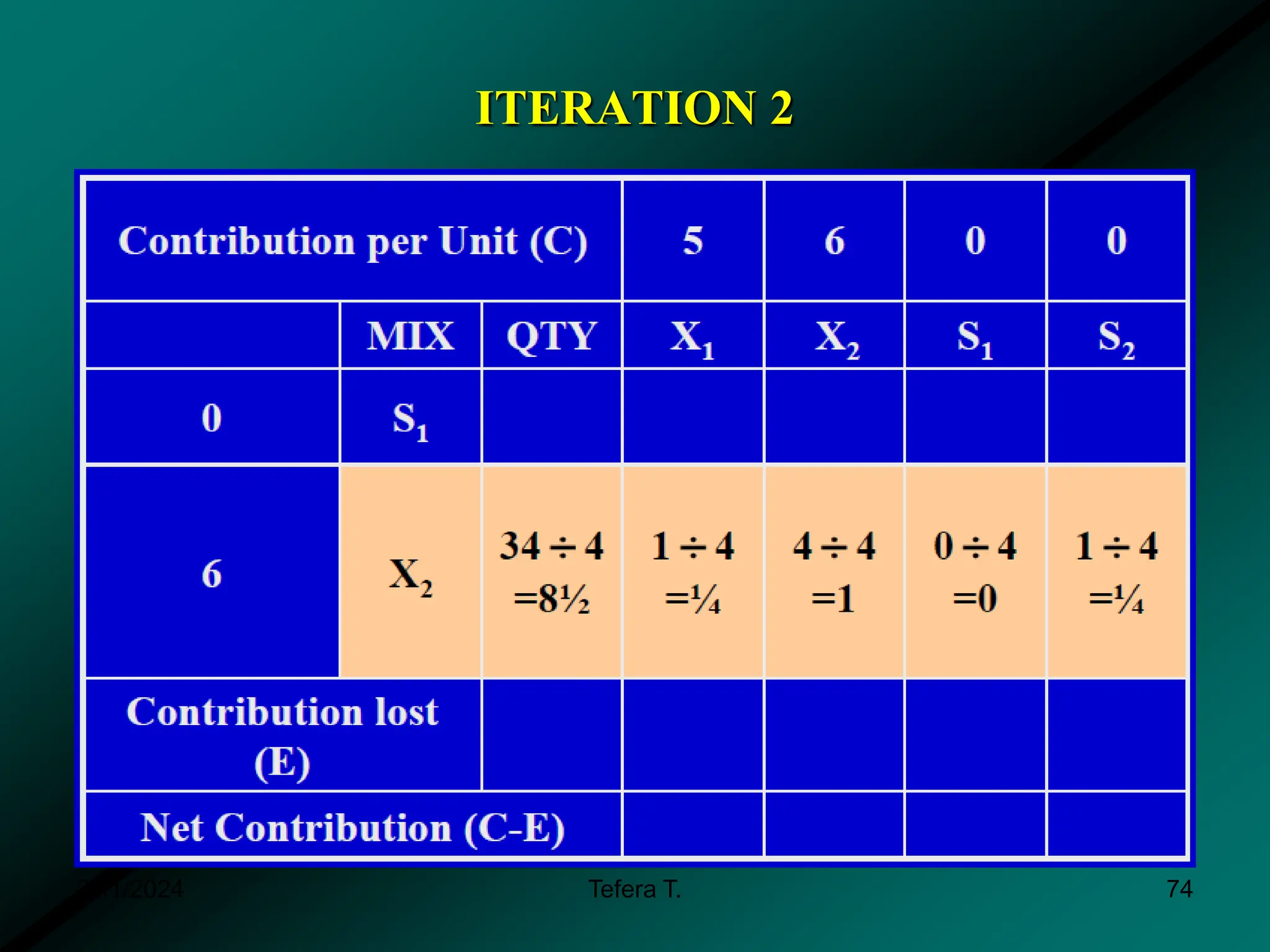
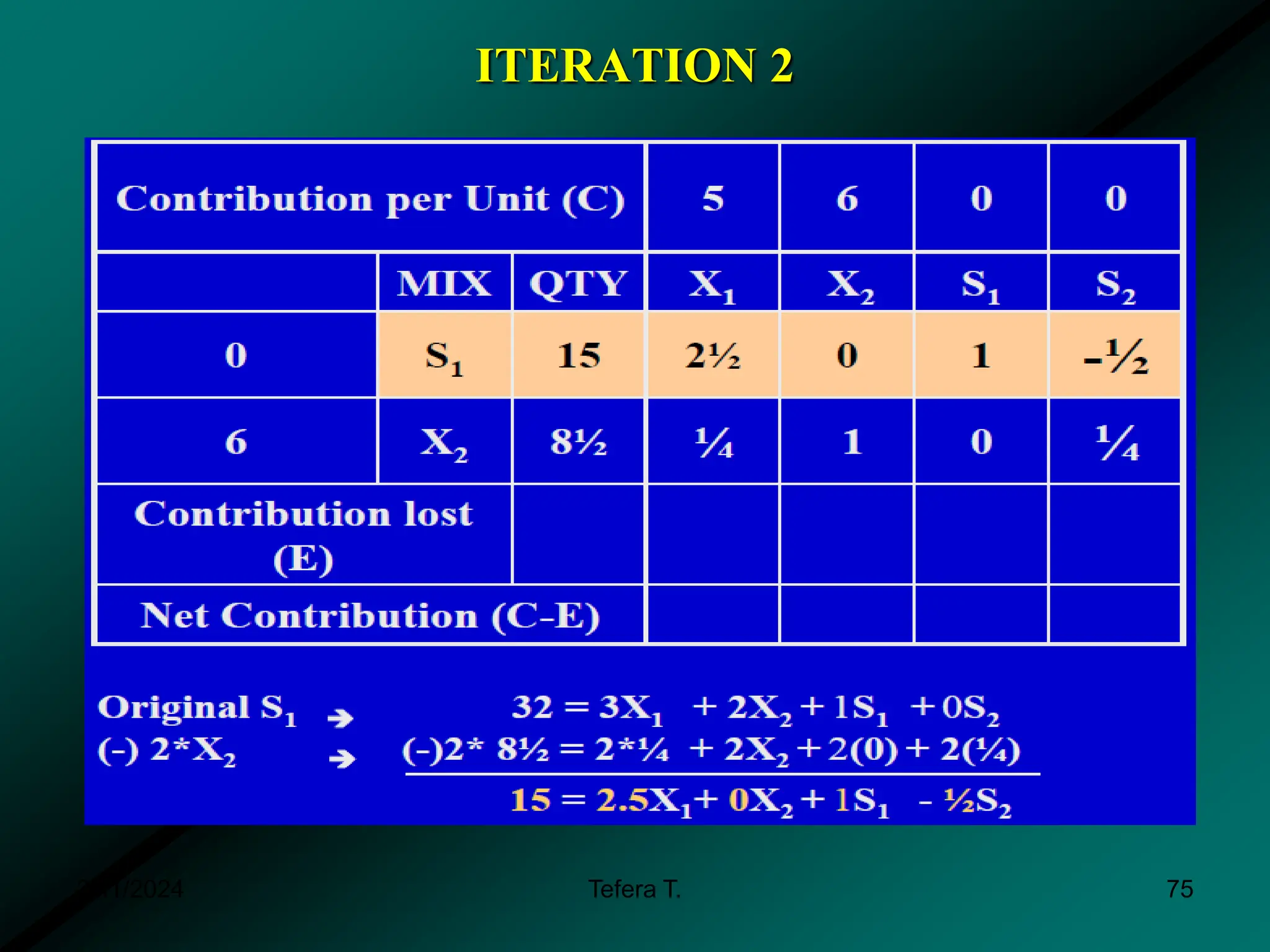
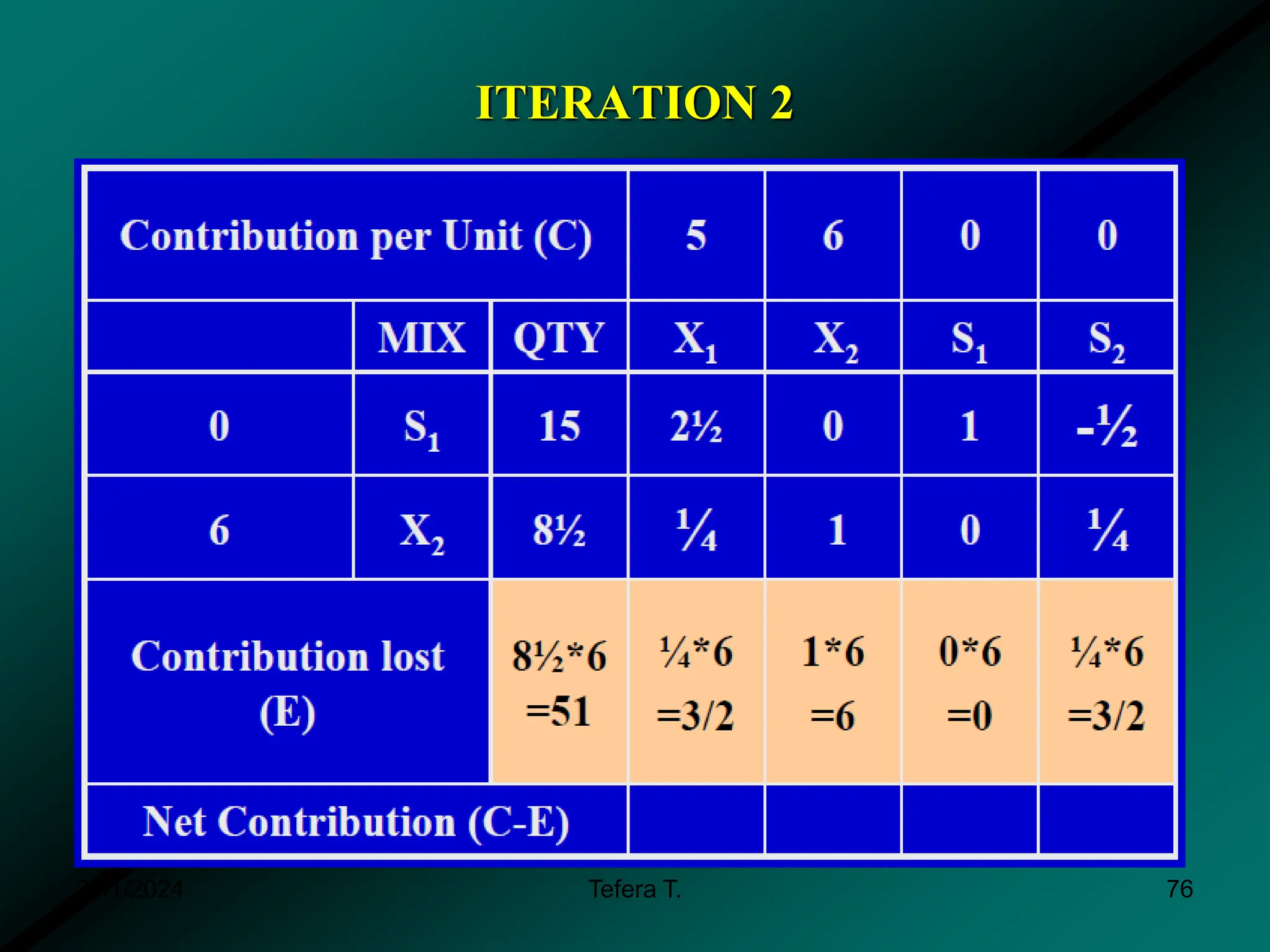
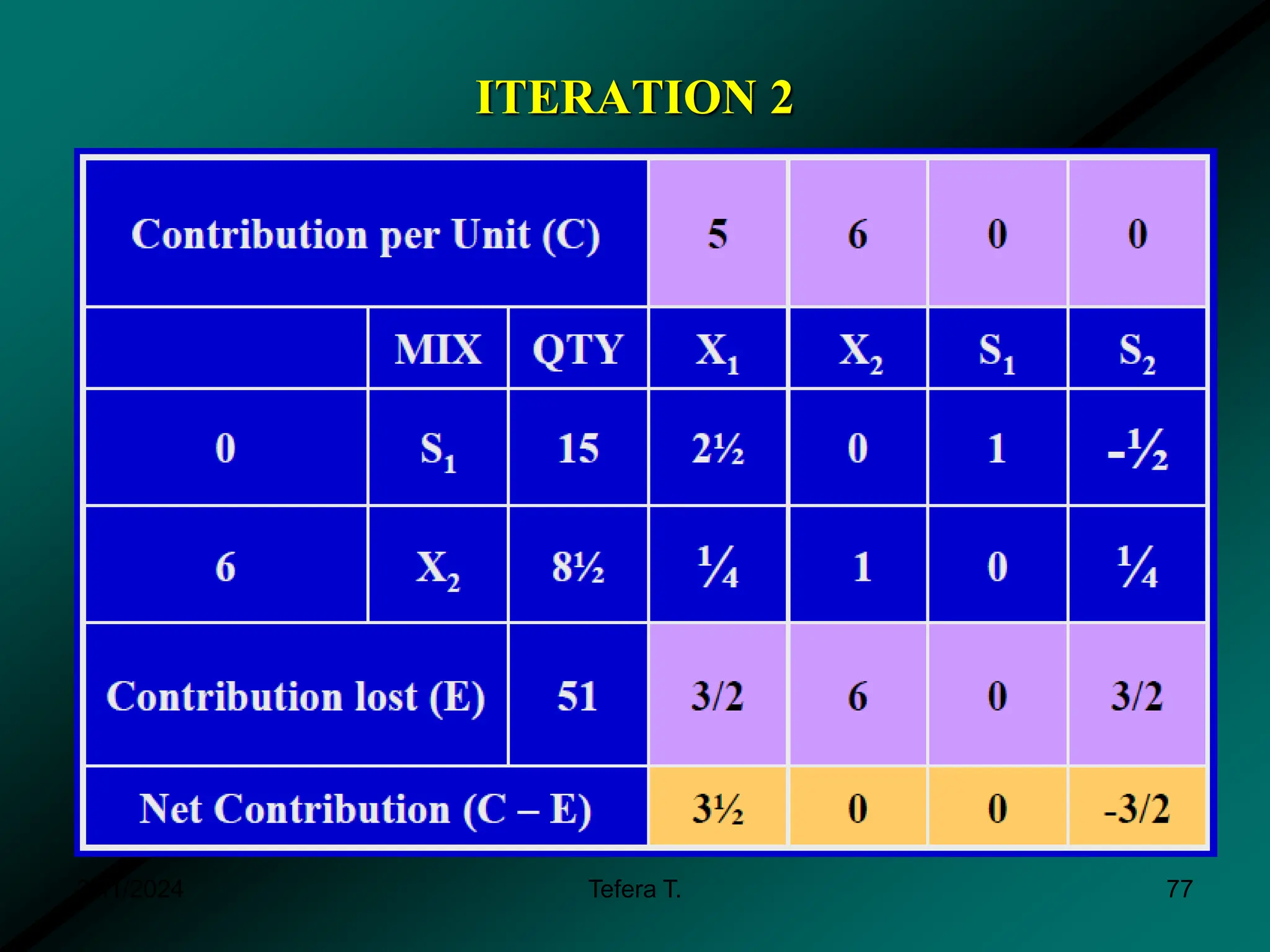
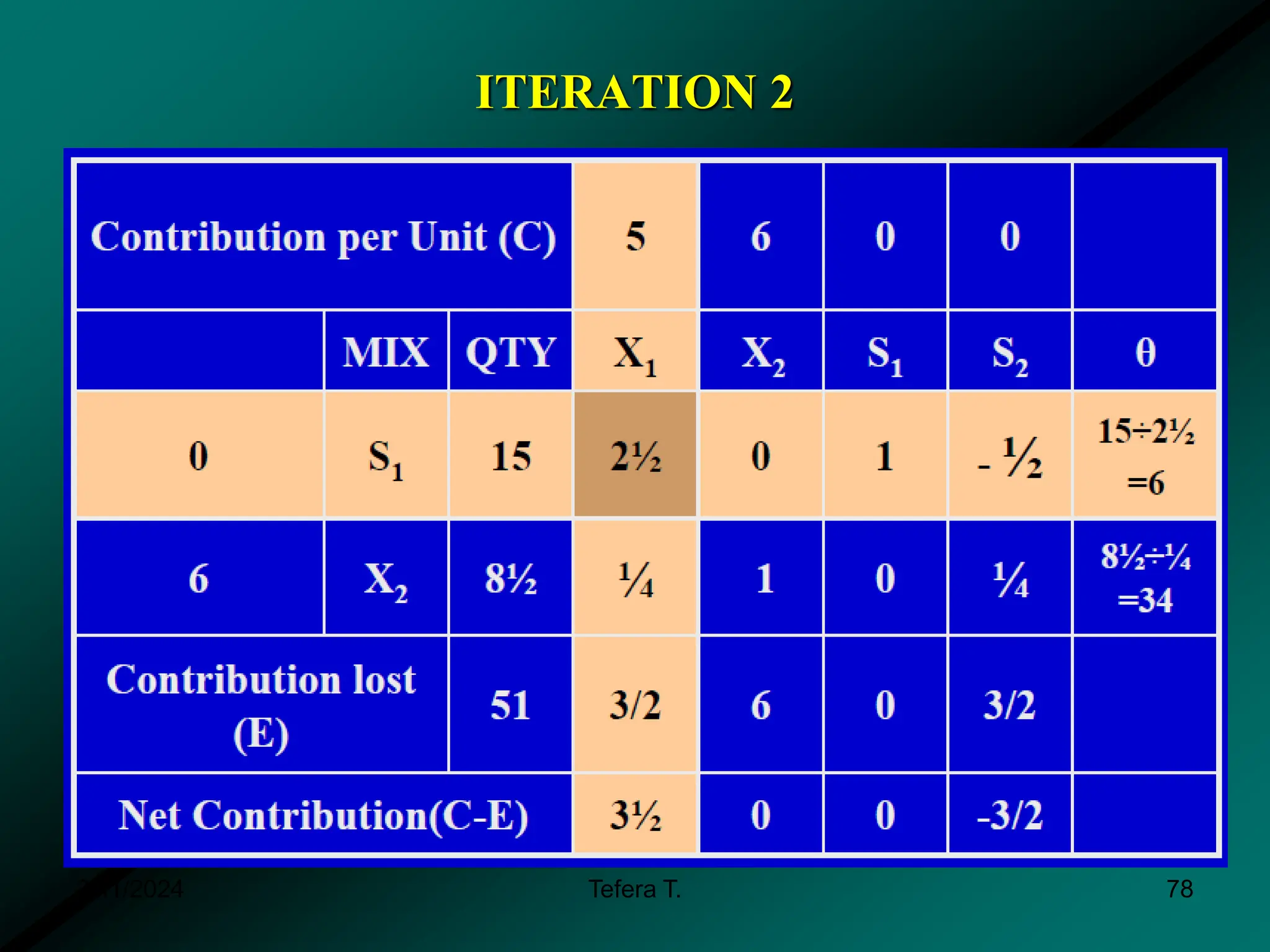
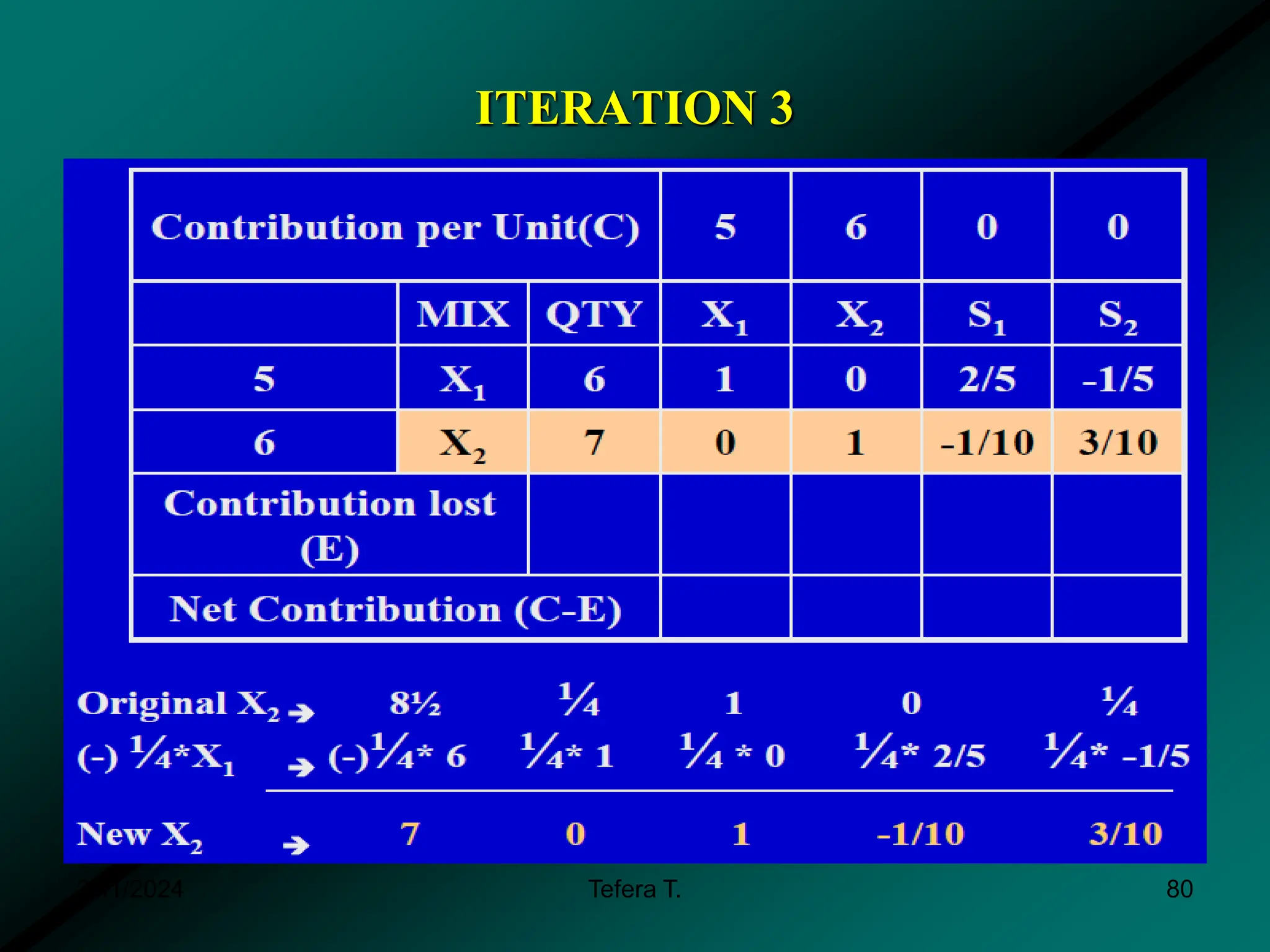
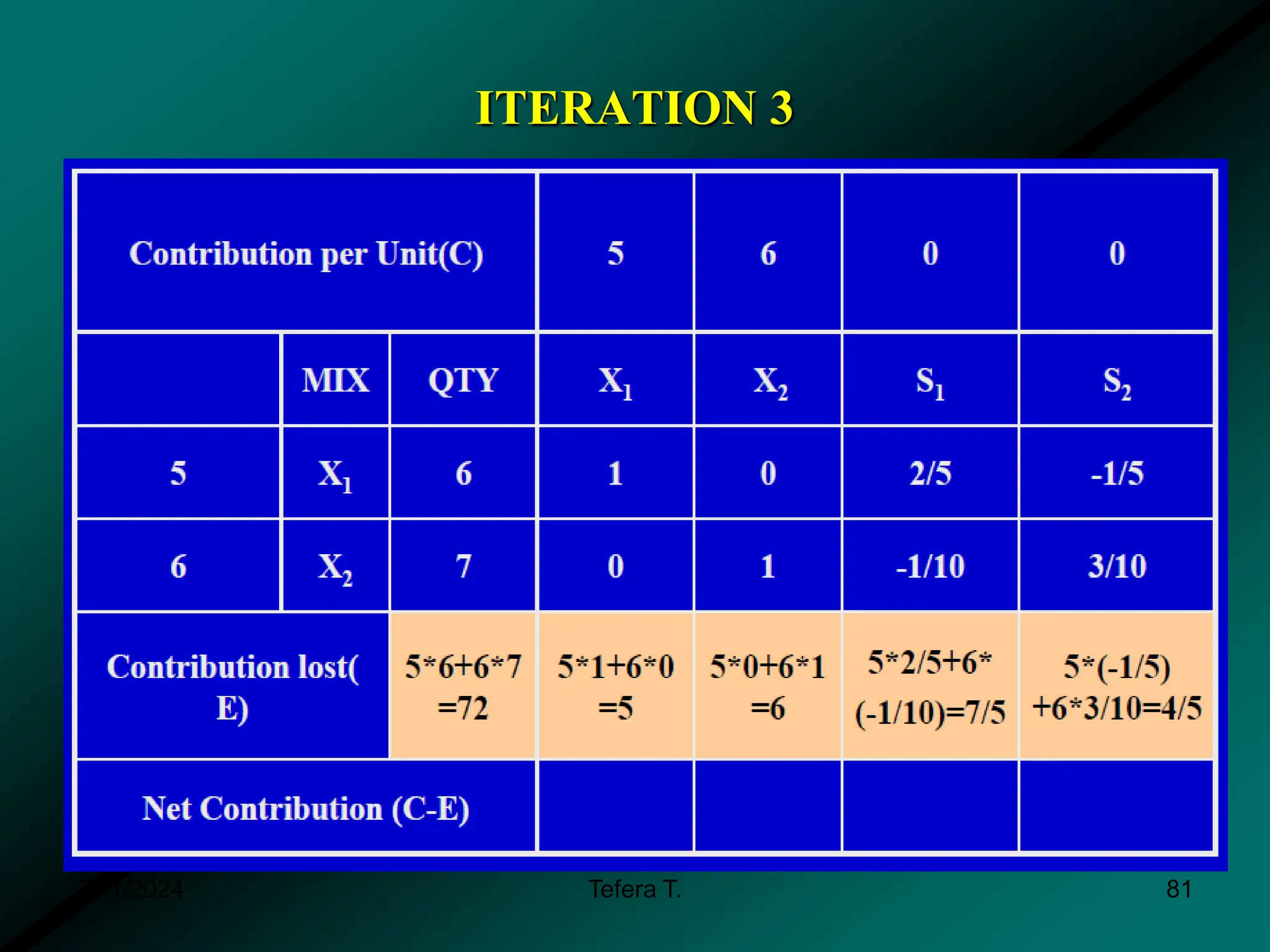
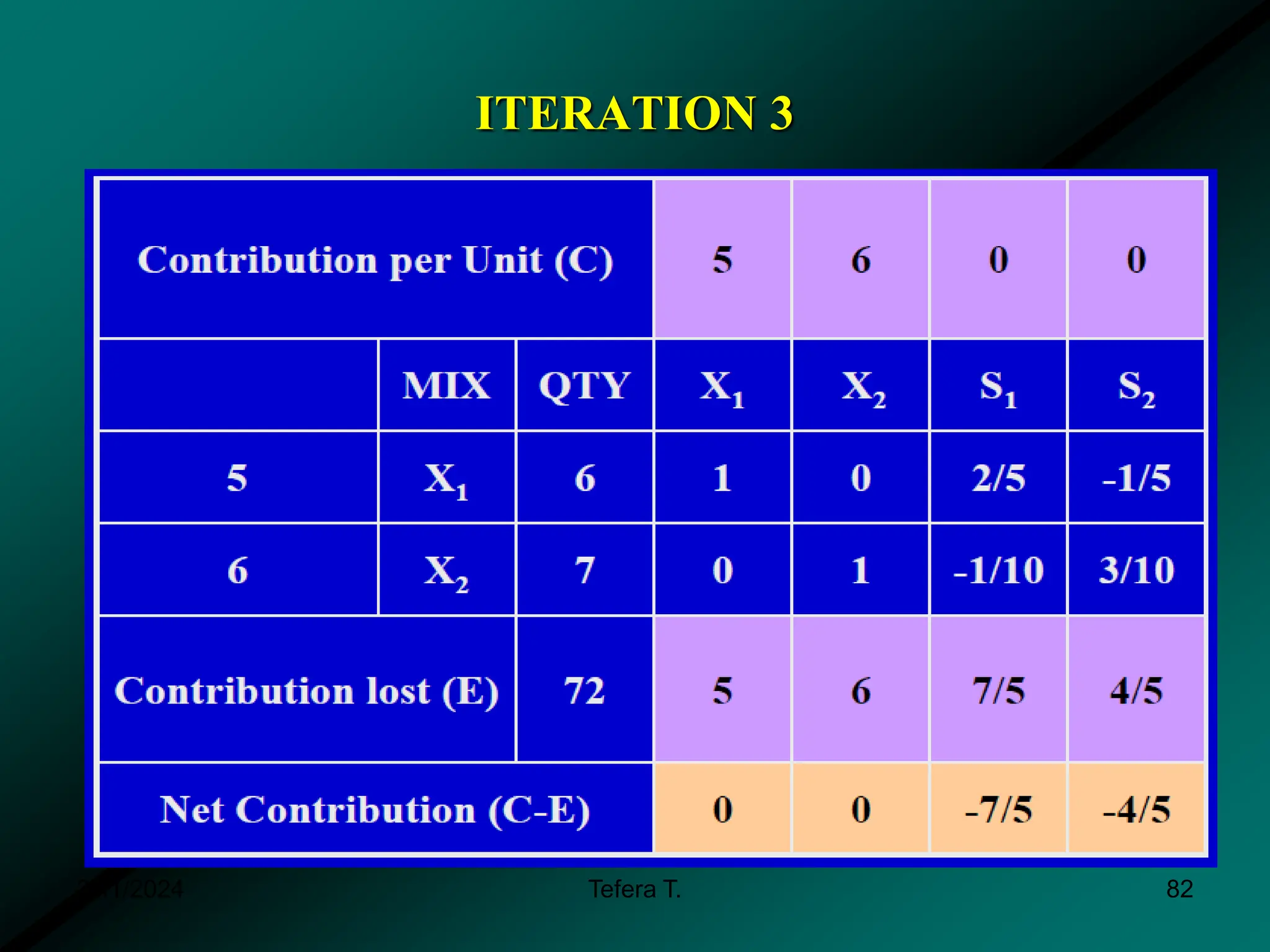
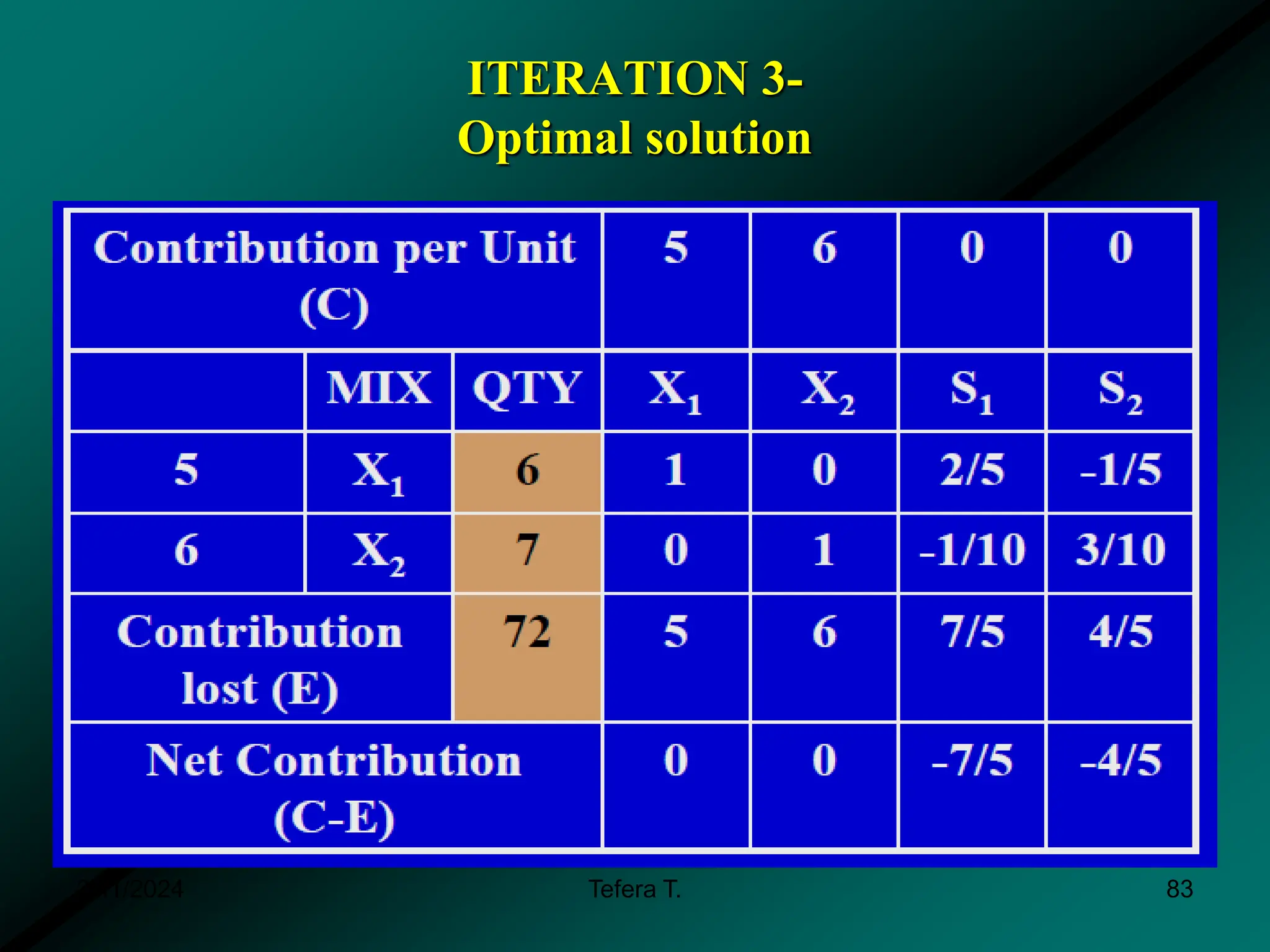
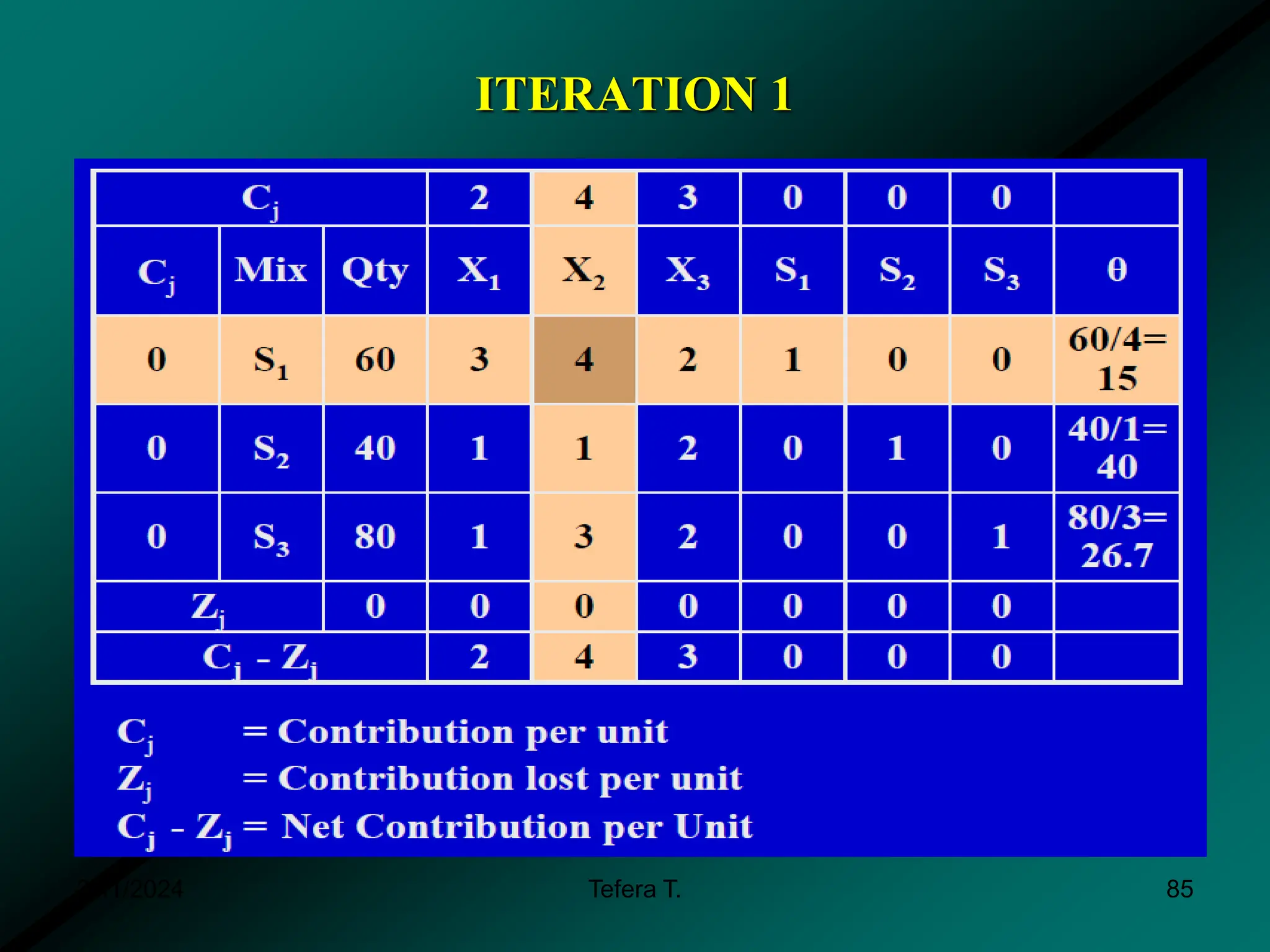
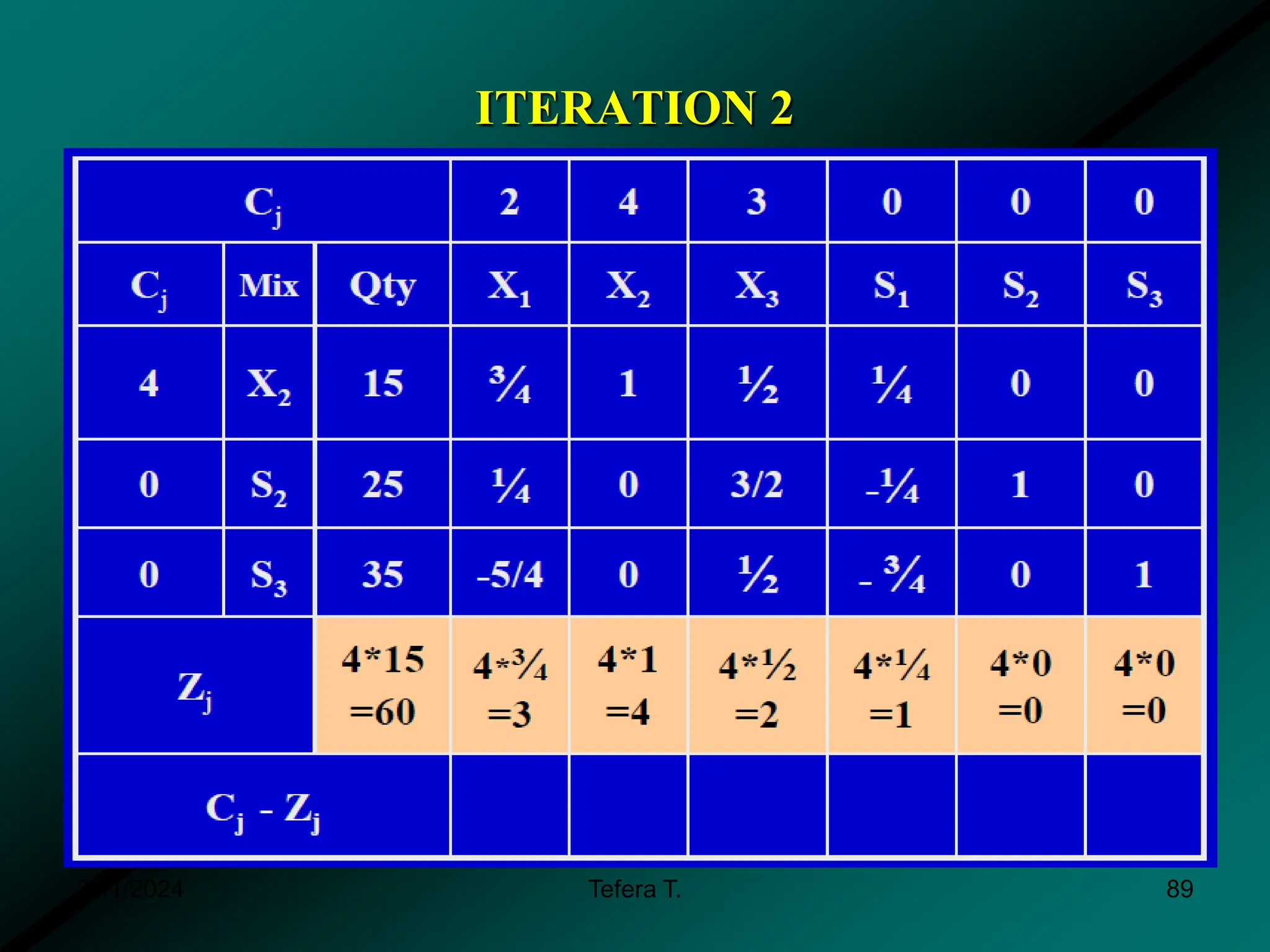
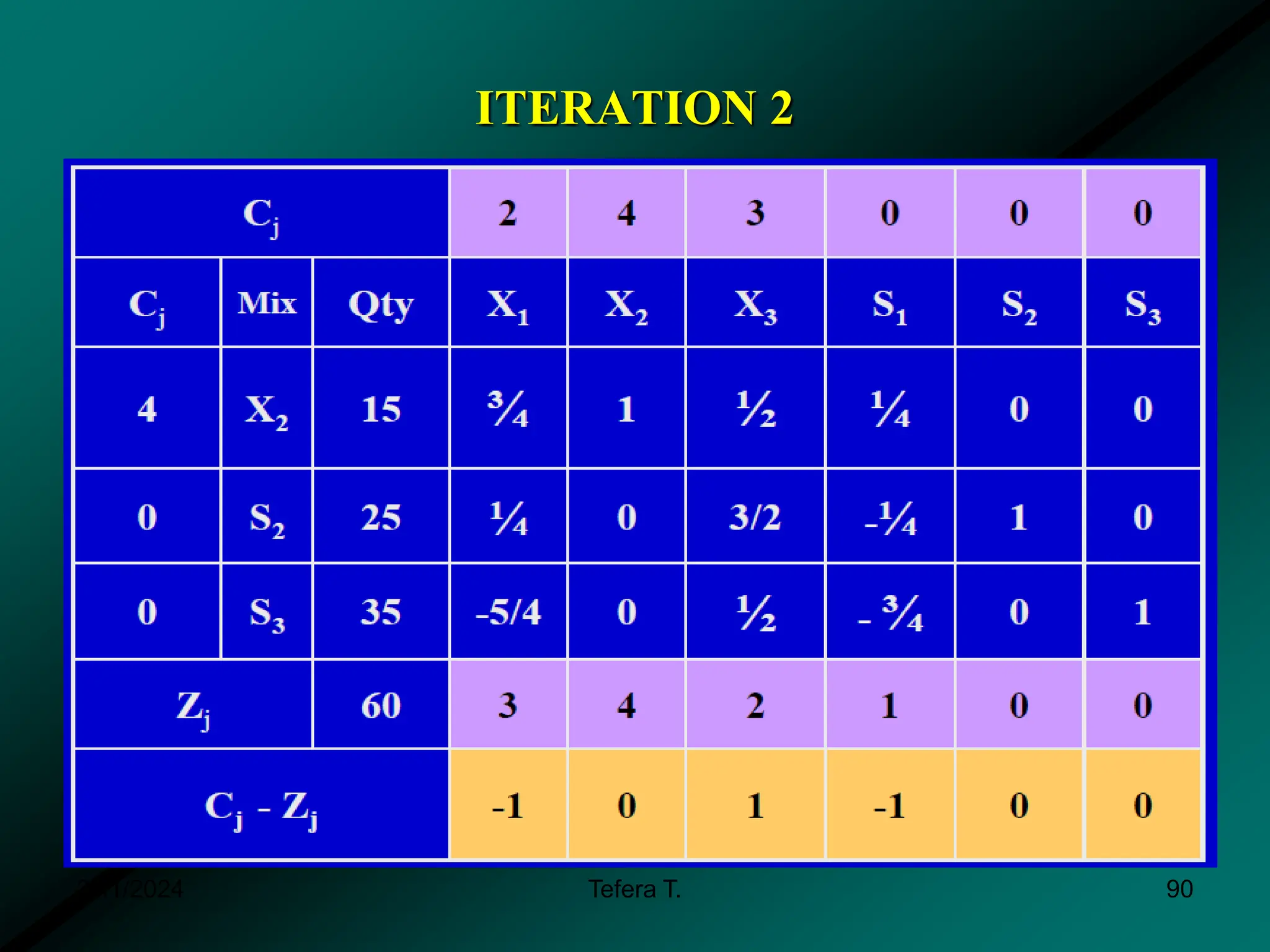
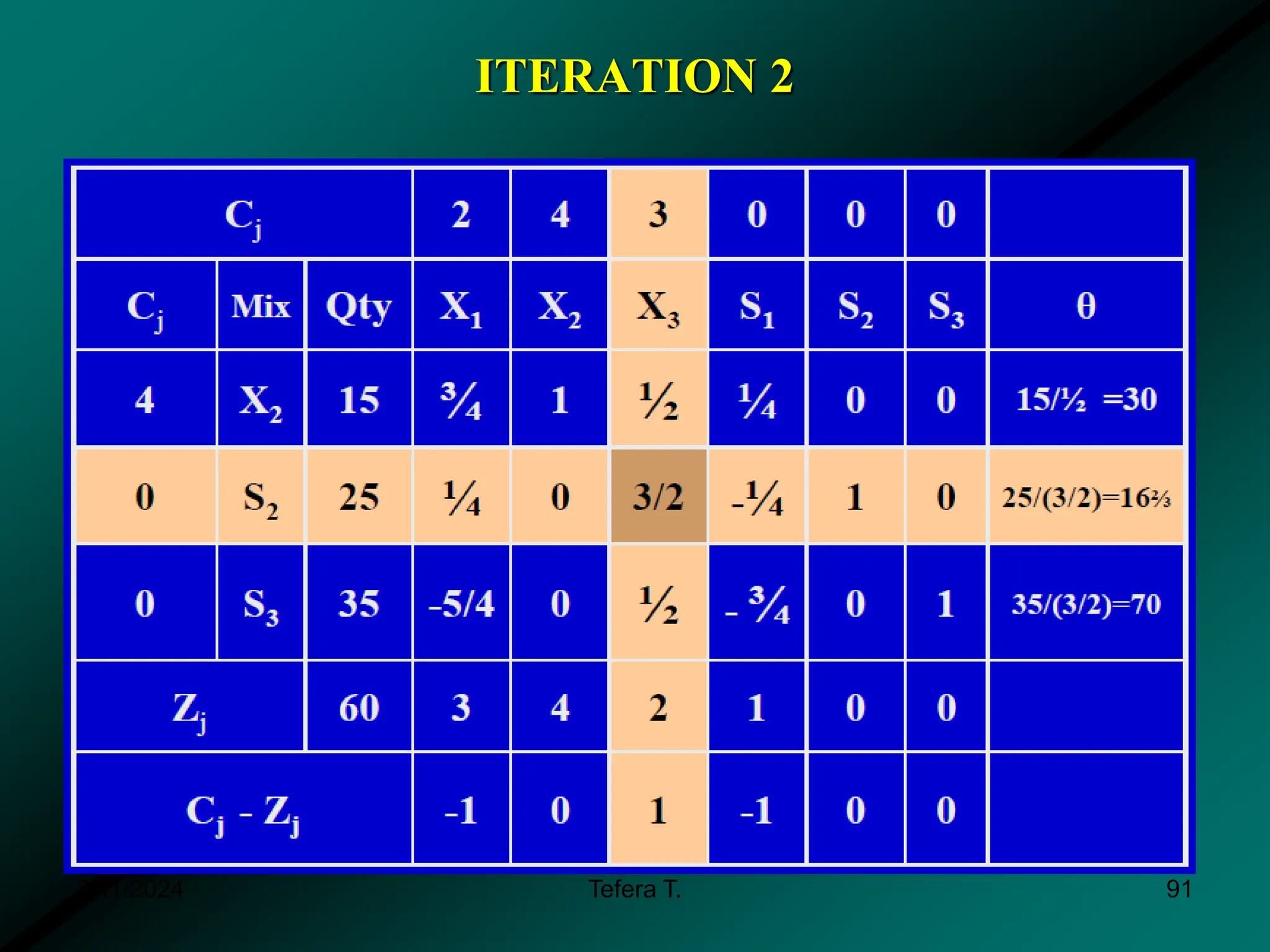
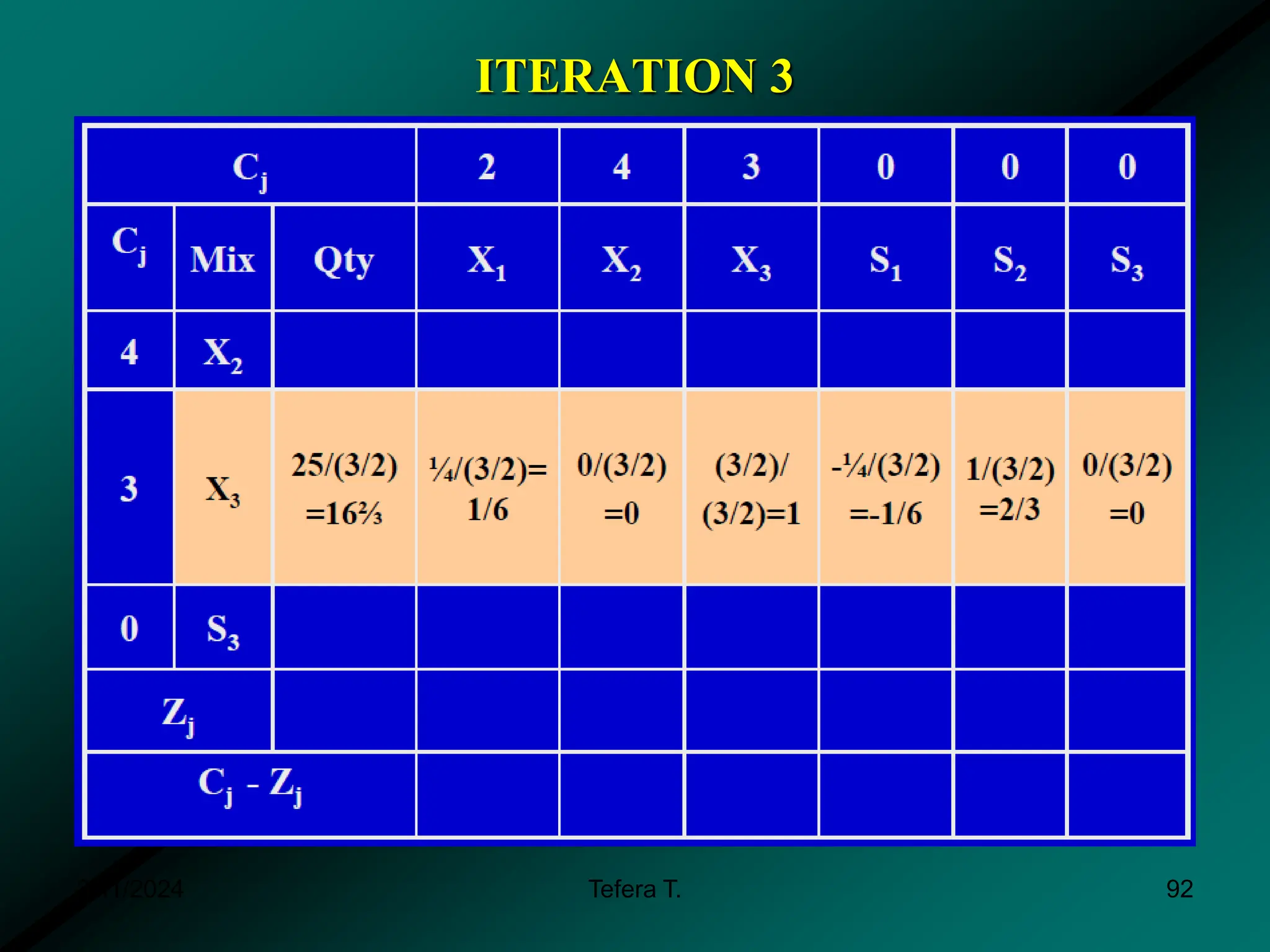
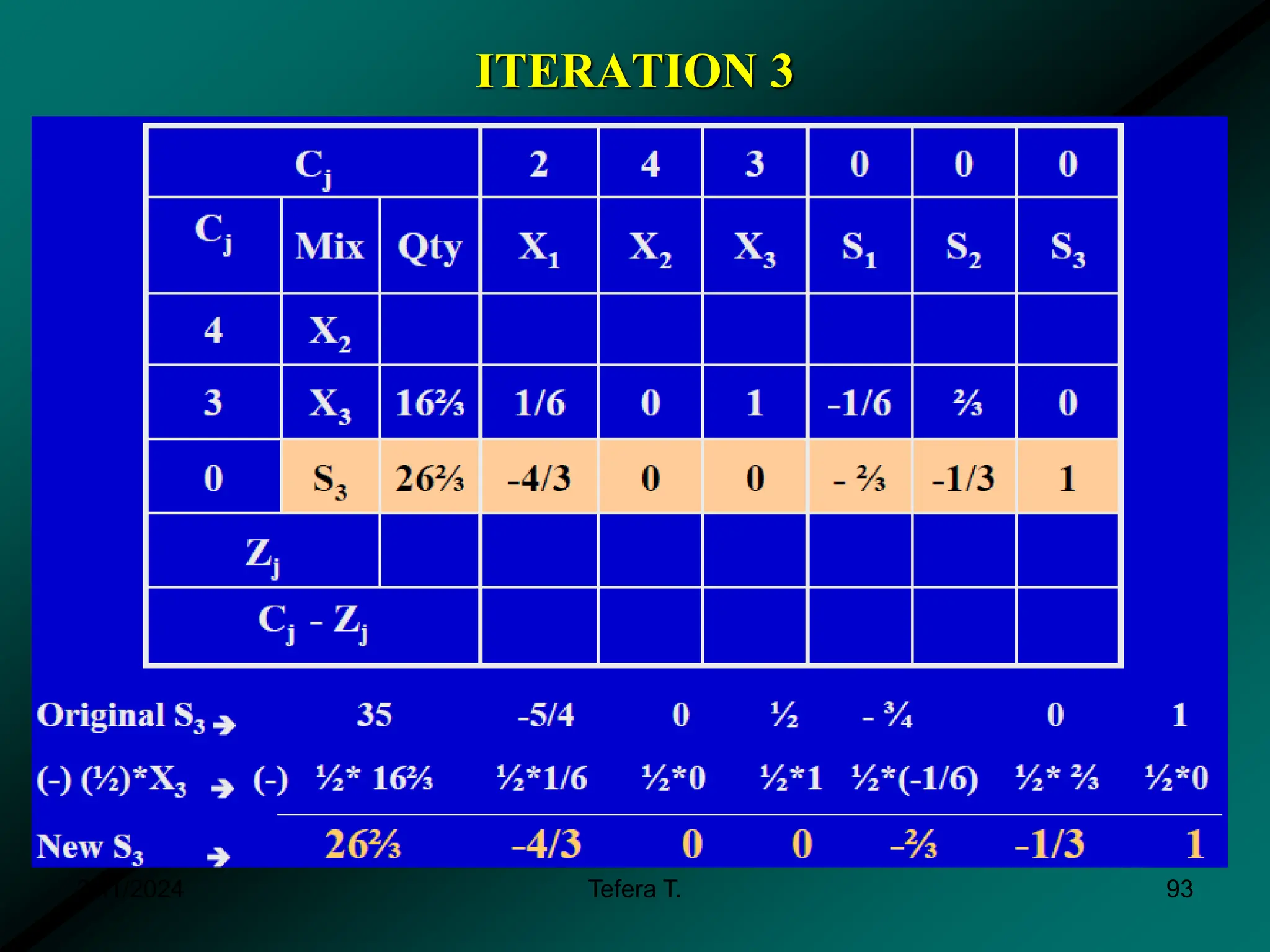
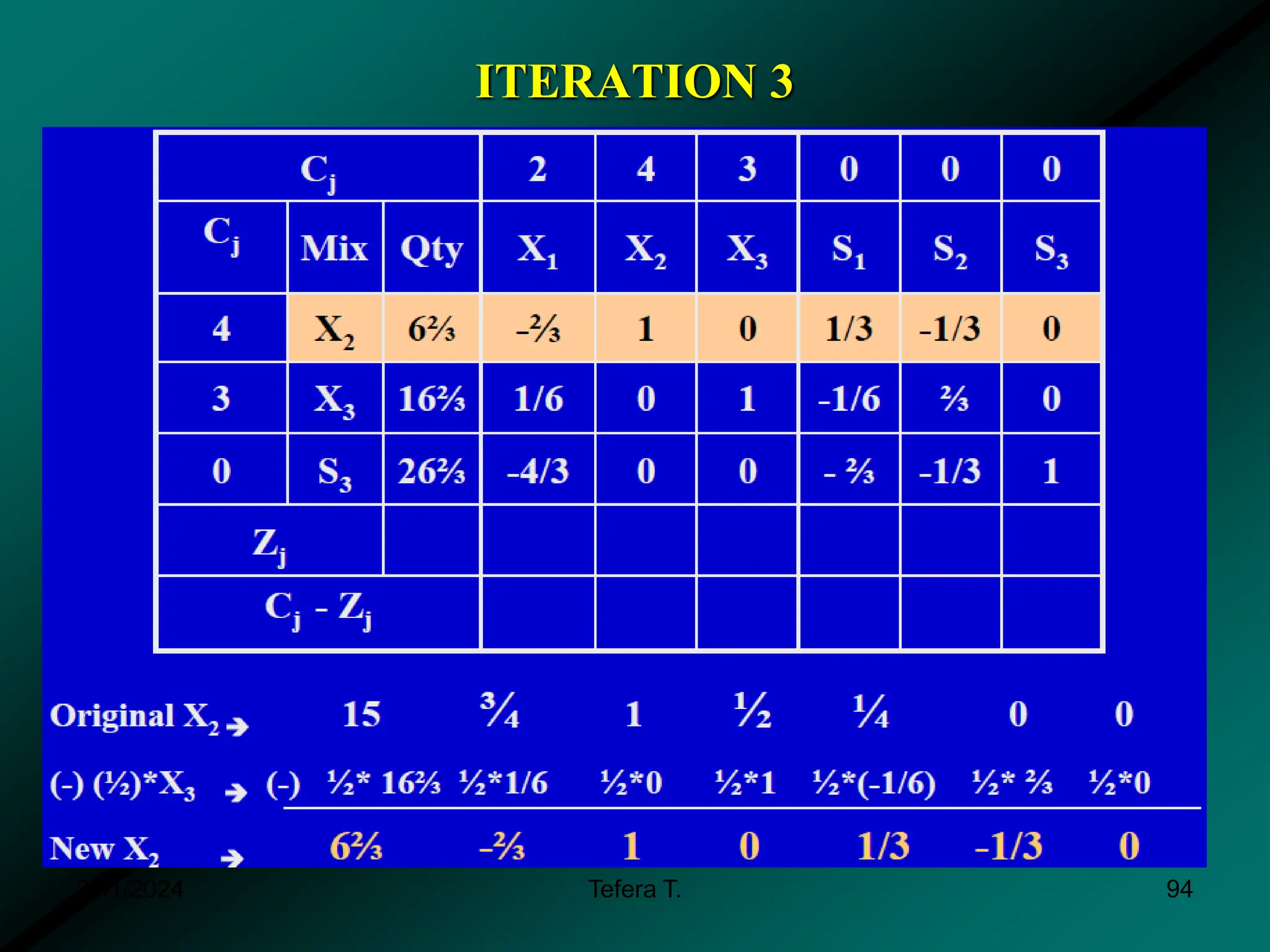
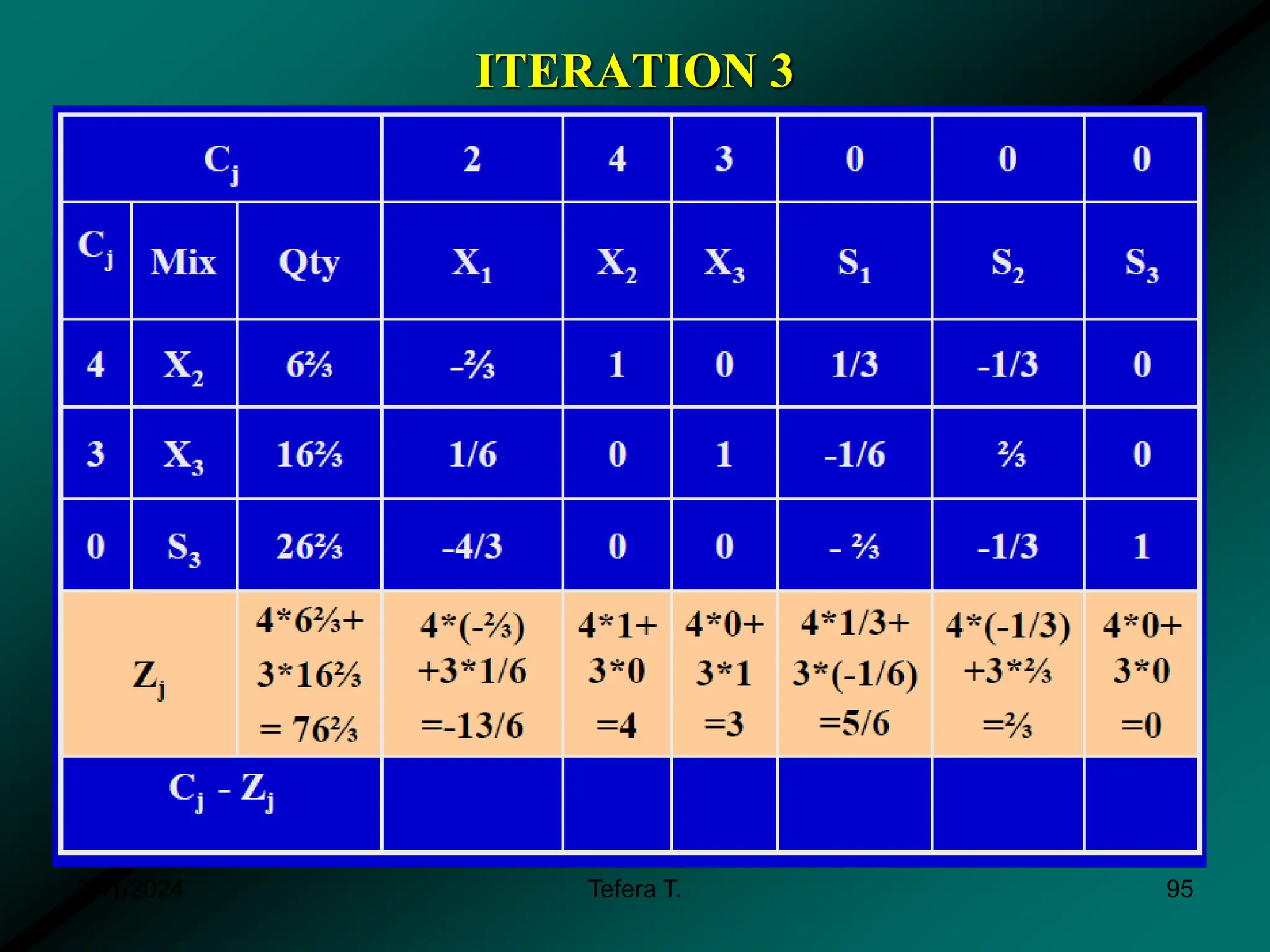
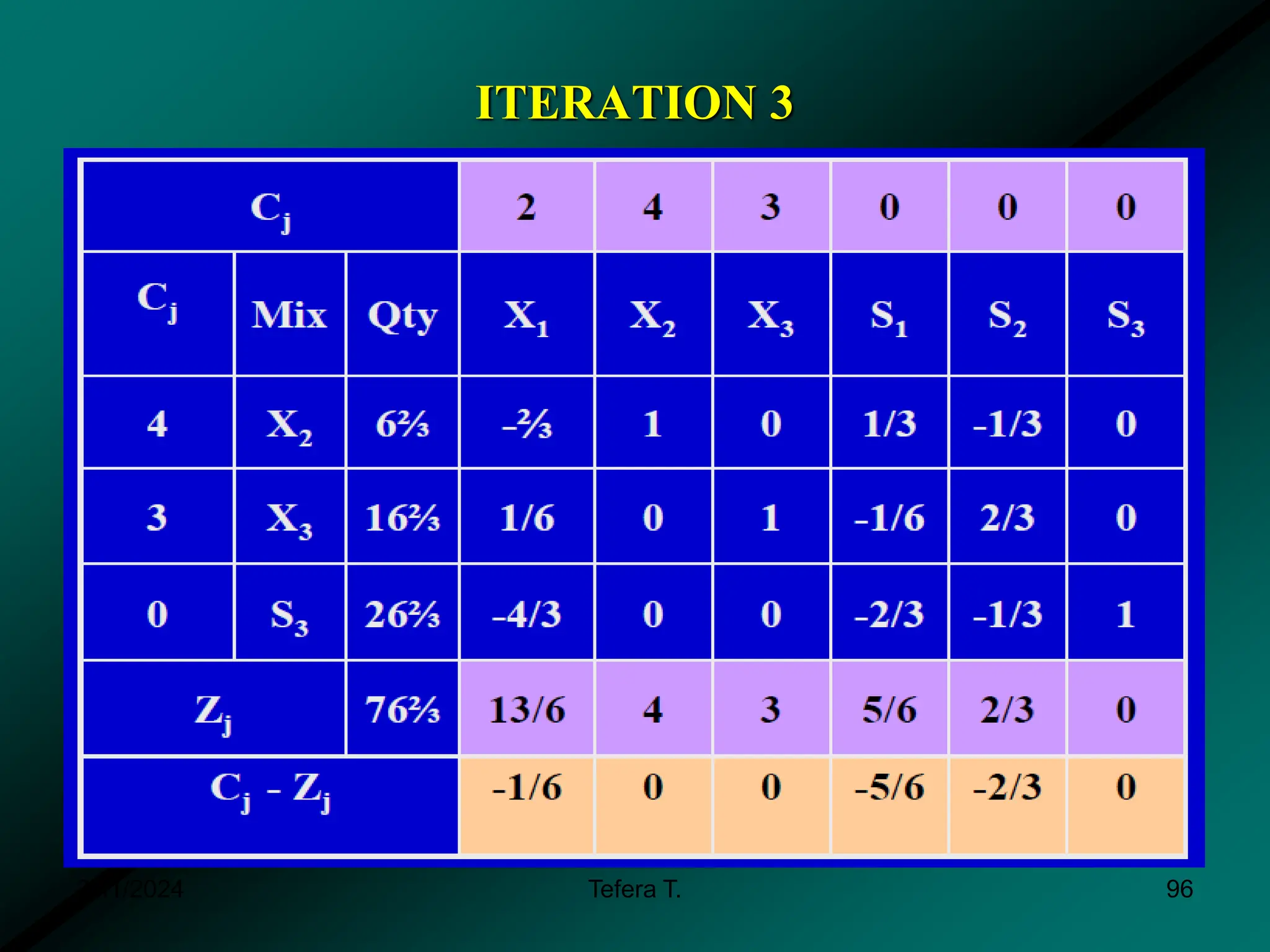
The document provides a detailed examination of the simplex method, a linear programming algorithm used for solving optimization problems with multiple decision variables. It outlines the technique's iterative process involving tableaus, optimality tests for both maximization and minimization problems, and the procedure for handling constraints. Additionally, it includes practical examples illustrating the setup and execution of the simplex algorithm in production problem scenarios.

1. Linear Programming II : Simplex Algorithm
Chapter Three
✦ Introduction
✦ Simplex method
✦ Solution of maximization
problems
✦ Solution of minimization
problems
✦ Some special topics
3/11/2024 1
Tefera T.

2. The Simplex Method
 Simplex: a linear-programming algorithm that can solve
problems having more than two decision variables.
✦ The simplex technique involves generating a series of
solutions in tabular form, called tableaus.
✦ By inspecting the bottom row of each tableau, one can
immediately tell if it represents the optimal solution.
✦ Each tableau corresponds to a corner point of the feasible
solution space.
✦ The first tableau corresponds to the origin . Subsequent
tableaus are developed by shifting to an adjacent corner
point in the direction that yields the highest (smallest) rate
of profit (cost). This process continues as long as a positive
(negative) rate of cost (profit ) exists.
3/11/2024 2
Tefera T.

3. The key solution concepts in simplex
 Solution Concept 1: The simplex method focuses on CPF
solutions.
 Solution concept 2: The simplex method is an iterative
algorithm (a systematic solution procedure that keeps
repeating a fixed series of steps, called, an iteration, until a
desired result has been obtained) with the following
structure:
 Solution concept 3: Whenever possible, the initialization of
the simplex method chooses the origin point (all decision
variables equal zero) to be the initial CPF solution.
3/11/2024 Tefera T. 3

4. Simplex algorithm
3/11/2024 Tefera T. 4
Initialization: Setup to start iterations, including
finding an initial CPF solution.
Optimality test: is the current CPF solution
optimal?
if no if yes stop
Iteration: Perform an iteration to find a
better CFP solution

5. Simplex algorithm
 Solution concept 4: Given a CPF solution, it is much
quicker computationally to gather information about its
adjacent CPF solutions than about other CPF solutions.
✦ Therefore, each time the simplex method performs an
iteration to move from the current CPF solution to a better
one, it always chooses a CPF solution that is adjacent to the
current one.
 Solution concept 5: After the current CPF solution is
identified, the simplex method examines each of the edges of
the feasible region that emanate from this CPF solution.
✦ Each of these edges leads to an adjacent CPF solution at the
other end, but the simplex method doesn’t even take the
time to solve for the adjacent CPF solution.
3/11/2024 Tefera T. 5

6. Procedure for handling Constraints
3/11/2024 Tefera T. 7

7. Cont..
3/11/2024 Tefera T. 8
Test for optimality:
Case 1: Maximization problem
 The current BF solution is optimal if the last row is
negative.(<=0)
Case 2: Minimization problem
The current BF solution is optimal if the last row is
positive.(>=0)
1. New pivot row = old pivot row  pivot number
2. For the other row apply this rule:
New row = old row – the coefficient of this row in the
pivot column*(new pivot row).

8. The Simplex Method of Linear Programming
Steps
 Express the objective function as an
equation.
 Set up the Constraint inequalities.
 Convert the inequalities to equations by
adding slack variables.
 Finally, add zero value variables so that all
variables appear in all equations.
3/11/2024 Tefera T. 9

9. Simplex Method
3/11/2024 Tefera T. 10
A. Qty. of each Variable
B. List of all Variables
C. Contribution per Unit of each Variable in Profit Equation
D. Relationship
E. Accounting for Transaction

10. 3/11/2024 Tefera T. 11
The Simplex Method:
Standard maximization Problems

11. A Standard Linear Programming Problem
 A standard maximization problem is one in
which
1. The objective function is to be maximized.
2. All the variables involved in the problem are
nonnegative.
3. All other linear constraints may be written so
that the expression involving the variables is less
than or equal to a nonnegative constant.
3/11/2024 12
Tefera T.

12. Setting Up the Initial Simplex Tableau
1. Transform the system of linear inequalities
into a system of linear equations by
introducing slack variables.
2. Rewrite the objective function
in the form
where all the variables are on the left and the
coefficient of P is +1. Write this equation
below the equations in step 1.
3. Write the augmented matrix associated with
this system of linear equations.
1 1 2 2 n n
P c x c x c x
  
1 1 2 2 0
n n
c x c x c x P
    
3/11/2024 13
Tefera T.

13. Applied Example 1: A Production Problem
 Recall the production problem discussed in chapter 1,
which required us to maximize the objective function
subject to the system of inequalities
 This is a standard maximization problem and may be
solved by the simplex method.
 Set up the initial simplex tableau for this linear
programming problem.
, 0
x y 
6
1.2
5
P x y P x y
   
or equivalently,
3 300
x y
 
2 180
x y
 
3/11/2024 14
Tefera T.

14. Applied Example 1: A Production Problem
Solution
 First, introduce the slack variables s1 and s2 into the
inequalities
and turn these into equations, getting
2x + y + s1 + 0s2 = 180
X + 3y + 0s1 + s2 = 300
 Next, rewrite the objective function in the form
3 300
x y
 
2 180
x y
 
6
0
5
x y P
   
3/11/2024 15
Tefera T.

15. Applied Example 1: A Production Problem
Solution
 Placing the restated objective function below the system of
equations of the constraints we get
2x + y + s1 + 0s2 = 180
X + 3y + 0s1 + s2 = 300
- x- 6/5y + 0s1 + 0s2 = 0
 Thus, the initial tableau associated with this system is
x y s1 s2 P Constant
2 1 1 0 0 180
1 3 0 1 0 300
–1 – 6/5 0 0 1 0
3/11/2024 16
Tefera T.

16. The Simplex Method
1. Set up the initial simplex tableau.
2. Determine whether the optimal solution has
been reached by examining all entries in the last
row to the left of the vertical line.
a. If all the entries are nonnegative, the optimal
solution has been reached. Proceed to step 4.
b. If there are one or more negative entries, the
optimal solution has not been reached.
Proceed to step 3.
3. Perform the pivot operation. Return to step 2.
4. Determine the optimal solution(s).
3/11/2024 17
Tefera T.

17. Applied Example 1: A Production Problem
 Recall again the production problem discussed previously.
 We have already performed step 1 obtaining the initial
simplex tableau:
 Now, complete the solution to the problem.
x y s1 s2 P Constant
2 1 1 0 0 180
1 3 0 1 0 300
–1 – 6/5 0 0 1 0
3/11/2024 18
Tefera T.

18. Applied Example 1: A Production Problem
Solution
Step 2. Determine whether the optimal solution has been
reached.
✦ Since there are negative entries in the last row of the
tableau, the initial solution is not optimal.
x y s1 s2 P Constant
2 1 1 0 0 180
1 3 0 1 0 300
–1 – 6/5 0 0 1 0
3/11/2024 19
Tefera T.

19. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Since the entry – 6/5 is the most negative entry to the left
of the vertical line in the last row of the tableau, the
second column in the tableau is the pivot column.
x y s1 s2 P Constant
2 1 1 0 0 180
1 3 0 1 0 300
–1 – 6/5 0 0 1 0
3/11/2024 20
Tefera T.

20. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Divide each positive number of the pivot column into the
corresponding entry in the column of constants and
compare the ratios thus obtained.
✦ We see that the ratio 300/3 = 100 is less than the ratio
180/1 = 180, so row 2 is the pivot row.
x y s1 s2 P Constant
2 1 1 0 0 180
1 3 0 1 0 300
–1 – 6/5 0 0 1 0
180
1
300
3
180
100


3/11/2024 21
Tefera T.

21. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ The entry 3 lying in the pivot column and the pivot row
is the pivot element.
x y s1 s2 P Constant
2 1 1 0 0 180
1 3 0 1 0 300
–1 – 6/5 0 0 1 0
3/11/2024 22
Tefera T.

22. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
1
2
3 R
x y s1 s2 P Constant
2 1 1 0 0 180
1 3 0 1 0 300
–1 – 6/5 0 0 1 0
3/11/2024 23
Tefera T.

23. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
1
2
3 R
x y s1 s2 P Constant
2 1 1 0 0 180
1/3 1 0 1/3 0 100
–1 – 6/5 0 0 1 0
3/11/2024 24
Tefera T.

24. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
1 2
6
3 2
5
R R
R R


x y s1 s2 P Constant
2 1 1 0 0 180
1/3 1 0 1/3 0 100
–1 – 6/5 0 0 1 0
3/11/2024 25
Tefera T.

25. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
1 2
6
3 2
5
R R
R R


x y s1 s2 P Constant
5/3 0 1 –1/3 0 80
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
3/11/2024 26
Tefera T.

26. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ This completes an iteration.
✦ The last row of the tableau contains a negative number,
so an optimal solution has not been reached.
✦ Therefore, we repeat the iteration step.
x y s1 s2 P Constant
5/3 0 1 –1/3 0 80
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
3/11/2024 27
Tefera T.

27. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation again.
✦ Since the entry – 3/5 is the most negative entry to the left
of the vertical line in the last row of the tableau, the first
column in the tableau is now the pivot column.
x y s1 s2 P Constant
5/3 0 1 –1/3 0 80
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
3/11/2024 28
Tefera T.

28. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Divide each positive number of the pivot column into the
corresponding entry in the column of constants and
compare the ratios thus obtained.
✦ We see that the ratio 80/(5/3) = 48 is less than the ratio
100/(1/3) = 300, so row 1 is the pivot row now.
x y s1 s2 P Constant
5/3 0 1 –1/3 0 80
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
80
5/3
100
1/3
48
300


Ratio
3/11/2024 29
Tefera T.

29. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ The entry 5/3 lying in the pivot column and the pivot
row is the pivot element.
x y s1 s2 P Constant
5/3 0 1 –1/3 0 80
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
3/11/2024 30
Tefera T.

30. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
x y s1 s2 P Constant
5/3 0 1 –1/3 0 80
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
3
1
5 R
3/11/2024 31
Tefera T.

31. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
x y s1 s2 P Constant
1 0 3/5 –1/5 0 48
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
3
1
5 R
3/11/2024 32
Tefera T.

32. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
1
2 1
3
3
3 1
5
R R
R R


x y s1 s2 P Constant
1 0 3/5 –1/5 0 48
1/3 1 0 1/3 0 100
–3/5 0 0 2/5 1 120
3/11/2024 33
Tefera T.

33. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
1
2 1
3
3
3 1
5
R R
R R


x y s1 s2 P Constant
1 0 3/5 –1/5 0 48
0 1 –1/5 2/5 0 84
0 0 9/25 7/25 1 148 4/5
3/11/2024 34
Tefera T.

34. Applied Example 1: A Production Problem
Solution
Step 3. Perform the pivot operation.
✦ The last row of the tableau contains no negative
numbers, so an optimal solution has been reached.
x y s1 S2 P Constant
1 0 3/5 –1/5 0 48
0 1 –1/5 2/5 0 84
0 0 9/25 7/25 1 148 4/5
3/11/2024 35
Tefera T.

35. Applied Example 1: A Production Problem
Solution
Step 4. Determine the optimal solution.
✦ Locate the basic variables in the final tableau.
In this case, the basic variables are x, y, and P.
 The optimal value for x is 48.
 The optimal value for y is 84.
 The optimal value for P is 148.8.
✦ Thus, the firm will maximize profits at $148.80 by
producing 48 type-A cement and 84 type-B cement .
This agrees with the results obtained in chapter one.
x y s1 s2 P Constant
1 0 3/5 –1/5 0 48
0 1 –1/5 2/5 0 84
0 0 9/25 7/25 1 148 4/5
3/11/2024 36
Tefera T.

36. The Simplex Method:
Standard Minimization Problems
3/11/2024 37
Tefera T.

37. Minimization with  Constraints
 In the last section we developed the simplex method to
solve linear programming problems that satisfy three
conditions:
1. The objective function is to be maximized.
2. All the variables involved are nonnegative.
3. Each linear constraint may be written so that the
expression involving the variables is less than or equal to
a nonnegative constant.
 We will now see how the simplex method can be used to
solve minimization problems that meet the second and
third conditions listed above.
3/11/2024 38
Tefera T.

38. Example
 Solve the following linear programming problem:
 This problem involves the minimization of the objective
function and so is not a standard maximization problem.
 Note, however, that all the other conditions for a standard
maximization hold true.
2 3
Minimize C x y
  
5 4 32
2 10
, 0
subject to x y
x y
x y
 
 

3/11/2024 39
Tefera T.

39. Example
 We can use the simplex method to solve this problem by
converting the objective function from minimizing C to its
equivalent of maximizing P = – C.
 Thus, the restated linear programming problem is
 This problem can now be solved using the simplex method
as discussed in chapter 1.
2 3
Maximize P x y
 
5 4 32
2 10
, 0
subject to x y
x y
x y
 
 

3/11/2024 40
Tefera T.

40. Example
Solution
Step 1. Set up the initial simplex tableau.
✦ Turn the constraints into equations adding to them the
slack variables u and v. Also rearrange the objective
function and place it below the constraints:
✦ Write the coefficients of the system in a tableau:
5 4 32
2 10
2 3 0
x y u
x y v
x y P
  
  
   
2 3
Maximize P x y
 
x y u v P Constant
5 4 1 0 0 32
1 2 0 1 0 10
–2 –3 0 0 1 0
3/11/2024 41
Tefera T.

41. Example
Solution
Step 2. Determine whether the optimal solution has been
reached.
✦ Since there are negative entries in the last row of the
tableau, the initial solution is not optimal.
x y u v P Constant
5 4 1 0 0 32
1 2 0 1 0 10
–2 –3 0 0 1 0
3/11/2024 42
Tefera T.

42. Example
Solution
Step 3. Perform the pivot operation.
✦ Since the entry – 3 is the most negative entry to the left
of the vertical line in the last row of the tableau, the
second column in the tableau is the pivot column.
2 3
Maximize P x y
 
x y u v P Constant
5 4 1 0 0 32
1 2 0 1 0 10
–2 –3 0 0 1 0
3/11/2024 43
Tefera T.

43. Example
Solution
Step 3. Perform the pivot operation.
✦ Divide each positive number of the pivot column into the
corresponding entry in the column of constants and
compare the ratios thus obtained.
✦ We see that the ratio 10/2 = 5 is less than the ratio
32/4 = 8, so row 2 is the pivot row.
2 3
Maximize P x y
 
32
4
10
2
8
5


x y u v P Constant
5 4 1 0 0 32
1 2 0 1 0 10
–2 –3 0 0 1 0
Ratio
3/11/2024 44
Tefera T.

44. Example
Solution
Step 3. Perform the pivot operation.
✦ The entry 2 lying in the pivot column and the pivot row
is the pivot element.
2 3
Maximize P x y
 
x y u v P Constant
5 4 1 0 0 32
1 2 0 1 0 10
–2 –3 0 0 1 0
3/11/2024 45
Tefera T.

45. Example
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
2 3
Maximize P x y
 
x y u v P Constant
5 4 1 0 0 32
1 2 0 1 0 10
–2 –3 0 0 1 0
1
2
2 R
3/11/2024 46
Tefera T.

46. Example
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
2 3
Maximize P x y
 
x y u v P Constant
5 4 1 0 0 32
1/2 1 0 1/2 0 5
–2 –3 0 0 1 0
1
2
2 R
3/11/2024 47
Tefera T.

47. Example
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
2 3
Maximize P x y
 
1 2
3 2
4
3
R R
R R


x y u v P Constant
5 4 1 0 0 32
1/2 1 0 1/2 0 5
–2 –3 0 0 1 0
3/11/2024 48
Tefera T.

48. Example
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
2 3
Maximize P x y
 
1 2
3 2
4
3
R R
R R


x y u v P Constant
3 0 1 –2 0 12
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
3/11/2024 49
Tefera T.

49. Example
Solution
Step 3. Perform the pivot operation.
✦ This completes an iteration.
✦ The last row of the tableau contains a negative number,
so an optimal solution has not been reached.
✦ Therefore, we repeat the iteration step.
2 3
Maximize P x y
 
x y u v P Constant
3 0 1 –2 0 12
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
3/11/2024 50
Tefera T.

50. Example
Solution
Step 3. Perform the pivot operation.
✦ Since the entry –1/2 is the most negative entry to the left
of the vertical line in the last row of the tableau, the first
column in the tableau is now the pivot column.
2 3
Maximize P x y
 
x y u v P Constant
3 0 1 –2 0 12
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
3/11/2024 51
Tefera T.

51. Example
Solution
Step 3. Perform the pivot operation.
✦ Divide each positive number of the pivot column into the
corresponding entry in the column of constants and
compare the ratios thus obtained.
✦ We see that the ratio 12/3 = 4 is less than the ratio
5/(1/2) = 10, so row 1 is now the pivot row.
2 3
Maximize P x y
 
x y u v P Constant
3 0 1 –2 0 12
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
12
3
5
1/2
4
10


3/11/2024 52
Tefera T.

52. Example
Solution
Step 3. Perform the pivot operation.
✦ The entry 3 lying in the pivot column and the pivot row
is the pivot element.
x y u v P Constant
3 0 1 –2 0 12
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
3/11/2024 53
Tefera T.

53. Example
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
x y u v P Constant
3 0 1 –2 0 12
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
1
1
3 R
3/11/2024 54
Tefera T.

54. Example
Solution
Step 3. Perform the pivot operation.
✦ Convert the pivot element into a 1.
x y u v P Constant
1 0 1/3 –2/3 0 4
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
1
1
3 R
3/11/2024 55
Tefera T.

55. Example
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
1
2 1
2
1
3 1
2
R R
R R


x y u v P Constant
1 0 1/3 –2/3 0 4
1/2 1 0 1/2 0 5
–1/2 0 0 3/2 1 15
3/11/2024 56
Tefera T.

56. Example
Solution
Step 3. Perform the pivot operation.
✦ Use elementary row operations to convert the pivot
column into a unit column.
1
2 1
2
1
3 1
2
R R
R R


x y u v P Constant
1 0 1/3 –2/3 0 4
0 1 –1/6 5/6 0 3
0 0 1/6 7/6 1 17
3/11/2024 57
Tefera T.

57. Example
Solution
Step 3. Perform the pivot operation.
✦ The last row of the tableau contains no negative
numbers, so an optimal solution has been reached.
x y u v P Constant
1 0 1/3 –2/3 0 4
0 1 –1/6 5/6 0 3
0 0 1/6 7/6 1 17
3/11/2024 58
Tefera T.

58. Example
Solution
Step 4. Determine the optimal solution.
✦ Locate the basic variables in the final tableau.
In this case, the basic variables are x, y, and P.
 The optimal value for x is 4.
 The optimal value for y is 3.
 The optimal value for P is 17, which means that
the minimized value for C is –17.
x y u v P Constant
1 0 1/3 –2/3 0 4
0 1 –1/6 5/6 0 3
0 0 1/6 7/6 1 17
3/11/2024 59
Tefera T.

59. The Dual Problem
 Another special class of linear programming problems we
encounter in practical applications is characterized by the
following conditions:
1. The objective function is to be minimized.
2. All the variables involved are nonnegative.
3. All other linear constraints may be written so that the
expression involving the variables is greater than or
equal to a nonnegative constant.
 Such problems are called standard minimization
problems.
3/11/2024 60
Tefera T.

60. The Dual Problem
 In solving this kind of linear programming problem, it
helps to note that each maximization problem is associated
with a minimization problem, and vice versa.
 The given problem is called the primal problem, and the
related problem is called the dual problem.
3/11/2024 61
Tefera T.

61. Example
 Write the dual problem associated with this problem:
 We first write down a tableau for the primal problem:
6 8
Minimize C x y
 
40 10 2400
10 15 2100
5 15 1500
, 0
subject to x y
x y
x y
x y
 
 
 

x y Constant
40 10 2400
10 15 2100
5 15 1500
6 8
Primal
Problem
3/11/2024 62
Tefera T.

62. Example
 Next, we interchange the columns and rows of the tableau
and head the three columns of the resulting array with the
three variables u, v, and w, obtaining
x y Constant
40 10 2400
10 15 2100
5 15 1500
6 8
u v w Constant
40 10 5 6
10 15 15 8
2400 2100 1500
3/11/2024 63
Tefera T.

63. Example
 Consider the resulting tableau as if it were the initial
simplex tableau for a standard maximization problem.
 From it we can reconstruct the required dual problem:
u v w Constant
40 10 5 6
10 15 15 8
2400 2100 1500
2400 2100 1500
Maximize P u v w
  
40 10 5 6
10 15 15 8
, , 0
subject to u v w
u v w
u v w
  
  

Dual
Problem
3/11/2024 64
Tefera T.

64. Theorem 1
The Fundamental Theorem of Duality
 A primal problem has a solution if and only if the
corresponding dual problem has a solution.
 Furthermore, if a solution exists, then:
a. The objective functions of both the primal and
the dual problem attain the same optimal value.
b. The optimal solution to the primal problem
appears under the slack variables in the last row
of the final simplex tableau associated with the
dual problem.
3/11/2024 65
Tefera T.

65. Example
 Complete the solution of the problem from our last example:
2400 2100 1500
Maximize P u v w
  
40 10 5 6
10 15 15 8
, , 0
subject to u v w
u v w
u v w
  
  

Dual
Problem
3/11/2024 66
Tefera T.

66. Example
Solution
 The dual problem associated with the given primal
problem is a standard maximization problem.
 Thus, we can proceed with the simplex method.
 First, we introduce to the system of equations the slack
variables x and y, and restate the inequalities as equations,
obtaining
40 10 5 6
10 15 15 8
2400 2100 1500 0
u v w x
u v w y
u v w P
   
   
    
3/11/2024 67
Tefera T.

67. Example
Solution
 Next, we transcribe the coefficients of the system of
equations
into an initial simplex tableau:
40 10 5 6
10 15 15 8
2400 2100 1500 0
u v w x
u v w y
u v w P
   
   
    
u v w x y P Constant
40 10 5 1 0 0 6
10 15 15 0 1 0 8
–2400 –2100 –1500 0 0 1 0
3/11/2024 68
Tefera T.

68. Example
Solution
 Continue with the simplex iterative method until a final
tableau is obtained with the solution for the problem:
 The fundamental theorem of duality tells us that the
solution to the primal problem is x = 30 and y = 120, with a
minimum value for C of 1140.
u v w x y P Constant
1 0 –3/20 3/100 –1/50 0 1/50
0 1 11/10 –1/50 2/25 0 13/25
0 0 450 30 120 1 1140
Solution for the
primal problem
3/11/2024 69
Tefera T.

69. 3/11/2024 70
Tefera T.

70. Examples
3/11/2024 Tefera T. 71

71. The Simplex Method of Linear Programming
Example 1
 Objective Function : Maximize Z = 5 X1 + 6 X2
subject to 3X1 + 2X2 ≤ 32
X1 + 4X2 ≤ 34
✦Maximize Z = 5X1 + 6X2 + 0S1 + 0S2
✦Con1. 3X1 + 2X2 +1S1 + 0S2 = 32
✦Con 2. X1 + 4X2 +0S1 + 1S2 = 34
3/11/2024 Tefera T. 72

72. ITERATION1
3/11/2024 Tefera T. 73
Simplex criteria

73. ITERATION 2
3/11/2024 Tefera T. 74

74. ITERATION 2
3/11/2024 Tefera T. 75

75. ITERATION 2
3/11/2024 Tefera T. 76

76. ITERATION 2
3/11/2024 Tefera T. 77

77. ITERATION 2
3/11/2024 Tefera T. 78

78. ITERATION 3
3/11/2024 Tefera T. 79

79. ITERATION 3
3/11/2024 Tefera T. 80

80. ITERATION 3
3/11/2024 Tefera T. 81

81. ITERATION 3
3/11/2024 Tefera T. 82

82. ITERATION 3-
Optimal solution
3/11/2024 Tefera T. 83

83. The Simplex Method of Linear Programming
Example 2
3/11/2024 Tefera T. 84

84. ITERATION 1
3/11/2024 Tefera T. 85

85. ITERATION 2
3/11/2024 Tefera T. 86

86. ITERATION 2
3/11/2024 Tefera T. 87

87. ITERATION 2
3/11/2024 Tefera T. 88

88. ITERATION 2
3/11/2024 Tefera T. 89

89. ITERATION 2
3/11/2024 Tefera T. 90

90. ITERATION 2
3/11/2024 Tefera T. 91

91. ITERATION 3
3/11/2024 Tefera T. 92

92. ITERATION 3
3/11/2024 Tefera T. 93

93. ITERATION 3
3/11/2024 Tefera T. 94

94. ITERATION 3
3/11/2024 Tefera T. 95

95. ITERATION 3
3/11/2024 Tefera T. 96

96. ITERATION 3
3/11/2024 Tefera T. 97

97. 3/11/2024 Tefera T. 98