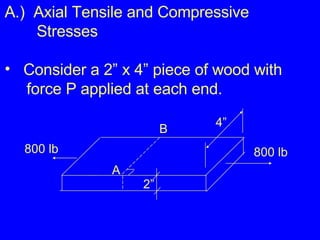
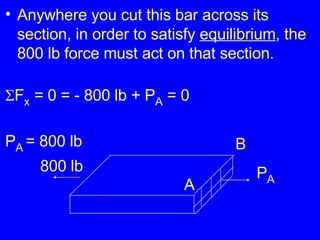
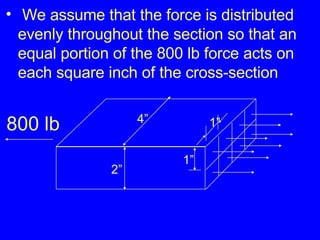
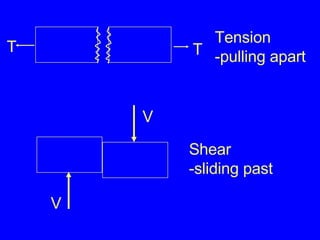
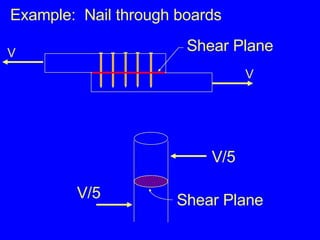
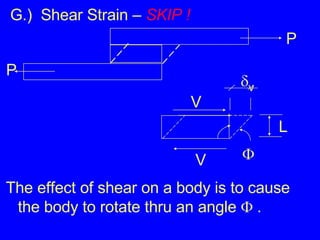
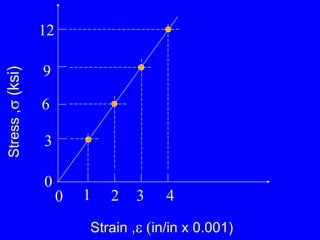
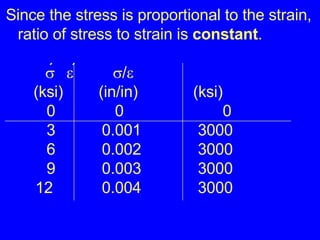
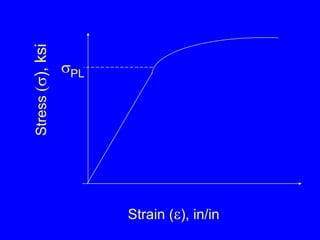
This document summarizes key concepts in stresses and strains from strength of materials including: 1) Definitions of stress as force per unit area and strain as deformation per original length. Common types of stress include axial/tensile, compressive, shear, and bearing stresses. 2) The proportional relationship between stress and strain for a material below its proportional limit, defined by modulus of elasticity E. Stress and strain can then be calculated from each other. 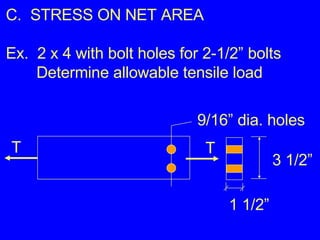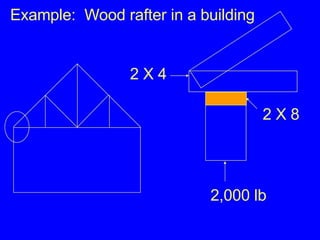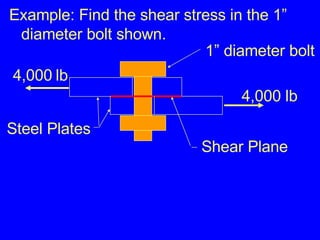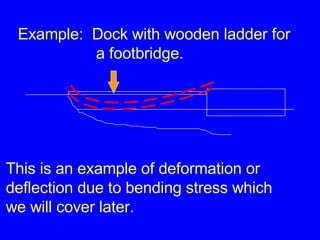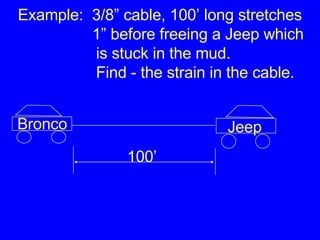3) Examples calculating stresses, strains, and deformations in axially loaded members and bolts, finding required member sizes, and checking stresses are below limits.

1. I) Stresses and Strains In statics we assumed rigid bodies In strength of materials, we acknowledge that bodies are deformable , not rigid. We will study the stresses applied forces produce in a body and the accompanying strains .

2. A.) Axial Tensile and Compressive Stresses Consider a 2” x 4” piece of wood with force P applied at each end. 800 lb 800 lb 2” 4” A B

3. Anywhere you cut this bar across its section, in order to satisfy equilibrium , the 800 lb force must act on that section.  F x = 0 = - 800 lb + P A = 0 P A = 800 lb P A 800 lb A B

4. We assume that the force is distributed evenly throughout the section so that an equal portion of the 800 lb force acts on each square inch of the cross-section 800 lb 2” 4” 1” 1”

5. Since we have 8 square makes, the amount of force on each square inch is: 800 lb = 100 lb = 100 psi 8in 2 in 2

6. Which is the definition of stress :  = P A  = stress = unit stress = average stress = engineering stress P = applied force A= constant cross-sectional area over which the stress develops

7.  t = Tensile Stress (produced by Tensile Forces)  c = Compressive Stress (produced by Compressive Forces)

8. Normal Stress = stress acting on a plane perpendicular to (or normal to) the line of action of the applied force (as in our example). we will discuss stresses on inclined planes in week 4.

9. B. TENSILE AND COMPRESSIVE STRESSES - Application 1.) Analyze the capacity of existing member P (all) =   (all) A A= cross-sectional area, perpendicular to the direction of the force

10. P (all) = axial load capacity (max allowable axial load) = amount of load the member can safely carry  (all) = allowable axial stress=amount of stress which is judged acceptable for the given material

11. Example: 2 x 4 wood with tensile force applied. Find the axial load capacity of the 2 x 4. A = 3.5” x 1.5” = 5.25in 2 ,  (all) = 400 psi  (all) = 400 psi P t(all) =  (all) A=(400 psi)(5.25in 2 ) = 2,100 lb

12. 2. Design a member to support a known load. A (req) = P_  (all) A (req) = required cross-sectional area of the axially loaded member being designed. P = applied axial load  (all) = allowable axial stress

13. Example: Find what diameter steel rod is required to support a 2100# tension force. P = 2100 lb  (all) = 24,000 psi (= lb/in 2 ) A (req) = P = 2,100 lb = .0875 in 2  (all) 24,000 lb/in 2 diameter = d 2100 lb 2100 lb

14. A (req) = .0875 in 2 =  (r) 2 =  (d req ) 2 4 (d req ) 2 = .0875 in 2 (4) = 0.1114 in 2    d req =(0.1114 in 2 ) 1/2 = .333” = 3/8”  Therefore a 3/8” diameter steel rod supports as much tensile force as 2” x 4”.

15. Note : App. A,B,C*,D* give cross-sectional areas for different steel shapes. E gives cross-sectional areas for lumber.

16. 3.) Cautions concerning design and analysis: a.) Some materials have a higher allowable compressive stress than tensile stress (  t(all) <  c(all) ) Examples: Wood, concrete, cast iron (refer to App. F, G, 722, 723)

17. b.) The length of a member effects how much compressive force it can sustain. Will discuss in depth in Week 14 (columns). C all < T all For now, we will assume compressive members are short enough to ignore effect of length.

18. c). Holes for bolts etc. must be subtracted from the gross cross-sectional area to obtain the net cross-sectional area (A net ). d.) Design Manuals have been published by Steel (AISC), Wood (AITC, NDS), Concrete (ACI), and Aluminum associations.

19. e.) Assuming even force distribution over the cross-sectional area is usually valid, but not always .

20. C. STRESS ON NET AREA Ex. 2 x 4 with bolt holes for 2-1/2” bolts Determine allowable tensile load 9/16” dia. holes 3 1/2” 1 1/2” T T

21. T all =  t,all A net  t(all) = 400 psi A net = A - A holes = (3.5” x 1.5”) - (2)(9/16”)(1.5”) = 3.56 in 2 T all = (400 psi)(3.56 in 2 ) = 1425 lb

22. Note : 3.5” and 1.5” are “dressed dimensions” (see APP.E) 2 x 4 is actually 1.5” x 3.5” 2 x 8 is actually 1.5” x 7.25”

23. D.) Bearing Stress (  p ) -A contact pressure between separate bodies. -A type of compressive stress

24. Example: Wood rafter in a building 2 X 4 2 X 8 2,000 lb

25.  p = P A bear P = 2000 lb A bear = 1 1/2” x 71/4” = 10.88 in 2  p = 2,000 lb = 184 psi 10.88 in 2

26. E.) Shear Stress Normal stress (tensile and compressive) acts in a direction perpendicular to the surface on which it acts. It is produced by a force whose line of action is perpendicular to the surface on which the stress is produced.

27. Shear stress acts in a direction parallel to the surface on which it acts. It is produced by a force whose line of action is parallel to the surface on which the stress is produced.

28. T T Tension -pulling apart V V Shear -sliding past

29. Example: Nail through boards Shear Plane V/5 V/5 V V Shear Plane

30.  v = V A  v = shear stress (psi) V = shear force (lb) A= cross-sectional area parallel to the force.

31. Example: Find the shear stress in the 1” diameter bolt shown. 1” diameter bolt 4,000 lb Steel Plates 4,000 lb Shear Plane

32.  v = V A V = 4,000 lb A =  d 2 =  (1”) 2 = .785 in 2 4 4  v = 4,000 lb = 5,096 psi .785 in 2

33. F.) TENSILE AND COMPRESSIVE STRAINS AND DEFORMATIONS In picking a member size, we not only need to know it can handle the load without failing due to too much stress (i.e. fracture or “break”), we must also be sure it will not deflect (or deform) excessively.

34. Example: Dock with wooden ladder for a footbridge. This is an example of deformation or deflection due to bending stress which we will cover later.

35. Similarly, when a steel rod is in Tension, it will deform, but it is not as noticeable.  = deformation = the amount a body is lengthened by a Tensile force and shortened by a compressive force. L  T T

36. To permit comparison with acceptable values, the deformation is usually converted to a unit basis, which is the strain .  =   L  = strain (= unit strain)  = deformation that occurs over length L L = original length of member

37. Example:

38. Example: 3/8” cable, 100’ long stretches 1” before freeing a Jeep which is stuck in the mud. Find - the strain in the cable. 100’ Jeep Bronco

39.  =   L  = 1” L = 100’ (12”/1) = 1200”  = 1” = 0.0008333 in/in 1200” We’ll come back to see if this is will break the cable.

40. G.) Shear Strain – SKIP ! The effect of shear on a body is to cause the body to rotate thru an angle  . P P L V V  v 

41. SKIP ! tan  =  v _ _ L  = shear strain (radians)  v = shear deformation (in) L = Distance over which shear deformation occurs (in)

42. SKIP ! Since  is always a very small angle, and for small angles: tan  =  Then:  =  v /L

43. Review of Stress and Strain Axial Stress and Strain  = P A  =  L  Shear Stress and Strain  = V_  A  =  v /L - SKIP !

44. H.) The Relationship Between Stress and Strain As you apply load to a material, the strain increases constantly (or proportionately) with stress.

45. Example: In a tension test you apply a gradually increasing load to a sample. You can determine the amount of strain (  that occurs in a sample at any given stress level (  .  (ksi)  (in/in) 0 0.000 3 0.001 6 0.002 9 0.003 12 0.004

46. Stress ,  (ksi) Strain ,  in/in x 0.001)           

47. Since the stress is proportional to the strain, ratio of stress to strain is constant .  /   (ksi)  (in/in)  (ksi) 0 0 0 3 0.001 3000 6 0.002 3000 9 0.003 3000 12 0.004 3000

48. This constant ratio of stress to strain is called the Modulus of Elasticity (E). E =  /  The Modulus of Elasticity is always the same for a given material (see p. 617). We call it a material constant .

49. Knowing E for a given material and : E =  /  1.) We can find how much stress is in the material if we know the strain:  = E  2.) We can find how much strain is in the material if we know the stress:  =  E

50. CAUTION ! If the tension test continues, the stress will reach a level called the Proportional Limit (  PL ). If the stress is increased above  PL , the strain will increase at a higher rate.

51.  Stress  ), ksi Strain (  ), in/in  PL

52. Strain is directly proportional to stress as long as the stress does not exceed the proportional limit (  PL ) of the material. That is:   = E = constant, ONLY if   PL  Anytime you use E to find stress or strain, you must check to make sure   PL .

53. Ex. Given: Previous Truck cable strain Find: Stress in the steel cable  = 1” L = 1200”  = 1” = 0.0008333 in/in 1200”   E ( as long as  PL )  E= 30,000,000 psi (for steel) 

54.  E  = 30,000,000 psi (.0008333 in/in) = 24,990 psi (pretty high) CHECK: is  <  PL ?  = 24,990 psi <  PL = 34,000 psi (OK)

55. For Shear Stress and Strains: G =  v = Modulus of Rigidity 

56. Substituting  = P and  =  A L into E =   Assuming  <  pL )  E = P/A  /L Note: E, G are constant

57. Solving for   = P L AE  = PL IF ,  <  PL AE

58. Example 2: How much will a 1” diameter by 150” long steel bar stretch if a 1000 lb axial tension load is applied to it ?  = P = 1000 lb = 1,273 psi <  Y  36,000 psi A  (0.5”) 2  =  = __1,273 psi___ = 0.00004244 in/in E 30,000,000 psi  L  0.00004244 in/in)(150”) = 0.006366 ”