Downloaded 722 times
Uploaded byReo Minao
Strategic intervention material
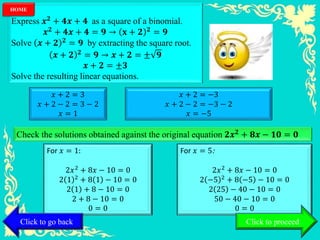
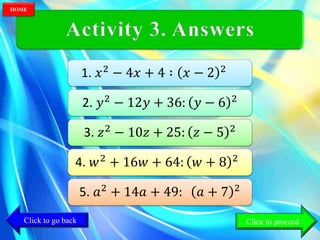This document provides instruction on solving quadratic equations by completing the square. It begins by defining a quadratic equation and explaining why the coefficient of the quadratic term cannot be zero. It then presents the steps to solve a quadratic equation by completing the square, which involves transforming the equation into the form (x - h)2 = k. An example problem is worked through to demonstrate the process.
More Related Content
Similar to Strategic intervention material
Strategic intervention material
- 1.
- 2. STRATEGIC INTERVENTION MATERIAL Prepared by: REORINA C.MINAO T-I Don Carlos National High School Sinanguyan, Don Carlos, Bukidnon STRATEGIC INTERVENTION MATERIAL (Computer-Based) Click to go back HOME Click to proceed
- 3. STRATEGIC INTERVENTION MATERIAL Solving Quadratic Equation byCompleting the Square Least Mastered Competency * Solving Quadratic Equation by Completing a Square Sub Tasks: *Identifying quadratic equation *Determining a perfect square trinomial *Expressing Perfect Square trinomial as a square of a binomial *Solving quadratic equation by completing the square. Click to go back HOME Click to proceed
- 4. GUIDE CARD A quadraticequation in one variable is a mathematical sentence of degree 2 that can be written in the following form; 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0, 𝑤ℎ𝑒𝑟𝑒 𝑎, 𝑏, 𝑎𝑛𝑑 𝑐 𝑎𝑟𝑒 𝑟𝑒𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑎𝑛𝑑 𝑎 ≠ 0. In the equation, 𝑎𝑥2, is the quadratic term, 𝑏𝑥 is the linear term, and 𝑐 is the constant term. Example: 2𝑥2 + 5x + 3 = 0 𝑎 = 2, 𝑏 = 5, 𝑐 = 3 Click to go back HOME Click to proceed
- 5. Activity 1. Quadraticor Not Determine the given expression as quadratic or not. Write Q if it quadratic and NQ if it is not. __________1. 𝑥 + 5 = −2 __________2. 𝑥2 − 5 = 𝑥 __________3. −2𝑥2 =0 __________4. 𝑥 − 10 = 3𝑥 __________5. 𝑥3 + 𝑥2 = −1 Click to go back HOME Click to proceed
- 6. On Quadratic Equation Aquadratic equation in one variable is a mathematical sentence of degree 2 that can be written in the following form; 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0, 𝑤ℎ𝑒𝑟𝑒 𝑎, 𝑏, 𝑎𝑛𝑑 𝑐 𝑎𝑟𝑒 𝑟𝑒𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑎𝑛𝑑 𝑎 ≠ 0. In the equation, 𝑎𝑥2 , is the quadratic term, 𝑏𝑥 is the linear term, and 𝑐 is the constant term. Why do you think a must not be equal to zero? Example: 2𝑥2 + 5x + 3 = 0 𝑎 = 2, 𝑏 = 5, 𝑐 = 3 Why do you think a must not be equal to zero? ans Click to go back HOME Click to proceed
- 7. 𝒂𝒙 𝟐 +𝒃𝒙 + 𝒄 = 𝟎 Substituting 𝒂 = 𝟎 in the equation will yield a linear equation. So 𝒂 must not be equal to zero 𝟎𝒙 𝟐 + 𝒃𝒙 + 𝒄 = 𝟎 𝒃𝒙 + 𝒄 = 𝟎 illustration The derived equation is in first degree Click to go back HOME
- 8. Activity 2: AmI a Perfect Square Trinomial or Not? Determine each of the following whether it is a perfect square trinomial or not. Write PST if it is a perfect square trinomial and NPST if it is not. _________1. 𝑥2 + 2𝑥 − 2 _________2. 𝑥2 + 4𝑥 + 4 _________3. 4𝑥2 − 8𝑥 + 2 _________4. 𝑥2 − 6𝑥 − 9 _________5. 2𝑥2 − 4𝑥 + 4 How do you describe a perfect square trinomial? How do you describe a perfect square trinomial? Click to go back HOME Click to proceed
- 9. Perfect Square Trinomial Firstand last terms are perfect square. Middle term is twice the product of the square root of the first and last terms. Example: 𝑥2 + 4𝑥 + 4 𝑚𝑖𝑑𝑑𝑙𝑒 𝑡𝑒𝑟𝑚 4𝑥 = 𝑥2 ∙ 4 first and last term (perfect squares) Click to go back HOME
- 10. Activity 3. TransformMe! Express each of the given trinomial as a square of a binomial. 1. 𝑥2 − 4𝑥 + 4 ∶ ___________ 2. 𝑦2 − 12𝑦 + 36: ___________ 3. 𝑧2 − 10𝑧 + 25: ___________ 4. 𝑤2 + 16𝑤 + 64: ___________ 5. 𝑎2 + 14𝑎 + 49: ______________ How to transform a PST to a square of a binomial? ans Click to go back HOME Click to proceed
- 11. Click to goback HOME
- 12. 1. 𝑥2 − 4𝑥+ 4 ∶ 𝑥 − 2 2 2. 𝑦2 − 12𝑦 + 36: 𝑦 − 6 2 3. 𝑧2 − 10𝑧 + 25: 𝑧 − 5 2 4. 𝑤2 + 16𝑤 + 64: 𝑤 + 8 2 5. 𝑎2 + 14𝑎 + 49: 𝑎 + 7 2 Click to go back HOME Click to proceed
- 13. How to solveQE using completing the square method? Another method of solving quadratic equation is by completing the square. This method involves transforming the quadratic equation 𝑎𝑥2 = 𝑏𝑥 + 𝑐 = 0 into the form (𝑥 − ℎ)2 = 𝑘, where 𝑘 ≥ 0. What are the steps in solving QE by completing the square? Click to go back HOME Click to proceed
- 14. Steps in solvingQE by completing the square 1. Divide both sides of the equation by a then simplify. 2. Write the equation such that the terms with variables are on the left side of the equation and the constant term is on the right side. 3. Add the square of one-half of the coefficient of x on both sides of the resulting equation. 4. Express the perfect square trinomial on the left side of the equation as a square of a binomial. What happens to the left side of the equation? ans Click to go back HOME Click to proceed
- 15. Click to goback HOME
- 16. Steps in solvingQE by completing the square: Cont… 5. Solve the resulting QE by extracting the square root. Add the square of one-half of the coefficient of x on both sides of the resulting equation. 6. Solve the resulting linear equation. 7. Check the solution obtained against the original equation. Click to go back HOME Click to proceed
- 17. Example: Solve thequadratic equation 𝑥2 + 3𝑥 − 10 = 0 by completing the square. Solution: Divide both sides of the equation by 2 then simplify. 2𝑥2 + 8x − 10 = 0 2𝑥2+8𝑥−10=0 2 =𝑥2 + 4𝑥 − 5 = 0 Add 5 to both sides of the equation, then simplify. 𝑥2 + 4𝑥 − 5 = 0 𝑥2 + 4𝑥 − 5 + 5 = 0 + 5 𝑥2 + 4𝑥 = 5 Add to both sides of the equation the square of one-half of 4. 1 2 4 = 2 22=4. 𝑥2 + 4𝑥 = 5 → 𝑥2 + 4𝑥 + 4 = 5 + 4 𝑥2 + 4𝑥 + 4 = 9 Click to go back HOME Click to proceed
- 18. Express 𝒙 𝟐+ 𝟒𝒙 + 𝟒 as a square of a binomial. 𝒙 𝟐 + 𝟒𝒙 + 𝟒 = 𝟗 → 𝐱 + 𝟐 𝟐 = 𝟗 Solve 𝒙 + 𝟐 𝟐 = 𝟗 by extracting the square root. 𝒙 + 𝟐 𝟐 = 𝟗 → 𝒙 + 𝟐 = ± 𝟗 𝒙 + 𝟐 = ±𝟑 Solve the resulting linear equations. 𝑥 + 2 = 3 𝑥 + 2 − 2 = 3 − 2 𝑥 = 1 𝑥 + 2 = −3 𝑥 + 2 − 2 = −3 − 2 𝑥 = −5 Check the solutions obtained against the original equation 𝟐𝒙 𝟐 + 𝟖𝒙 − 𝟏𝟎 = 𝟎 For 𝑥 = 1: 2𝑥2 + 8𝑥 − 10 = 0 2 1 2 + 8 1 − 10 = 0 2 1 + 8 − 10 = 0 2 + 8 − 10 = 0 0 = 0 For 𝑥 = 5: 2𝑥2 + 8𝑥 − 10 = 0 2 −5 2 + 8 −5 − 10 = 0 2 25 − 40 − 10 = 0 50 − 40 − 10 = 0 0 = 0 Click to go back HOME Click to proceed
- 19. 𝑩𝒐𝒕𝒉 𝒗𝒂𝒍𝒖𝒆𝒔 𝒐𝒇𝒙 𝒔𝒂𝒕𝒊𝒔𝒇𝒚 𝒕𝒉𝒆 𝒈𝒊𝒗𝒆𝒏 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏. 𝑺𝒐 𝒕𝒉𝒆 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝟐𝒙 𝟐 + 𝟖𝒙 + 𝟏𝟎 = 𝟎 𝒊𝒔 𝒕𝒓𝒖𝒆 𝒘𝒉𝒆𝒏 𝒙 = 𝟏 𝒐𝒓 𝒘𝒉𝒆𝒏 𝒙 = −𝟓 Answer :𝒕𝒉𝒆 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝟐𝒙 𝟐 + 𝟖𝒙 + 𝟏𝟎 = 𝟎 has two solutions: x = 1 and x = -5 Click to go back HOME Click to proceed
- 20. Direction: Factor thefollowing and Select the correct answer. 𝑨. 𝒙 − 𝟖 𝟐 𝑩. 𝒙 + 𝟒 𝟐 𝑪. 𝒙 + 𝟖 𝟐 𝒙 𝟐 − 𝟏𝟔𝒙 + 𝟔𝟒 𝒙 𝟐 + 𝟏𝟐𝒙 + 𝟑𝟔 A. 𝒙 + 𝟒 𝟐 𝑩. 𝒙 + 𝟏𝟐 𝟐 C. 𝒙 + 𝟔 𝟐 Click to go back HOME Click to proceed
- 21. 𝑨. 𝟐 +𝒙 𝟐 𝑩. 𝟏 + 𝒙 𝟐 𝑪. 𝟏 − 𝒙 𝟐 A. 𝟑𝒙 − 𝟏 𝟐 𝑩. 𝟑𝒙 + 𝟏 𝟐 C. 𝟗𝒙 + 𝟏 𝟐 𝑨. 𝟏 − 𝟏𝟐𝒙 𝟐 𝑩. 𝟏 + 𝟑𝟔𝒙 𝟐 𝑪. 𝟏 − 𝟔𝒙 𝟐 𝑨. 𝟑𝒙 + 𝟖 𝟐 𝑩. 𝟗𝒙 + 𝟖 𝟐 𝑪. 𝟑𝒙 − 𝟖 𝟐 𝟏 + 𝟐𝒙 + 𝒙 𝟐 𝟏 − 𝟏𝟐𝒙 + 𝟑𝟔𝒙 𝟐 𝟗𝒙 𝟐 − 𝟒𝟖𝒙 + 𝟔𝟒 𝟗𝒙 𝟐 − 𝟔𝒙 + 𝟏 Click to go back HOME Click to proceed
- 22. Direction: Solve thefollowing Quadratic equation by completing the square 𝒙 𝟐 + 𝟕𝒙 + 𝟏𝟐 = 𝟎 𝒙 𝟐 + 𝟔𝒙 + 𝟓 = 𝟎 𝒙 𝟐 + 𝟖𝒙 + 𝟏𝟓 = 𝟎 𝟒𝒙 𝟐 − 𝟑𝟐𝒙 = −𝟐𝟖 Click to go back HOME Click to proceed
- 23. 1. 𝒙 𝟐 +𝟕𝒙 + 𝟏𝟐 = 𝟎 2. 𝒙 𝟐 + 𝟔𝒙 + 𝟓 = 𝟎 𝒙 𝟐 + 𝟕𝒙 = −𝟏𝟐 𝒙 𝟐 + 𝟕𝒙 + 𝟒𝟗 𝟒 = −𝟏𝟐 + 𝟒𝟗 𝟒 𝒙 + 𝟕 𝟐 𝟐 = 𝟏 𝟒 𝒙 + 𝟕 𝟐 = ± 𝟏 𝟒 𝒙 + 𝟕 𝟐 = ± 𝟏 𝟐 𝒙 + 𝟕 𝟐 = 𝟏 𝟐 𝒙 = 𝟏 𝟐 − 𝟕 𝟐 𝒙 = −𝟑 𝒙 + 𝟕 𝟐 = − 𝟏 𝟐 𝒙 = − 𝟏 𝟐 − 𝟕 𝟐 𝒙 = −𝟒 Therefore, the solutions are -3 and -4 𝒙 𝟐 + 𝟔𝒙 = −𝟓 𝒙 𝟐 + 𝟔𝒙 + 𝟗 = −𝟓 + 𝟗 𝒙 + 𝟑 𝟐 = ± 𝟒 𝒙 + 𝟑 = ±𝟐 𝒙 + 𝟑 = 𝟐 𝒙 = 𝟐 − 𝟑 𝒙 = −𝟏 𝒙 + 𝟑 = −𝟐 𝒙 = −𝟐 − 𝟑 𝒙 = −𝟓 Therefore, the solutions are -1 and -5 Click for 3 and 4 solution Click to go back HOME
- 24. 3. 𝒙 𝟐 +𝟖𝒙 + 𝟏𝟓 = 𝟎 4. 𝟒𝒙 𝟐 − 𝟑𝟐𝒙 = −𝟐𝟖 𝒙 𝟐 + 𝟖𝒙 = −𝟏𝟓 𝒙 𝟐 + 𝟖𝒙 + 𝟏𝟔 = −𝟏𝟓 + 𝟏𝟔 𝒙 + 𝟒 𝟐 = 𝟏 𝒙 + 𝟒 = ± 𝟏 𝒙 + 𝟒 = ±𝟏 Therefore, the solutions are -3 and -5 Therefore, the solutions are 7 and 1 𝒙 + 𝟒 = 𝟏 𝒙 = 𝟏 − 𝟒 𝒙 = −𝟑 𝒙 + 𝟒 = −𝟏 𝒙 = −𝟏 − 𝟒 𝒙 = −𝟓 𝟒𝒙 𝟐 − 𝟑𝟐𝒙 = −𝟐𝟖 𝟒 𝒙 𝟐 − 𝟖𝒙 = −𝟕 𝒙 𝟐 − 𝟖𝒙 + 𝟏𝟔 = −𝟕 + 𝟏𝟔 𝒙 − 𝟒 𝟐 = 𝟗 𝒙 − 𝟒 = ± 𝟗 𝒙 − 𝟒 = ±𝟑 𝒙 − 𝟒 = 𝟑 𝒙 = 𝟑 + 𝟒 𝒙 = 𝟕 𝒙 − 𝟒 = −𝟑 𝒙 = −𝟑 + 𝟒 𝒙 = 𝟏 Click to go back HOME
- 25. Click to goback HOME Click to proceed
- 26. Use the figureas a guide. Let x be the length of a side of the square piece of metal. The box will have a height of 1 foot and its square base will have x-2 as the length of a side. The volume of the box is therefore Length x width x height = 𝟏 𝒙 − 𝟐 𝒙 − 𝟐 = 𝒙 − 𝟐 𝟐 Since the volume of the box is to be 4 cubic feet, 𝒙 − 𝟐 𝟐 = 𝟒 𝒙 − 𝟐 = ±𝟐 𝒙 − 𝟐 = −𝟐 𝒙 = 𝟎 𝒙 − 𝟐 = 𝟐 𝒙 = 𝟒 or1 1 x x-2 Discard the solution 𝒙 = 𝟎 because length cannot be zero. Therefore, the sheet metal should be 4 feet by 4 feet Click to go back HOME
- 27. Answer key Activity 1.Quadratic or Not Activity 2: Am I a Perfect Square Trinomial or Not? Activity 3. Transform Me! 1. 𝒙 − 𝟐 𝟐 2. 𝒚 − 𝟔 𝟐 3. 𝒛 − 𝟓 𝟐 4. ( 𝒘 + Assessment Card 1 Assessment Card 2 Click to go back HOME
- 28. Click to goback HOME
- 29. Click to goback HOME
- 30.
- 31.
- 32.
- 33. Click to goback HOME
- 34. Click to goback HOME
- 35. Click to goback HOME
- 36.
- 37.
- 38.
- 39. HOME Click to goback &
- 40. HOME Reference Card Learner’s Material-MathematicsIX, First Edition pp. 35-45. Alferez, Duro et al. MSA ADVANCED ALGEBRA. MSA Publishing House. Quezon city, Philppines, 2012 pp. 58-63. http://www.themathpage.com/alg/perfect-square-trinomial.htm http://mathbitsnotebook.com/Algebra1/Factoring/FCPerfSqTri.html http://www.onemathematicalcat.org/algebra_book/online_problems/word_problems_ perfect_squares.htm