The document presents a detailed overview of time series forecasting techniques, focusing on various methods such as exponential smoothing, state space models, and recurrent neural networks (RNNs). It discusses key concepts like the decomposition of time series, the Buys-Ballot model, and the optimization of parameters through techniques like cross-validation. Additionally, it emphasizes the relevance of machine learning approaches for analyzing time series data and includes practical applications using R programming.


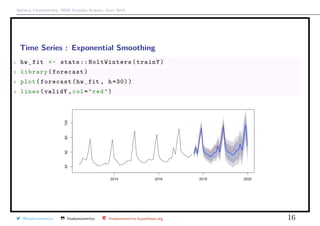
![Arthur Charpentier, SIDE Summer School, July 2019
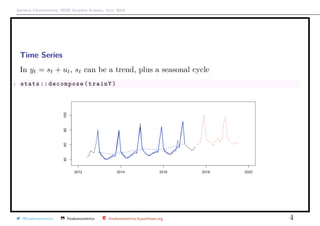
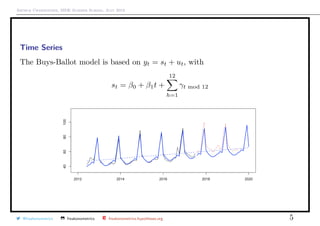
Time Series
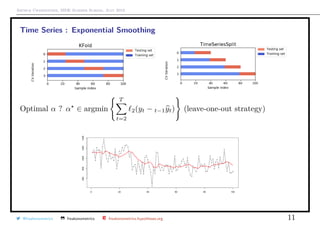
Consider the general prediction tyt+h = m(information available at time t)
1 hp <- read.csv("http:// freakonometrics .free.fr/ multiTimeline .csv",
skip =2)
2 T=86 -24
3 trainY <- ts(hp[1:T,2], frequency= 12, start= c(2012 , 6))
4 validY <- ts(hp[(T+1):nrow(hp) ,2], frequency= 12, start= c(2017 , 8))
@freakonometrics freakonometrics freakonometrics.hypotheses.org 3](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-3-320.jpg)




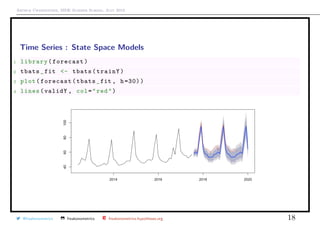
![Arthur Charpentier, SIDE Summer School, July 2019
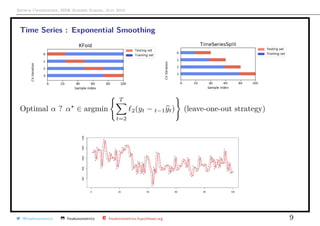
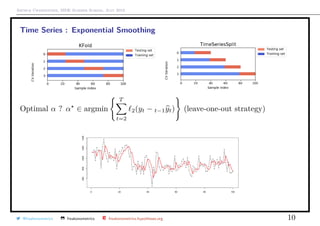
Time Series : State Space Models
See De Livera, Hyndman & Snyder (2011, Forecasting Time Series With Complex
Seasonal Patterns Using Exponential Smoothing),based on Box-Cox transformation
on yt: y
(λ)
t =
yλ
t − 1
λ
if λ = 0 (otherwise log yt)
See forecast::tbats
1 library(forecast)
2 forecast :: tbats(trainY)$lambda
3 [1] 0.2775889
@freakonometrics freakonometrics freakonometrics.hypotheses.org 17](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-17-320.jpg)


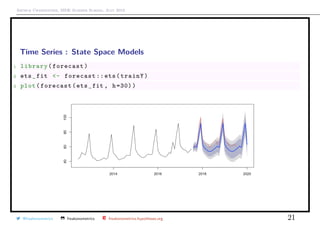
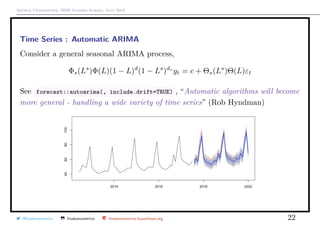

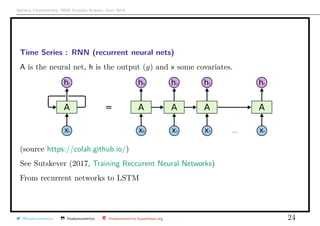
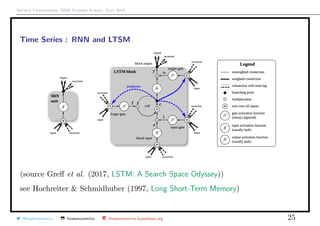
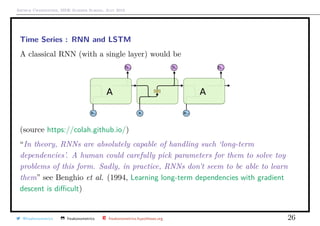

![Arthur Charpentier, SIDE Summer School, July 2019
Time Series : LSTM
C is the long-term state
H is the short-term state
forget gate: ft = sigmoid(Af [ht−1, xt] + bf )
input gate: it = sigmoid(Ai[ht−1, xt] + bi)
new memory cell: ˜ct = tanh(Ac[ht−1, xt] + bc)
@freakonometrics freakonometrics freakonometrics.hypotheses.org 28](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-28-320.jpg)
![Arthur Charpentier, SIDE Summer School, July 2019
Time Series : LSTM
final memory cell: ct = ft · ct−1 + it · ˜ct
output gate: ot = sigmoid(Ao[ht−1, xt] + bo)
ht = ot · tanh(ct)
@freakonometrics freakonometrics freakonometrics.hypotheses.org 29](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-29-320.jpg)
![Arthur Charpentier, SIDE Summer School, July 2019
Elicitable Measures & Forecasting
“elicitable” means “being a minimizer of a suitable expected score”, see Gneiting
(2011) Making and evaluating point forecasts.
Elicitable function
T is an elicatable function if there exits a scoring function S : R×R → [0, ∞)
T(Y ) = argmin
x∈R R
S(x, y)dF(y) = argmin
x∈R
E S(x, Y ) where Y ∼ F
Example: mean, T(Y ) = E[Y ] is elicited by S(x, y) = x − y 2
2
Example: median, T(Y ) = median[Y ] is elicited by S(x, y) = x − y 1
Example: quantile, T(Y ) = QY (τ) is elicited by
S(x, y) = τ(y − x)+ + (1 − τ)(y − x)−
Example: expectile, T(Y ) = EY (τ) is elicited by
S(x, y) = τ(y − x)2
+ + (1 − τ)(y − x)2
−
@freakonometrics freakonometrics freakonometrics.hypotheses.org 30](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-30-320.jpg)


![Arthur Charpentier, SIDE Summer School, July 2019
Probabilistic Forecasts
Notion of probabilistic forecasts, Gneiting & Raftery (2007 Strictly Proper Scoring
Rules, Prediction, and Estimation).
In a general setting, we want to predict value taken by random variable Y .
Let F denote a cumulative distribution function.
Let A denote the information available when forecast is made.
F is the ideal forecast for Y given A if the law of Y |A has distribution F.
Suppose F continuous. Set ZF = F(Y ), the probability integral transform of Y .
F is probabilistically calibrated if ZF ∼ U([0, 1])
F is marginally calibrated if E[F(y)] = P[Y ≤ y] for any y ∈ R.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 33](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-33-320.jpg)
![Arthur Charpentier, SIDE Summer School, July 2019
Probabilistic Forecasts
Observe that for a ideal forecast, F(y) = P[Y ≤ y|A], then
• E[F(y)] = E[P[Y ≤ y|A]] = P[Y ≤ y]
This forecast is est marginally calibrated
• P[ZF ≤ z] = E[P[ZF ≤ z|A]] = z
This forecast is probabilistically calibrated
Suppose µ ∼ N(0, 1). And that ideal forecast is Y |µ ∼ N(µ, 1).
E.g. if Yt ∼ N(0, 1) and Yt+1 = yt + εt ∼ N(yt, 1).
One can consider F = N(0, 2) as na¨ıve forecast. This distribution is marginally
calibrated, probabilistically calibrated and ideal.
One can consider F a mixture N(µ, 2) and N(µ ± 1, 2) where ”±1” means +1 or
−1 probability 1/2, hesitating forecast. This distribution is probabilistically
calibrated, but not marginally calibrated.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 34](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-34-320.jpg)
![Arthur Charpentier, SIDE Summer School, July 2019
Probabilistic Forecasts
Indeed P[F(Y ) ≤ u] = u,
P[F(Y ) ≤ u] =
P[Φ(Y ) ≤ u] + P[Φ(Y + 1) ≤ u]
2
+
P[Φ(Y ) ≤ u] + P[Φ(Y − 1) ≤ u]
2
One can consider F = N(−µ, 1). This distribution is marginally calibrated, but
not probabilistically calibrated.
In practice, we have a sequence (Yt, Ft) of pairs, (Y , F ).
The set of forecasts F is said to be performant if for all t, predictive distributions
Ft are precise (sharpness) and well-calibrated.
Precision is related to the concentration of the predictive density around a
central value (uncertainty degree).
Calibration is related to the coherence between predictive distribution Ft and
observations yt.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 35](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-35-320.jpg)

![Arthur Charpentier, SIDE Summer School, July 2019
Probabilistic Forecasts
One can also consider a score S(F, y) for all distribution F and all observation y.
The score is said to be proper if
∀F, G, E[S(G, Y )] ≤ E[S(F, Y )] where Y ∼ G.
In practice, this expected value is approximated using
1
n
n
t=1
S(Ft, Yt)
One classical rule is the logarithmic score S(F, y) = − log[F (y)] if F is (abs.)
continuous.
Another classical rule is the continuous ranked probability score (CRPS, see
Hersbach (2000, Decomposition of the Continuous Ranked Probability Score for
Ensemble Prediction Systems))
S(F, y) =
+∞
−∞
(F(x) − 1x≥y)2
dx =
y
−∞
F(x)2
+
+∞
y
(F(x) − 1)2
dx
@freakonometrics freakonometrics freakonometrics.hypotheses.org 37](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-37-320.jpg)
![Arthur Charpentier, SIDE Summer School, July 2019
Probabilistic Forecasts
with empirical version
S =
1
n
n
t=1
S(Ft, yt) =
1
n
n
t=1
+∞
−∞
(Ft(x) − 1x≥yt
)2
dx
studied in Murphy (1970, The ranked probability score and the probability score: a
comparison).
This rule is proper since
E[S(F, Y )] =
∞
−∞
E F(x) − 1x≥Y
2
dx
=
∞
−∞
[F(x) − G(x)]2
+ G(x)[1 − G(x)]
2
dx
is minimal when F = G.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 38](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-38-320.jpg)




![Arthur Charpentier, SIDE Summer School, July 2019
Natural Language Processing & Probabilistic Language Models
Idea : P[today is Wednesday] > P[today Wednesday is]
Idea : P[today is Wednesday] > P[today is Wendy]
E.g. try to predict the missing word I grew up in France, I speak fluent
@freakonometrics freakonometrics freakonometrics.hypotheses.org 43](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-43-320.jpg)
![Arthur Charpentier, SIDE Summer School, July 2019
Natural Language Processing & Probabilistic Language Models
Use of the chain rule
P[A1, A2, · · · , An] =
n
i=1
P[Ai|A1, A2, · · · , Ai−1]
P(the wine is so good)
= P(the) · P(wine|the) · P(is|the wine) · P(so|the wine is) · P(good|the wine is so)
Markov assumption & k-gram model
P[A1, A2, · · · , An] ∼
n
i=1
P[Ai|Ai−k, · · · , Ai−1]
@freakonometrics freakonometrics freakonometrics.hypotheses.org 44](https://image.slidesharecdn.com/sidearthur2019preliminary10-190719162744/85/Side-2019-10-44-320.jpg)