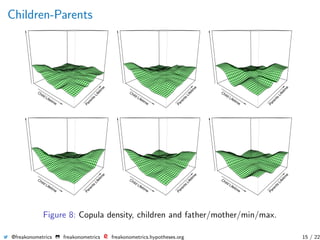
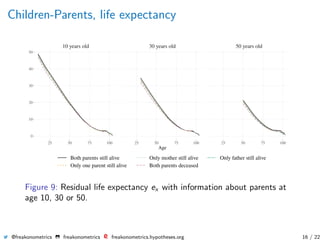
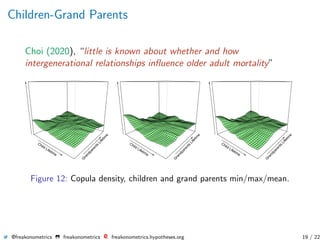
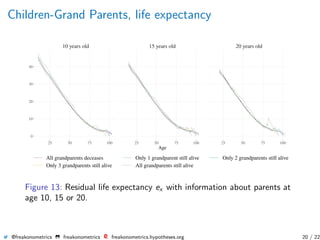
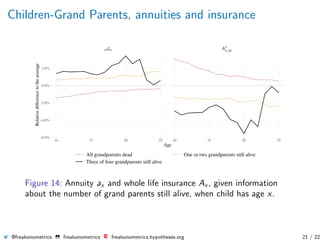
The document summarizes research on using genealogical data to model dependencies in life spans between family members and quantify the impact on insurance premiums. It presents analysis of husband-wife, parent-child, and grandparent-grandchild relationships, showing dependencies exist. Mortality rates, life expectancies, and insurance quantities like annuities are estimated conditionally based on family history information.

1. Family History and Life Insurance
Arthur Charpentier, Ewen Gallic & Olivier Cabrignac
UQAM, AMSE & SCOR, 2020
Online International Conference
in Actuarial science, data science and finance
@freakonometrics freakonometrics freakonometrics.hypotheses.org 1 / 22

2. Agenda
Motivations
Genealogical Data
‘Family History’ & Life Insurance
Husband-Wife
Children-Parents
Grand Children-Grand Parents
Using genealogical trees to understand dependencies in life spans
and quantify the impact on (life related) insurance premiums
@freakonometrics freakonometrics freakonometrics.hypotheses.org 2 / 22

3. ‘Family History’ & Insurance Forms
@freakonometrics freakonometrics freakonometrics.hypotheses.org 3 / 22

4. Genealogical Data
Charpentier and Gallic (2020a) comparing our collaborative based
dataset (238,009 users, 1,547,086 individual born in [1800, 1805)),
with official historical data
Charpentier and Gallic (2020b) on generational migration
@freakonometrics freakonometrics freakonometrics.hypotheses.org 4 / 22

5. Genealogical Data & “Generations”
Initial starting generation (born in [1800, 1805))
then children (born ∼ [1815, 1870)), grand children (born
∼ [1830, 1915)), grand grand children (born ∼ [1850, 1940))
0
5
10
1800 1820 1840 1860 1880 1900 1920 1940
Year of birth
Numberofindividuals(log)
1800-1804 Generation Children Grandchildren Great-grandchildren
@freakonometrics freakonometrics freakonometrics.hypotheses.org 5 / 22

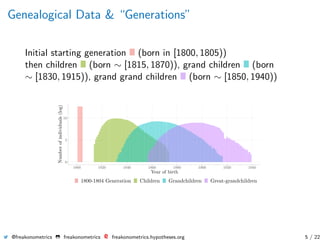
6. Demographic & Insurance Notations
tpx = P[T(x) > t] = P[T−x > t|T > x] =
P[T > t + x]
P[T > x]
=
S(x + t)
S(x)
.
curtate life expectancy for Tx is defined as
ex = E Tx = E T − x |T > x =
∞
t=0
ttpx · qx+t =
∞
t=1
tpx ,
actuarial present value of the annuity of an individual age (x) is
ax =
∞
k=1
νk
kpx or ax:n =
n
k=1
νk
kpx ,
and whole life insurance (see Bowers et al. (1997))
Ax =
∞
k=1
νk
kpx · qx+k or A1
x:n =
n
k=1
νk
kpx · qx+k.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 6 / 22

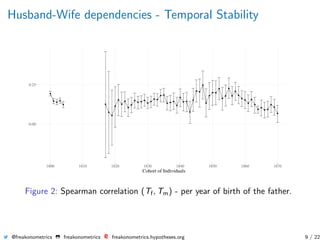
7. Historical Mortality
Survival Probability Logarithms of probabilities of dying
0 10 20 30 40 50 60 70 80 90 100 110 10 20 30 40 50 60 70 80 90 100 110
0.001
0.01
0.1
1
0.00
0.25
0.50
0.75
1.00
age
Women Men
Geneanet Generation mortality tables from Vallin and Mesl´e (2001)
Figure 1: Survival distribution tp0 = P[T > t] and force of mortality
1qx = P[T ≤ x + 1|T > x] (log scale), against historical data.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 7 / 22

8. Husband-Wife dependencies
birth (bf) death (df) age (tf) birth (bm) death (dm) age (tm)
i bf,i df,i tf,i bm,i dm,i tm,i
1 1800-05-04 1835-02-22 34.80356 1762-07-01 1838-01-19 75.55099
2 1778-02-09 1841-02-02 62.97878 1758-07-05 1825-08-03 67.07734
3 1771-01-18 1807-01-17 35.99452 1752-12-28 1815-10-31 62.83641
4 1768-07-01 1814-10-15 46.28611 1768-07-01 1830-12-06 62.42847
5 1766-07-01 1848-01-12 81.53046 1767-02-10 1851-04-22 84.19165
6 1769-06-28 1836-08-28 67.16496 1773-12-17 1825-02-15 51.16222
Table 1: Dataset for the joint life model, father/husband (f) and
mother/spouse (m)
@freakonometrics freakonometrics freakonometrics.hypotheses.org 8 / 22

9. Husband-Wife dependencies - Temporal Stability
0.00
0.25
1800 1810 1820 1830 1840 1850 1860 1870
Cohort of Individuals
Figure 2: Spearman correlation (Tf, Tm) - per year of birth of the father.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 9 / 22

10. Husband-Wife dependencies
Father Lifetime
M
otherLifetim
e
Figure 3: Nonparametric estimation of the copula density, (Tf, Tm).
see Frees et al. (1996), Carriere (1997), or Denuit et al. (2001)
Here ρS = 0.168, 95% confidence interval (0.166; 0, 171)
@freakonometrics freakonometrics freakonometrics.hypotheses.org 10 / 22

11. Husband-Wife dependencies
Father residual lifetim
e
M
otherresiduallifetim
e
Father residual lifetim
e
M
otherresiduallifetim
e
Father residual lifetim
e
M
otherresiduallifetim
e
Father residual lifetim
e
M
otherresiduallifetim
e
Father residual lifetim
e
M
otherresiduallifetim
e
Father residual lifetim
e
M
otherresiduallifetim
e
Figure 4: Copula density of remaining life times (Tf, Tm) given Tf ≥ x
(father on top, mother below).
@freakonometrics freakonometrics freakonometrics.hypotheses.org 11 / 22

12. Husband-Wife dependencies
Multiple life quantities, e.g. widow’s pension,
am|f =
∞
k=1
νk
kpxf
−
∞
k=1
νk
kpxf,xm , where tpxf,xm = P Txf
> t, Txm > t,
-8.0%
-6.0%
-4.0%
-2.0%
20 30 40 50 60 70
Age at time of subscription
Relativecostofwidow’spension
Figure 5: Widow’s pension, am|f (relative to independent case a⊥
m|f).
@freakonometrics freakonometrics freakonometrics.hypotheses.org 12 / 22

13. Children-Parents
“inheritance of longevity”
coined in Pearl (1931)
“the life spans of parents and chil-
dren appear only weakly related, even
though parents affect their children’s
longevity through both genetic and
environmental influences”
Vaupel (1988)
“the chance of reaching a high age is
transmitted from parents to children
in a modest, but robust way”
V˚ager¨o et al. (2018)
Figure 6: Son vs. parents Beeton
and Pearson (1901).
@freakonometrics freakonometrics freakonometrics.hypotheses.org 13 / 22

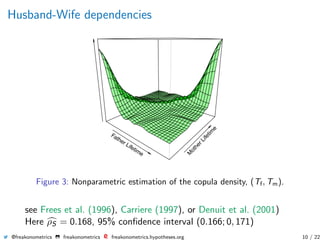
14. Children-Parents
Beeton and Pearson (1901), regression of Txc given Txf
or Txm
slope :
Daughter–mother
0.1968 [0.1910,0.20260]
Son–mother
0.1791 [0.1737,0.18443]
Daughter–father
0.1186 [0.1122,0.12507]
Son–father
0.1197 [0.1138,0.12567]
0
25
50
75
20 40 60 80 100
Age at death of mother
(a) Daughters on mothers
0
25
50
75
20 40 60 80 100
Age at death of mother
(b) Sons on mothers
0
25
50
75
20 40 60 80 100
Age at death of father
(c) Daughters on fathers
0
25
50
75
20 40 60 80 100
Age at death of father
(d) Sons on fathers
Conditional Means GAM Linear regression
Quantile Regression (τ = 0.1) Quantile Regression (τ = 0.9)
Figure 7: Age of the children given
information relative to the parents.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 14 / 22

15. Children-Parents
Child Lifetim
e
Parents
Lifetim
e
Child Lifetim
e
Parents
Lifetim
e
Child Lifetim
e
Parents
Lifetim
e
Child Lifetim
e
Parents
Lifetim
e
Child Lifetim
e
Parents
Lifetim
e
Child Lifetim
e
Parents
Lifetim
e
Figure 8: Copula density, children and father/mother/min/max.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 15 / 22

16. Children-Parents, life expectancy
10 years old 30 years old 50 years old
25 50 75 100 25 50 75 100 25 50 75 100
0
10
20
30
40
50
Age
Both parents still alive Only mother still alive Only father still alive
Only one parent still alive Both parents deceased
Figure 9: Residual life expectancy ex with information about parents at
age 10, 30 or 50.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 16 / 22

17. Children-Parents, annuities and insurance
nax A1
x:n
20 30 40 50 20 30 40 50
0.4
0.5
16
18
20
22
Age
Both parents deceased Only one parent still alive Both parents still alive Reference
Figure 10: Annuity ax and whole life insurance Ax , given information
about the number of parents still alive, when child has age x.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 17 / 22

18. Children-Parents, annuities and insurance
nax A1
x:n
20 30 40 50 20 30 40 50
-4.0%
0.0%
4.0%
8.0%
Age
Relativedifferencetotheaverage
Both parents deceased Only one parent still alive Both parents still alive
Figure 11: Annuity ax and whole life insurance Ax , given information
about the number of parents still alive, when child has age x (relative
difference).
@freakonometrics freakonometrics freakonometrics.hypotheses.org 18 / 22

19. Children-Grand Parents
Choi (2020), “little is known about whether and how
intergenerational relationships influence older adult mortality”
Child Lifetim
e
G
randparents
Lifetim
e
Child Lifetim
e
G
randparents
Lifetim
e
Child Lifetim
e
G
randparents
Lifetim
e
Figure 12: Copula density, children and grand parents min/max/mean.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 19 / 22

20. Children-Grand Parents, life expectancy
10 years old 15 years old 20 years old
25 50 75 100 25 50 75 100 25 50 75 100
0
10
20
30
40
Age
All grandparents deceases Only 1 grandparent still alive Only 2 grandparents still alive
Only 3 grandparents still alive All grandparents still alive
Figure 13: Residual life expectancy ex with information about parents at
age 10, 15 or 20.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 20 / 22

21. Children-Grand Parents, annuities and insurance
nax A1
x:n
10 15 20 25 10 15 20 25
-6.0%
-4.0%
-2.0%
0.0%
2.0%
Age
Relativedifferencetotheaverage
All grandparents dead One or two grandparents still alive
Three of four grandparents still alive
Figure 14: Annuity ax and whole life insurance Ax , given information
about the number of grand parents still alive, when child has age x.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 21 / 22

22. References
Beeton, M. and Pearson, K. (1901). On the inheritance of the duration of life, and on
the intensity of natural selection in man. Biometrika, 1(1):50–89.
Bowers, N. L., Gerber, H. U., Hickman, J. C., Jones, D. A., and Nesbitt, C. J. (1997).
Actuarial Mathematics. Society of Actuaries, Shaumburg, IL, second edition.
Carriere, J. (1997). Bivariate survival models for coupled lives. Scandinavian Actuarial
Journal, pages 17–32.
Charpentier, A. and Gallic, E. (2020a). La d´emographie historique peut-elle tirer profit
des donn´ees collaboratives des sites de g´en´ealogie ? Population, to appear.
Charpentier, A. and Gallic, E. (2020b). Using collaborative genealogy data to study
migration: a research note. The History of the Family, 25(1):1–21.
Choi, S.-W. E. (2020). Grandparenting and mortality: How does race-ethnicity
matter? Journal of Health and Social Behavior.
Denuit, M., Dhaene, J., Le Bailly De Tilleghem, C., and Teghem, S. (2001).
Measuring the impact of a dependence among insured life lengths. Belgian
Actuarial Bulletin, 1(1):18–39.
Frees, E. W., Carriere, J., and Valdez, E. (1996). Annuity valuation with dependent
mortality. The Journal of Risk and Insurance, 63(2):229–261.
Pearl, R. (1931). Studies on human longevity. iv. the inheritance of longevity.
preliminary report. Human Biology, 3(2):245. Derni`ere mise `a jour - 2013-02-24.
Vaupel, J. W. (1988). Inherited frailty and longevity. Demography, 25(2):277–287.
V˚ager¨o, D., Aronsson, V., and Modin, B. (2018). Why is parental lifespan linked to
children’s chances of reaching a high age? a transgenerational hypothesis. SSM -
Population Health, 4:45 – 54.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 22 / 22