1) Support vector machines (SVMs) aim to find the optimal separating hyperplane that maximizes the margin between two classes of data points.
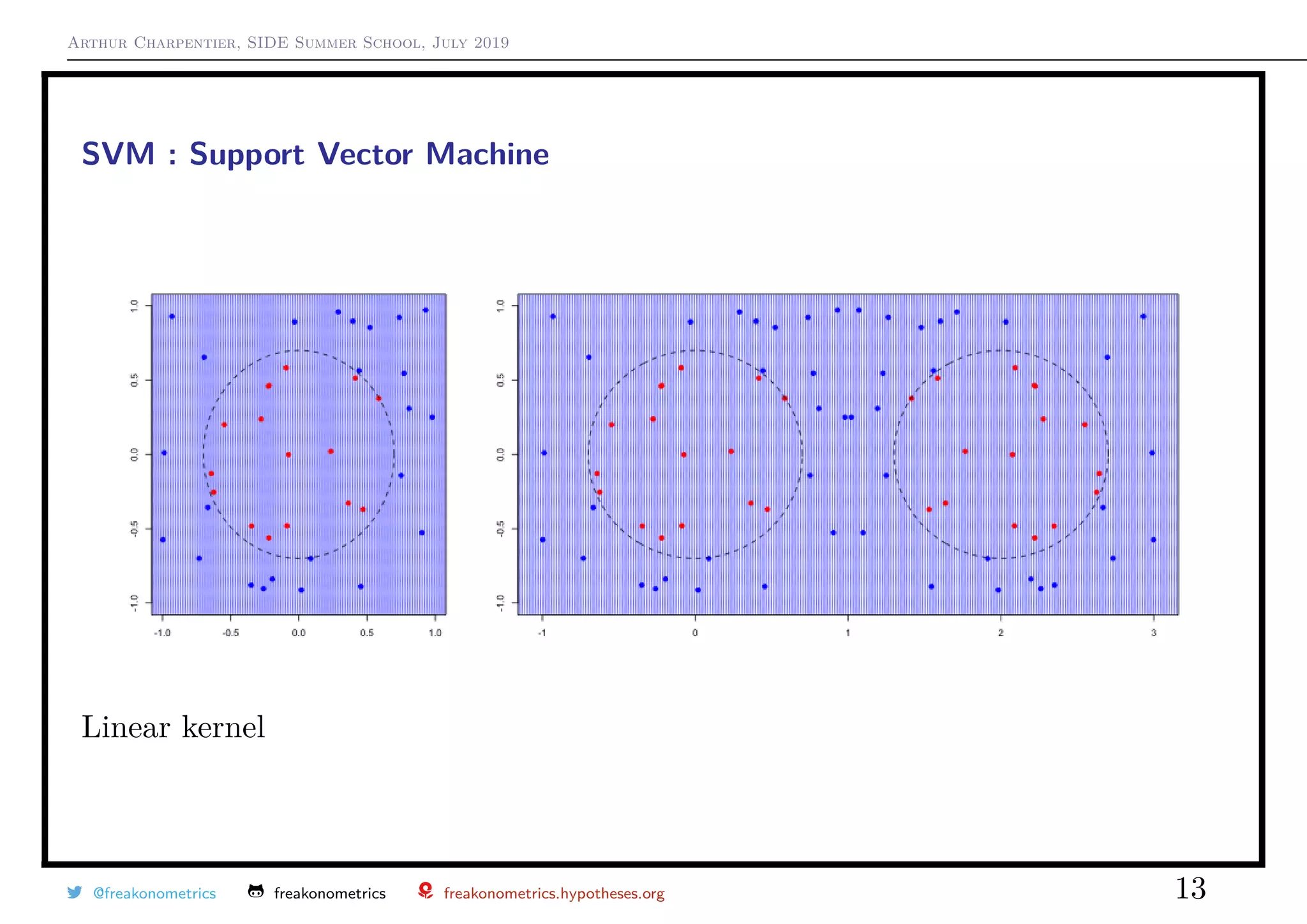
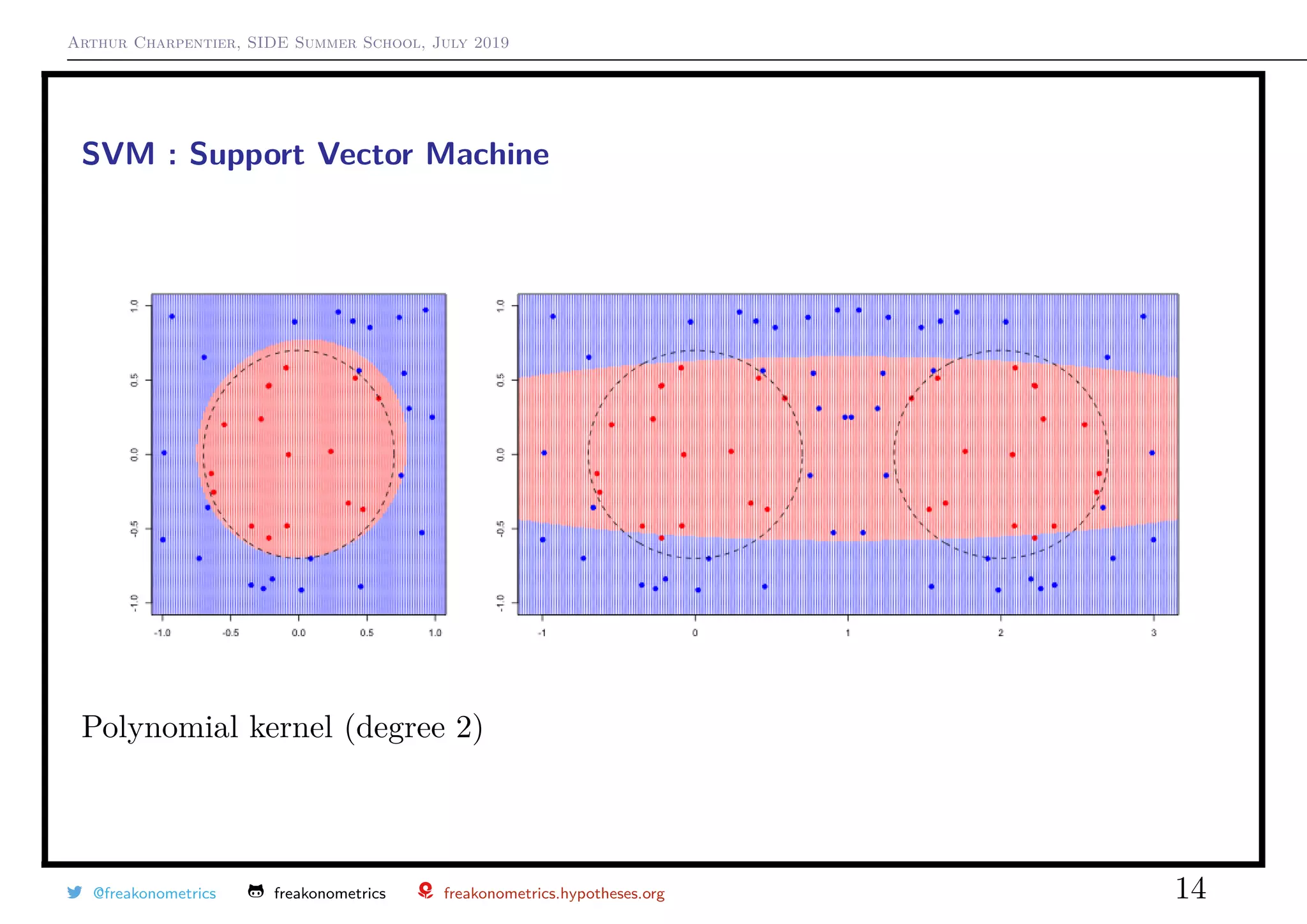
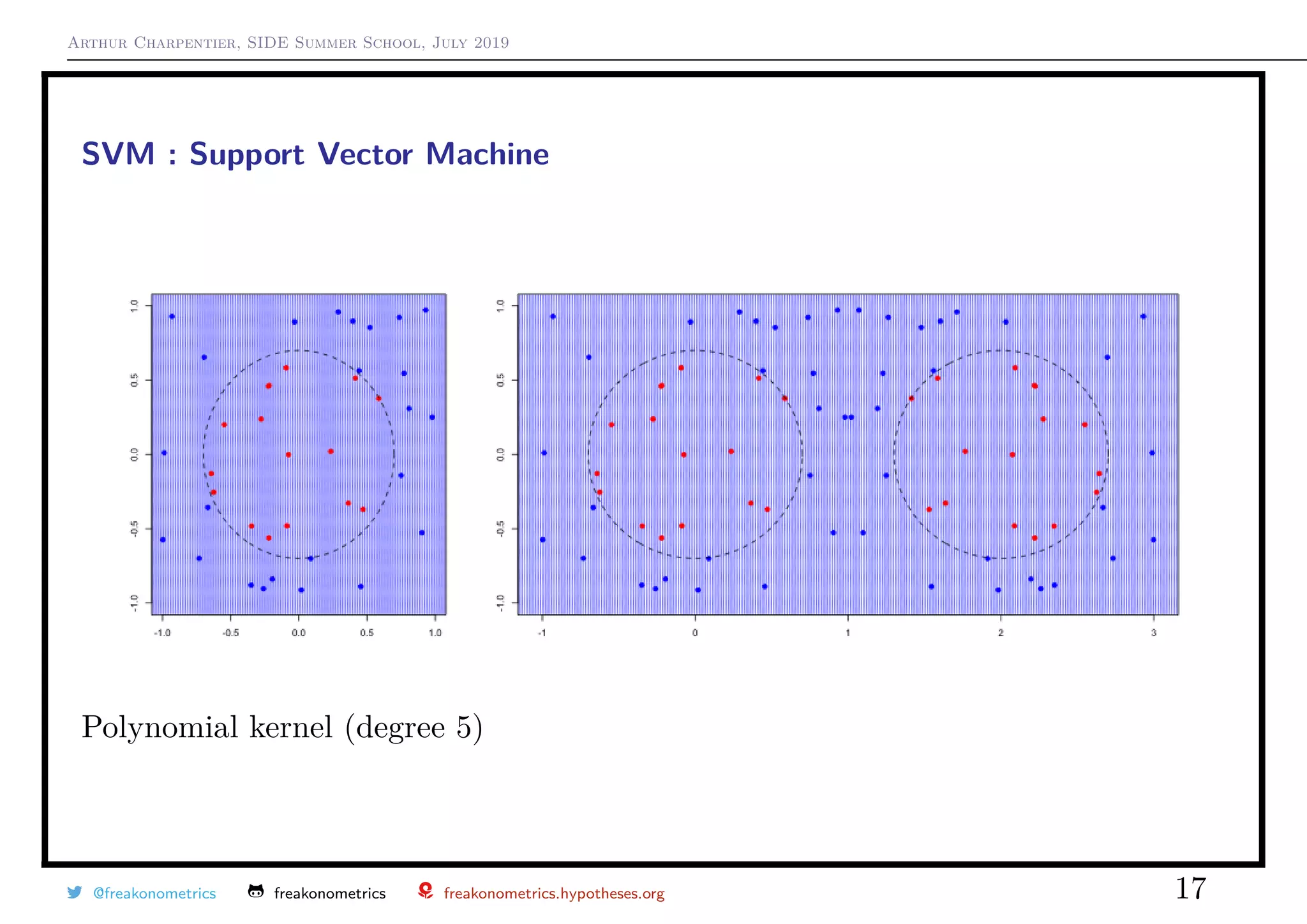
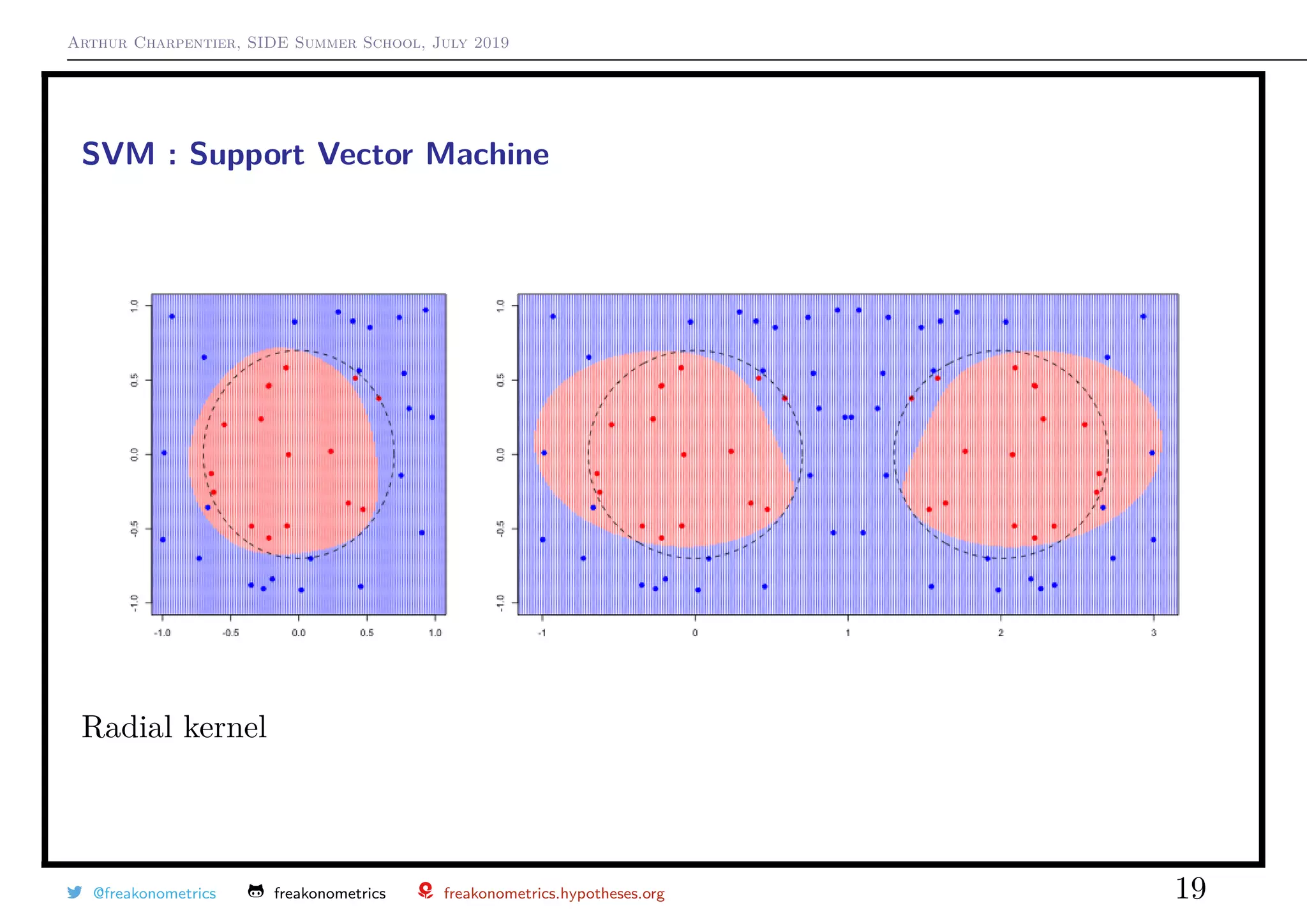
2) SVMs can be extended to non-linearly separable data using kernels to project the data into a higher dimensional feature space. Common kernels include polynomial and Gaussian radial basis function kernels.
3) The dual formulation of SVMs involves solving a quadratic programming problem to determine the support vectors, which lie closest to the separating hyperplane. These support vectors are then used to define the optimal hyperplane.

![Arthur Charpentier, SIDE Summer School, July 2019
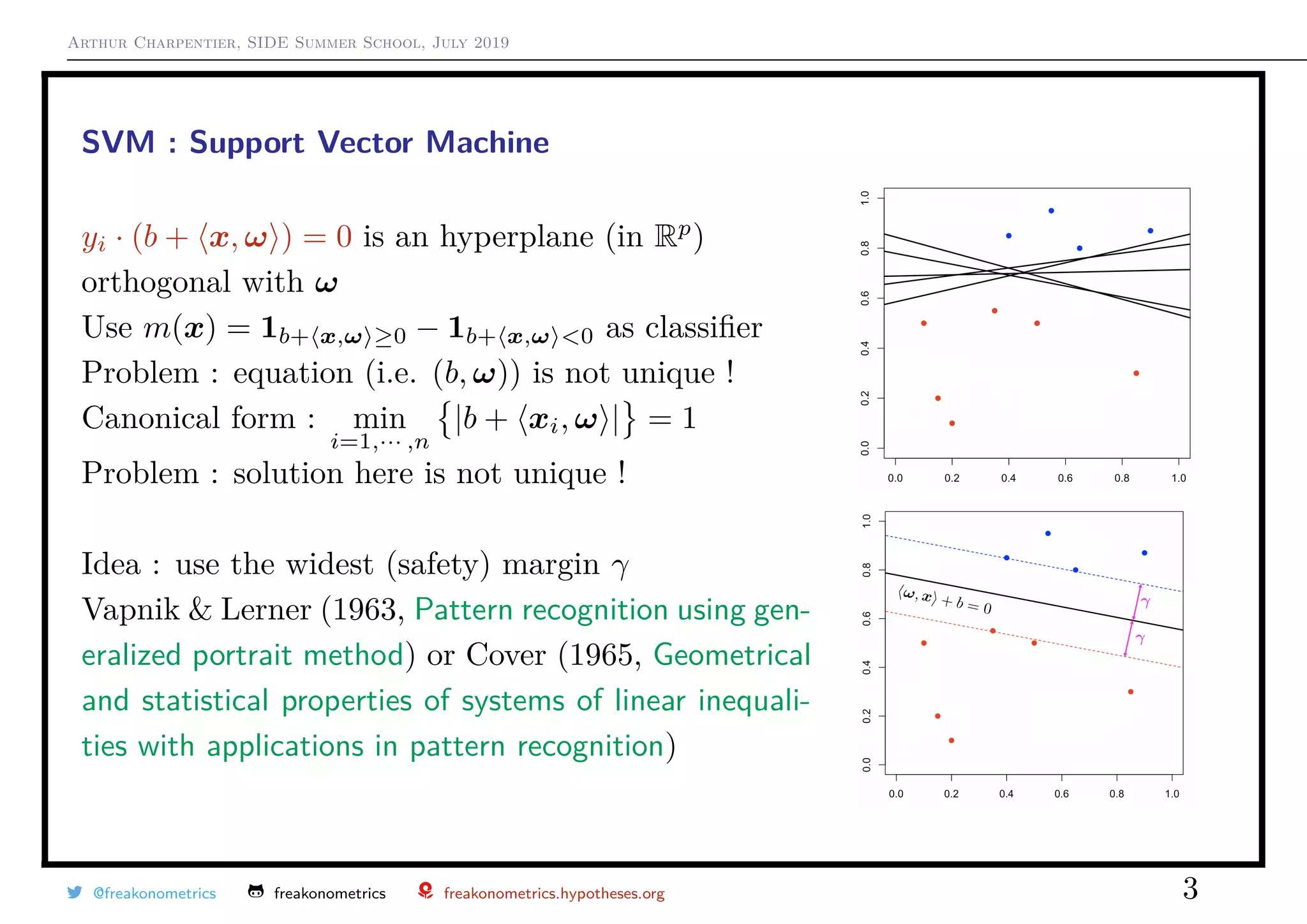
SVM : Support Vector Machine
Linearly Separable sample [econometric notations]
Data (y1, x1), · · · , (yn, xn) - with y ∈ {0, 1} - are
linearly separable if there are (β0, β) such that
- yi = 1 if β0 + x β > 0
- yi = 0 if β0 + x β < 0
Linearly Separable sample [ML notations]
Data (y1, x1), · · · , (yn, xn) - with y ∈ {−1, +1} - are
linearly separable if there are (b, ω) such that
- yi = +1 if b + x, ω > 0
- yi = −1 if b + x, ω < 0
or equivalently yi · (b + x, ω ) > 0, ∀i.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 2](https://image.slidesharecdn.com/sidearthur2019preliminary06-190716095506/75/Side-2019-6-2-2048.jpg)


![Arthur Charpentier, SIDE Summer School, July 2019
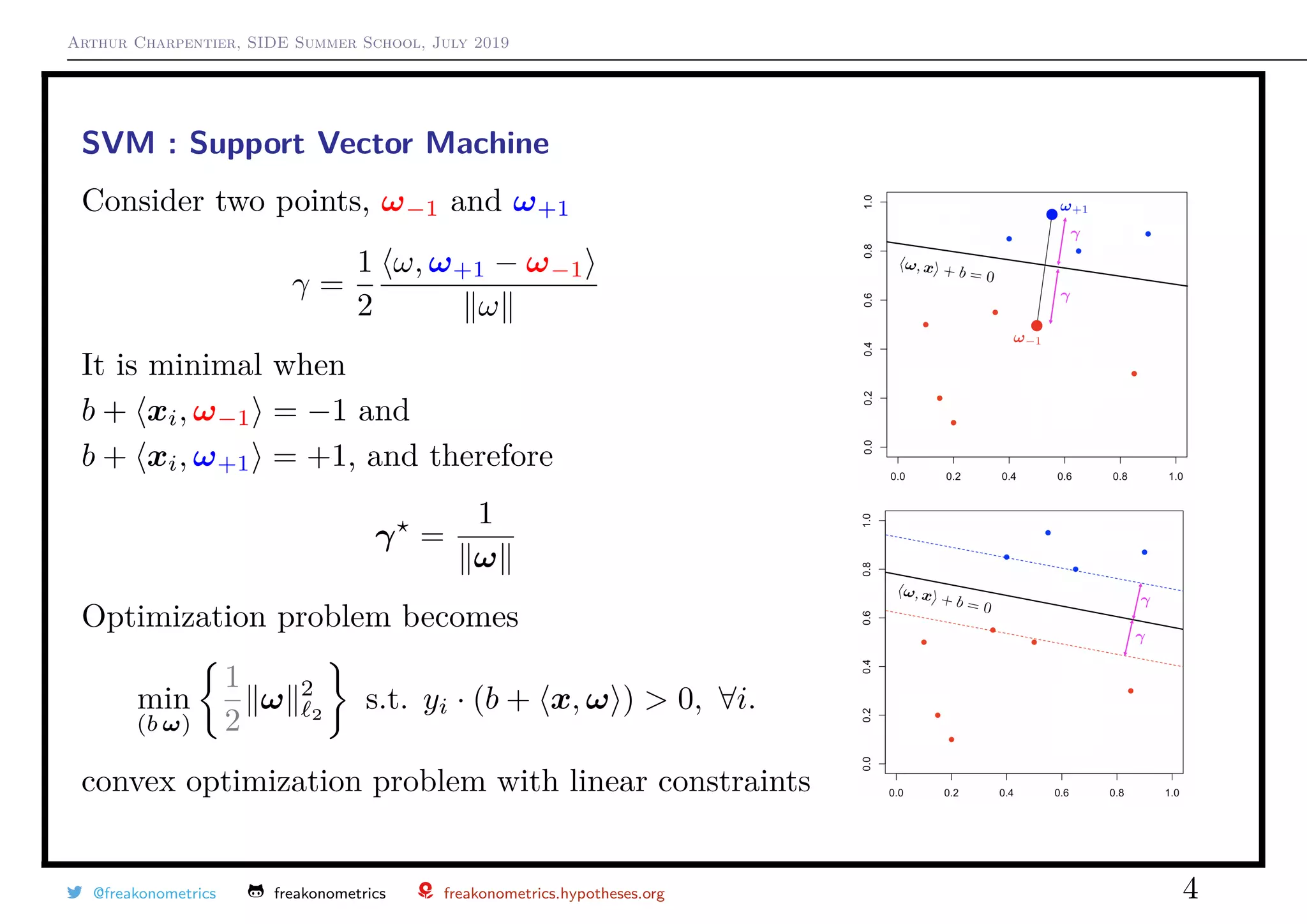
SVM : Support Vector Machine
min
α
1
2
α Qα − 1 α s.t.
αi ≥ 0, ∀i
y 1 = 0
where Q = [Qi,j] and Qi,j = yiyj xi, xj , and then
ω =
n
i=1
αi yixi and b = −
1
2
min
i:yi=+1
{ xi, ω } + min
i:yi=−1
{ xi, ω }
Points xi such that αi > 0 are called support
yi · (b + xi, ω ) = 1
Use m (x) = 1b + x,ω ≥0−1b + x,ω <0 as classifier
Observe that γ =
n
i=1
α 2
i
−1/2
@freakonometrics freakonometrics freakonometrics.hypotheses.org 7](https://image.slidesharecdn.com/sidearthur2019preliminary06-190716095506/75/Side-2019-6-7-2048.jpg)

![Arthur Charpentier, SIDE Summer School, July 2019
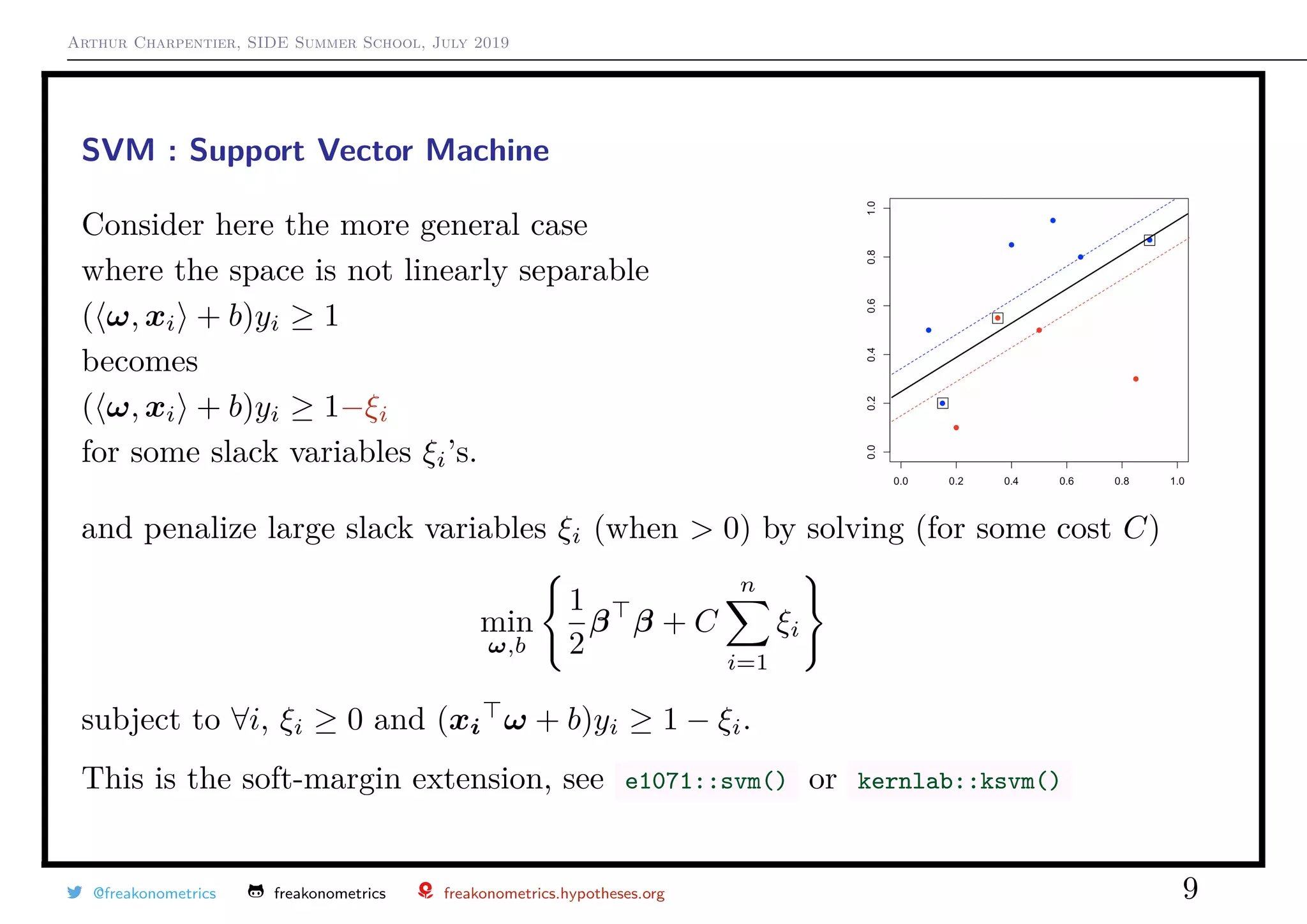
SVM : Support Vector Machine
The dual optimization problem is now
min
α
1
2
α Qα − 1 α s.t.
0 ≤ αi≤ C, ∀i
y 1 = 0
where Q = [Qi,j] and Qi,j = yiyj xi, xj , and then
ω =
n
i=1
αi yixi and b = −
1
2
min
i:yi=+1
{ xi, ω } + min
i:yi=−1
{ xi, ω }
Note further that the (primal) optimization problem can be written
min
(b,ω)
1
2
ω 2
2
+
n
i=1
1 − yi · (b + x, ω ) +
,
where (1 − z)+ is a convex upper bound for empirical error 1z≤0
@freakonometrics freakonometrics freakonometrics.hypotheses.org 10](https://image.slidesharecdn.com/sidearthur2019preliminary06-190716095506/75/Side-2019-6-10-2048.jpg)








![Arthur Charpentier, SIDE Summer School, July 2019
SVM : Support Vector Machine
A kernel is a measure of similarity between vectors.
The smaller the value of γ the narrower the vectors should be to have a small
measure
Is there a probabilistic interpretation ?
Platt (2000, Probabilities for SVM) suggested to use a logistic function over the
SVM scores,
p(x) =
exp[b + x, ω ]
1 + exp[b + x, ω ]
@freakonometrics freakonometrics freakonometrics.hypotheses.org 23](https://image.slidesharecdn.com/sidearthur2019preliminary06-190716095506/75/Side-2019-6-23-2048.jpg)