This document discusses classification and goodness of fit in machine learning. It introduces concepts like confusion matrices, ROC curves, and measures like sensitivity, specificity, and AUC. ROC curves are constructed by plotting the true positive rate vs. false positive rate for different classification thresholds. The AUC can measure classifier performance, with higher values indicating better classification. Chi-square tests and bootstrapping are also discussed for evaluating goodness of fit.

1. Arthur Charpentier, SIDE Summer School, July 2019
# 8 Classification & Goodness of Fit (Practical)
Arthur Charpentier (Universit´e du Qu´ebec `a Montr´eal)
Machine Learning & Econometrics
SIDE Summer School - July 2019
@freakonometrics freakonometrics freakonometrics.hypotheses.org 1

2. Arthur Charpentier, SIDE Summer School, July 2019
Test and Decision
truth
- +
-
true
negative
false
negative
decision
+
false
positive
true
positive
truth
- +
-
good
decision
type 2
error
decision
+
type 1
error
true
positive
We usually have a tradeoff between the two types of error, see base rate fallacy
In statistical terminology, we want to test an assumption (H0) - which can be
valid, or not - and we need to take a decision : reject H0 or accept H0.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 2

3. Arthur Charpentier, SIDE Summer School, July 2019
Test and Decision
Prevalence
200
10, 000
= 2%
Specificity
9, 751
9, 800
= 99.5%
Sensitivity
100
200
= 50%
Positive Predictive Value
100
149
∼ 67%
Specificity
9, 310
9, 800
= 95%
Positive Predictive Value
100
590
∼ 17%
- +
non-disease disease
- 9,751 100 9,851
decision
+ 49 100 149
9,800 200 10,000
non-disease disease
- 9,310 100 9,410
decision
+ 490 100 590
9,800 200 10,000
see Wainer & Savage (2008, Until proven guilty: False positives and war on terror).
@freakonometrics freakonometrics freakonometrics.hypotheses.org 3

4. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
Confusion matrix
Given a sample (yi, xi) and a model m, the confusion matrix is the contin-
gency table, with dimensions observed yi ∈ {0, 1} and predicted yi ∈ {0, 1}.
y
0(-) 1(+)
0(-) TN FN
y
1(+) FP TP
FP
TN+FP
TP
FN+TP
FPR TPR
Classical measures are
true positive rate (TPR) - or sensitivity
false positive rate (FPR) - or fall-out,
true negative rate (TNR) - or specificity
TNR = 1-FPR
among others (see wikipedia)
See ROCR::performance(prediction(Score,Y),"tpr","fpr")
@freakonometrics freakonometrics freakonometrics.hypotheses.org 4

5. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
ROC (Receiver Operating Characteristic) Curve
Assume that mt is define from a score function s, with mt(x) =
1(s(x) > t) for some threshold t. The ROC curve is the curve
(FPRt, TPRt) obtained from confusion matrices of mt’s.
n = 100 individuals
50 yi = 0 and 50 yi = 1
(well balanced)
@freakonometrics freakonometrics freakonometrics.hypotheses.org 5
q
q
Y=0 Y=1
OBSERVED
Y=1Y=0
PREDICTED
25 25
25 25
FPR TPR
25 25
50 50
~ 0.5 ~ 0.5
q
q
FALSE POSITIVE RATE
TRUEPOSITIVERATE
0.0 0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
q

6. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
29 deaths (y = 0) and 42 survivals (y = 1)
y =



1 if P[Y = 1|X] > 0%
0 if P[Y = 1|X] ≤ 0%
0%
y
0 1
0 0 0
y
1 29 42
29
29+0
42
42+0
= 100% = 100%
FPR TPR
@freakonometrics freakonometrics freakonometrics.hypotheses.org 6

7. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
29 deaths (y = 0) and 42 survivals (y = 1)
y =



1 if P[Y = 1|X] > 15%
0 if P[Y = 1|X] ≤ 15%
15%
y
0 1
0 17 2
y
1 12 40
12
17+12
40
42+2
∼ 41.4% ∼ 95.2%
FPR TPR
@freakonometrics freakonometrics freakonometrics.hypotheses.org 7

8. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
29 deaths (y = 0) and 42 survivals (y = 1)
y =



1 if P[Y = 1|X] > 50%
0 if P[Y = 1|X] ≤ 50%
50%
y
0 1
0 25 3
y
1 4 39
4
25+4
39
39+3
∼ 13.8% ∼ 92.8%
FPR TPR
@freakonometrics freakonometrics freakonometrics.hypotheses.org 8

9. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
29 deaths (y = 0) and 42 survivals (y = 1)
y =



1 if P[Y = 1|X] > 85%
0 if P[Y = 1|X] ≤ 85%
50%
y
0 1
0 28 13
y
1 1 29
1
28+1
29
29+13
∼ 3.4% ∼ 69.9%
FPR TPR
@freakonometrics freakonometrics freakonometrics.hypotheses.org 9

10. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
29 deaths (y = 0) and 42 survivals (y = 1)
y =



1 if P[Y = 1|X] > 100%
0 if P[Y = 1|X] ≤ 100%
50%
y
0 1
0 29 42
y
0 0 29
0
29+0
0
42+0
= 0.0% = 0.0%
FPR TPR
@freakonometrics freakonometrics freakonometrics.hypotheses.org 10

11. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
See Fawcett (2006, An introduction to ROC analysis)
AUC (Area Under the Curve) for classification
The AUC is the area enclosed by the ROC
curve
Gini’s γ for classification
γ = 2AUC − 1
AUC= γ = 1 for a perfect classifier
AUC= 1/2 and γ = 0 for a random classifier
see chi-square independence test
@freakonometrics freakonometrics freakonometrics.hypotheses.org 11

12. Arthur Charpentier, SIDE Summer School, July 2019
Chi-Square Test for Contingency Tables
brown hazel green blue
black 63.0% 13.9% 4.6% 18.5% 100.0%
brown 41.6% 18.9% 10.1% 29.4% 100.0%
red 36.6% 19.7% 19.7% 23.9% 100.0%
blond 5.5% 7.9% 12.6% 74.0% 100.0%
37.2% 15.7% 10.8% 36.3%
brown hazel green blue
black 30.9% 16.1% 7.8% 9.3% 18.2%
brown 54.1% 58.1% 45.3% 39.1% 48.3%
red 11.8% 15.1% 21.9% 7.9% 12.0%
blond 3.2% 10.8% 25.0% 43.7% 21.5%
100.0% 100.0% 100.0% 100.0%
@freakonometrics freakonometrics freakonometrics.hypotheses.org 12

13. Arthur Charpentier, SIDE Summer School, July 2019
Chi-Square Test for Contingency Tables
brown hazel green blue
black 68 15 5 20 108
brown 119 54 29 84 286
red 26 14 14 17 71
blond 7 10 16 94 127
220 93 64 215
brown hazel green blue
black 40 17 12 39 108
brown 106 45 31 104 286
red 26 11 8 26 71
blond 47 20 14 46 127
220 93 64 215
Compare ni,j and n⊥
i,j
n⊥
i,j =
ni,· × n·,j
n
@freakonometrics freakonometrics freakonometrics.hypotheses.org 13

14. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit
Be carefull of overfit...
Important to use
training / validation
• classification tree
• boosting classifier
@freakonometrics freakonometrics freakonometrics.hypotheses.org 14

15. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
ROC (Receiver Operating Characteristic ) Curve
Assume that mt is define from a score function s, with mt(x) =
1(s(x) > t) for some threshold t. The ROC curve is the curve
(FPRt, TPRt obtained from confusion matrices of mt’s.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 15
qq qqq qq
q
qq qqqq qqqq
q
qqqqq
q
qqq qqq qq
qq
qqqqqqqqqq qqq qq
q
qq qqq qqqq qq qq qq qqq
q
q qq qqq q qq qq q qqqqq qqq qqqq qqqq qq qqqq q
q
qqq qq qqq qqq qqq qq qqq qqqqqqq q qqqqq q qqq
q
qq qq qqq
q
q
q
qqq qq qqqq q qq q qqqq qqq q qq qqq qqq qq qqqq qqqq
q
q qqq qqqq
q
qq
q
q
qq
qq qqq q qqqq
q
qqq qqq qqqqqq qq q
q
qq qqq qqq q qqqqq qqq q
q
q qq qq qqqq
q
qqqq qqqqq q qqq qq
q
qqq q
q
q q qqq
q
qq qqq qqq qq qqq q
q
q qq qqq qq
q
q qqqq qq
q
q q
q
qq q
qq
qqq
q
q qqq q
q
qqqq qqqqq qqqq qqqq qqq
q
q qq qq qqqq q
q
qqq
q
qqq qqqq qq q qq q qq qqqqqq q qqqq q qqqq qqqqq
q
qq q qq qqqq qqqq
q
q
qq
qq q
q
qqq qqqq q
q
q
q
qq qq
qq
qqq q qq q qqqq qqqq qqqq qq qq qq qqqq qqqq q qqqq qqqq
q
q qqqq qqq qqq q
q
qq qqqq qqqqqqqq qq qqqq qqq q
q
qq qq
q
q q qqqq qqq q qqq q q qqqqqq q
q
q q qqqqq q q qqqq qqqq q qqqq qqqqq qq qqq q
q
qqq qq qqqq qq qq
qq
qqqqqq qq qqq
q
q qqqqqq
q
q qq qq q qqq q qqq q qq qq qqq q
q
qq q
q
q qq qq qq
q
q qqq qqq qqqqq qqqq q qqqqq
q
q
q
q q
qq
qq
q
qqqq
q
q qq q q
q
q
q
qqqq qq qq q qqq q qq qqqqqq qq qq qqqq qqqq q qqqq qq q qq qq qqqq q qq q
q
qqqqq qqqq qq qq qqqq q qqq
q
qq
q
qq qqqq qqqqq qqqq qq qqq qqq qqqq qq q q
q
qqq qq qq
q
qq qq qqq qq qqqqq qqq qqq qqqqq qqqqq qq qqq qqqq qqq q qq qq qqqq q qq qq qqqqq qq qqqq
qq
qqqqqqqq qqqq qq q
q
qqqqq qqq qq
q
qqqqq
q
q q
q
qqq qq q qqqq qq q qqqq qqqq qqqqq qq qqqqq
q
q q qq qqq qqq q
q
q
q
q qq q qqqq
q
qqq q qq qq q
SCORE S
OBSERVATIONY
0.0 0.2 0.4 0.6 0.8 1.0
Y=0
Y=1
FALSE POSITIVE RATE
TRUEPOSITIVERATE
0.0 0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
q

16. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit: ROC Curve
With categorical variables, we have a collection of points
Need to interpolate between those points to have a curve, see convexification of
ROC curves, e.g. Flach (2012, Machine Learning)
@freakonometrics freakonometrics freakonometrics.hypotheses.org 16
q
q
FALSE SPAM RATE
TRUESPAMRATE
0.0 0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
q
q
q
q
q
q
FALSE SPAM RATE
TRUESPAMRATE
0.0 0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
q
q

17. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit
One can derive a confidence interval of the ROC curve
using boostrap techniques,
pROC::ci.se()
Various measures can be used see library hmeasures ,
with Gini index, the Area Under the curve, or
Kolmogorov-Smirnov for classification
ks = sup
t∈R
|F1(t) − F0(t)|
ks = sup
t∈R



1
n1 i:yi=1
1s(xi)≤t −
1
n0 i:yi=0
1s(xi)≤t



Specificity (%)
Sensitivity(%)
020406080100
100 80 60 40 20 0
0.0 0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
Fn(x)
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
Survival
Death
@freakonometrics freakonometrics freakonometrics.hypotheses.org 17

18. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit
The Area Under the Curve, AUC, can be interpreted as the probability that a
classifier will rank a randomly chosen positive instance higher than a randomly
chosen negative one, see Swets, Dawes & Monahan (2000, Psychological Science
Can Improve Diagnostic Decisions)
Kappa statistic κ compares an Observed Accuracy with an Expected Accuracy
(random chance), see Landis & Koch (1977, The Measurement of Observer
Agreement for Categorical Data)
Y = 0 Y = 1
Y = 0 TN FN TN+FN
Y = 1 FP TP FP+TP
TN+FP FN+TP n
See also Obsersed and Random Confusion Tables
Y = 0 Y = 1
Y = 0 25 3 28
Y = 1 4 39 43
29 42 71
Y = 0 Y = 1
Y = 0 11.44 16.56 28
Y = 1 17.56 25.44 43
29 42 71
@freakonometrics freakonometrics freakonometrics.hypotheses.org 18

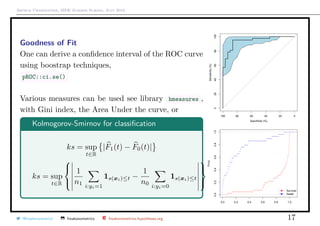
19. Arthur Charpentier, SIDE Summer School, July 2019
Goodness of Fit
Accuracy for classification
(total) accuracy =
TP + TN
n
total accuracy =
TP + TN
n
∼ 90.14%
random accuracy =
[TN + FP] · [TP + FN] + [TP + FP] · [TN + FN]
n2
∼ 51.93%
Cohen’s κ for classification
κ =
(total) accuracy − random accuracy
1 − random accuracy
from Cohen, Jacob (1960, A coefficient of agreement for nominal scales). Here
κ ∼ 79.48%.
@freakonometrics freakonometrics freakonometrics.hypotheses.org 19