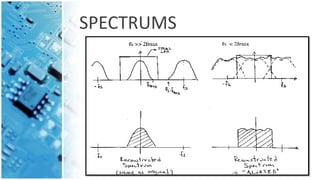
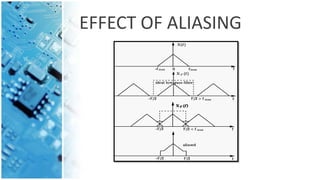
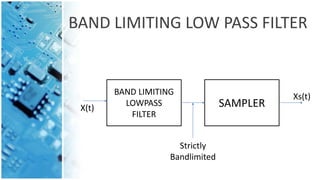
This document discusses the sampling theorem and its key aspects. It introduces the sampling theorem, which states that a signal can be reconstructed from its samples if it is sampled at least twice its maximum frequency. It then provides two statements that comprise the combined sampling theorem statement - that a signal containing frequencies up to W Hz can be determined from samples spaced 1/2W seconds apart, and recovered from those same samples. The document also mentions spectrums, aliasing effects, and using a low-pass filter to band-limit signals before sampling.

1. PREPARED BY
KETAN NAYAK (140413117005)
HARSH PARMAR(140413117006)
UNDER GUIDANCE OF
PROF. JANKI CHOTAI

2. INDEX
Sr. NO TOPIC
1. INTRODUCTION
2. STATEMENT
3. SPECTRUMS
4. EFFECT OF ALIASING
5. BAND LIMITING LOW PASS FILTER

3. INTRODUCTION
• Sampling Theorem was Introduced to
Communication Theory in 1949 by Shannon.
• The Sampling Theorem States that the Higher
Number of Samples the Closer its
Representation.
• No of Samples depend on Sampling Rate and
Maximum Frequency of the Signal to be
Sampled.

4. STATEMENT
1. If a Finite Energy Signal x(t) contains
Frequency Higher than “W” Hz then It is
Completely determined by Specifying its
Values at Instants of Time Which are Spaced
(½) Second Apart.
2. If a Finite Energy Signal x(t) contains No
Frequency components higher than W Hz then
it may be Completely Removed from its
Samples which are Spaced (½)w Second Apart.

5. COMBINED STATEMENT
• A Continuous Time Signal x(t) can be completely
represented in its sampled form and recovered
back from sampled form if the Sampling
Frequency Fs ≥ 2W where w is Maximum
Frequency of Continious Time Signal x(t).

6. SPECTRUMS

7. EFFECT OF ALIASING

8. BAND LIMITING LOW PASS FILTER
BAND LIMITING
LOWPASS
FILTER
SAMPLER
Xs(t)
X(t)
Strictly
Bandlimited