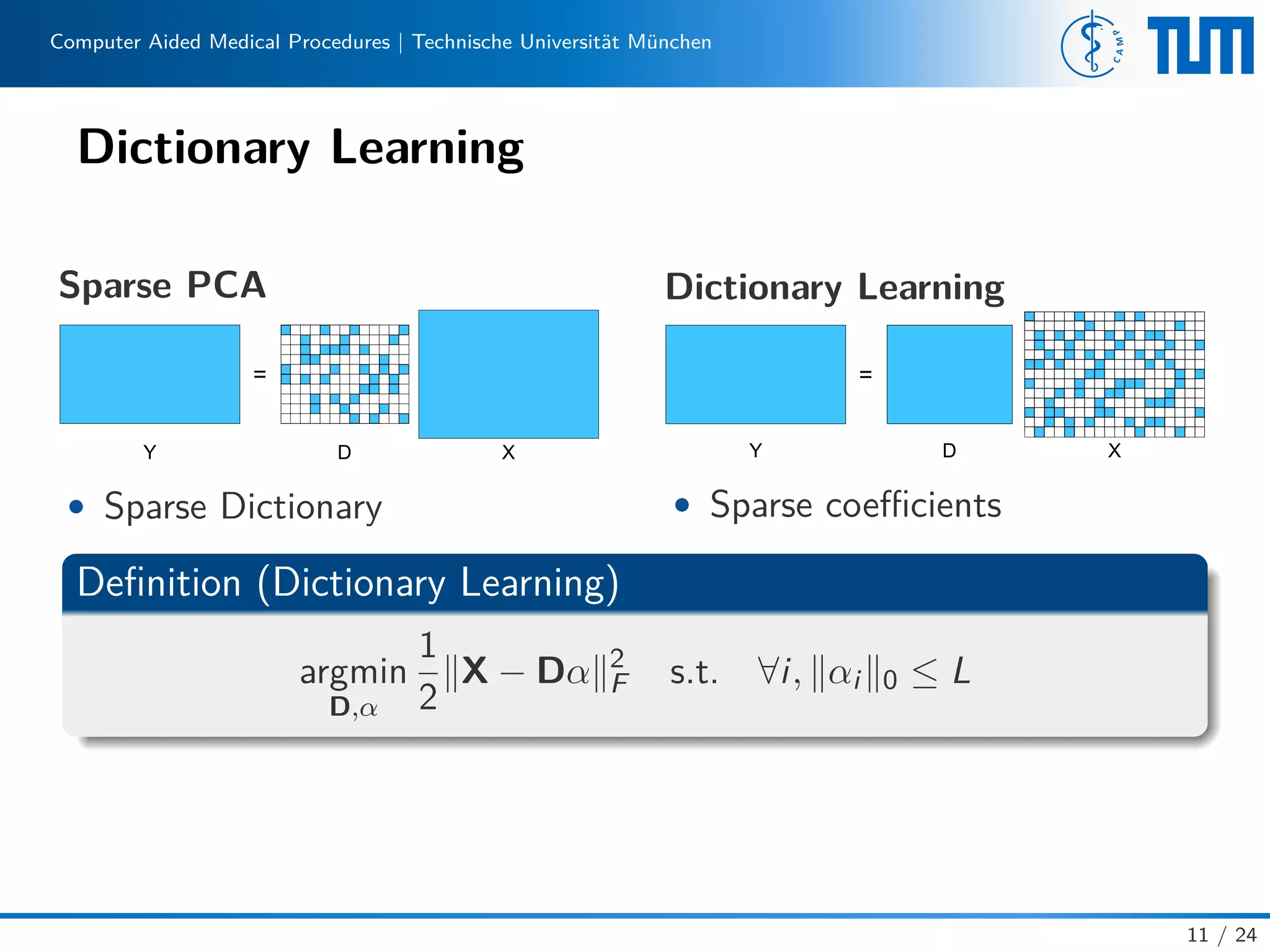
This document provides an introduction to sparse methods, including regularization techniques and compressive sensing. It discusses how regularization can address ill-posed problems by adding constraints that encourage simple or sparse solutions. Compressive sensing aims to reconstruct sparse signals from few measurements. Dictionary learning seeks an overcomplete basis to sparsely represent signals via linear combinations of atoms. Algorithms like orthogonal matching pursuit and K-SVD are described for solving dictionary learning problems. The document outlines extensions of these sparse methods.

1. Introduction to Sparse Methods
Shadi Albarqouni, M.Sc.
Research Assistant | PhD Candidate
shadi.albarqouni@tum.de
Computer Aided Medical Procedures | Technische Universität München
Machine Learning in Medical Imaging
BioMedical Computing (BMC) Master Program

2. Computer Aided Medical Procedures | Technische Universität München
Outline
1 Introduction
1. Ordinary Least Square
2. Posedness
2 Regularization
1. Tikhonov Regularization
2. L1 Regularization
3. Regularization-Extensions
3 Sparsity
1. Compressive Sensing
2. Dictionary Learning (Sebastian Pölsterl’s slides)
OMP
K-SVD
DL-Extensions
3. Sparse Graph
2 / 24

3. Computer Aided Medical Procedures | Technische Universität München
Notation
• y ∈ Rm is the observed signal/labels
• A ∈ Rm×n is some Blurring, Projection, or Fitting matrix
• x ∈ Rn is the latent signal/samples
• η ∈ Rn is the Gaussian noise
• Objective: Find solution x, such that minimizing the energy of
noise η
Definition (Least Square Error / Maximum Likelihood)
xLS/ML = argmin
x
1
2
y − Ax 2
2
3 / 24

4. Computer Aided Medical Procedures | Technische Universität München
Ordinary Least Square Error
Closed-form Solution
˜xLS/ML = (AT
A)−1
AT
y
What if:
• A is overdeter-
mined/underdetermined
matrix
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
−1
−0.5
0
0.5
1
0
0.5
1
1.5
2
2.5
3
3.5
4 / 24

5. Computer Aided Medical Procedures | Technische Universität München
Ordinary Least Square Error
Closed-form Solution
˜xLS/ML = (AT
A)−1
AT
y
What if:
• A is overdeter-
mined/underdetermined
matrix
• A is
ill-conditioned
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
−1
−0.5
0
0.5
1
0
0.5
1
1.5
2
2.5
3
3.5
4 / 24

6. Computer Aided Medical Procedures | Technische Universität München
Ordinary Least Square Error
Closed-form Solution
˜xLS/ML = (AT
A)−1
AT
y
What if:
• A is overdeter-
mined/underdetermined
matrix
• A is
ill-conditioned
• A is singular
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
−1
−0.5
0
0.5
1
0
0.5
1
1.5
2
2.5
3
3.5
4 / 24

7. Computer Aided Medical Procedures | Technische Universität München
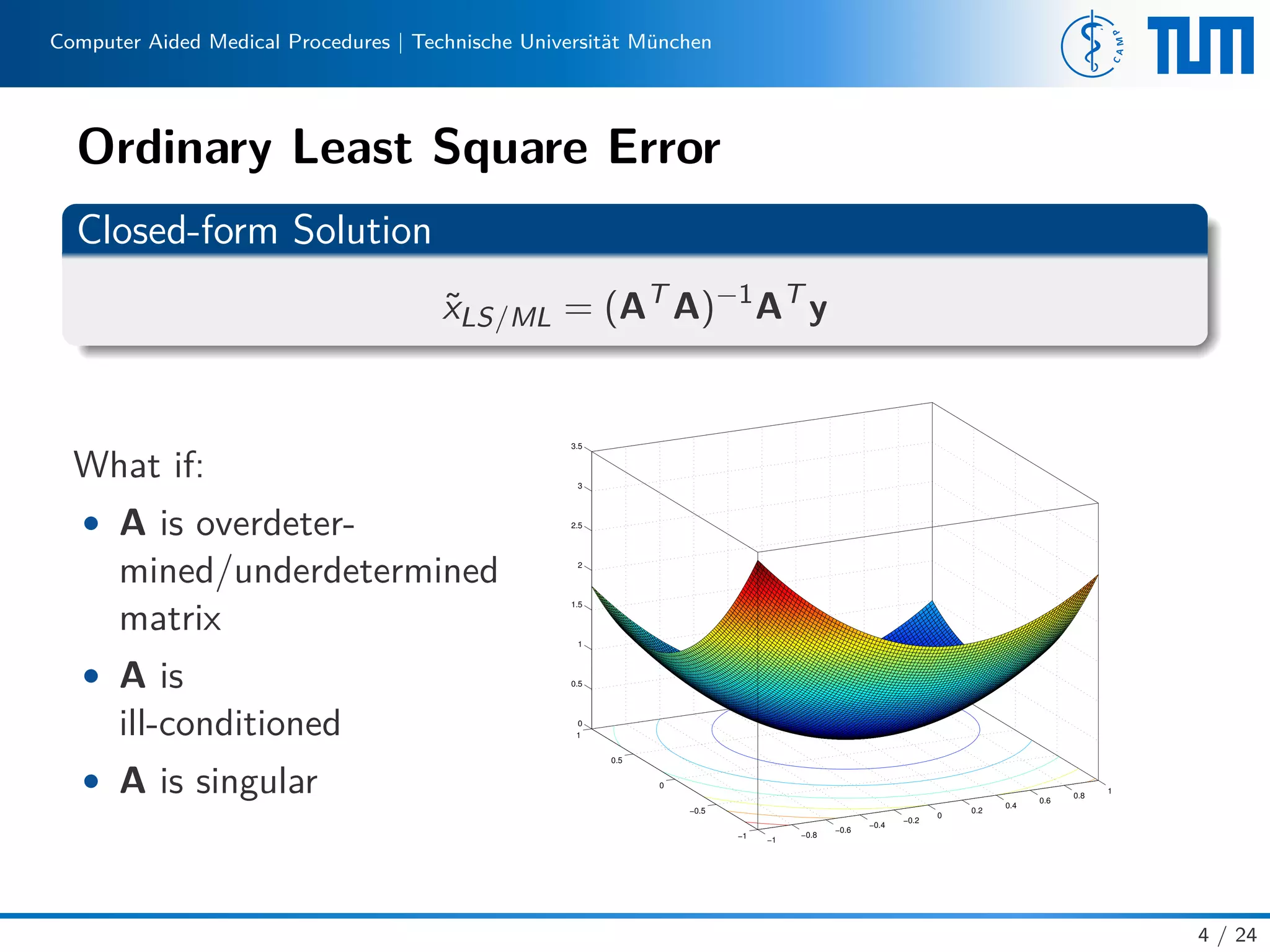
Posedness
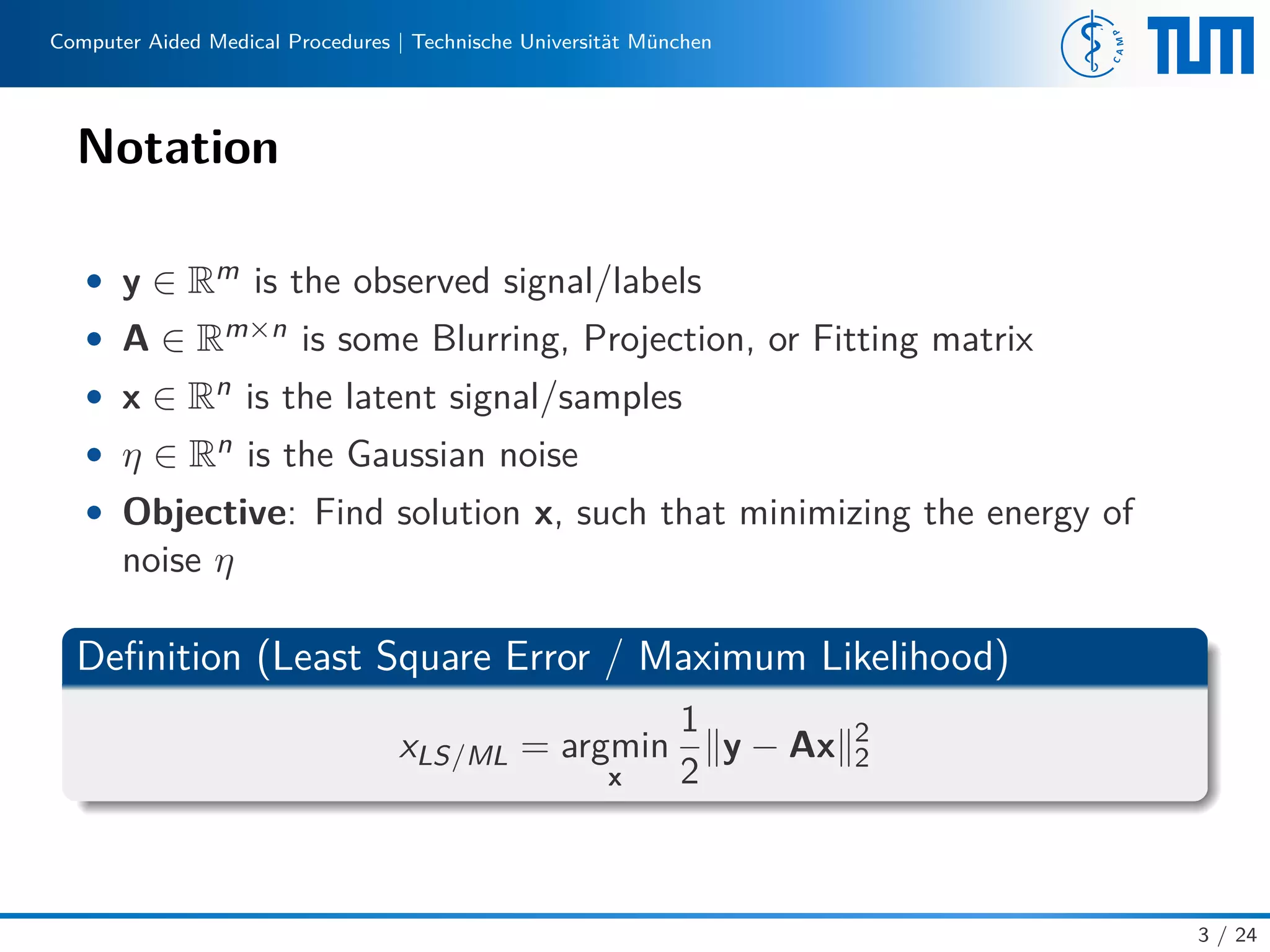
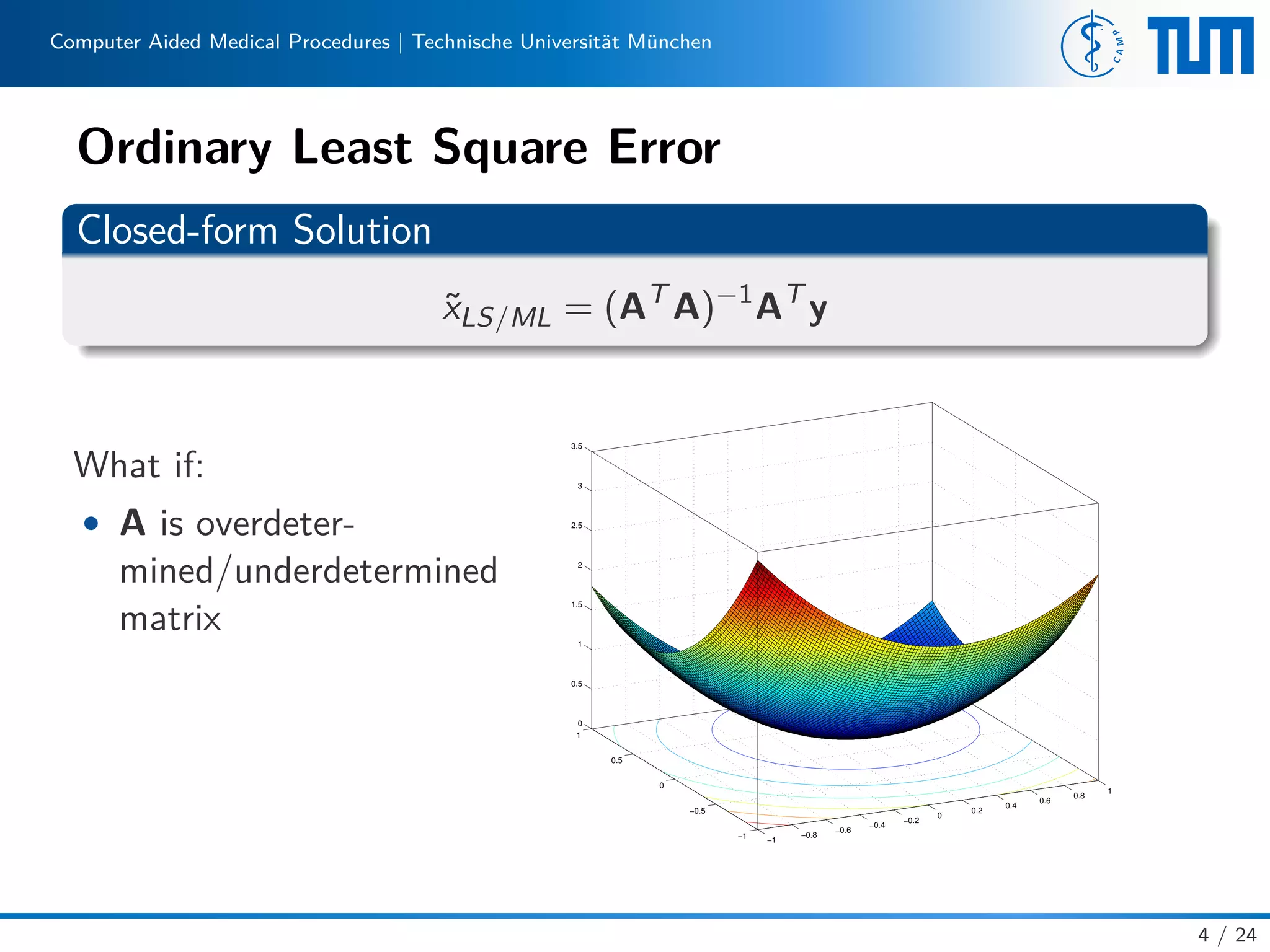
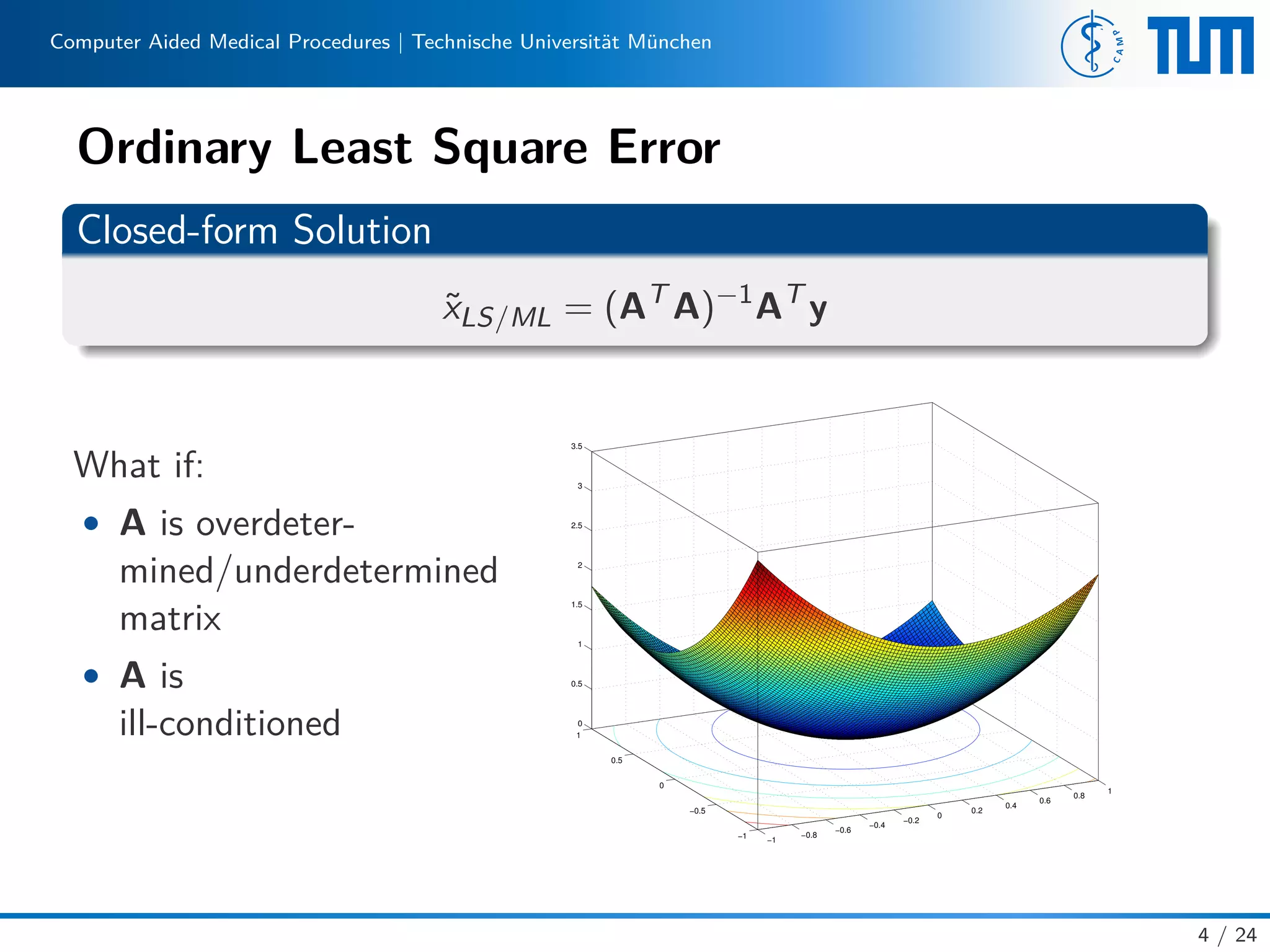
Definition (Well-Posed Problem)
According to Hadamard[1], a problem is well-posed if
1. It has a solution
2. The solution is unique
3. The solution depends continuously on data and parameters.
Define the following, and
explain their impacts:
• ill-posed problem
• well-conditioned
• ill-conditioned
−1
−0.5
0
0.5
1
−1
−0.5
0
0.5
1
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
5 / 24

8. Computer Aided Medical Procedures | Technische Universität München
Regularization
Definition (Tikhonov Regularization)
xL2 = argmin
x
1
2
y − Ax 2
2 +
λ
2
x 2
2
What happens when we increase x looking for the solution:
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
6 / 24

9. Computer Aided Medical Procedures | Technische Universität München
Regularization
Definition (L1 Regularization)
xL1 = argmin
x
1
2
y − Ax 2
2 +
λ
2
x 1
What happens when we increase x looking for the solution:
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
7 / 24

10. Computer Aided Medical Procedures | Technische Universität München
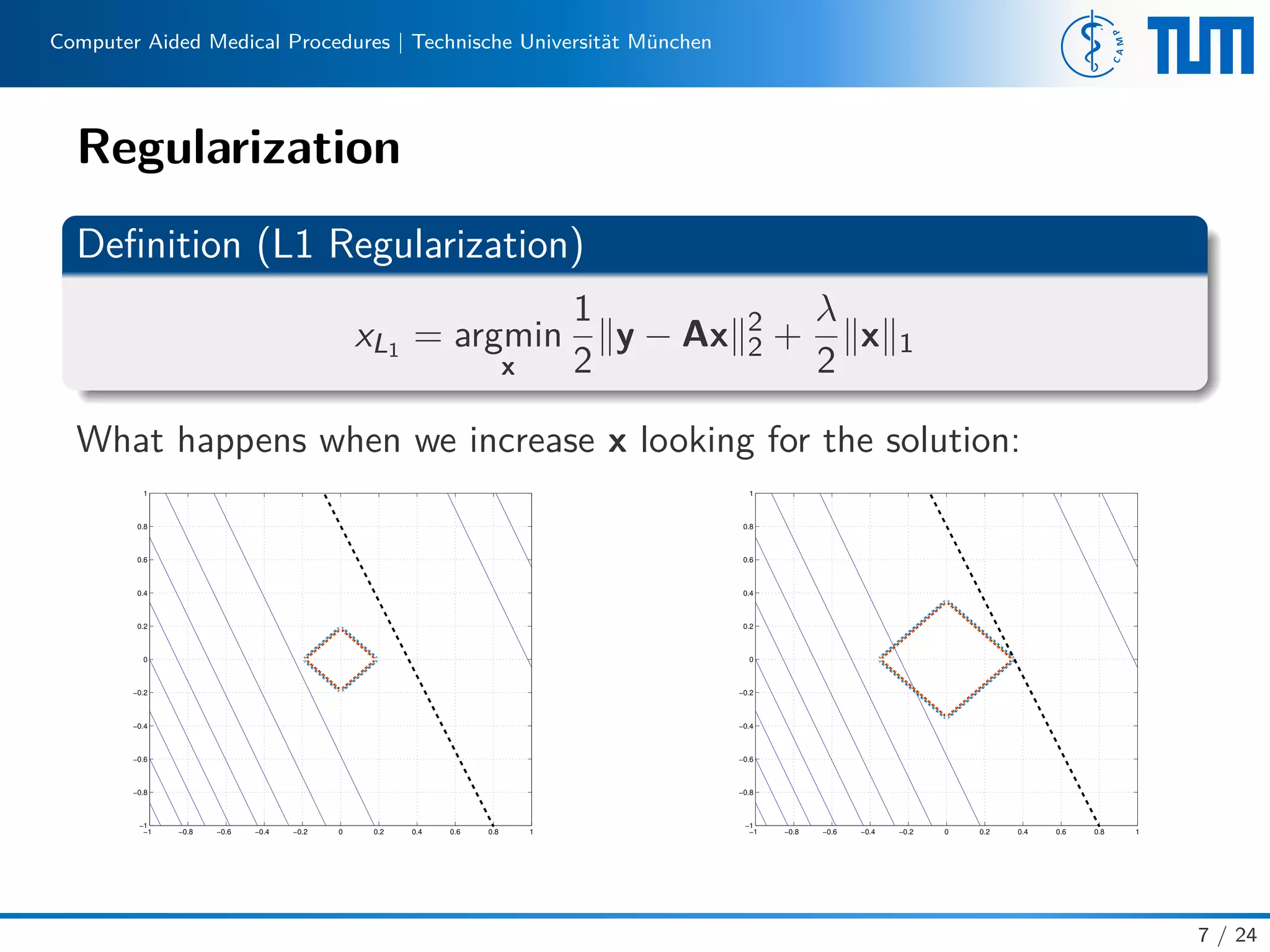
Regularization-Extensions
Definition (General Regularization)
xRLS/MAP = argmin
x
1
2
y − Ax 2
2 + λP(x)
• Incorporate different regularization terms into the objective
function p-norm x p [2] [3]
x 0 x 1 x 2 x 4
8 / 24

11. Computer Aided Medical Procedures | Technische Universität München
Regularization-Extensions
Definition (General Regularization)
xRLS/MAP = argmin
x
1
2
y − Ax 2
2 + λP(x)
• Incorporate different regularization terms into the objective
function p-norm x p [2] [3]
x 0 x 1 x 2 x 4
• Use other RKHS function
8 / 24

12. Computer Aided Medical Procedures | Technische Universität München
Regularization-Extensions
Definition (General Regularization)
xRLS/MAP = argmin
x
1
2
y − Ax 2
2 + λP(x)
• Incorporate different regularization terms into the objective
function p-norm x p [2] [3]
x 0 x 1 x 2 x 4
• Use other RKHS function
• Incorporate CS for Sparse prior assumptions
8 / 24

13. Computer Aided Medical Procedures | Technische Universität München
Compressive Sensing (CS)
• Objective: Reconstruct a signal z from a small series of
measurements y = CPx, where C is a sensing matrix, P a known
basis and x is sparse
• Solve
argmin
x
x 0 s.t. y = CPx
• When the sparsity is known, this becomes
argmin
x
y − CPx 2
2 s.t. x 0 < L
• Blind compressive sensing can be viewed as a dictionary learning
problem with D = CP
• DL returns D, whereas in BCS you are interested in z = Px
9 / 24

14. Computer Aided Medical Procedures | Technische Universität München
Dictionary Learning (DL) – Overview
• Belongs to class of representation learning algorithms
• Dictionary-learning is a patch-based approach
• It is unsupervised (supervised extensions exist)
• A signal is represented by linear combination of code words
(atoms, basis)
• The basis (dictionary) is overcomplete and the coefficients are
sparse (xi ≈ Dαi )
• The key idea is that a clean image patch can be sparsely
represented by an image dictionary, but the noise cannot
10 / 24

15. Computer Aided Medical Procedures | Technische Universität München
Dictionary Learning
Sparse PCA
=
Y D X
• Sparse Dictionary
Dictionary Learning
=
Y D X
• Sparse coefficients
Definition (Dictionary Learning)
argmin
D,α
1
2
X − Dα 2
F s.t. ∀i, αi 0 ≤ L
11 / 24

16. Computer Aided Medical Procedures | Technische Universität München
Dictionary Learning - Sparse Representation
Notation
• x ∈ Rn is the signal
• D ∈ Rn×K is some overcomplete basis (K > n) with atoms/words
dk ∈ Rn and dk = 1 ∀k
• α ∈ RK is the sparse code of the signal x
• P(·) is a sparsity promoting penalty function
• Objective: Find sparse code α, such that x = Dα
Definition (Sparse Linear Model)
argmin
α
1
2
x − Dα 2
2 + λP(α)
12 / 24

17. Computer Aided Medical Procedures | Technische Universität München
Sparsity Promoting Penalty Functions
Definition ( 0 norm)
P(α) = α 0
Definition ( 1 norm)
P(α) = α 1
Definition (Elastic Net)
Pc(α) = c α 1 + (1 − c)
1
2
α 2
2
13 / 24

18. Computer Aided Medical Procedures | Technische Universität München
Orthogonal Matching Pursuit (OMP)
• Objective Function: argminα
1
2 x − Dα 2
2 s.t. α 0 ≤ L
• Problem is NP-hard, use greedy method instead
• Initialization:
◦ S = ∅ (support)
◦ r ← x (residuals)
• Repeat until convergence:
1. Selection Step:
k∗
← argmax
k
| r, dk | , S ← S ∪ {k∗
}
2. Update Step:
αS ← argmin
αS
x − DSαS
2
2, r ← x − DSαS
14 / 24

19. Computer Aided Medical Procedures | Technische Universität München
OMP – Update Step
• Again, it can be solved by the closed form solution of LSE
αS = DT
S DS
−1
DT
S y. However, the update step is expensive.
• DT
S DS is symmetric positive-definite and updated by appending a
single row and column
• Its Cholesky factorization requires only the computation of its last
row
• For a large set of signals, Batch-OMP can be used [4]
15 / 24

20. Computer Aided Medical Procedures | Technische Universität München
K-SVD [5]
• Dictionary learning problem is both non-convex and non-smooth
• Minimize objective function iteratively by
1. fixing D and finding the best sparse codes α
2. updating one atom dk at a time, while keeping all other atoms fixed,
and changing its non-zero coefficients at the same time (support does
not change)
• Pruning step:
◦ Eliminate atoms that are too close to each other
◦ Eliminate atoms that are used by less than b training examples
◦ Replace them with least explained samples
16 / 24

21. Computer Aided Medical Procedures | Technische Universität München
K-SVD – Dictionary Update
x − Dα 2
F = X −
K
j=1
djαj
T
2
F
=

X −
K
j=k
djαj
T

 − dkαk
T
2
F
= Ek − dkαk
T
2
F
• Fix α and D expect the k-th atom dk, which we want to update
• dkαk
T is a rank-1 matrix ⇒ use SVD
• However, approximating Ek directly would likely remove sparsity
from αk
T
• Solution: Only update coefficients I that correspond to training
examples that use atom dk
17 / 24

22. Computer Aided Medical Procedures | Technische Universität München
K-SVD – Algorithm
input : Example data X ∈ Rn×N
output: Dictionary D ∈ Rn×K
Randomly initialize D;
repeat
for i = 1 to N do
Solve minαi xi − Dαi
2
2 using a sparse coding algorithm (e.g.
OMP, LASSP, or FISTA);
end
for k = 1 to K do
I ← {j|αkj = 0} ; /* Examples that use atom k */
ER
k ← X:,I − j=k djαj,I /* Restricted error matrix */
Apply SVD decomposition ER
k = UΛVT ;
dk ← U:,1 ; /* Update k-th atom */
α:,I ← V:,1Λ(1, 1) ; /* Update sparse codes */
end
until convergence;
18 / 24

23. Computer Aided Medical Procedures | Technische Universität München
K-Means
• K-Means algorithm:
1. Sparse coding update: Partition training examples X into K sets Rk
(k = 1, . . . K)
2. Dictionary update: dk = 1
|Rk | i∈Rk
xi
• If sparsity constrained L = 1
◦ ER
k = X:,I − j=k dj αj,I = X:,I
◦ Updates of atoms become independent of each other
• Limiting the non-zero elements of α to be 1, X:,I is approximated
by a rank-1 matrix dk · 1L
• The solution is the mean of the columns of X:,I
• Conclusion: K-SVD generalizes K-means in which signals are
represented by a linear combination of code words instead of its
cluster centroids
19 / 24

24. Computer Aided Medical Procedures | Technische Universität München
DL-Extensions
• Positively constrained dictionary and/or sparse codes
• Replace 0 constraint by 1, 2, elastic net or structured sparsity
inducing regularizers
• Online dictionary learning
• Discriminative dictionary learning
1. Learn multiple category-specific dictionaries
2. Incorporate discriminative terms into the objective function during
training
argmin
D,α,W
X−Dα 2
F +
i
L(hi , f (αi , W))+λ1 W 2
F s.t. ∀i, αi 0 ≤ L
20 / 24

25. Computer Aided Medical Procedures | Technische Universität München
Graph - Overview
• Fully connected, undirected, and wighted graph with N vertices
• which corresponds to a patch-wise sample in X
• The graph is represented by G = {ν, ε, ω}, where ν is a set of
vertices N, ε is a set of edges, and ω is a set of weights are
assigned using a heat kernel as follows to build the Adjacency
matrix W
Wij =



e−
xi −xj
2
2
σ2 eij ∈ ε
0 else
• The degree matrix D, where its diagonal elements Dij = j Wij
21 / 24

26. Computer Aided Medical Procedures | Technische Universität München
Graph Sparse Coding (GraphSC) [6]
• Build up the Normalized Laplacian Matrix ˜L from the transition
one Lt = D−1W
Definition (GraphSC)
argmin
D,α
1
2
x − Dα 2
2 + λ α 0 + Tr(αT ˜Lα)
GraphSC-Extension
• Incorporate semi-supervised discriminative classification [7]
•
22 / 24

27. Computer Aided Medical Procedures | Technische Universität München
Software
• SPAMS (C++, Matlab, R, Python):
http://spams-devel.gforge.inria.fr/
• CAMP GitLab (C++):
https://campgit.in.tum.de/learning/dictionary
23 / 24

28. Computer Aided Medical Procedures | Technische Universität München
References (1)
Hadamard, J.: Sur les problémes aux dérivés partielles et leur signification physique. Princeton University
Bulletin. pp. 49 – 52. (1902).
Albarqouni, S.: Sparsity Based Regulariztion, http://campar.in.tum.de/Chair/SBR
Albarqouni, S., Lasser, T., Alkhaldi, W., Al-Amoudi, A., Navab, N.: Gradient Projection for Regularized
Cryo-Electron Tomographic Reconstruction Proceedings of MICCAI Workshop on Computational Methods for
Molecular Imaging (CMMI), Boston, MA, USA, September 2014
Rubinstein, Ron and Zibulevsky, Michael and Elad, Michael: Efficient Implementation of the K-SVD Algorithm
using Batch Orthogonal Matching Pursuit. Technical Report CS-2008-08, (2008)
Aharon, M. and Elad, M. and Bruckstein, A.: K -SVD: An Algorithm for Designing Overcomplete Dictionaries
for Sparse Representation. Signal Processing, IEEE Transactions on, 54(11), (2006)
Zheng, M., Bu, J., Chen, C., Wang, C., Zhang, L., Qiu, G., and Cai, D: Graph regularized sparse coding for
image representation. Image Processing, IEEE Transactions on, 20(5), 1327-1336. (2011)
Long, M., Ding, G., Wang, J., Sun, J., Guo, Y., and Yu, P. S: Transfer Sparse Coding for Robust Image
Representation. In Computer Vision and Pattern Recognition (CVPR), 2013 IEEE Conference on (pp. 407-414).
IEEE.
24 / 24