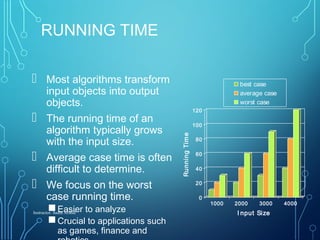
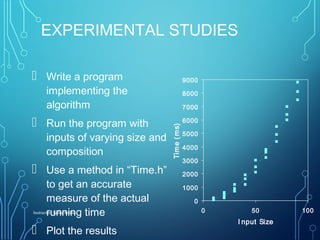
This document provides an overview of an algorithms analysis course. It discusses key topics that will be covered like complexity measures, algorithm structures, efficiency, and data structures. Assignments, projects, and exams will be used for grading. Common problems like sorting and searching will be analyzed along with data structures like arrays, linked lists, stacks, queues, graphs, and trees. The goal is to prepare students to analyze algorithms, compare their efficiency, and design optimized solutions.













![NON-AMBIGUITY
The operations in an algorithm must be rigorously specified:
• At the execution of each step one have to know exactly which is the
next step which will be executed
Example:
Step 1: Set x to value 0
Step 2: Either increment x with 1 or decrement x with 1
Step 3: If x∈[-2,2] then go to Step 2; else Stop.
As long as does not exist a criterion by which one can decide if
x is incremented or decremented, the sequence above cannot be
Instructor: Sadia Arshid](https://image.slidesharecdn.com/01-introtoalgorithm-updated2015-150601060754-lva1-app6891/85/01-intro-to-algorithm-updated-2015-15-320.jpg)
![NON-AMBIGUITY (CONT’D)
Let’s modify the previous algorithm as follows:
Step 1: Set x to value 0
Step 2: Flip a coin
Step 3: If one obtains head
then increment x with 1
else decrement x with 1
Step 3: If x∈[-2,2] then go to Step 2, else Stop.
• This time the algorithm can be executed but … different executions can be
different
Instructor: Sadia Arshid](https://image.slidesharecdn.com/01-introtoalgorithm-updated2015-150601060754-lva1-app6891/85/01-intro-to-algorithm-updated-2015-16-320.jpg)











![EXAMPLE
Instructor: Sadia Arshid
Algorithm arrayMax(A, n)
Input array A of n integers
Output maximum element of A
currentMax ← A[0]
for i ← 1 to n − 1 do
if A[i] > currentMax then
currentMax ← A[i]
return currentMax
Example: find max element of
an array](https://image.slidesharecdn.com/01-introtoalgorithm-updated2015-150601060754-lva1-app6891/85/01-intro-to-algorithm-updated-2015-30-320.jpg)
![COUNTING PRIMITIVE
OPERATIONS
By inspecting the pseudocode, we can determine the
maximum number of primitive operations executed by an
algorithm, as a function of the input size
AlgorithmarrayMax(A, n) # operations
currentMax ← A[0] 2
fori ← 1 to n − 1 do 1 + n
if A[i] > currentMax then 2(n − 1)
currentMax ← A[i] 2(n − 1)
{ increment counter i } 2(n − 1)
return currentMax 1
Total 7n − 2
Instructor: Sadia Arshid](https://image.slidesharecdn.com/01-introtoalgorithm-updated2015-150601060754-lva1-app6891/85/01-intro-to-algorithm-updated-2015-31-320.jpg)



