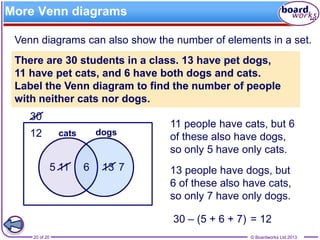
The document provides an overview of sets in mathematics, discussing elements, unions, intersections, and complements. It explains key concepts such as disjoint sets, subsets, and the universal set, illustrated with various examples. Additionally, it mentions how to represent these concepts through Venn diagrams and calculates the number of elements in sets.

1. This icon indicates the slide contains activities created in Flash. These activities are not editable.
For more detailed instructions, see the Getting Started presentation.
This icon indicates an accompanying worksheet.
This icon indicates teacher’s notes in the
Notes field.
© Boardworks Ltd 20131 of 20

2. © Boardworks Ltd 20132 of 20

3. © Boardworks Ltd 20133 of 20
A set consists of objects or elements. The elements can be
numbers, letters, etc. Elements are listed inside curly brackets.
Sets can have a finite or infinite number of elements, or they
can be empty. Sets with no elements, { }, are called the
empty set, or the null set, and are denoted by the symbol ∅.
A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
is a set of single digit positive numbers.
B = {red, yellow, blue}
is the set of primary colours.
Sets and elements

4. © Boardworks Ltd 20134 of 20
Defining sets
C = {x : 0 < x < 5}
As well as listing all the elements, sets can be defined by
describing them algebraically.
“C is the set of all elements x such that 0 is
less than x and x is less than 5.”
This could also be written with a vertical line instead
of a colon, C = {x | 0 < x < 5}.

5. © Boardworks Ltd 20135 of 20
Universal set
The universal set, ξ, is the largest possible set for a scenario.
When needed in a problem, the universal set is normally given.
3 ∈ {odd numbers} means “3 belongs to the set of
odd numbers.”
What does 2 ∉ {odd numbers} mean?
2 does not belong to the set of odd numbers.
For example, when we talk about even and odd numbers,
the universal set is the natural numbers.
In a given scenario, there is a limit to the type of objects that
could be in a set.

6. © Boardworks Ltd 20136 of 20

7. © Boardworks Ltd 20137 of 20
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
Unions
The union of two or more sets contains all the elements in all
the sets. The union of sets A and B is the elements in either
set A or B or both.
Unions of sets are denoted by the symbol ∪.
A = {1, 2, 3, 4, 5, 6}
B = {7, 8, 9, 10, 11}
A = {outcomes of rolling a die}
B = {positive integers between and inclusive of 7 and 11}
List the elements in A ∪ B.

8. © Boardworks Ltd 20138 of 20
Intersections
The intersection of two or more sets contains the elements
that are in all the sets.
For example, the elements in both set A and B.
Intersections of sets are denoted by the symbol ∩.
A = {outcomes of rolling a die}
B = {positive integers between and inclusive of 4 and 9}
List the elements in A ∩ B.
A = {1, 2, 3, 4, 5, 6}
B = {4, 5, 6, 7, 8, 9}
A ∩ B = {4, 5, 6}

9. © Boardworks Ltd 20139 of 20
Disjoint sets
Disjoint sets are two or more sets that have no elements
in common, therefore the intersection is an empty set.
For example, A = {all 3-D shapes with a curved surface},
and B = {all polyhedrons}, are disjoint sets.
The intersection of disjoint sets is the empty set:
A ∩ B = ∅

10. © Boardworks Ltd 201310 of 20
True or false

11. © Boardworks Ltd 201311 of 20

12. © Boardworks Ltd 201312 of 20
Complement
The complement of a set is all of the elements in the
universal set but not in the set of interest.
Complements of sets are denoted using a prime symbol ′.
What is the complement of the set of even outcomes
when rolling a die?
universal set:
set of even outcomes:
complement of set:
ξ = {1, 2, 3, 4, 5, 6}
E = {2, 4, 6}
E′ = {1, 3, 5}, the set of possible odd
outcomes.

13. © Boardworks Ltd 201313 of 20
Venn diagram

14. © Boardworks Ltd 201314 of 20
Language of sets

15. © Boardworks Ltd 201315 of 20
Subsets
B is a subset of A, because it contains some of the elements
of A. B ⊆ A means B is a subset of A.
B = {2, 4, 6}
What is the set of possible even
outcomes?
A = {1, 2, 3, 4, 5, 6}
What is the set of possible outcomes
from rolling a die?
It is a proper subset, because it does not have exactly the
same elements as A. This is written B ⊂ A.
Every set is a subset of itself. A ⊆ A but A ⊄ A.

16. © Boardworks Ltd 201316 of 20
Unions and intersections
Let A be the set of all letters in the English alphabet.
Let B be the set of all vowels in the alphabet.
Let C be the set of all letters in your name.
Draw a Venn diagram to represent these sets.
What is the universal set and which are subsets?
A is the universal set.
B is a subset of A.
C is a subset of A.
Describe B'.
B′ is the set of all consonants in the English alphabet.
List the elements in B ∩ C and B ∪ C.

17. © Boardworks Ltd 201317 of 20
Triple Venn diagram

18. © Boardworks Ltd 201318 of 20
Sets in the animal kingdom

19. © Boardworks Ltd 201319 of 20
Number of elements
The number of elements in a set, A, is written n(A).
For example, if A = {2, 4, 6, 8, 10}, then n(A) = 5.
Let ξ = {students in year 10}, A = {students who play
football} and B = {students who play tennis}.
If ∅ = { }, what is n(∅)? n(∅) = 0
If n(A) = 40, n(A ∩ B) = 14, and n(A ∪ B) = 52, then how
many students play tennis?
Students who play only tennis: 52 – 40 = 12
Students who play tennis and football: 14
Total students who play tennis: 12 + 14 = 26

20. © Boardworks Ltd 201320 of 20
More Venn diagrams
Venn diagrams can also show the number of elements in a set.
There are 30 students in a class. 13 have pet dogs,
11 have pet cats, and 6 have both dogs and cats.
Label the Venn diagram to find the number of people
with neither cats nor dogs.
30
11 136 75
11 people have cats, but 6
of these also have dogs,
so only 5 have only cats.
13 people have dogs, but
6 of these also have cats,
so only 7 have only dogs.
12
30 – (5 + 6 + 7) = 12