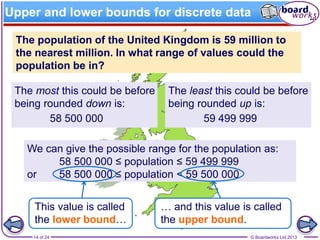
The document discusses the concept of rounding numbers, explaining various methods such as rounding to the nearest whole number, decimal places, and significant figures. It also differentiates between discrete and continuous quantities, providing examples of how upper and lower bounds can be established based on rounding. Additionally, it includes practical applications of these concepts in scenarios like measuring heights and calculating profits.