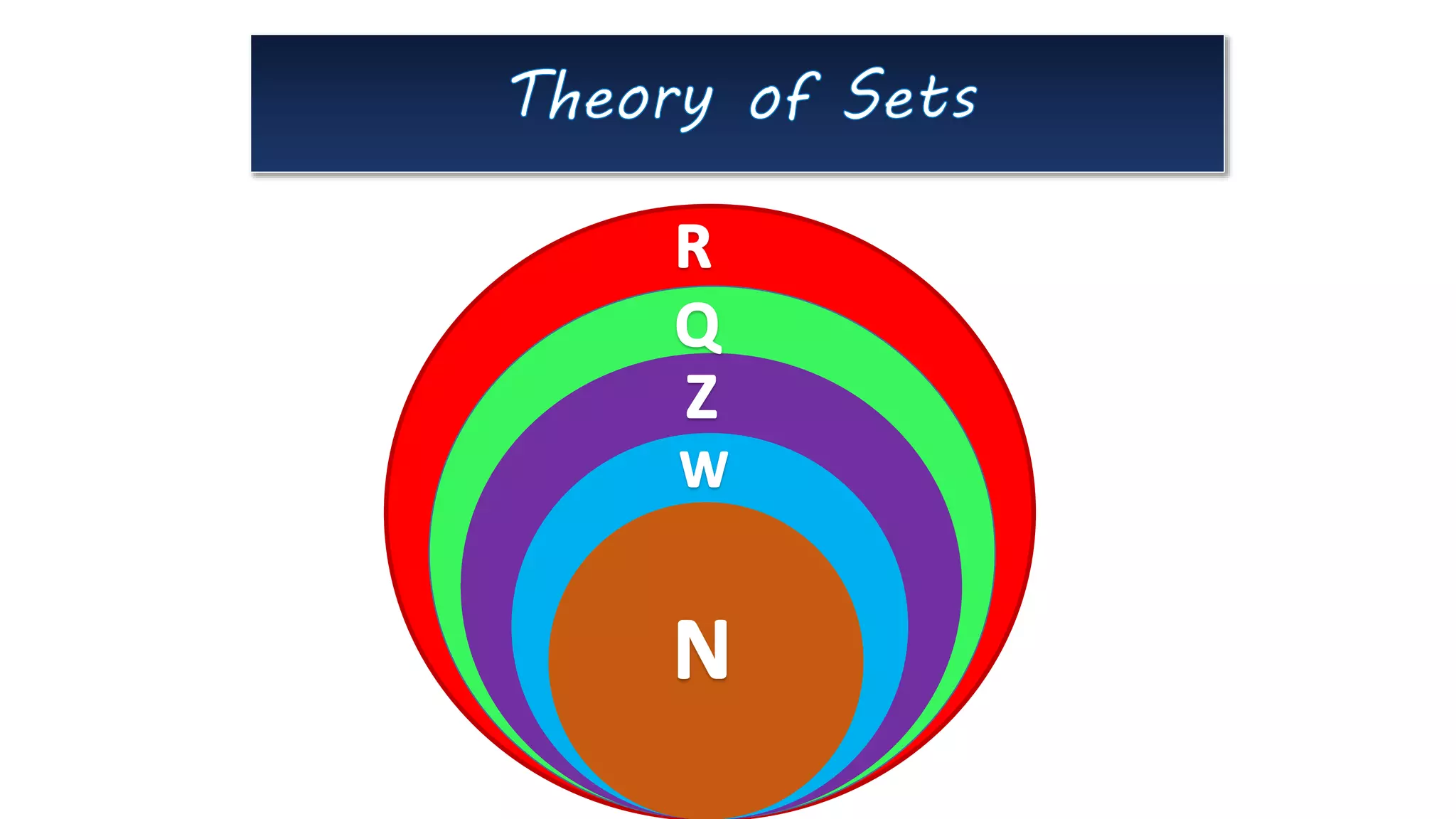
This document discusses sets and set operations. It defines key concepts such as: - Sets can be represented in descriptive form, set builder form, and roster form. - Universal sets, subsets, proper subsets, power sets, unions, intersections, complements, disjoint sets, differences, and symmetric differences of sets. - Examples of how to use formulas involving sets and set operations to solve problems, such as finding the size of an intersection given other set information.

2. Main Targets
• To describe a set
• To represent sets in descriptive form, set builder form and roster form
• To identify different kinds of sets
• To understand and perform set operations
• To use Venn diagrams to represent sets and set operations
• To use the formula involving n (A U B) simple world problems

3. Key Concept Set
A set is a collection of well defined objects. The objects of a set are called elements or
members of th set.
Which of the following collections are well defined?
(1) The collection of male students in your class.
(2) The collection of numbers 2, 4, 6, 10, and 12.
(3) The collection od districts in Tamil Nadu.
(4) The collection of all good movies.

4. Set are named with the capital letters A, B, C, etc.
The elements of a set are
Denoted by the small letters, a, b, c, etc.

5. For example,
Consider the set A= 1, 3, 5, 9
1 is an element of A, written as 1 є A
3 is an element of A, written as 3 є A
8 is not an element of A, written as 8 є A

6. Reading Notation
If x is an element of a set A, we write x є A
If x is not an element of the set A, we write x є A.
є ‘ is an element of’ or ‘belongs to’
є ‘ is not an element of’ or does not belong to’

7. Descriptive Form Set Builder Form Roster Form
The set of all vowels in
English alphabet
𝑥 ∶ 𝑥 𝑖𝑠 𝑎 𝑣𝑜𝑤𝑒𝑙 𝑖𝑛 𝑡ℎ𝑒
𝐸𝑛𝑔𝑙𝑖𝑠ℎ 𝑎𝑙𝑝ℎ𝑎𝑏𝑒𝑡
𝑎, 𝑒, 𝑖, 𝑜, 𝑢
The set of all odd positive integers
less than or equal to 15
𝑥 ∶ 𝑥 𝑖𝑠 𝑎𝑛 𝑜𝑑𝑑 𝑛𝑢𝑚𝑏𝑒𝑟
𝑎𝑛𝑑 0 < 𝑥 ≤ 15
1,2,5,7,9,11,13,15
The set of all positive cube numbers
less than 100
𝑥 ∶ 𝑥 𝑖𝑠 𝑎 𝑐𝑢𝑏𝑒 𝑛𝑢𝑚𝑏𝑒𝑟
𝑎𝑛𝑑 0 < 𝑥 < 100
1,8,27,64
Representation of sets in Different Forms

8. Key Concept Empty Set
A set containing no elements is called the empty set or null set or void set.
The empty set is denoted by the symbol ∅ or { }
Reading Notation
Empty set o Null set or Void set∅ or { }

9. Consider the set A = {x: x <1, x є N}.
There is no natural number which is less than 1.
∴ A= { }
Note
The concept of empty set plays a key role in the study of sets just like
the role of the number system.

10. Key Concept finite Set
If the number of elements in a set is zero or finite, then the set is called a finite set.
Consider the set X= {x : x is an integer and -1≤ x ≤ 2}
𝑋 = −1,0,1,2 and 𝑛 𝑋 = 4
∴ X is a finite set
Finite Set

11. Key Concept Infinite Set
A set is said to be an infinite if the number of elements in the set is not finite.
Infinite Set
Let W= the set of all whole numbers. i. E., W = {0,1,2,3 ...}
The set of all whole numbers contain infinite number of elements
∴ W is an infinite set.
Note The cardinal number of an infinite set is not a finite number

12. Equivalent Set
Key Concept Equivalent Set
Two sets A and B are said to be equivalent if they have the same number of elements
In other words, A and B are equivalent if n (A)= n (B).
‘A and B are equivalent’ is written as A ≈ 𝑩
Reading Notation
≈ Equivalent
For example :
Consider the set A= {3,5,6,11}.
Here n (A)=4 and (B)=4 ∴ A ≈ 𝑩
Equivalent Set
Key Concept Equivalent Set

13. Equal Sets
Key Concept Equal Sets
Two sets A and B are said to be equal if they contain exactly the same elements,
regardless of order. Otherwise the sets are said to be unequal.
In other words,two sets A and B are said o be equal if
(i) Every element of A is also an element of B and
(ii) Every element of B is also an element of A.
Reading Notation

14. Subset
Key Concept Equal Sets
A set X is a subset of Y if every element of X is also an element of Y.
In symbol we write X ⊆ 𝑌
Read X ⊆ 𝑌 as ‘X is a subset of Y’ or’X is contained in Y’
Read X ⊈ 𝑌 as ‘X is not a subset of Y’ or’X is not contained in Y’
Reading Notation
⊆
⊈

15. For example :
Consider the sets
X = {7,8,9} and Y = 7,8,9 10
We see that every element of X is also an element of Y.
∴X is a subset of Y
i.e X ⊆ Y.
Note
(i) Every set is a subset of itself i.e X ⊆ Y for any set X
(ii) The empty set is a subset of any set i.e., ∅ ⊆ X, for any set X
(iii) If X Y and Y ⊆ X, then X=Y. The converse is also i.e.if X=Y then
X ⊆ Y and Y ⊆ X
(iv) Every set (expect ∅) has atleast two subsets, ∅ and set itself

16. A set X is said to be a proper subset of set Y if X ⊆ Y and X ≠ 𝑌. 𝐼𝑛 𝑠𝑦𝑚𝑏𝑜𝑙 we
write X ⊆ Y . Y is called super set of X
Read X ⊂ Y as X is a proper subset of Y
Reading Notation
Proper Set
Key Concept Proper subset set
⊂

17. The set of all subset of A is said to be power set of the set A.
Read X ⊂ Y as X is a proper subset of Y
The power set of a set A is denoted by P(A)
Reading Notation
Power Set
Key Concept Power set
P (A)

19. We use diagrams or pictures in
geometry to explain a concept or a situation
sometimes we also use them to solve
problems. In mathematics, we use
diagrammatic representations called Venn
Diagrams to visualize the relationships
between sets and set operations.

20. John Venn (1834-1883) a British
mathematician used diagrammatic
representation as an aid to visualize
varios relationships between sets and
set operation

21. The set that contains all the under consideration in agiven discusssion is
called the universal set. The universal set is a denoted by U or E.
Key Concept Universal set

22. The set that contains elements of U (universal set) that are alements of
A ⊆ 𝑈 is called the compliment of A. The complement of aA is denoted by
𝐴′
𝑜𝑟 𝐴 𝑐
Key Concept Complement set
Reading Notation
𝑨′ {x: x ∈ 𝑼 𝒂𝒏𝒅 𝑿 ∉ 𝑨}.

23. The union set of two sets A and B is the element which are in A or in B
or both A and B. we write the union of sets A and B as A ∪ 𝐵.
Read A ∪ 𝐵 as ‘A union B’
In symbol, A ∪ 𝐵={ x:x ∈ 𝐴 𝑜𝑟 𝑥 ∈ B}
Key Concept Union set
Reading Notation
∪

24. The intersection of two sets A and B is the set of all elements common
to A and B. We denoted A ∩ 𝐵.
Read A ∩ 𝐵 as ‘A intersection B’
Symbolically , we write A∩ 𝐵={ x:x ∈ 𝐴 𝑜𝑟 𝑥 ∈ B}
Key Concept Intersection of set
Reading Notation
∩
Intersection of Two Set

25. Two sets A and B are said to be disjoint if there is no element
common to both A and B
In other words, If A and are disjoint sets, then A ∩ 𝐵 = ∅
Key Concept Disjoint Sets
Disjoint Sets

26. Key Concept Difference of two sets
Diferrence of Two Sets
The difference of the two sets A and B is the set of all elements belonging to a A bur
not to B. The difference of thw two sets is denoted by A – B or AB.
In symbol, we write : A 0 B= { x: x ∈ 𝐴 𝑜𝑟 𝑥 ∉ B}
Similarly, we write: B –A = { x: x ∈ 𝐵 𝑜𝑟 𝑥 ∉ 𝐀}
Reading Notation

27. Key Concept Symmetric Difference of sets
Symmetric Difference of Sets
Tthe symmetric difference of two sets A and B is the union of their diffferences and
is denoted by
Thus,
Reading Notation

28. For Any finite setd A and B, We have the following useful results
(i) 𝒏 𝑨 = 𝒏 𝑨 − 𝑩 + 𝑨 ∩ 𝑩
(ii) 𝒏 𝑩 = 𝒏 𝑩 − 𝑨 + 𝒏 𝑨 ∩ 𝑩
(iii) 𝒏 𝑨 ∩ 𝑩 = 𝐧 𝐀 − 𝐁 + 𝒏 𝑨 ∩ 𝑩 + 𝐧 𝐁 − 𝐀
(iv) 𝒏 𝑨 ∩ 𝑩 = n(A)+n(B) - 𝒏 𝑨 ∩ 𝑩
(v) 𝒏 𝑨 ∩ 𝑩 = 𝐧 𝐀 + 𝐧 𝐁 , 𝐰𝐡𝐞𝐧 𝑨 ∩ 𝑩 = ∅
(vi) 𝒏 𝑨 + 𝒏 𝑨′
= 𝒏(𝑼)
Important Results

29. If 𝒏 𝑨 = 𝟏𝟐, 𝒏 𝑩 = 𝟏𝟕 𝒂𝒏𝒅 𝒏 𝑨 ∪ 𝑩 = 𝟐𝟏, 𝒇𝒊𝒏𝒅 𝒏 𝑨 ∩ 𝑩
Solution: Given that 𝒏 𝑨 = 𝟏𝟐, 𝒏 𝑩 = 𝟏𝟕 𝒂𝒏𝒅 𝒏 𝑨 ∪ 𝑩 = 𝟐𝟏
By using the formula 𝒏 𝑨 ∪ 𝑩 = 𝒏 𝑨 + 𝒏 𝑩 − 𝒏 𝑨 ∩ 𝑩
𝒏 𝑨 ∩ 𝑩 = 𝟏𝟐 + 𝟏𝟕 − 𝟐𝟏 = 𝟖
Example:

30. In a city 65% of the people view Tamil movies and 40% view English
movies, 20% of the people view both Tamil and English movies. Find the
percentage of people do not view any of these two movies
Example: