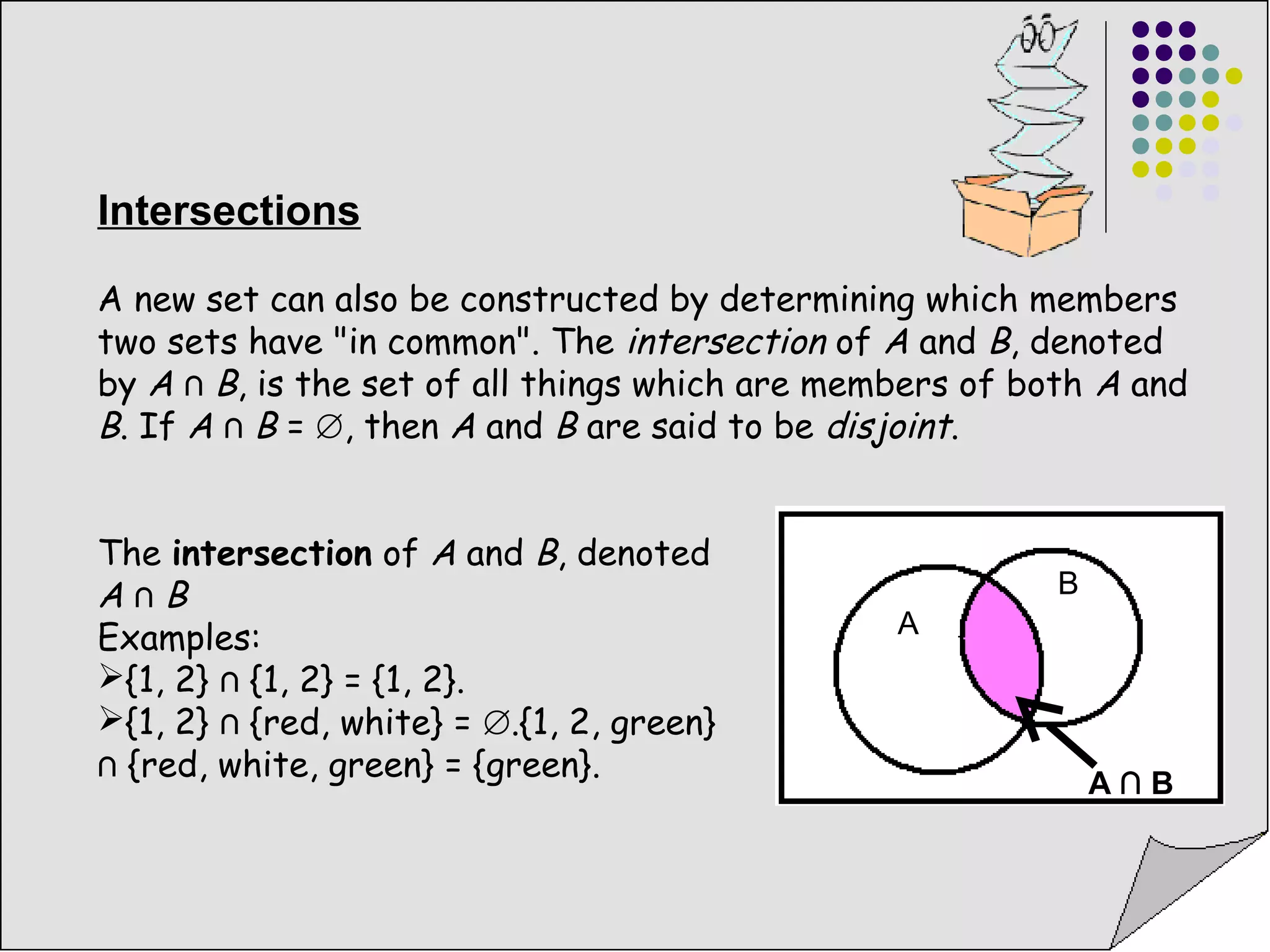
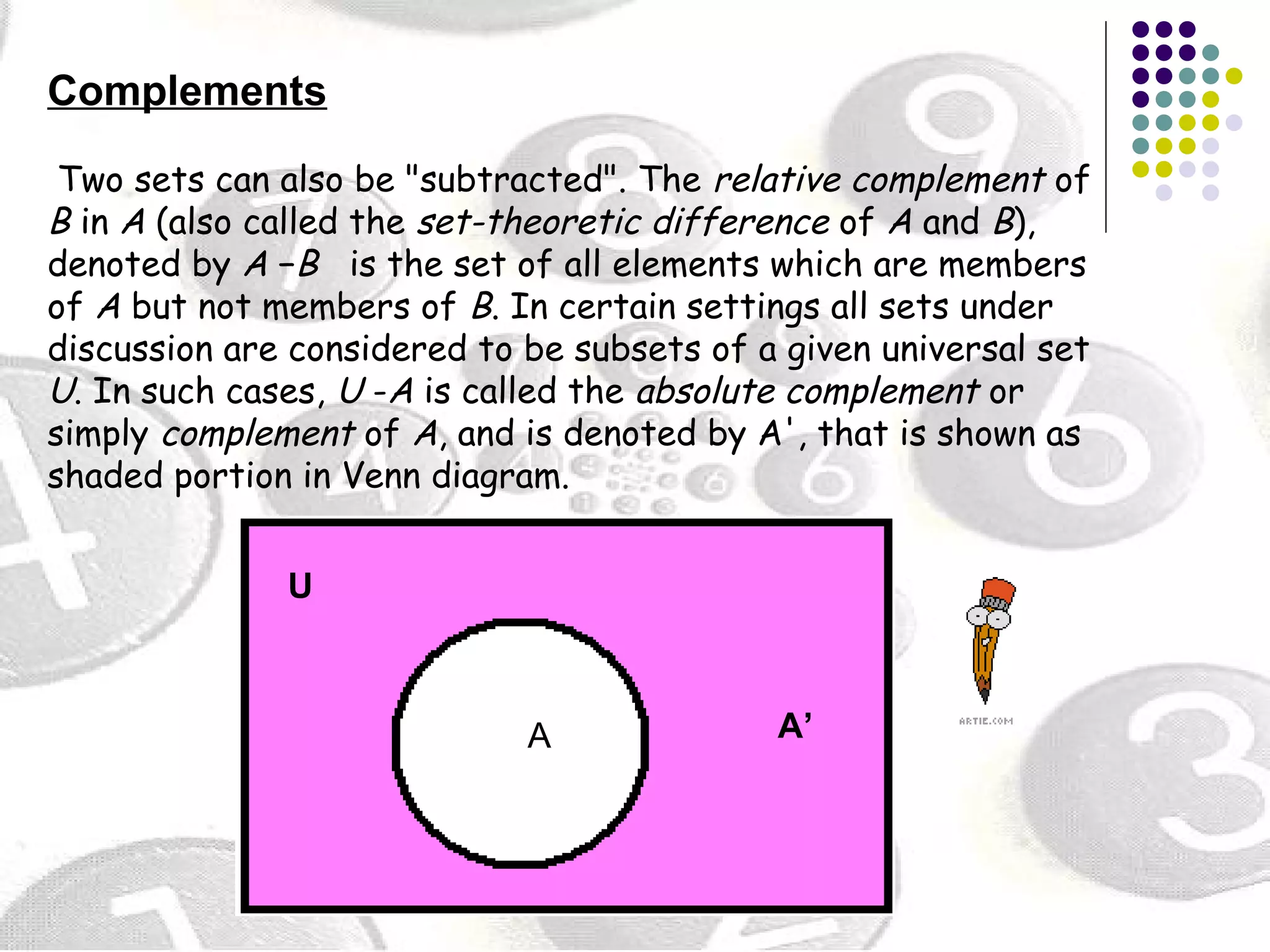
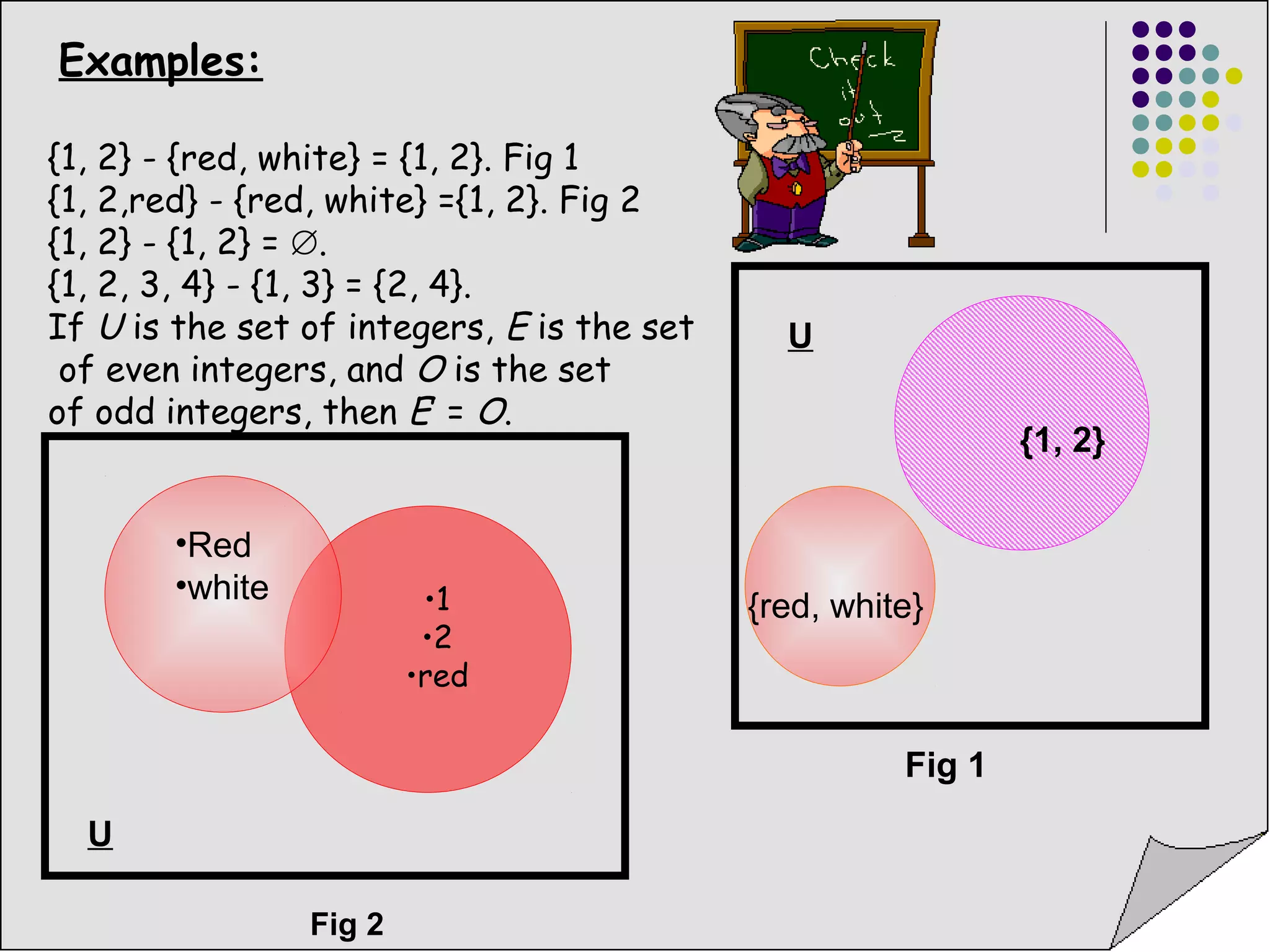
The document discusses key concepts in set theory including: 1) Sets are collections of distinct objects that are considered as a single object. Set theory was invented by George Cantor in the late 19th century. 2) There are different ways to represent sets including roaster form using curly brackets, set builder form using properties, and Venn diagrams using circles. 3) Set operations include unions, intersections, and complements which combine sets in different ways according to their members.

1. A
B C
Made by
Anshika Singh,
Mansi Bhatia &
Payal Batra
XI F

2. A set is a collection of distinct objects, considered as an
object in its own right.
Theory of sets wwaass iinnvveenntteedd bbyy
GGeeoorrggee CCaannttoorr iinn eenndd ooff
nniinneetteeeenntthh cceennttuurryy..
F o r e x a m p l e c o l l e c t i o n o f
b e s t t e a c h e r s o f a s c h o o l
i s n o t d e f i n e d t h u s , i t i s
n o t a s e t w h e r e a s
c o l l e c t i o n o f m o s t
e x p e r i e n c e d t e a c h e r s c a n
b e d e f i n e d a n d i t i s a s e t .

3. Roaster form
Roaster form is notated by enclosing the list of members in
braces.
Roaster form of A is the set whose members
are the first four positive integers is {1,2,3,4}.
All set operations preserve the property that each element of the set
is unique. The order in which the elements of a set are listed is
irrelevant, unlike a sequence. For example,
{6, 11} = {11, 6} = {11, 11, 6, 11}

4. Set builder form
 In set-builder form, all the members of a set has a single common
Property which is not possessed by any other element outside the set.
E = {playing card suits} is the set whose four members are ♠,
♦, ♥, and ♣.
The set F of the twenty smallest integers that are
four less than perfect squares can be denoted:
F = {n2 − 4 : n is an integer; and 0 ≤ n ≤ 19}
In this notation, the colon (":") means "such that", and the
description can be interpreted as "F is the set of all numbers
of the form n2 − 4, such that n is a whole number in the
range from 0 to 19 inclusive." Sometimes the vertical bar
("|") is used instead of the colon.

5. The Empty set
the empty set is the unique set having no
elements; its size is zero. Many possible
properties of sets are trivially true for the
empty set. Common notations for the empty set
include "{},“ and “ ". The latter two symbols
were introduced by the Bourbaki group
(specifically Andre Weil) in 1939, inspired by
the letter Ø in the Danish and Norwegian
alphabet Other notations for the empty set
include "Λ", "0 it is also called void set or null
set.

6. For example Consider the set
A = { x : x is a student presently studying in both Classes II and I }
We observe that a student cannot study simultaneously in
both Classes I and II. Thus, the set A contains no element
at all. It is empty set, null set or void set.
Equal sets
When every element of set A is present in set B and
vice versa then A and B are called equal sets.
we write A = B. Otherwise, the sets are said to be unequal
and we write A ≠ B.
We consider the following examples :
(i) Let A = {1, 2, 3, 4} and B = {3, 1, 4, 2}. Then A = B.
(ii) Let A be the set of two consecutive natural numbers less
than 6 and P the set of prime factors of 20. Then A and P are
equal, since 4 and 5are the only prime factors of 20 and also
these are less than 6.

7. Finite and Infinite Sets
Finite set is a set that has a finite number of
elements.
For example,
is a finite set with five elements. The number of elements of
a finite set is a natural number (non-negative integer), and is
called the cardinality of the set. A set that is not finite is
called infinite. For example, the set of all positive integers is
infinite:

8. Venn diagrams or set diagrams are diagrams that
show all hypothetically possible logical relations
between a finite collection of sets (groups of
things) The universal set is represented usually by
a rectangle and its subsets by circles. Venn
diagrams were conceived around 1880 by John Venn.
They are used to teach elementary set theory, as
well as illustrate simple set relationships in
probability, logic, statistics, linguistics and
computer science.

9. If every member of set A is also a member of set B, then A is
said to be a subset of B, written A ⊊ B (also pronounced A is
contained in B). Equivalently, we can write B ⊊ A, read as B is a
superset of A, B includes A, or B contains A. The relationship
between sets established by ⊊ is called inclusion or containment.
B
A
For example
set of all girls of a school is
subset set of all students of
that school.
{1, 3} ⊊ {1, 2, 3, 4}.
{1, 2, 3, 4} ⊊ {1, 2, 3, 4}.
U

10. A universal set is the set of all elements under consideration, ... The
elements of sets A and B can only be selected from the given universal
set U .
A
A’
U

11. The power set of S, written , P(S), ℘(S) or 2S, is the set of all
subsets of S, including the empty set and S itself. the existence of
the power set of any set is postulated by the axiom of power set.
Any subset F of is called a family of sets over S.
The set of non-empty subsets of S may be denoted by , P1(S) or
similar. for example If S is the set {x, y, z}, then the subsets of S
are:
{ } (also denoted , the empty set)
{x}
{y}
{z}
{x, y}
{x, z}
{y, z}
{x, y, z}
and hence the power set of S is

12. Unions
A B
The union of A and B, denoted
A UB .Two sets can be "added"
A U B
together. The union of A and B,
denoted by A U B, is the set of all things which are members of
either A or B.
Examples:
{1, 2} {red, white} = {1, 2, red, white}.
{1, 2, green} U {red, white, green} = {1, 2, red, white,
green}.
{1, 2} U {1, 2} = {1, 2}.

13. Intersections
A new set can also be constructed by determining which members
two sets have "in common". The intersection of A and B, denoted
by A ∩ B, is the set of all things which are members of both A and
B. If A ∩ B = ∅, then A and B are said to be disjoint.
The intersection of A and B, denoted
A ∩ B
Examples:
{1, 2} ∩ {1, 2} = {1, 2}.
{1, 2} ∩ {red, white} = ∅.{1, 2, green}
∩ {red, white, green} = {green}.
A
B
A ∩ B

14. Complements
Two sets can also be "subtracted". The relative complement of
B in A (also called the set-theoretic difference of A and B),
denoted by A −B is the set of all elements which are members
of A but not members of B. In certain settings all sets under
discussion are considered to be subsets of a given universal set
U. In such cases, U -A is called the absolute complement or
simply complement of A, and is denoted by A', that is shown as
shaded portion in Venn diagram.
U
A A’

15. Examples:
{1, 2} - {red, white} = {1, 2}. Fig 1
{1, 2,red} - {red, white} ={1, 2}. Fig 2
{1, 2} - {1, 2} = ∅.
{1, 2, 3, 4} - {1, 3} = {2, 4}.
If U is the set of integers, E is the set
of even integers, and O is the set
of odd integers, then E′ = O.
{1, 2}
U
•1 {red, white}
•2
•red
Fig 2
•Red
•white
U
Fig 1

16. Some Properties of Complement Sets
1. Complement laws: (i) A U A′ = U fig 3 (ii) A ∩ A′ = φ
2. De Morgan’s law: (i) (A U B)´ = A′ ∩ B′ (ii) (A ∩ B )′ = A′ ∩B′
3. Law of double complementation : (A′ )′ = A fig 4
4. Laws of empty set and
universal set φ′ = U and U′ = φ.
These laws can be verified by
using Venn diagrams.
U
A’
A
Fig 3
U
(A’)’=A
A’
Fig 4

17. In a survey of 300 children's in a
colony, 225 children's were found to
be taking milkshake and 50 taking
coffee, 100 were taking both
milkshake and coffee. Find how many
students were taking neither
milkshake nor coffee

18. Here n(M) = 225, n(C) = 50, n(M ∩ C) = 100
Also we know that
n(M U C) = n(M) + n(C) – n(T ∩ C)
= 225 + 50 – 100 = 175
Total no. of students = 300
No. of students who neither take milkshake
nor coffee
= 300 – 175 = 125
M 225
C 50
U 300
(M∩C)100