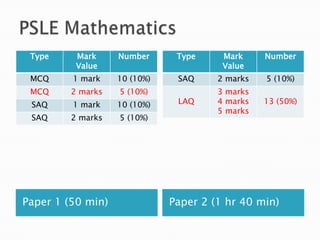
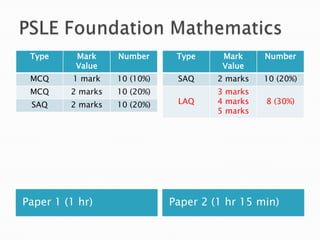
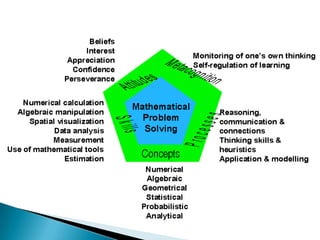
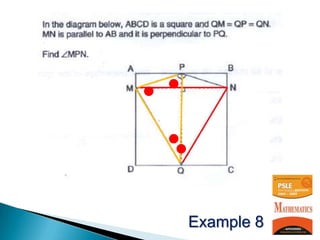
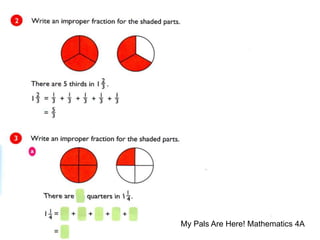
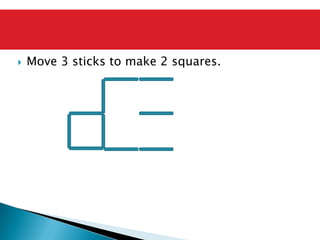
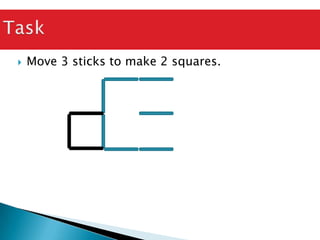
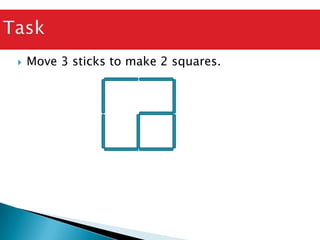
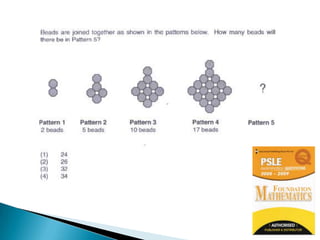
The document discusses the PSLE mathematics curriculum and its emphasis on problem-solving as a key competency. It highlights concerns from parents regarding the difficulty of recent exams, particularly with the introduction of calculators. Additionally, it outlines various teaching strategies and competencies necessary for effective mathematics learning, including visualization and metacognition.

1. PSLE Mathematics SeminarAssociation of Mathematics Educatorshttp://math.nie.edu.sg/ameYeap Ban HarNational Institute of EducationNanyang Technological University banhar.yeap@nie.edu.sg

2. Part 1This section explains the PSLE format.

3. PSLE Mathematics

4. PSLE MathematicsPaper 1 (50 min)Paper 2 (1 hr 40 min)

5. PSLE Foundation MathematicsPaper 1 (1 hr)Paper 2 (1 hr 15 min)

6. Part 2This section explains the curriculum that the PSLE is based on.

7. PSLE Mathematics is Based on a Problem-Solving Curriculum

9. rationale of the curriculumThe rationale of teaching mathematics is that it is “a good vehicle for the development and improvement of a person’s intellectual competence”.

10. Part 3This section explains that problem solving is a basic ability in the PSLE.

11. “Mathematical problem solving is central to mathematics learning.” Ministry of Education 2006

12. Ali paid for a 85-cent pen with a $5 note.How much change should he get?Answer: $__________Example 1

13. A show started at 10.55 a.m. and ended at 1.30 p.m. How long was the show in hours and minutes?Example 2

14. Prawns are sold at $1.35 per 100 g at a market. What is the price of 1.5 kg of prawns? $13.50 + $6.75 = $20.25Example 3

15. During a sale, mugs are sold in sets of 3 for $1.45. How much must Bala pay for buying 15 mugs during the sale?$1.45 x 5 = $14.50 ÷ 2 = $7.25Example 4

16. Sam had 295 eggs. He packed all the eggs into boxes of 9 with some left over. How many eggs are left over? 295 ÷ 9 = (30 + 2) remainder 77 eggs are left overExample 5

17. 29527025

18. Mr Tan rented a car for 3 days. He was charged $155 per day and 60 cents for every km that he travelled. He paid $767.40. What was the total distance that he travelled for the 3 days?$767.40 – 3 x $155 = $302.40$302.40 ÷ 60 cents per km = 504 kmExample 5

19. Mr Tan rented a car for 3 days. He was charged $155 per day and 60 cents for every km that he travelled. He paid $767.40. What was the total distance that he travelled for the 3 days?767.40 – 3 x 155 = 302.40302.40 ÷ 0.60 = 504 He travelled 504 km.Example 5

20. Find <y in the figure below.360o – 210o = 150o70 o70 oy70 oExample 6

21. “Mathematical problem solving is central to mathematics learning.” Ministry of Education 2006

22. Part 4This section explains that there are other competencies in mathematics learning e.g. practical skills.

23. Basic Skillscomputation and procedures is not everything

24. The height of the classroom door is about __.(1) 1 m(2) 2 m(3) 10 m(4) 20 mExample 7

25. Practical Skillswritten examinations may include bits of practical tasksPossibilitiesExampleFind the area of the cover page of the examination paper.

26. Part 5This section explains the key competencies in solving challenging problems.

27. ““… including non-routine, open-ended and real-world problems.”Ministry of Education 2006

28. Example 8

29. Mrs Hoon made some cookies to sell. 3/4 of them were chocolate cookies and the rest were almond cookies. After selling 210 almond cookies and 5/6 of the chocolate cookies, she had 1/5 of the cookies left.How many cookies did Mrs Hoon sell?almond cookies5/83/8210chocolate cookies1/53/8 – 1/5 = 7/40  210 1/40  30Example 1032/40  960She sold 960 cookies.

30. Example 11

31. Parents Up In Arms Over PSLE Mathematics Paper TODAY’S 10 OCT 2009SINGAPORE: The first thing her son did when he came out from the Primary School Leaving Examination (PSLE) maths paper on Thursday this week was to gesture as if he was "slitting his throat". "One look at his face and I thought 'oh no'. I could see that he felt he was condemned," said Mrs Karen Sng. "When he was telling me about how he couldn't answer some of the questions, he got very emotional and started crying. He said his hopes of getting (an) A* are dashed." Not for the first time, parents are up in arms over the PSLE Mathematics paper, which some have described as "unbelievably tough" this year. As recently as two years ago, the PSLE Mathematics paper had also caused a similar uproar. The reason for Thursday's tough paper, opined the seven parents whom MediaCorp spoke to, was because Primary 6 students were allowed to use calculators while solving Paper 2 for the first time. …Said Mrs Vivian Weng: "I think the setters feel it'll be faster for them to compute with a calculator. So the problems they set are much more complex; there are more values, more steps. But it's unfair because this is the first time they can do so and they do not know what to expect!" …"The introduction of the use of calculators does not have any bearing on the difficulty of paper. The use of calculators has been introduced into the primary maths curriculum so as to enhance the teaching and learning of maths by expanding the repertoire of learning activities, to achieve a better balance between the time and effort spent developing problem solving skills and computation skills. Calculators can also help to reduce computational errors." …Another common gripe: There was not enough time for them to complete the paper. A private tutor, who declined to be named, told MediaCorp she concurred with parents' opinions. "This year's paper demanded more from students. It required them to read and understand more complex questions, and go through more steps, so time constraints would have been a concern," the 28-year-old said.

33. chocolatessweets12Jim12121212121818Ken3 parts  12 + 12 + 12 + 12 + 18 = 661 part  22Half of the sweets Ken bought = 22 + 12 = 34So Ken bought 68 sweets.

34. Visualization – an intellectual competence - is one of the most important ability in solving problems

35. Learning Basic Skillsemphasis on visualization in the learning process

37. My Pals Are Here! Mathematics 4A

38. Shaping Maths 2A

39. 

40. 

41. 

42. Shaping Maths 4B

43. Catholic High School (Primary)

44. visualizationWellington Primary School

45. Move 3 sticks to make 2 squares.

46. TaskMove 3 sticks to make 2 squares.

47. TaskMove 3 sticks to make 2 squares.

48. DivisionPhoto: Princess Elizabeth Primary School

49. My Pals Are Here! Mathematics 1B

50. visualizationScarsdale Middle School New York

51. Primary Mathematics Standards Edition Grade 6

52. Primary Mathematics Standards Edition Grade 6

53. How to make sure the butterfly cannot flyHow do you get a butterfly?First there is the egg which hatches into a caterpillar. The caterpillar eats and grows. At the right time, it makes a cocoon out of its own body. While in the cocoon, the caterpillar changes into a butterfly.When the butterfly is ready, it starts to break through the cocoon. First a hole appears. Then the butterfly struggles to come out through the hole. This can take a few hours.If you try to "help" the butterfly by cutting the cocoon, the butterfly will come out easily but it will never fly. Your "help" has destroyed the butterfly.The butterfly can fly because it has to struggle to come out. The pushing forces lots of enzymes from the body to the wing tips. This strengthens the muscles, and reduces the body weight. In this way, the butterfly will be able to fly the moment it comes out of the cocoon. Otherwise it will simply fall to the ground, crawl around with a swollen body and shrunken wings, and soon die.If the butterfly is not left to struggle to come out of the cocoon, it will never fly.We can learn an important lesson from the butterfly.Lim Siong GuanHead, Civil Service

54. How to make sure the butterfly cannot flyHow do you get a butterfly?First there is the egg which hatches into a caterpillar. The caterpillar eats and grows. At the right time, it makes a cocoon out of its own body. While in the cocoon, the caterpillar changes into a butterfly.When the butterfly is ready, it starts to break through the cocoon. First a hole appears. Then the butterfly struggles to come out through the hole. This can take a few hours.If you try to "help" the butterfly by cutting the cocoon, the butterfly will come out easily but it will never fly. Your "help" has destroyed the butterfly.The butterfly can fly because it has to struggle to come out. The pushing forces lots of enzymes from the body to the wing tips. This strengthens the muscles, and reduces the body weight. In this way, the butterfly will be able to fly the moment it comes out of the cocoon. Otherwise it will simply fall to the ground, crawl around with a swollen body and shrunken wings, and soon die.If the butterfly is not left to struggle to come out of the cocoon, it will never fly.We can learn an important lesson from the butterfly.Lim Siong GuanHead, Civil Service

55. Part 6The ability to monitor thinking as students read – metacognition as well as the ability to show working – communication are the other important competencies.

56. Challenging MCQsfor problems that are difficult for students to communicate solution methods

57. Ann, Beng and Siti each had some money at first. Ann gave Beng $0.50. Beng then gave Siti $0.75. Siti spent $0.25 on a ruler. At the end, they had $3 each. What is the difference between the amount of money that Ann and Siti had at first?$1.00$0.50$0.75$1.25Ann $3$3.50Beng $3$3.75$3.25Siti $3$3.25$2.50

58. Part 7This section explains the importance of number sense and the role of mental computations in developing number sense.

59. “Although students should become competent in the various mathematical skills, over-emphasising procedural skills without understanding the underlying mathematical principles should be avoided.”Ministry of Education 2006

60. Find the value of 12.2 ÷ 4 .Example 5

61. Find the value of 6005 – 1947 .Example 5

62. Find the value of99 + 9756 ÷ 8Find the value of200 – 53 9 x 9Find the value of73 – 15 42 ÷ 7Find the value of169 + 348 x 7

63. Basic Skillsmental computation is an important part of the curriculum

64. Basic Skillsmental strategies strengthen visualization ability

65. Part 8This section explains the role of the calculator – it is just a computing device. Thinking is still what students need to do.

66. Cup cakes are sold at 40 cents each. What is the greatest number of cup cakes that can be bought with $95? $95 ÷ 40 cents = 237.5Answer: 237 cupcakesBasic Skill Item

67. Basic Application Item

68. Part 9This section summarizes the five key competencies in mathematics.

69. Five Key CompetenciesVisualizationNumber SenseMetacognitionCommunicationPatterns – this is shown on the next slide

71. Part 10Must one knows a formula to calculate the area of a trapezium.

72. 9 cm26 cm2With visualization, one does not need to know a formula to calculate the area of a trapezium.