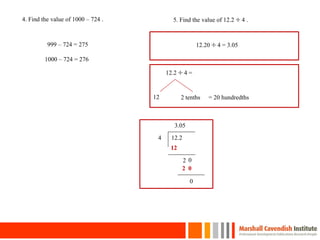
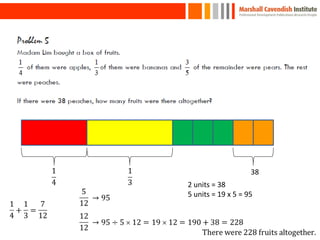
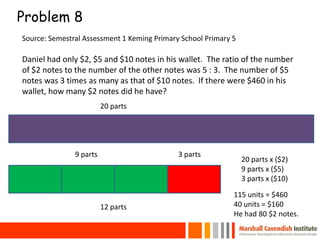
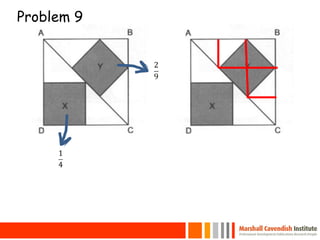
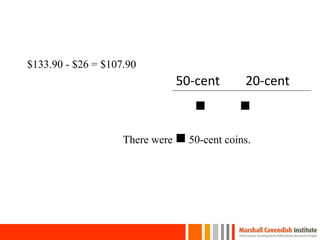
This document provides an overview of a presentation on helping children with primary mathematics. It discusses how mathematics can develop intellectual competence and reflects on shifts in test questions to require more conceptual understanding and real-world problem solving over rote algorithms. Examples of math questions and lessons from various primary grades in Singapore, the US, UK, Netherlands and Japan are presented, covering topics like number sense, patterns, problem solving and visual models. Key competencies and strategies for problem solving are discussed.

1. PEM 121
Helping Children with Primary Mathematics
with a focus on Primary 4 – 6
Dr Yeap Ban Har
Marshall Cavendish Institute
Singapore
banhar@sg.marshallcavendish.com
Slides are available at www.facebook.com/MCISingapore
Da Qiao Primary School, Singapore

2. Mathematics is “an excellent vehicle for the
development and improvement of a person’s
intellectual competence”.
Ministry of Education, Singapore (2006)
thinkingschools
learningnation

3. Ministry of Education, Singapore (1991, 2000, 2006, 2012)

5. Reflection of the Shifts in the Test Questions
When we compare the tests from the past with the present, we see that:
• Questions from previous tests were simpler, one or two steps, or were heavily scaffolded. The new
questions will requires multiple steps involving the interpretation of operations.
• Questions from the past were heavy on pure fluency in isolation. The new questions require conceptual
understanding and fluency in order to complete test questions.
• Questions from past tests isolated the math. The new problems are in a real world problem context.
• Questions of old relied more on the rote use of a standard algorithm for finding answers to problems.
The new questions require students to do things like decompose numbers and/or shapes, apply
properties of numbers, and with the information given in the problem reach an answer. Relying solely
on algorithms will not be sufficient.
Department of Education
New York State (2013)
5

6. What is Happening
Around the World?Bringing Up Children Who Are Ready for the Global, Technological World

7. Da Qiao Primary School, Singapore
17 – 3 = 
17 – 8 = 
Primary 1 Singapore
7

8. Da Qiao Primary School, Singapore
Primary 1 Singapore
8
Learning by Doing
Learning by Interacting
Learning by Exploring
Gardner’s Theory of
Intelligences
Bruner’s Theory of
Representations
Dienes’ Theory of Learning
Stages

9. St Edward School, Florida
Grade 2 USA
9

10. St Edward School, Florida


 
Grade 2 USA
10

11. Archipelschool De Tweemaster – Kameleon,
The Netherlands
Grade 5 The Netherlands
11

12. Archipelschool De Tweemaster – Kameleon,
The Netherlands
Grade 5 The Netherlands
12

13. Archipelschool De Tweemaster – Kameleon,
The Netherlands
Grade 5 The Netherlands
13

14. mathematics
14
Students in Advanced Benchmark can
• apply their understanding and knowledge in a
variety of relatively complex situations
• and explain their reasoning.

15. King Solomon Academy, London
Year 7 England
15

16. 16
The sum of the two numbers is 88.
The greater number is 6 x (88  11) = 48.
The other number is 5 x (88  11) = 40.

17. High School Attached to Tsukuba University, Japan
Draw a polygon with no
dots inside it.
Investigate.
A polygon has 4 dots on
the perimeter. Find an
expression for its area.
Grade 9 Japan
17

18. What Do Children
Learn in School
Mathematics?
And How You Can Coach Them

19. Students who have mastered the basic skills which include basic
one-step and two-step problems are ready to handle at least the
least demanding of the secondary courses.
Jay
Sam
34.7 kg
34.7 kg x 2 = (68 + 1.4) kg
34.7 kg x 2 = 69.4 kgSam’s mass is 69.4 kg.
19

20. 4. Find the value of 1000 – 724 . 5. Find the value of 12.2  4 .
20
999 – 724 = 275
1000 – 724 = 276
12.20  4 = 3.05
12.2  4 =
12 2 tenths = 20 hundredths
12.24
12
2 0
2 0
0
3.05

21. What Are the
Challenging
Aspects of
Mathematics?
And How Children Develop Competencies to Handle Them

22. Problem 1
Mr Lim packed 940 books equally into 8 boxes. What was
the least number of additional books he would need so that
all the boxes contained the same number of books?
Answer:__________
22
940  8 = 117.5
4
118 × 8 = 944

23. Problem 1
Cup cakes are sold at 40 cents each.
What is the greatest number of cup cakes that can be bought
with $95?

Answer:_____________
23
$95  40 cents = 237.5
237



24. Problem 1
Cup cakes are sold at 40 cents each.
What is the greatest number of cup cakes that can be bought
with $95?

Answer:_____________
24
237 

25. Problem 2
Mr Tan rented a car for 3 days. He was charged $155 per
day and 60 cents for every km that he travelled. He paid
$767.40. What was the total distance that he travelled for
the 3 days?
25
$155 x 3 = $465
$767.40 - $465 = $302.40
$302.40  60 cents / km = 504 km
He travelled 504 km.

26. Problem 2
Mr Tan rented a car for 3 days. He was charged $155 per
day and 60 cents for every km that he travelled. He paid
$767.40. What was the total distance that he travelled for
the 3 days?
26
(767.40 - 155 x 3)  0.60 = 504
He travelled 504 km.



27. 27
(25 + 2)  3 = 9
9 + 1 = 10
10 x 8 + 25 = 105
105

28. 28
11m + 6 = 8(m + 1) + 25
3m = 27
m = 9
10511m + 6 = 99 + 6 = 105

29. 29
Number of Girls 11 sweets 8 sweets
105
2 11 + 6 16 + 25
3 22 + 6 24 + 25
4 33 + 6 32 + 25

30. 30
men
women
There were 4 x 30 = 120 men and women at first.
After

31. 31
2 fifths of the remainder were 38
3 fifths of the remainder were 19 x 3 = …
There were 19 x 5 pears and peaches.
5 twelfths of the fruits = 19 x 5 fruits
So, there were 19 x 12 fruits altogether.
Answer: 228 fruits

32. 38
2 units = 38
5 units = 19 x 5 = 95
32

33. 33
0 + 1 + 2 + 3 = 2 x 3 = 6
6 x $3 = $18
$100 - $18 = $82
$82 : 4 = $20.50
$20.50 + $9 = $29.50

34. • Number Sense
• Patterns
• Visualization
• Communication
• Metacognition
Five Core Competencies
 Try to do as you read the problems. Do not wait till the end of the question to try to
do something.
 Try to draw when you do not get what the question is getting at. Diagrams such as
models are very useful.
 Do more mental computation when practising Paper 1.

35. Problem 7
35
Source: Semestral Assessment 1 River Valley Primary School Primary 4
Ravi had 12 more marbles than Jim at first. Then Jim gave Ravi 4 marbles.
How many more marbles does Ravi have than Jim in the end?
12Ravi
Jim 4
4

36. Problem 8
36
Source: Semestral Assessment 1 Keming Primary School Primary 5
Daniel had only $2, $5 and $10 notes in his wallet. The ratio of the number
of $2 notes to the number of the other notes was 5 : 3. The number of $5
notes was 3 times as many as that of $10 notes. If there were $460 in his
wallet, how many $2 notes did he have?
12 parts
20 parts
9 parts 3 parts
20 parts x ($2)
9 parts x ($5)
3 parts x ($10)
115 units = $460
40 units = $160
He had 80 $2 notes.

37. Problem 9
37

38. (a) 41 is under M
(b) 101 is under S
(c) 2011 is under T …. Really? How do you know?
Problem 10

39. Problem 11
Weiyang started a savings plan by putting 2 coins in a money
box every day. Each coin was either a 20-cent or 50-cent coin.
His mother also puts in a $1 coin in the box every 7 days. The
total value of the coins after 182 days was $133.90.
(a) How many coins were there altogether?
(b) How many of the coins were 50-cent coins?
182  7 = …
2 x 182 + 26 = …

40. $133.90 - $26 = $107.90
There were  50-cent coins.
50-cent 20-cent
 

41. Suppose each day he put in one 20-cent and one 50-cent coins,
the total is $127.40
But he only put in $107.90 ..
to reduce this by $19.50, exchange 50-cent for 20-cent coins
$19.50  $0.30 = 65
There were 182 – 65 = 117 fifty-cent coins.