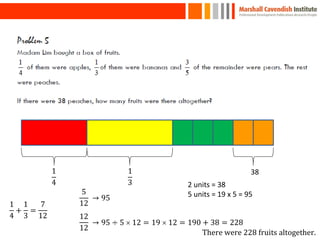
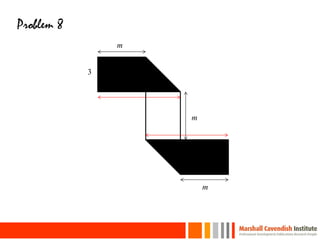
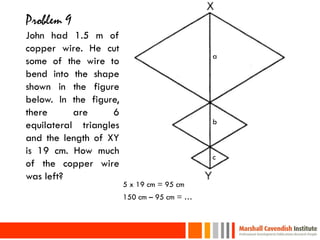
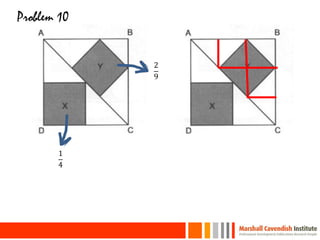
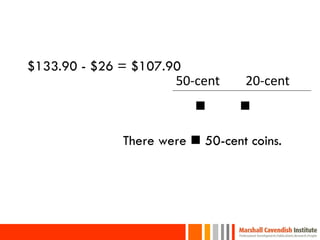
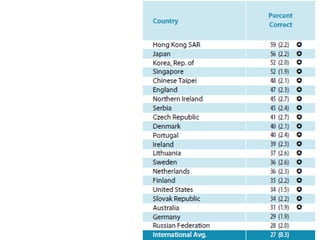
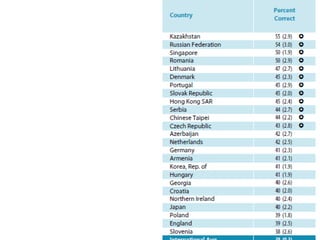
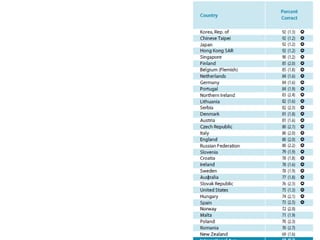
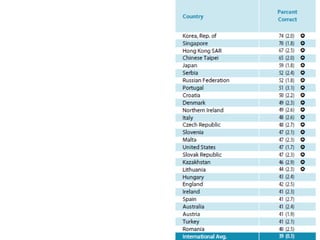
This document provides a summary of a presentation on surviving math given by Dr. Yeap Ban Har from the Marshall Cavendish Institute in Singapore. The presentation included slides available on Facebook and discussed shifts in math test questions over time towards requiring more conceptual understanding. It also showed sample math problems and performance data from Primary 4 students in Singapore on TIMSS tests. The document lists the speaker, location, contact information and source of additional slides.

1. Surviving Math! 3
presented by Gold 90.5 FM
Dr Yeap Ban Har
Marshall Cavendish Institute
Singapore
Da Qiao Primary School, Singapore
banhar@sg.marshallcavendish.com
Slides are available at www.facebook.com/MCISingapore

2. thinkingschools
learningnation
Mathematics is “an excellent vehicle for
the development and improvement of a
person’s intellectual competence”.
Ministry of Education, Singapore (2006)

3. Ministry of Education, Singapore (1991, 2000, 2006, 2012)

5. Reflection of the Shifts in the Test Questions
When we compare the tests from the past with the present, we see that:
• Questions from previous tests were simpler, one or two steps, or were heavily
scaffolded. The new questions will requires multiple steps involving the
interpretation of operations.
• Questions from the past were heavy on pure fluency in isolation. The new questions
require conceptual understanding and fluency in order to complete test questions.
• Questions from past tests isolated the math. The new problems are in a real world
problem context.
• Questions of old relied more on the rote use of a standard algorithm for finding
answers to problems. The new questions require students to do things like decompose
numbers and/or shapes, apply properties of numbers, and with the information
given in the problem reach an answer. Relying solely on algorithms will not be
sufficient.
Department of Education
New York State (2013)
5

6. What is Happening Around
the World?
Bringing Up Children Who Are Ready for the Global, Technological World

7. 7
Primary 1 Singapore
17 – 3 = 
17 – 8 = 
Da Qiao Primary School, Singapore

8. 8
Primary 1 Singapore
Learning by Doing
Learning by Interacting
Learning by Exploring
Gardner’s Theory of
Intelligences
Bruner’s Theory of
Representations
Dienes’ Theory of Learning
Stages
Da Qiao Primary School, Singapore

9. 9
Grade 2 USA
St Edward School, Florida

10. 10
Grade 2 USA


St Edward School, Florida
 

11. 11
Grade 5 The Netherlands
Archipelschool De Tweemaster – Kameleon,
The Netherlands

12. 12
Grade 5 The Netherlands
Archipelschool De Tweemaster – Kameleon,
The Netherlands

13. 13
Grade 5 The Netherlands
Archipelschool De Tweemaster – Kameleon,
The Netherlands

14. mathematics
Students in Advanced Benchmark can
• apply their understanding and
knowledge in a variety of relatively
complex situations
• and explain their reasoning.
14

15. 15
King Solomon Academy, London
Year 7 England

16. 16
The sum of the two numbers is 88.
The greater number is 6 x (88  11) = 48.
The other number is 5 x (88  11) = 40.

17. High School Attached to Tsukuba University, Japan
Draw a polygon with no
dots inside it.
Investigate.
Grade 9 Japan
A polygon has 4 dots on
the perimeter. Find an
expression for its area.
17

18. What Do Children Learn in
School Mathematics?
And How You Can Coach Them

19. Students who have mastered the basic skills which include basic
one-step and two-step problems are ready to handle at least the
least demanding of the secondary courses.
Jay 34.7 kg
Sam 34.7 kg x 2 = (68 + 1.4) kg
Sam’s mass is 69.4 kg. 34.7 kg x 2 = 69.4 kg
19

20. 4. Find the value of 1000 – 724 . 5. Find the value of 12.2  4 .
999 – 724 = 275 12.20  4 = 3.05
1000 – 724 = 276
12.2  4 =
12 2 tenths = 20 hundredths
3.05
4 12.2
12
20
20
0
20

21. What Are the Challenging
Aspects of Mathematics?
And How Children Develop Competencies to Handle Them

22. Problem 1
Cup cakes are sold at 40 cents each.
What is the greatest number of cup cakes that
can be bought with $95?
 $95  40 cents = 237.5
 237 
Answer:_____________
22

23. Problem 1
Cup cakes are sold at 40 cents each.
What is the greatest number of cup cakes that
can be bought with $95?
 237 
Answer:_____________
23

24. Problem 2
Mr Tan rented a car for 3 days. He was
charged $155 per day and 60 cents for
every km that he travelled. He paid
$767.40. What was the total distance that
he travelled for the 3 days?
$155 x 3 = $465
$767.40 - $465 = $302.40
$302.40  60 cents / km = 504 km
He travelled 504 km.
24

25. Problem 2
Mr Tan rented a car for 3 days. He was
charged $155 per day and 60 cents for
every km that he travelled. He paid
$767.40. What was the total distance that
he travelled for the 3 days?
 (767.40 - 155 x 3)  0.60 = 504
 He travelled 504 km.
25

26. (25 + 2)  3 = 9
9 + 1 = 10
10 x 8 + 25 = 105
105
26

27. 11m + 6 = 8(m + 1) + 25
3m = 27
m=9
11m + 6 = 99 + 6 = 105 105
27

28. Number of Girls 11 sweets 6 sweets
2 11 + 6 12 + 25
3 22 + 6 18 + 25
4 33 + 6 24 + 25
105
28

29. After
men
women
There were 4 x 30 = 120 men and women at first.
29

30. 2 fifths of the remainder were 38
3 fifths of the remainder were 19 x 3 = …
There were 19 x 5 pears and peaches.
1 1 So, there were 19 x 12 fruits altogether.
1− − = …
4 3
5 twelfths of the fruits = 19 x 5 fruits Answer: 228 fruits
30

31. 31
1 1 38
4 3 2 units = 38
5 5 units = 19 x 5 = 95
→ 95
1 1 7 12
+ =
4 3 12 12
→ 95 ÷ 5  12 = 19  12 = 190 + 38 = 228
12
There were 228 fruits altogether.

32. 0+1+2+3=2x3=6
6 x $3 = $18
$100 - $18 = $82
$82 : 4 = $20.50
$20.50 + $9 = $29.50
32

33. C
A
Problem 7
Mr Lim packed 387 apples. B
Each apple had a mass of about 24g.
He put them into three different baskets.
The mass of the apples in Basket A was 3 times that of the apples in Basket C.
The mass of the apples in Basket B is twice that of the apples in Basket C.
The mass of the empty Basket C was 140g.
What was the total mass of Basket C and the apples in it?
Source: Sent by a Parent to Gold 90.5FM
The total mass of the apples is about 387 x 24g = 9 288g
6 units = 9 288 g
1 units = 1 548 g
Basket C : 140 g + 1 548 g = 1 688 g = 1.688 kg
33

34. Problem 8
m
3
m
m
34

35. Problem 9
John had 1.5 m of
copper wire. He cut
a
some of the wire to
bend into the shape
shown in the figure
below. In the figure,
there are 6
b
equilateral triangles
and the length of XY
is 19 cm. How much
c
of the copper wire
was left?
5 x 19 cm = 95 cm
150 cm – 95 cm = …
35

36. Problem 10
2
9
1
4
36

37. Problem 11
(a) 41 is under M
(b) 101 is under S
(c) 2011 is under T …. Really? How do you know?

38. Problem 12
Weiyang started a savings plan by putting 2
coins in a money box every day. Each coin was
either a 20-cent or 50-cent coin. His mother also
puts in a $1 coin in the box every 7 days. The
total value of the coins after 182 days was
$133.90.
(a) How many coins were there altogether?
(b) How many of the coins were 50-cent coins?
182  7 = …
2 x 182 + 26 = …

39. $133.90 - $26 = $107.90
50-cent 20-cent
 
There were  50-cent coins.

40. Suppose each day he put in one 20-cent and one
50-cent coins, the total is $127.40
But he only put in $107.90 ..
to reduce this by $19.50, exchange 50-cent for
20-cent coins
$19.50  $0.30 = 65
There were 182 – 65 = 117 fifty-cent coins.

41. Five Core Competencies
• Number Sense
• Patterns
• Visualization
• Communication
• Metacognition
 Try to do as you read the problems. Do not wait till the end of the question to try
to do something.
 Try to draw when you do not get what the question is getting at. Diagrams such as
models are very useful.
 Do more mental computation when practising Paper 1.

42. Surviving Math! 3
presented by Gold 90.5 FM
Dr Yeap Ban Har
Marshall Cavendish Institute
Singapore
Da Qiao Primary School, Singapore
banhar@sg.marshallcavendish.com
Slides are available at www.facebook.com/MCISingapore

43. Surviving Math! 3
presented by Gold 90.5 FM
Dr Yeap Ban Har
Marshall Cavendish Institute
Singapore
Da Qiao Primary School, Singapore
Some Singapore data on how Primary 4 students performed on
some mathematics problems. This was the data for TIMSS2011.

44. Trends in International Mathematics
and Science Study TIMSS