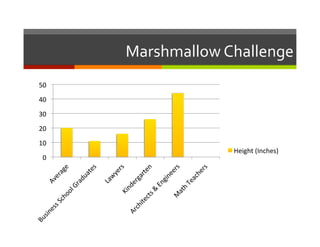
The document discusses strategies for engaging students in mathematics learning. It begins by outlining instructional objectives and classroom management techniques. It then describes activities teachers can use to actively involve students, such as the Marshmallow Challenge problem solving activity, Mix-N-Match pairing activity, Line-Ups ranking activity, and Inside-Outside Circle discussion format. The goal is to strategically use questioning, discussion, and hands-on challenges to maximize learning for all students.

1. ì
Engaging
Students
in
Learning
CPSB
High
School
Mathema2cs
Inservice,
2012

2. Organized
Chaos

3. COMPASS
« Se#ng
Instruc-onal
Outcomes
(1c):
Establishing
clear,
rigorous
objec2ves
that
describe
what
students
will
learn.
« Managing
Classroom
Procedures
(2c):
Establishing
a
smoothly
func2oning
classroom
through
the
management
of
instruc2on
and
transi2ons
to
allow
for
maximum
learning
for
all
students.
« Using
Ques-oning
and
Discussion
(3b):
Strategically
using
a
varied
set
of
ques2ons
to
engage
all
students
in
discussion
around
rigorous
content.
« Engaging
Students
in
Learning
(3c):
Asking
all
students
to
do
work
that
is
rigorous
an
intellectually
challenging.
« Using
Assessment
in
Instruc-on
(3d):
Using
clear
assessment
criteria
to
drive
instruc2onal
choices
throughout
the
lesson
and
at
the
end.

4. Standards
of
Mathematical
Practice
« Make
sense
of
problems
and
persevere
in
solving
them.
« Reason
abstractly
and
quan2ta2vely.
« Construct
viable
arguments
and
cri2que
the
reasoning
of
others.
« Model
with
mathema2cs.
« Use
appropriate
tools
strategically.
« ALend
to
precision.
« Look
for
and
make
use
of
structure.
« Look
for
and
express
regularity
in
repeated
reasoning.

5. Attention
Getter

6. Marshmallow
Challenge
« 20
s2cks
of
spagheN
« 1
yard
of
tape
« 1
yard
of
string
« 1
marshmallow

7. Marshmallow
Challenge
« The
winning
team
is
the
one
that
has
the
tallest
structure
measured
from
the
table
top
surface
to
the
top
of
the
marshmallow.
« The
en2re
marshmallow
must
be
on
top.
« Use
as
much
or
as
liLle
of
the
kit.
« Break
up
the
spagheN,
string,
or
tape.
« The
challenge
lasts
for
18
minutes.

8. Marshmallow
Challenge

9. Marshmallow
Challenge
50
40
30
20
10
Height
(Inches)
0

10. Marshmallow
Challenge

11. Marshmallow
Challenge
« Why
do
kindergarteners
create
taller
and
more
interes2ng
structures
than
business
graduates?
« The
marshmallow
is
a
metaphor
for
the
hidden
assump2ons
of
a
project.
« What
are
your
assump2ons
this
school
year?

12. Mix-­‐N-­‐Match
« Each
student
is
given
a
card
with
some
type
of
problem
or
informa2on
on
it.
« Students
‘mix’
and
find
the
person
with
a
card
that
‘matches’
theirs.
« As
students
pair
up,
they
move
to
the
outside
perimeter
of
the
classroom
and
stand
together
as
a
pair.
« Once
everyone
has
found
their
match,
students
confer
with
another
nearby
pair
to
double
check
that
they
do
indeed
make
a
match.
« Redistribute
if
desired.

13. Mix-­‐N-­‐Match
Name
the
property
In
simplest
radical
form,
find
the
demonstrated:
distance
between:
7! 9!5 = 7!9 !5
( ) ( ) (1, !3), ( 7, 2)
Simplify
(posi2ve
exponents):
Sketch
the
graph
of:
!3 2
6x y
( ) y = 2sin x
7
x
Find
the
remainder
when
Evaluate
the
determinant:
3
2 " 1 !4 %
3x + 2x
! 5x ! 2 $ '
is
divided
by
(
x
+
2
)
# 3 !2 &

14. Line-­‐Ups
« Each
student
is
given
a
card
with
some
type
of
problem
on
it.
« Students
evaluate
the
answer
to
their
problem
and
then
line
up
in
order
from
least
to
greatest.
« Once
students
are
lined
up,
they
then
discuss
their
card
and
posi2on
with
a
nearby
partner.
« Partners
may
be
formed
by
pairing
up
or
by
‘folding’
the
line
in
half.

15. Line-­‐Ups
« Line
up
in
order
from
the
teacher
who
has
taught
the
most
years
to
the
teacher
who
has
taught
the
fewest.
« Fold
the
line.
« The
more
experienced
teacher
tells
the
less
experienced
about
their
most
embarrassing
teaching
moment.
« The
less
experienced
teacher
then
shares
with
the
more
experienced
how
that
situa2on
could
have
been
avoided.

16. Line-­‐Ups
« Frac2ons,
Decimals,
&
Percents
« Sta2s2cs
« Order
of
Opera2ons
« Algebraic
Expressions
« Angle
Measures
« Radian
and
Degree
Measures
« Arithme2c
and
Geometric
Sequences

17. Inside-­‐Outside
Circle
« Students
form
two
concentric
circles,
with
equal
numbers
of
students
in
each
circle.
Students
stand
face-­‐to-­‐face
with
a
partner,
one
person
from
the
inside
circle
and
one
from
the
outside.
« The
circles
rotate
according
to
the
teacher’s
instruc2ons.
« Partners
take
turn
asking
each
other
ques2ons,
quizzing
each
other
with
flashcards,
sharing
some
informa2on,
or
answering
ques2ons.

18. Inside-­‐Outside
Circle
« Structure
works
best
when
the
problems
being
solved
do
not
require
lengthy
paper-­‐pencil
solu2ons.
« Structure
is
more
conducive
to
short-­‐answer
or
higher
level
thinking
ques2ons
that
can
be
answered
verbally.
« Any
ideas?

19. Rally
Coach
« Students
pair
up
and
decide
who
is
Person
A
and
who
is
Person
B.
There
is
only
one
sheet
of
paper
and
one
pencil
for
each
student
pair.
« Teacher
poses
a
problem,
verbally
or
on
paper.
« Person
A
begins
contribu2ng
to
the
solu2on
of
the
problem
in
wri2ng
and
states
aloud
what
(s)he
is
doing.
« Meanwhile,
Person
B
watches,
listens,
and
coaches.
If
necessary,
Person
B
reteaches.
« Reverse
roles.

20. Rally
Coach
« Mul2-­‐Step
problems
« Comple2ng
worksheets
« Genera2ng
lists
« Constructed
response
items

21. Round
Table
« Similar
to
Rally
Coach
but
involves
four
students
instead
of
two.
« Students
take
turns
passing
the
paper
and
pencil,
each
wri2ng
one
answer
or
making
a
contribu2on.

22. Round
Table
« Given
three
points,
A
(4,
-­‐7),
B
(3,
1),
and
C
(-­‐2,
0)…
« Person
1
finds
the
slope
of
the
line
passing
through
A
and
B.
« Person
2
writes
the
equa2on
of
line
AB.
« Person
3
writes
the
equa2on
of
the
line
parallel
to
AB
and
passing
through
C.
« Person
4
writes
the
equa2on
of
the
line
perpendicular
to
AB
and
passing
through
C.

23. Mix
Pair
Rally
Coach
« Each
student
is
given
a
card
containing
some
informa2on.
« Students
‘mix’
around
the
room
and
find
a
partner,
Person
A
and
Person
B.
« Person
A
solves
the
problem
on
his/her
card
while
Person
B
watches,
checks,
and
praises.
« Person
B
then
solve
the
problem
on
his/her
card
while
Person
A
watches,
checks,
and
praises.
« Partners
reteach
as
necessary.

24. Showdown
« Teacher
selects
one
student
from
each
group
to
be
the
Showdown
Captain.
« The
Showdown
Captain
draws
the
first
card,
reads
the
ques2on,
and
provides
think
2me.
« Working
alone,
all
students,
including
the
Showdown
Captain,
write
their
answers.
« ‘Showdown’
is
called
and
teammates
share
and
discuss
their
answers.

25. Showdown
« The
Showdown
Captain
leads
the
checking.
« If
correct,
the
team
celebrates;
if
not,
teammates
tutor,
then
celebrate.
« Repeat
with
a
new
captain.
« Modifica2ons—oral
ques2ons,
ques2ons
from
a
handout,
or
ques2ons
displayed
by
a
projector

26. Classroom
Setup

27. Stations
« Sta2on
1:
Students
will
be
given
eight
index
cards
with
func2ons
and
func2on
answers
on
them.
They
will
match
the
func2ons
with
the
appropriate
func2on
answers.
Then,
they
will
evaluate
func2ons.
« Sta2on
2:
Students
will
use
a
ruler
to
perform
the
ver2cal
line
test
on
graphs
of
rela2ons.
They
will
determine
if
the
rela2on
is
a
func2on.
They
will
construct
a
graph
that
is
a
func2on.
Then,
they
will
determine
if
a
rela2on
is
a
func2on
by
analyzing
coordinate
points.

28. Stations
« Sta2on
3:
Students
will
be
given
a
calculator
to
help
them
solve
a
real-­‐world
linear
func2on.
They
will
write
and
solve
a
linear
func2on
based
on
two
data
points.
« Sta2on
4:
Students
will
be
given
a
number
cube.
They
roll
the
number
cube
to
populate
a
rela2on.
They
find
the
domain
and
range
of
the
rela2on
and
determine
if
it
is
a
func2on.
Then
for
given
rela2ons,
they
determine
the
domain,
range,
and
whether
or
not
it
is
a
func2on.

29. Questions

30. References
« Kushnir,
Dina.
(2001).
Coopera*ve
learning
and
mathema*cs:
High
school
ac*vi*es.
San
Clemente,
CA:
Kagan
Publishing.
« The
Marshmallow
Challenge:
hLp://marshmallowchallenge.com