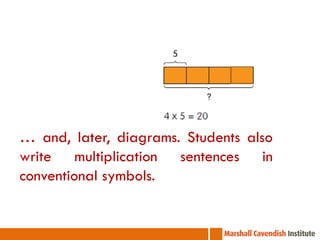
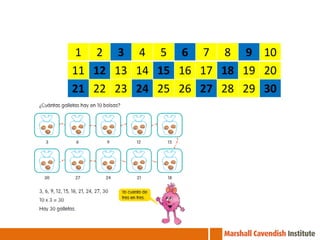
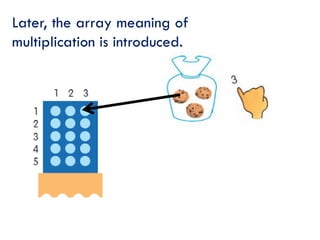
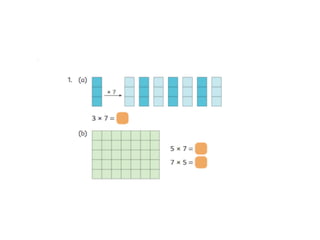
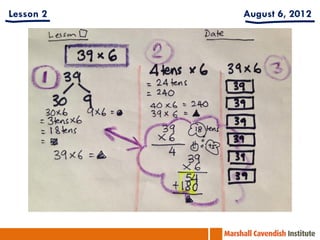
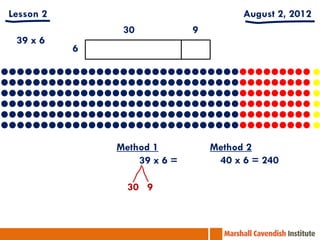
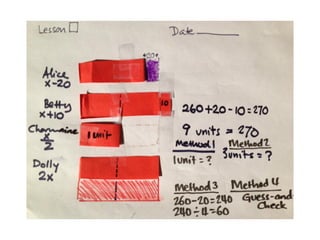
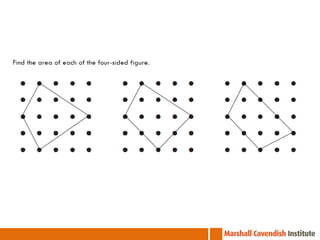
This document contains information from a presentation on Singapore Math given by Dr. Yeap Ban Har. It includes 6 lessons on various math topics taught using the Singapore Math approach such as multiplication, problem solving, bar modeling, and area of polygons. It emphasizes concepts like visualization, problem solving, conceptual understanding, and differentiated instruction. Contact and biography information is provided for Dr. Yeap Ban Har.

1. Dr. Yeap Ban Har
Marshall Cavendish Institute
Singapore
yeapbanhar@gmail.com
SINGAPORE
M AT H
Beyond the Basics
Day One
St Edward’s School
Slides are available at Florida, USA
www.banhar.blogspot.com
Marshall Cavendish Institute
www.facebook.com/MCISingapore www.mcinstitute.com.sg

2. Dr. Yeap Ban Har
CONTACT Marshall Cavendish Institute
INFO yeapbanhar@gmail.com
Slides are available at
www.banhar.blogspot.com Marshall Cavendish Institute
www.mcinstitute.com.sg
www.facebook.com/ MCISingapore

4. Introduction
We start the day with an overview of
Singapore Math.

6. Curriculum document is available at http://www.moe.gov.sg/

7. THINKING SCHOOLS
LEARNING NATION
Singapore Ministry of Education 1997

8. what
is singapore
mathematics

10. key focus
of singapore
mathematics

11. problem
solving

12. thinking

13. an
excellent
vehicle
for the development
&improvement of
a person’s intellectual
competencies
Ministry of Education Singapore 2006

14. conceptual
understanding

16. Fundamentals of Singapore Math – Review & Extend
 Thinking: It’s the Big Idea!
 Problem Solving, Visualization, Patterning, and
Number Sense
 The Concrete-Pictorial-Abstract Approach

17. Lesson 1
We do a case study on multiplication
facts. We will see the use of an anchor
task to engage students for an
extended period of time.

22. Strategy 1
Get 3 x 4 from 2 x 4
Strategy 2
Doubling
Strategy 3
Get 7 x 4 from 2 x 4 and 5 x 4
Strategy 4
Get 9 x 4 from 10 x 4

23. Strategy 1
Get 3 x 4 from 2 x 4

24. Strategy 3
Get 9 x 4 from 4 x 4 and 5 x 4
This is essentially the distributive
property. Do we introduce the
phrase at this point? Recall the
discussion on Dienes.

25. Strategy 2
Doubling

26. Strategy 4
Get 9 x 4 from 10 x 4

27. Unusual Response
Get 4 x 8 from 4 x 2. Can it be done? Does the number
of cups change? Does the number of counters per cup
change?

28. Differentiated Instruction
These are examples of how the lesson can be
differentiated for advanced learners.

29. Differentiated Instruction
These are examples of how the lesson can be
differentiated for advanced learners.

30. Exercise
Discuss the four ways to represent 1
group of 4. Which is used first? Why?
Which is used next? Why?

31. Textbook Study
Observe the various meanings of
multiplication from Grade 1 to Grade
3.

32. Prior to learning multiplication, students
learn to make equal groups using concrete
materials. Marbles is the suggested
materials.

33. After that they represent these concrete
situations using, first, drawings ..

34. Open Lesson in Chile

35. … and, later, diagrams. Students also
write multiplication sentences in
conventional symbols.

36. First, equal groups –
three groups of four. Third, four multiplied three
times ….
Second, array –
Three rows of four

37. Textbook Study
Observe how equal group
representation evolves into array and
area models. Also observe how the
multiplication tables of 3 and 6 are
related on the flights of stairs.

38. They begin with equal group representation.

39. 1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30

40. In Primary 2, students learn
multiplication facts of 2, 5, 10 and 3
and 4. In Primary 3, they learn the
multiplication facts of 6, 7, 8 and 9.

41. Later, the array meaning of
multiplication is introduced.

42. Square tiles are subsequently used to lead to
the area representation of multiplication.

46. Lesson 2
Multiplication of multi-digit numbers
taught in a problem-solving approach.

47. Lesson 2 August 6, 2012

48. Lesson 2 August 2, 2012
30 9
39 x 6
6
 
 
 
 
 
 
Method 1 Method 2
39 x 6 = 40 x 6 = 240
30 9

49. Lesson 3
Use digits 1 to 9 to make a correct
multiplication sentence =.

50. Open Lesson at Broomfield, Colorado

52. Students who were already good in the skill of multiplying two-digit number
with a single-digit number were asked to make observations. They were
asked “What do you notice? Are there some digits that cannot be used ta
all?”

53. Multiplication Around Us
Do you see multiplication in these work
of art around the venue of the
conference? Hilton Oak Lawn, IL

55. Lesson 4
We studied the strategies to help
struggling readers as well as those
weak in representing problem
situations.

56. Lesson 4 August 6, 2012

58. Lesson 5 August 2, 2012
In the end ... At first …
Alice 20
Betty 10
Charmaine
Dolly

59. Lesson 5
Question: How do we help students set up the model?
Students are introduced to the idea of using a
rectangle to represent quantities – known and
unknown. Paper strips are used. Later, only diagrams
are used. Advanced skills like cutting and moving are
learned in Grades 4, 5 and 6. How is the idea of
bar model introduced in Grades K – 3?
Lesson 5 shows a basic bar model solution in Grade
5.

60. Lesson 5 August 6, 2012
Carl
$4686
Ben

62. Differentiated instruction for
students who have difficulty
with standard algorithms. Use
number bonds.

64. 2x + x = 4686
3x = 4686
Students in Grade 7 may use algebra to deal with such situations. Bar model is
actual linear equations in pictorial form.

65. Lesson 6
Let’s look at the emphasis on visualization and
generalization in a task from a different topic –
area of polygons.

67. Differentiated Instruction
Is it true that the area of the quadrilateral is
half of the area of the square that ‘contains’ it?
Why is the third case different from the first
two? What are your ‘conjectures’?

68. It was observed that the area of the polygon is
half of the number of dots on the sides of the
polygon. Thus, the polygon on the left has 22
dots on the sides and an area of 11 square
units. Is this conjecture correct?

69. One of the participants used the
results to find the area of this
trapezoid. The red triangle has 3
dots on the sides (hence, area of
1.5 square units). The brown one
has 6 dots. The purple one has 6
dots, Hence, the area of these two
triangles is 3 square units each.

70. What
• Visualization
• Generalization
• Number Sense
How
• Tell
• Coach
• Model
• Provide
Opportunities
Tampines Primary School, Singapore