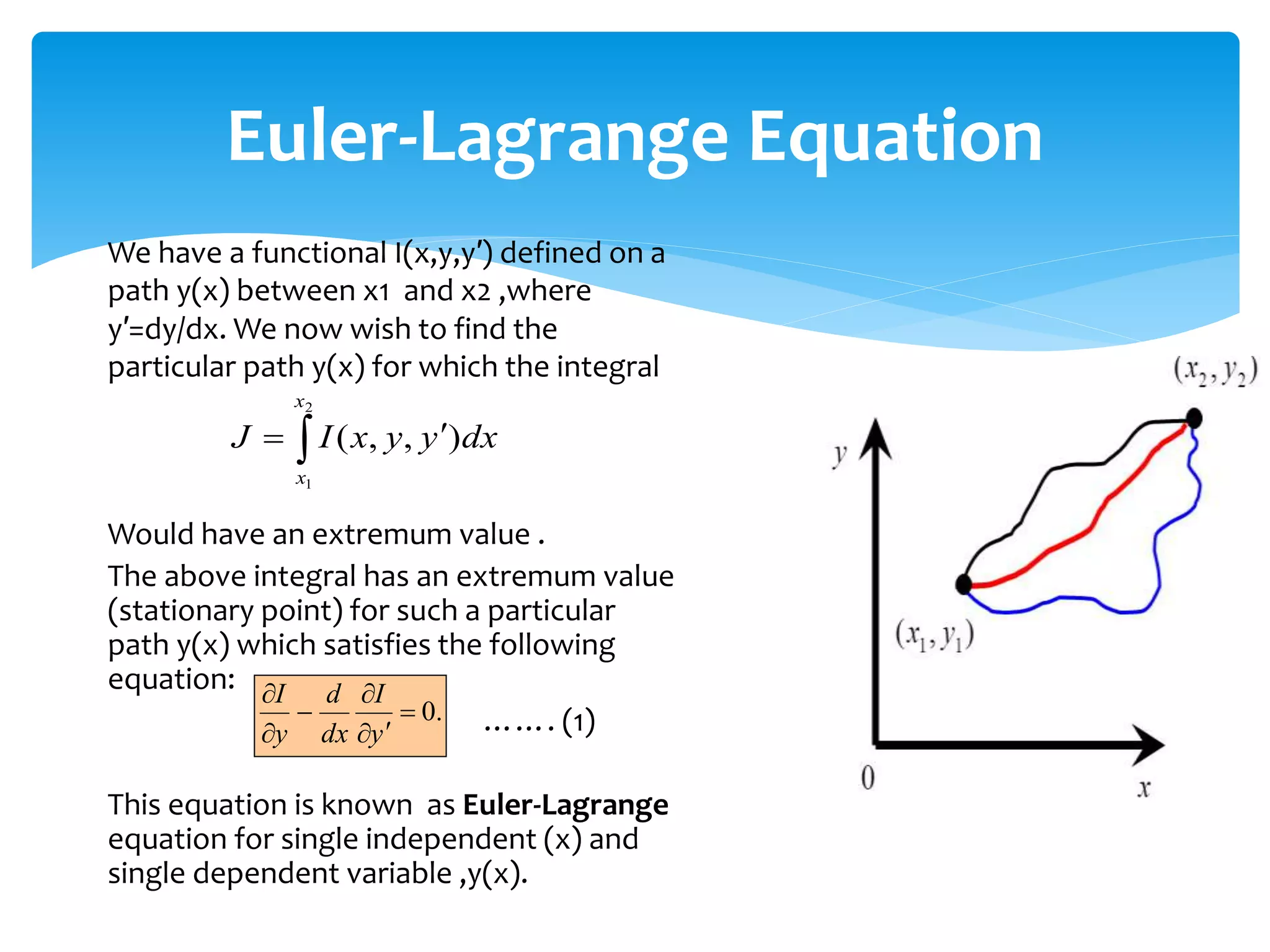
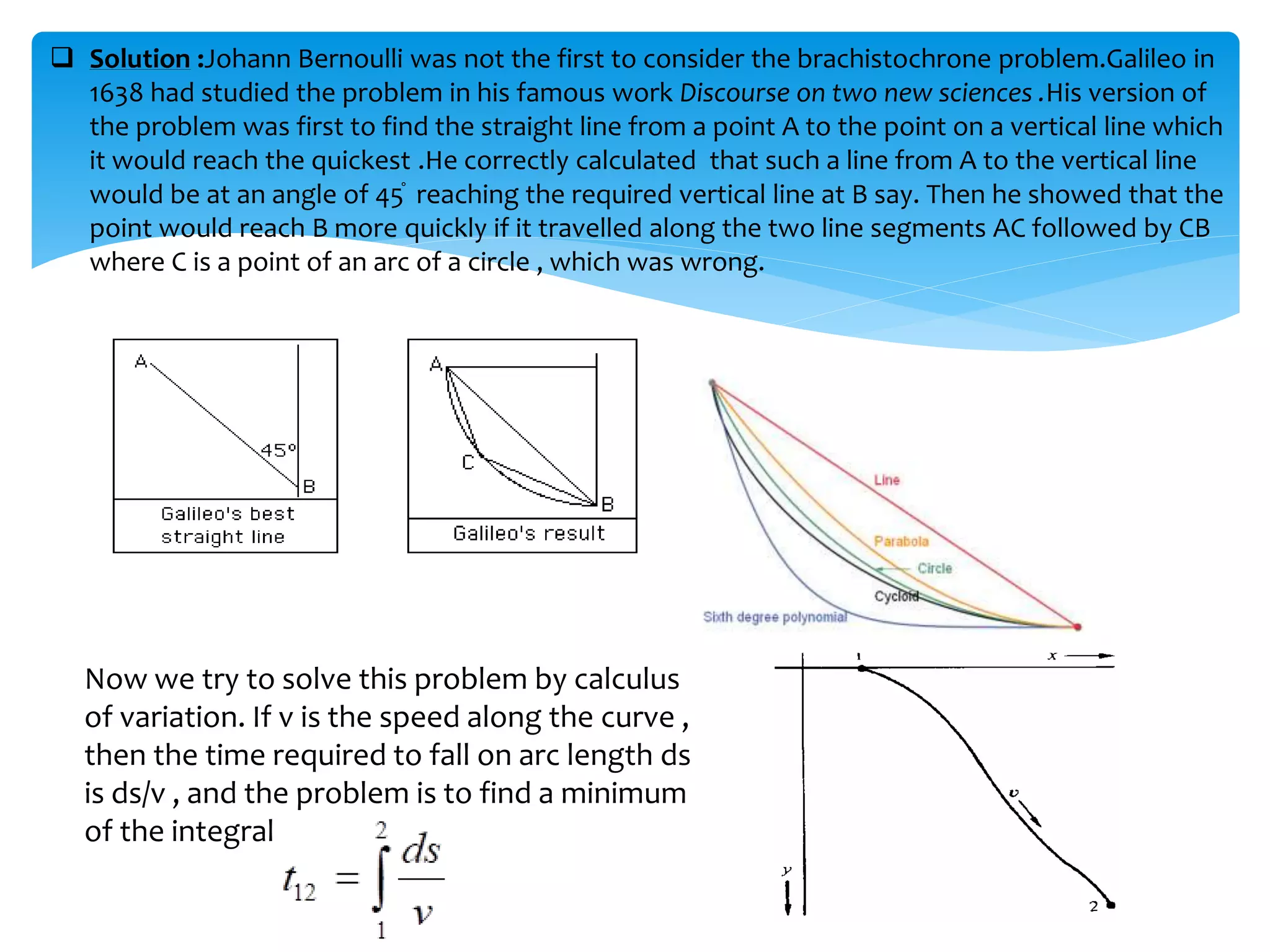
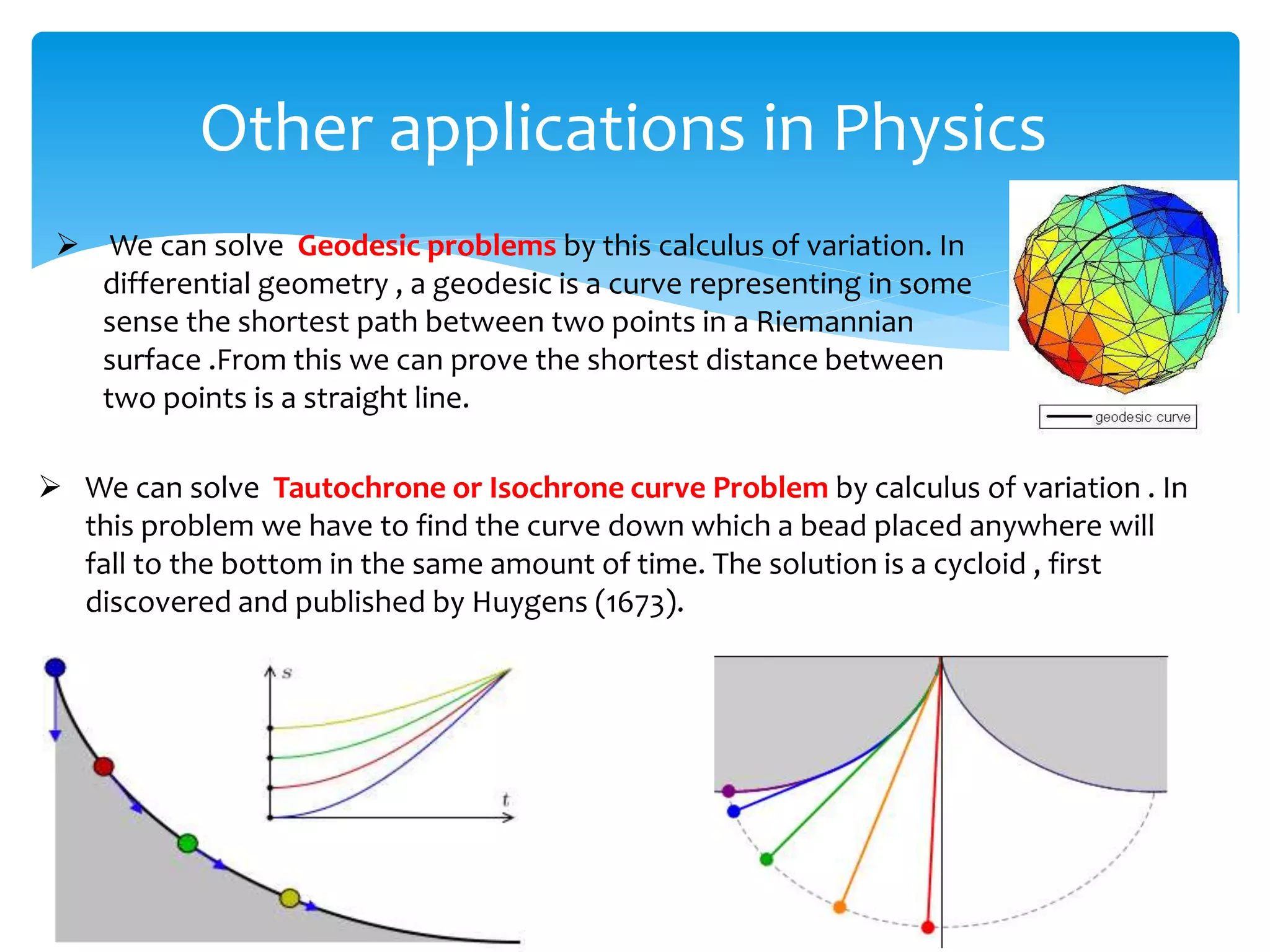
The document discusses the calculus of variation, including its history, key contributors, and fundamental concepts such as the Euler-Lagrange equation and the brachistochrone problem. It highlights various applications in physics, like geodesics and Hamilton's principle, while also outlining disadvantages of the method. Additionally, it includes references for further reading on the subject.

1. NAME:- SUBHAJIT PRAMANICK
ROLL:- MC/UG/S-V/19 NO:- 1224
REG. NO.:- 2017-1229
Topic:- Calculus of
variation
NAME:- SOUGATA DANDAPATHAK
ROLL:- MC/UG/S-V/19 NO:- 1225
REG. NO.:- 2017-1144
Submitted by:-

2.  What is Calculus of Variation?
 History
 Who develop calculus of variation?
 Euler-Lagrangian equation
 Brachistochrone Problem, The origin of
calculus of variation
 Other applications in Physics
 Disadvantages
 Reference
Contents

3. In differential calculus ,the necessary
condition for occurrence of a stationary value
of a funtion u(x) at x=a is u′(a)=0.Stationary
point of a function is that point in which the
change of function is zero, i.e., extremum
point (maxima or minima).It shall be
minimum or maximum depending u″(a)>0 or
u″(a)<0 respectively.
Similarly with the help of calculus of variation
we can determine stationary point of a
funtional. Basically funtionals are function of
function . Functionals are often expressed as
definite integrals of another functional
involving functions and their derivatives.
What is calculus of variation?

4. The calculus of variations may be said to begin with Newton’s
minimal resistance problem in 1687,followed by the
Brachistochrone curve problem raised by Johann Bernoulli (1696).
History

5. Who develop calculus of variation?
Johann Carl
Friedrich Gauss
(1777-1855)
Francois Antoine
de l’Hospital
(1661-1704)
Leonhard Euler
(1707-1783)
Augustin-Louis
Cauchy
(1789-1857)
Isaac Newton
(1642-1726)
Johann Bernoulli
(1667-1748)
Jacob Bernoulli
(1654-1705)
Gottfried Wilhelm
Von Leibniz
(1646-1716)

6. We have a functional I(x,y,y′) defined on a
path y(x) between x1 and x2 ,where
y′=dy/dx. We now wish to find the
particular path y(x) for which the integral
Would have an extremum value .
The above integral has an extremum value
(stationary point) for such a particular
path y(x) which satisfies the following
equation:
……. (1)
This equation is known as Euler-Lagrange
equation for single independent (x) and
single dependent variable ,y(x).
Euler-Lagrange Equation
 

2
1
)
,
,
(
x
x
dx
y
y
x
I
J
.
0







y
I
dx
d
y
I

7.  History : Brachistochrone Problem is the most famous problem in the
history of calculus of variation. Johann Bernoulli (1696) challenge this
problem to his brother Jacob Bernoulli .This problem became an open
challenge for all of mathematicians then. Newton solved this problem
just in 12 hours . But in the end , five mathematicians responded with
solutions: Newton, Jacob Bernoulli , Gottfried Leibniz, Ehrenfried
Walther Von Tschirnhaus and Guillaume de l’Hospital.
 Problem : Find a curve joining two points ,along which a
particle falling from rest under the influence of gravity
travels from the highest to the lowest points in the least
time.
Johann Bernoulli
(1667-1748)
Brachistochrone Problem, The origin of
Calculus of Variation

8.  Solution :Johann Bernoulli was not the first to consider the brachistochrone problem.Galileo in
1638 had studied the problem in his famous work Discourse on two new sciences .His version of
the problem was first to find the straight line from a point A to the point on a vertical line which
it would reach the quickest .He correctly calculated that such a line from A to the vertical line
would be at an angle of 45֯ reaching the required vertical line at B say. Then he showed that the
point would reach B more quickly if it travelled along the two line segments AC followed by CB
where C is a point of an arc of a circle , which was wrong.
Now we try to solve this problem by calculus
of variation. If v is the speed along the curve ,
then the time required to fall on arc length ds
is ds/v , and the problem is to find a minimum
of the integral

9. If y is measured down from the initial point of release,the conservation theorem for the
energy of the particle can be written as
i.e., v=√(2gy)
so, where,
Here I(x, y, y′= d y /dx)=
Using Euler-Lagrange equation we get the
parametric solution :


2
1
12
v
ds
t
 



2
1
2
2
/
1
dx
gy
dx
dy
mgy
mv

2
2
2
2
dy
dx
ds 

)
cos
1
(
)
sin
(







a
y
a
x
This is nothing but an equation of a cycloid.
So the particle moving along this cycloid
path takes least time. Forthis this cycloid is
also known as Brchistochrone curve.
Fig : The trajectory of a rest
particle on a moving cycle
ring , The Cycloid

10. Other applications in Physics
 We can solve Geodesic problems by this calculus of variation. In
differential geometry , a geodesic is a curve representing in some
sense the shortest path between two points in a Riemannian
surface .From this we can prove the shortest distance between
two points is a straight line.
 We can solve Tautochrone or Isochrone curve Problem by calculus of variation . In
this problem we have to find the curve down which a bead placed anywhere will
fall to the bottom in the same amount of time. The solution is a cycloid , first
discovered and published by Huygens (1673).

11.  Hamilton’s Principle is based on this Calculus of Variation.
According to this principle , the particle will move along that
path in which action is least. Sometimes it is called “The
Principle of Least Action” .
 Calculus of variation helps to solve The Isoperimetric
Problem . The Isoperimetric problem is to determine a
plane figure of the largest possible area whose boundary
has a specified length.
 Variational calculus is used in Einstein’s theory of General
Relativity . The most commonly used tools are lagrangians
and Hamiltonians which are used to derive the Einstein’s
Field equations .

12. Disadvantages
• Method gives extremals, but doesn’t indicate maximum or minimum
• Distinguishing mathematically between max/min is more difficult
• Usually have to use geometry of physical setup
• Solution curve y must have continuous second-order derivatives
• Requirement from integration by parts
• We are finding stationary states, which vary only in space, not in time
• Very few cases in which systems varying in time can be solved
• Even problems involving time (e.g. brachistochrones) don’t change in time

13. “Classical Mechanics” Herbert Goldstein
“Theoretical Mechanics” Murray R. Spiegel
 Google , Wikipedia,YouTube
Reference

14. THANK
YOU