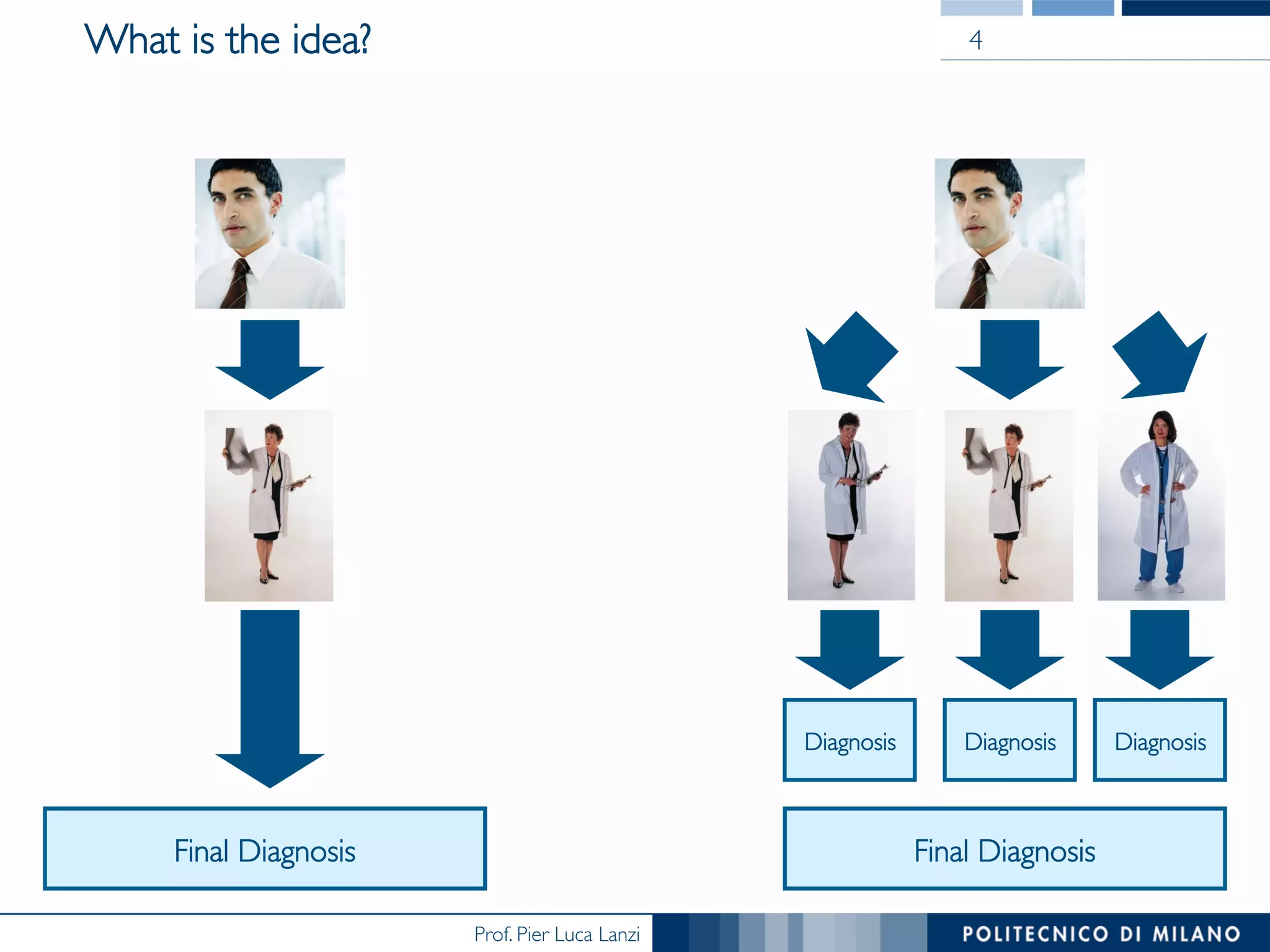
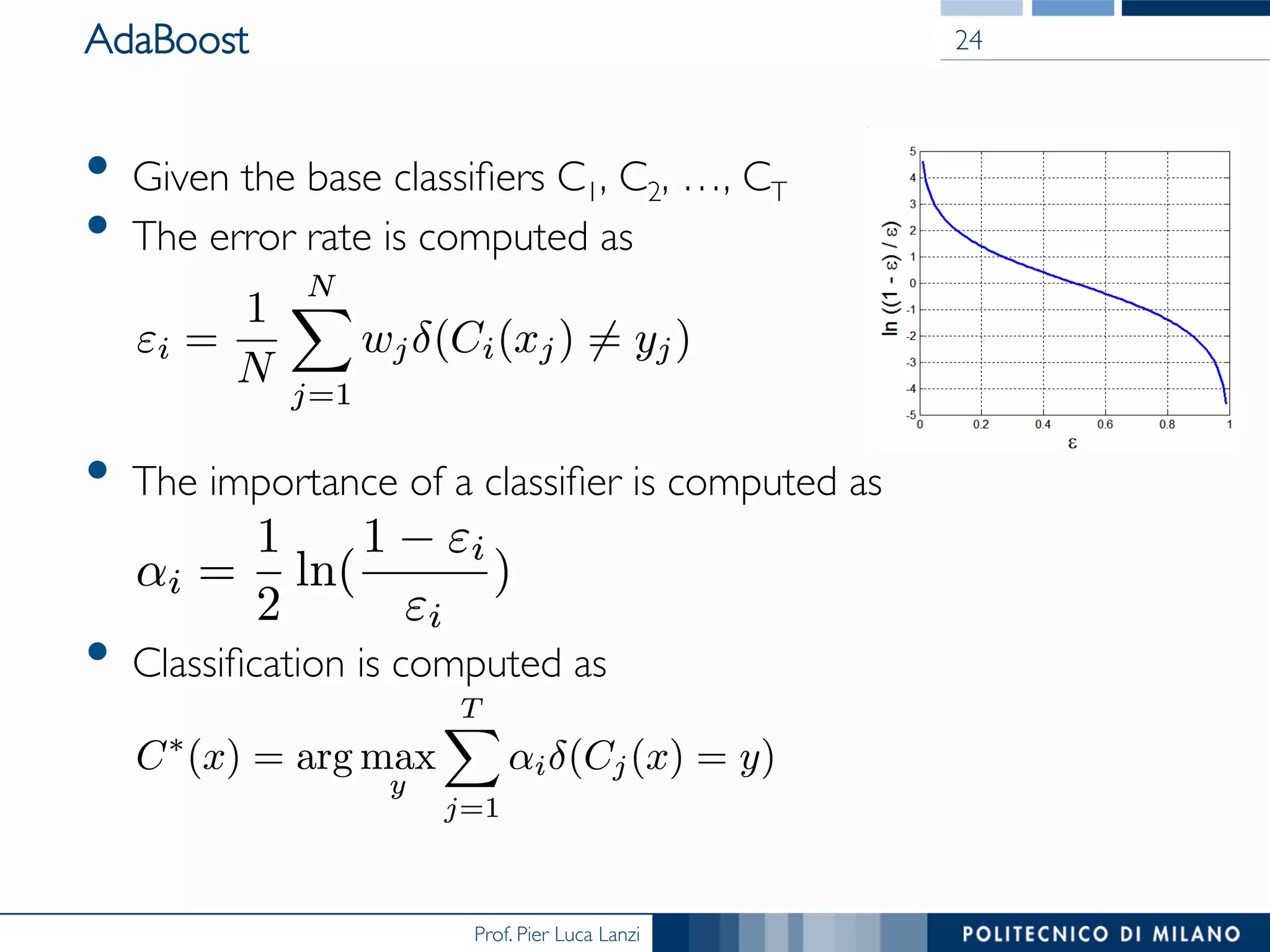
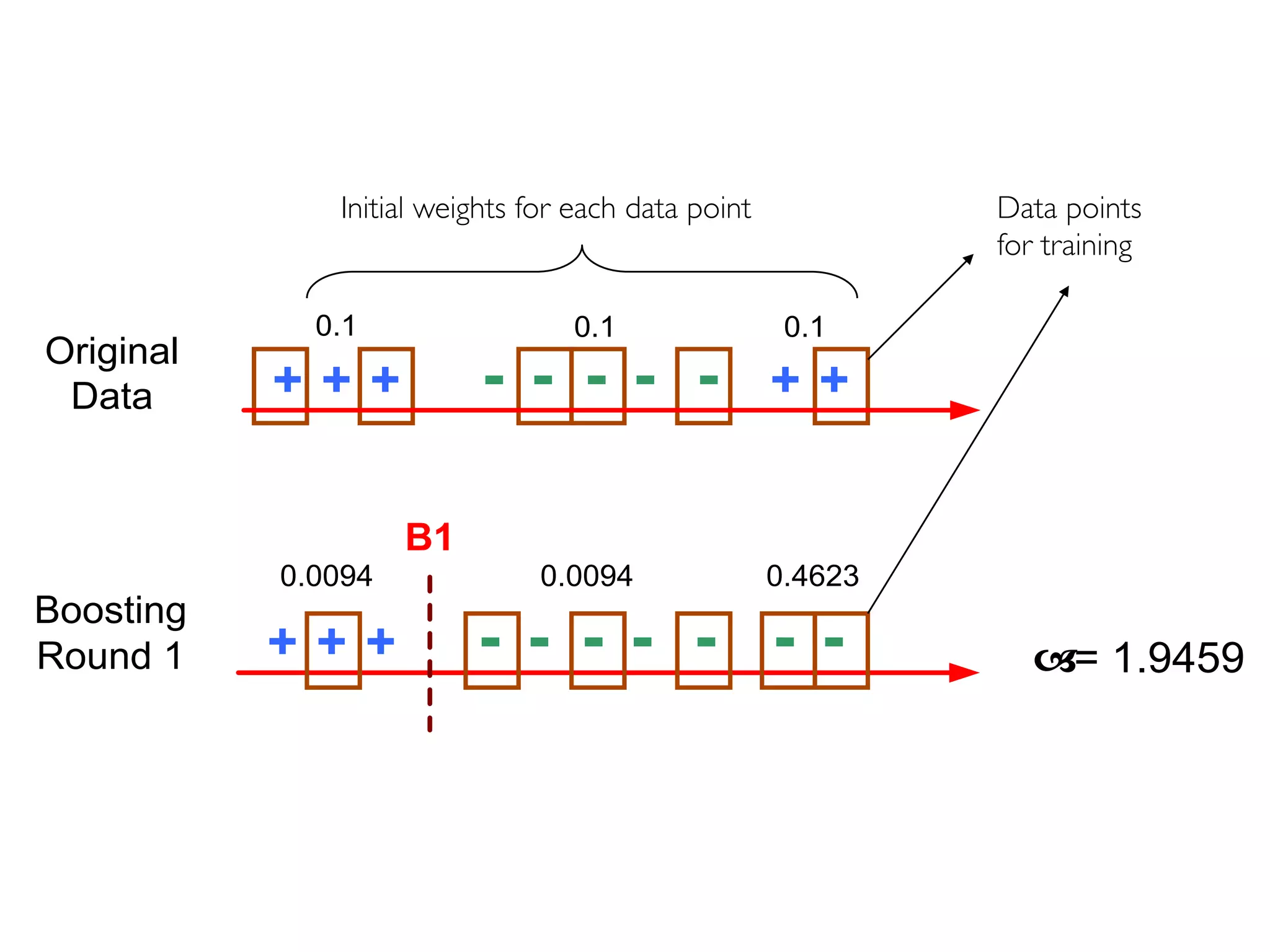
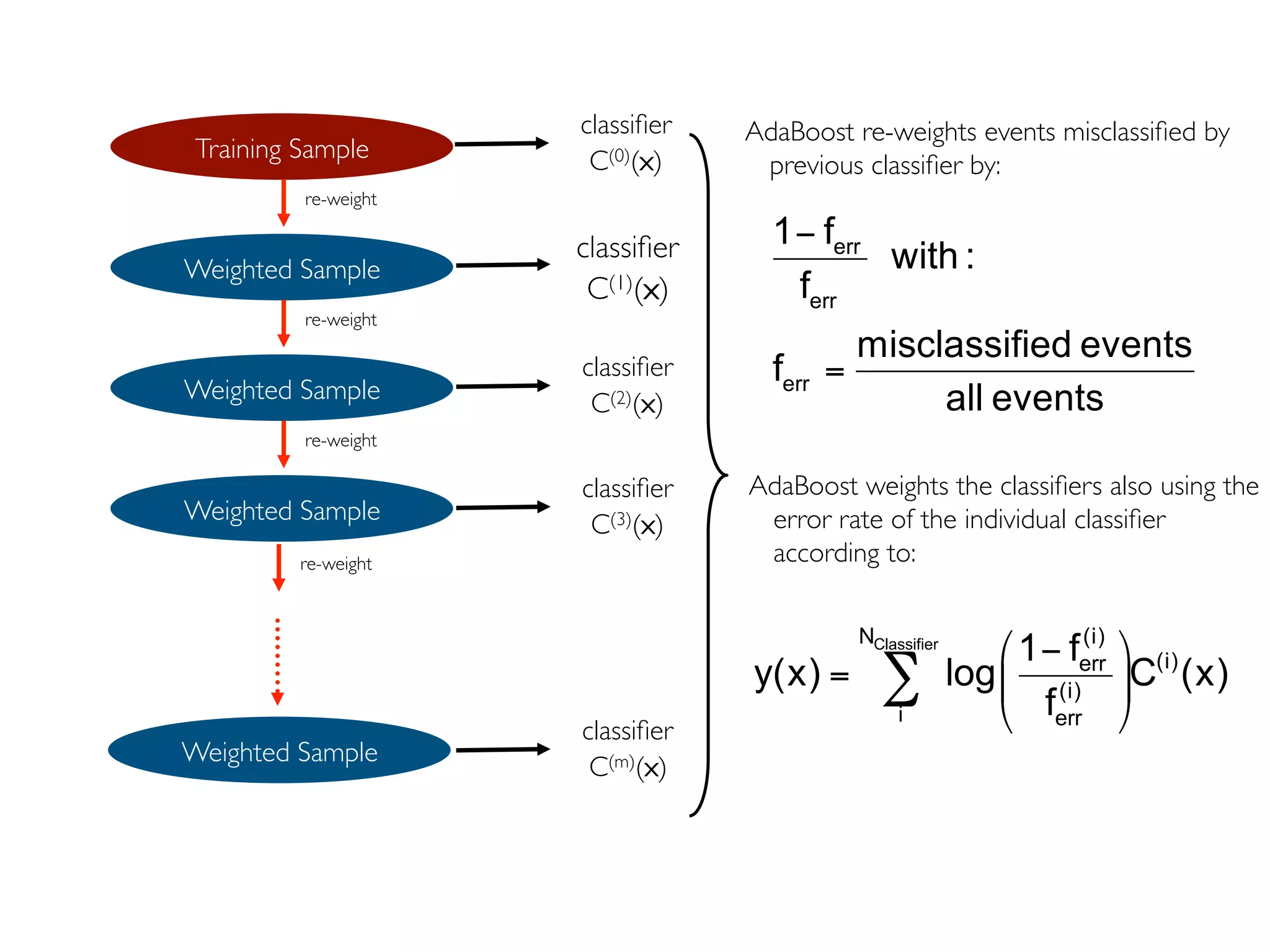
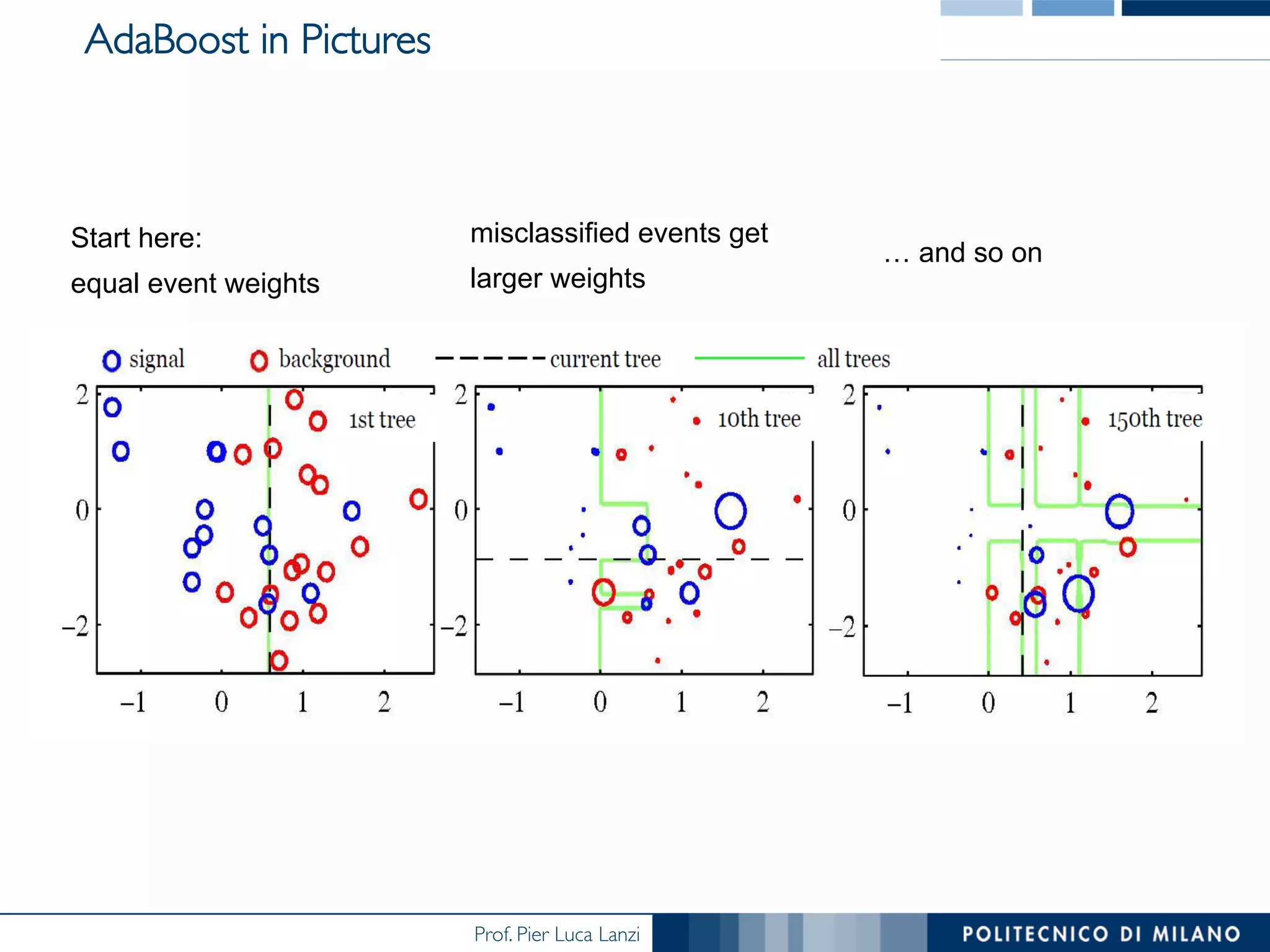
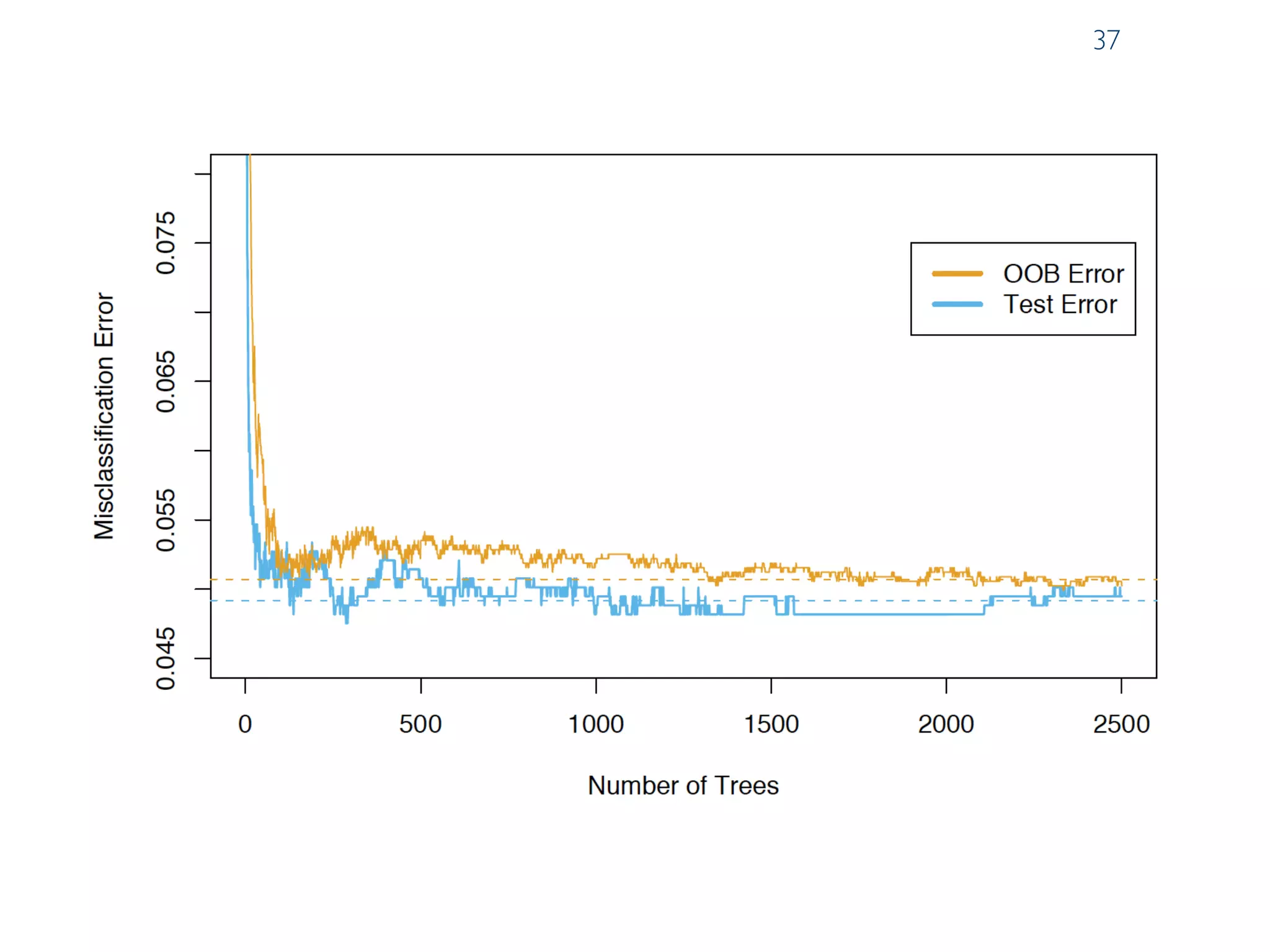
The document discusses ensemble methods in data mining, particularly focusing on techniques like bagging and boosting, which improve predictive performance by aggregating multiple classifiers. Bagging reduces variance by combining the predictions of several classifiers trained on randomized versions of the same dataset, while boosting adapts the weights of training examples based on classifier performance, thus allowing for improved focus on misclassified instances. Additionally, random forests, a specific ensemble method using decision trees, are presented as a robust and high-accuracy tool for predictions in various data scenarios.