This document presents a methodology for determining optimal locations for capacitor bank placement to enhance voltage stability in power systems. It discusses the significance of voltage stability in interconnected systems and employs static voltage stability analysis, using a reduced Jacobian method to identify ideal bus positions for reactive power injection. Results demonstrate that injecting reactive power at bus 14 yields the highest overall voltage improvement, suggesting it as a key location for capacitor installation.

1. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
INTERNATIONAL JOURNAL OF ELECTRICAL ENGINEERING &
17 – 19, July 2014, Mysore, Karnataka, India
TECHNOLOGY (IJEET)
ISSN 0976 – 6545(Print)
ISSN 0976 – 6553(Online)
Volume 5, Issue 8, August (2014), pp. 182-190
© IAEME: www.iaeme.com/IJEET.asp
Journal Impact Factor (2014): 6.8310 (Calculated by GISI)
www.jifactor.com
IJEET
© I A E M E
SELECTIVE LOCALIZATION OF CAPACITOR BANKS CONSIDERING
STABILITY ASPECTS IN POWER SYSTEMS
Nikhita S B, Suneetha M N
ME student (P&ES), electrical engineering department, university vishweshwarariah college of
engineering, Bangalore, India,
Associate professor, electrical engineering department, university vishweshwarariah college of
engineering, Bangalore, India.
182
ABSTRACT
The issue of voltage stability has become predominant in larger power systems, since the
system is operated close to its capabilities in recent years. Addressing this concern considering the
economic constraints is a challenge .This draws attention towards the localization of the reactive
components that can improve the overall voltage profile in the system. This paper discusses a
methodology for suitable selection of position (bus) for the placement of capacitor bank wherein the
injection of fixed amount of reactive power is made to depict a picture of the overall improved
voltage in the system considering the stability aspect for respective injection at that bus. The reduced
jacobian is used to determine the impact of reactive power injection in the form of system voltage
improvement.
Keywords: voltage stability index, continuous power flow, localization of capacitor bank, jacobian.
INTRODUCTION
The increase in demand for power and the increased dependency on continuous power supply
has led to tremendous increase in complexity of the system that is forced to operate close to their
limit of stability. Interconnected systems under heavily loaded conditions are much prone to collapse
caused by minor or major disturbances which might lead to blackout. Several recent blackouts are
being related to the voltage instability problems. Voltage instability is progressively uncontrollable
variations in the voltage levels. Regular overloading and the lack of reactive power are the common
grounds for voltage instability .The preventive measure to be taken in advance include reactive
power compensation, which can be done with the help of components like the capacitors. These
components being expensive and hence cannot be installed at every node.

2. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
17 – 19, July 2014, Mysore, Karnataka, India
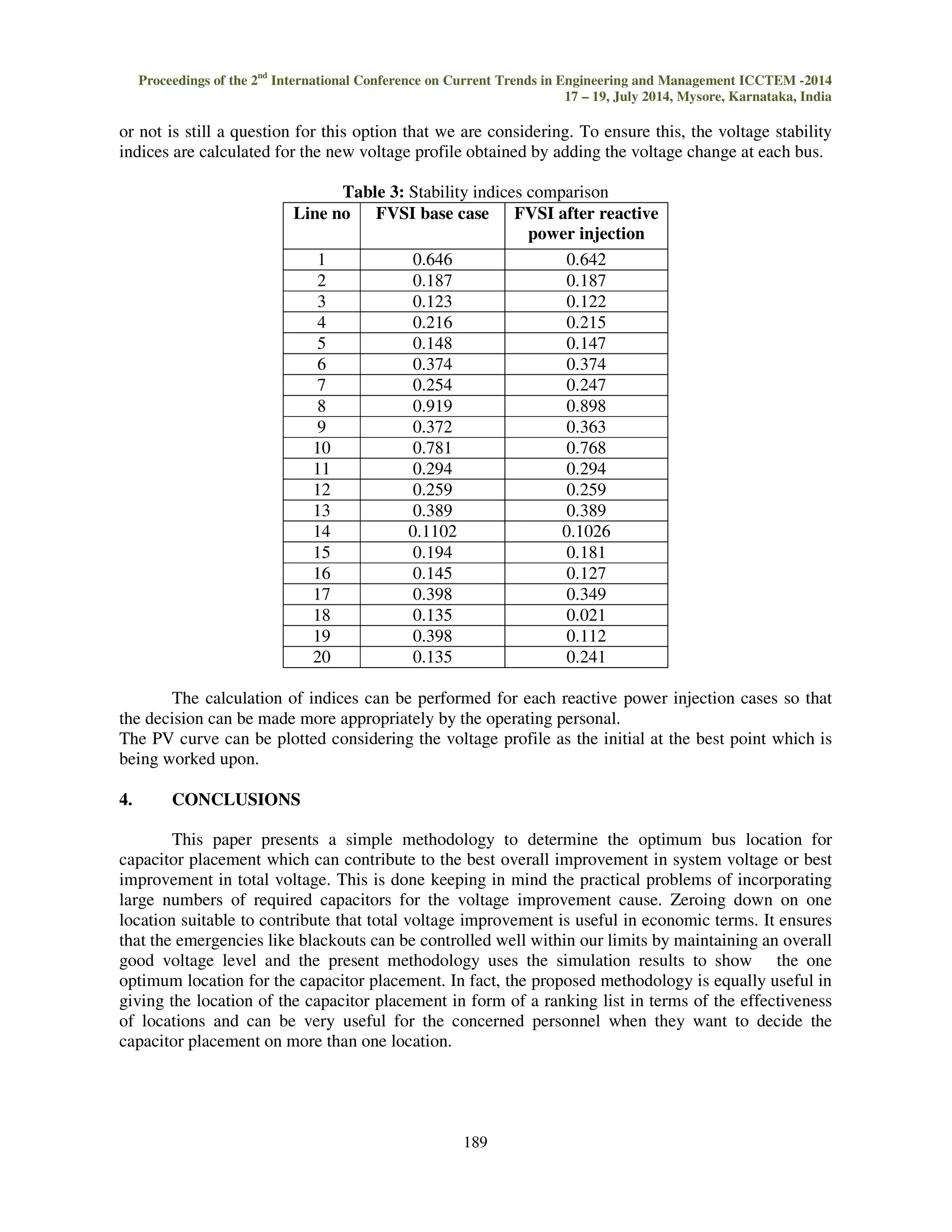
The idea of this paper is to point out the location (bus) capable of yielding the required
voltage improvement for the overall system, even if it doesn’t answer the exact amount of
compensation required. Main study in this paper involves injecting the unit amount of reactive power
into each bus which in turn enhance the voltage profile at all buses. The static voltage stability
analysis of the new voltage profile obtained at individual buses will count up to the basis of selecting
the location, which will better fit than the others.
The next section discusses the background of the technique, but they are noted in brief below:
• Conventional load flow analysis is performed using newton raphson technique
• The jacobian matrix is computed from conventional load flow. The reduced jacobian is
determined. The inverted jacobian is used to depict the change in the voltage in terms of
reactive power injection.
• This inverted jacobian is used in later section to determine the location where placing the
capacitor would yield maximum system voltage improvement.
• The voltage stability indices are used to perform the static voltage stability analysis for the new
183
voltage profile obtained
• The previous steps are repeated for a range of operating points using the continuation power
flow method and procedure is applied to each of these points.
The contribution of the proposed method lies in three major aspects firstly to determine the
capacitor location for the best overall improvement, secondly isolation of the locations which
are sure to not yield any significant improvement of the voltage and thirdly avoid the system
reaching the instability by monitoring the static stability of the system at subsequent operating
points. This procedure might turn out to be useful in situations where complete black out can be
avoided and scenario like a brownout can be improved towards the normal operating condition.
1. BACKGROUND THEORY
1.1 Computation of the reduced Jacobian
The jacobian obtained from newton raphson method is further reduced to evaluate the
suitable bus for placement of capacitors as shown in the next section. The reduced jacobian [1]
formulation is as shown below.
The matrix model of the load flow studies is given by

3. P and Q are the active and reactive power injections,
V and are the state variable vectors, namely voltage magnitude and bus angle, respectively,
P is the difference in active power injection,
Q is the difference in reactive power injection,
is the change in bus angle,
V is the change bus voltage magnitude,
J1 represents
J2 represents f / V,
J3 represents g / ,
J4 represents g / V.
The reduced Jacobian used in this technique assumes that change in active load i.e. P = 0.
Substituting this in (1), we get

4. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
17 – 19, July 2014, Mysore, Karnataka, India

5. 184
Putting from (2) and (3) we get

6. Where JR is the reduced jacobain
The reduced Jacobian would serve as the tool on which the proposed methodology, described
in detail later in this paper, would yield the results regarding the capacitor location.
1.2 Voltage stability
Voltage stability refers to ability of power systems to sustain appropriate levels of voltage
through minor and major disturbances. The voltage can be analyzed using static and dynamic
analysis approaches .Static analysis methods consider a snapshot of system operation and utilize
regular power flow equations and simulations to evaluate the maximum power transfer levels at
varying load levels. The dynamic analysis gives are useful for fast voltage collapse situation. The
dynamic analysis make use of models characterized by non linear algebraic and differential
equations solved using numerical integration methods and are time consuming and complicated
compared to that of static analysis method. Moreover it fails to provide the information on degree of
stability. The detection of critical point becomes the main aim in static voltage stability analysis. The
renowned methods of analysis are PV and QV curves, modal analysis methods, minimum singular
value methods and sensitivity analysis methods. Two popular methods used are as explained below
1.2.1 Voltage stability index
This index is an approximate measure of the closeness of the system to voltage collapse.
There are various methods of determining the voltage collapse proximity indicator. One such method
is the L-index method proposed in Kessel and Glavitsch. It is based on load flow analysis. Its value
ranges from 0 (no load condition) to 1 (voltage collapse). The bus with the highest L-index value will
be the most vulnerable bus in the system. The L-index calculation for a power sys-tem is briefly
discussed below. Consider an N-bus system in which there are Ng generators. The relationship
between voltage and current can be expressed by the following expression:
!#$ %#$#$ (5)
By segregating the load buses (PQ) from generator buses (PV), Equation (5) can write as
!
!' %
%'
%'
%''
' (
Where IG, IL and VG , VL represent currents and voltages at the generator buses and load buses.
Rearranging the above equation we get:
) *+ ,-. )/++ 0-+
1+- 2--.),+ *-. (7)
Where
3' 4%''5 4%'5

7. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
17 – 19, July 2014, Mysore, Karnataka, India
The L-index of the jth node is given by the expression:
185
?9 @ A
67 89 := ;7
A7 BC7 D D78 (8)
Where
Vi is the magnitude of the ith generator,
Vj is the voltage magnitude of the jth generator
ji is the phase angle of the term Fji
are the voltage phase angles of the generator units
Ng is the number of generating units
The values of Fji are obtained from the matrix FLG. The L-indices for a given load condition
are computed for all the load buses and the maximum of the L-indices (Lmax) gives the proximity of
the system to voltage collapse. The L-index has the advantage of indicating voltage in- stability
proximity of the current operating point without calculation of the information about the maximum
loading point.
Musirin has developed a line based stability index to indicate the stability of transmission
lines, which is termed as Fast Voltage Stability Index (FVSI). The FVSI of an l-th line can be
represented in as
3E!' F G
$H' I
Where Zl, Xl, Qr, and Vi are the line impedance, line reactance, receiving end power, and
sending end voltage respectively. It is important to note that for a stable power system, the FVSI
should be less than unity. Either of the indices is used for voltage stability analysis.
1.2.2 Continuation power flow
The main goal of the method is to observe the vagaries in voltage profile. As the technique
uses the elements of the reduced Jacobian as key, obtaining the jacobian at every operating
conditions becomes important .To avoid singularity of jacobains close to the operating limit the
method of continuous power flow is used. The method of continuation power flow is dealt with in
brief here as the different operating points are obtained in this fashion to extend the mathematics of
the previous section to all operating points. The continuation power flow, as known, is a useful tool
to plot the entire P-V curve [2-5]. i.e. to show all the operating points therein. Although the aim here
in the context of the paper is not to plot the entire operating region, the individual points can be
subjected to the mathematical analysis required and thus the change in the trend of the solution
whatever is possible to be observed over all the points. The continuation power [6-7] flow uses a
predictor-corrector scheme to solve the set of load flow equations which are reformulated to
accommodate a load parameter which denotes the increase in load from the base point. The base
point is where the continuation power flow starts from as an initial known solution.
The predictor estimates a subsequent solution point corresponding to a different load point,
the corrector corrects this solution using the conventional Newton Raphson technique, only that the
equations are slightly modified. Identifying each point is an integral part of the continuation power
flow method.

8. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM
2. PROPOSED METHODOLOGY
17 – 19, July 2014, Mysore, Karnataka, India
The reduced jacobian JR gives the relationship describing
describes V in terms of Q. The elements in each column of the inverse jacobian can be made to
represent the change in voltage of every load bus for given injection of reactive power into
corresponding to the column.
Here JR
-1 is the square matrix whose columns represent the partial derivatives of voltage of load
buses of the system wrt reactive power at load bus i,
Q represents the vector of change in reactive power modeled by a fixed amount of reactive power
injection,
V represents the vector of change in voltage.
This implies that for studying the change in voltage
injection into load buses separately or individually, the corresponding element of
must be made 1 p.u. and the others 0. Upon implementing this, the corresponding column
Directly gives V. Thus one needs to only study the elements of the particular colum
reduced Jacobian to get the change in voltage as an effect of 1 p.u. reactive power injection at that
bus i.
186
Q in terms of
. V as a result of the reactive power
eparately
. -2014
V. The inverse
the bus
Q, say Qi alone
-1.
i in JR
column i of the

9. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
17 – 19, July 2014, Mysore, Karnataka, India
-1 further gives the total improvement of system
The sum of the elements of that column i of JR
voltage Vtotali as an effect of the injection at the bus i. This is shown in (13).
On comparison of the sums of all individual columns of JR
187
-1, the bus corresponding to the column i
which yields maximum Vtotali is determined as the bus required.
Corresponding to the matrix given in (10) , bus i is not the ith bus in the system but the ith
load bus in the system as the buses involved in the analysis are only load buses. It should be noted
that the term Voverall depicts the total improvement in system voltage where as the individual
change in the bus voltage information come with the individual elements of JR
-1.Now that the voltage
change is known it is added to the actual voltage. The new voltage profile obtained is now made to
undergo static voltage stability analysis using the stability index either the l index or the fast voltage
stability index. Based on the value of the indices choice is made for the localization of the capacitor
accordingly
Further the PV curves can be drawn by conducting the continuation power flow for the range
of operating points obtained from the predictor corrector method which explains the actual distance
between the operating point and the stability limit. Here the indices are just to indicate whether the
new voltage is stable enough but since indices does not have any physical interpretation the PV
curves are used as the confirmation parameter to ensure the stability of the system. The strategy
discussed so far need not yield the same result at every operating point which is exactly why it is
quite essential to study the same aspects discussed just before at different operating points over a
continuous range. The continuation power flow aids the purpose of extending the idea discussed
before over that continuous range of operating points. The bus numbers deemed best by the
technique for capacitor placement at the operating points plotted by the continuation power flow can
be enlisted to serve as a picture to let know the same bus location is fit enough over a particular
range of operation within which any voltage recovery is possible. The range is not necessarily
required to be very near to the critical point as system recovery needing not wait till then.
Some of the advantages of this method are:
• The method is simple mathematically as it deals with
Only the elements of the inverse of the reduced Jacobian directly.
• The method gives the overall voltage improvement in
System and it ensures that the optimum bus can be found so that a condition of blackout can be
avoided and in such circumstances, some amount of voltage can be sustained in the system
with the selected capacitor(s) connected.
3. SIMULATION AND RESULTS
The IEEE 14 bus system is taking as the test system for showcasing the results obtained. The
single line diagram of 14 bus system is as shown below.

10. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
17 – 19, July 2014, Mysore, Karnataka, India
Fig 2. 14 bus system
The newton raphson method is used to perform the load flow and initial voltage and angles
are considered as base then the reduced jacobain is calculated and the inverse of it is considered
The change in voltage at each load buses when unit reactive power is injected at each bus is
calculated. Here out of nine load buses only three buses are considered to demonstrate.
Table1: Change in voltage for injection of reactive power at various buses
Bus no. Injection at bus 4 Injection at bus 10 Injection at bus 14
4 0.0413 0.0155 0.0116
5 0.0257 0.0105 0.0080
7 0.0196 0.0501 0.0375
9 0.0187 0.0962 0.0719
10 0.0155 0.1495 0.0596
11 0.0081 0.0787 0.0314
12 0.0015 0.0077 0.0278
13 0.0028 0.0145 0.0505
14 0.0117 0.0606 0.2136
Table 2: Total change in voltage in the system due to injection
Injection at bus 4 Injection at bus 10 Injection at bus 14
Overall system
voltage change
0.1449
0.4833
1.159
As seen in table the overall voltage improvement is maximum when the reactive power
injection is made at bus 14 than in other two buses considered and hence initially this can be
considered as the better bus position to localize the capacitor bank. But whether the system is stable
188

11. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
17 – 19, July 2014, Mysore, Karnataka, India
or not is still a question for this option that we are considering. To ensure this, the voltage stability
indices are calculated for the new voltage profile obtained by adding the voltage change at each bus.
Table 3: Stability indices comparison
Line no FVSI base case FVSI after reactive
189
power injection
1 0.646 0.642
2 0.187 0.187
3 0.123 0.122
4 0.216 0.215
5 0.148 0.147
6 0.374 0.374
7 0.254 0.247
8 0.919 0.898
9 0.372 0.363
10 0.781 0.768
11 0.294 0.294
12 0.259 0.259
13 0.389 0.389
14 0.1102 0.1026
15 0.194 0.181
16 0.145 0.127
17 0.398 0.349
18 0.135 0.021
19 0.398 0.112
20 0.135 0.241
The calculation of indices can be performed for each reactive power injection cases so that
the decision can be made more appropriately by the operating personal.
The PV curve can be plotted considering the voltage profile as the initial at the best point which is
being worked upon.
4. CONCLUSIONS
This paper presents a simple methodology to determine the optimum bus location for
capacitor placement which can contribute to the best overall improvement in system voltage or best
improvement in total voltage. This is done keeping in mind the practical problems of incorporating
large numbers of required capacitors for the voltage improvement cause. Zeroing down on one
location suitable to contribute that total voltage improvement is useful in economic terms. It ensures
that the emergencies like blackouts can be controlled well within our limits by maintaining an overall
good voltage level and the present methodology uses the simulation results to show the one
optimum location for the capacitor placement. In fact, the proposed methodology is equally useful in
giving the location of the capacitor placement in form of a ranking list in terms of the effectiveness
of locations and can be very useful for the concerned personnel when they want to decide the
capacitor placement on more than one location.

12. Proceedings of the 2nd International Conference on Current Trends in Engineering and Management ICCTEM -2014
17 – 19, July 2014, Mysore, Karnataka, India
190
6. REFERENCES
1. S. C. Srivastava, R. K. Varma and A. K. Tyagi, “Singularity of reduced Jacobian matrices
for identifying voltage and angle instability”, Fourth International Conference on Advances
in Power System Control,Operation and Management, 1997, APSCOM-97, vol. 2, 11-14
Nov. 1997,pp. 493 – 498.
2. T. Van Cutsem, “Voltage Instability: Phenomena, Countermeasures, and Analysis
Methods”, Proceedings of the IEEE, vol. 88, Feb. 2000, pp. 208 – 227.
3. Carson W. Taylor, “Power System Voltage Stability”, McGraw-Hill, 1994.
4. Prabha Kundur, “Power System Stability and Control”, McGraw- Hill, 1994.
5. Haque M.H, “Determination of steady state state voltage limit using PQ curve”, Power
Engineering Review, IEEE, vol.22, no. 4, pp. 71-72, April 2002.
6. Venkataramana Ajjarapu, Lowa State University, “Computational techniques for voltage
stability assessment and control”, Springer, 2006.
7. V. Ajjarapu and C. Christy, “The continuation power flow: a tool for steady state voltage
stability analysis”, IEEE Transactions on Power Systems, vol. 7, Feb. 1992, pp. 41