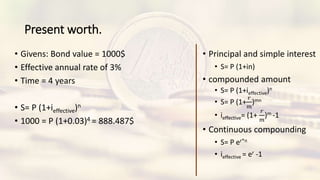1) The document discusses rules for calculating simple interest, compound interest, effective interest rates, and continuous compounding. It provides examples of calculating total amounts, interest rates, and present worth for various scenarios involving loans, bonds, and investments with different interest rates and time periods. 2) Questions are worked through calculating total amounts, interest rates, and present worth for investments with monthly, daily, semiannual compounding and continuous compounding over periods of 2, 4, 10, and 12 years. 3) Formulas used include simple interest, compound interest, effective interest rates, continuous compounding, and present worth. Results are calculated and explained for each question.

1. Economics of Chemical Plants
Section 2
Eng. Kareem H. Mokhtar

2. Rules
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1
• Where:
• S: entire amount
• P: principal
• i: nominal interest rate
• n: period in years
• r: nominal interest rate in case
there are m interest periods
per year.

3. Question 1
• It is desired to borrow 1000 $ to meet a financial obligation. This
money can be borrowed from a loan agency at a monthly interest rate
of 2 percent. Determine the following:
a) The total amount of principal plus simple interest due after 2 years if no
intermediate payments are made.
b) The total amount of principal plus compounded interest due after 2 years if
no intermediate payments are made
c) The nominal interest rate when the interest is compounded monthly
d) The effective interest rate when the interest is compounded monthly

4. The total amount of principal plus simple interest due
after 2 years if no intermediate payments are made.
• Givens: monthly interest rate = 2%, p=1000$
• Simple interest , 2 years = 24 months
• S= P (1+in)
• = 1000 (1+ [0.02*12]*2)=1480$
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

5. The total amount of principal plus compounded interest
due after 2 years if no intermediate payments are made
• Givens: monthly interest rate = 2%, p=1000$
• Compound interest , 2 years = 24 months
• S= P (1+ieffective)n
• = 1000(1+0.02)24 = 1608$
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

6. The nominal interest rate when the interest is
compounded monthly
• Givens: monthly interest rate = 2%, p=1000$
• Nominal interest , 2 years = 24 months
• Nominal interest = (interest per month* 12)
= 0.02* 12 = 0.24 = 24%
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

7. The effective interest rate when the interest is
compounded monthly
• Givens: monthly interest rate = 2%, p=1000$
• Effective interest , 2 years = 24 months
• ieffective= (1+
𝑟
𝑚
)m -1
• = (1+
0.24
12
)12 -1 = 26.82%
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

8. Question 2
• For the case of a nominal annual interest rate of 20 percent,
determine
a) The total amount to which one dollar of initial principal would accumulate
after one 365 day year with daily compounding.
b) The total amount to which one dollar of initial principal would accumulate
after one year with continuous compounding.
c) The effective annual interest rate if compounding is continuous

9. The total amount to which one dollar of initial principal
would accumulate after one 365 day year with daily
compounding.
• Givens: nominal annual interest= 20%
• daily compounding.
• S= P (1+
𝑟
𝑚
)mn
• = (1+
0.2
365
)365 = 1.2213$
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

10. The total amount to which one dollar of initial principal
would accumulate after one year with continuous
compounding.
• Givens: nominal annual interest= 20%
• continuous compounding.
• S= P er*n
• = 1 e0.2*1 = 1.2214$
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

11. The effective annual interest rate if compounding is
continuous
• Givens: nominal annual interest= 20%
• effective annual interest, compounding is
continuous
• ieffective = er -1 = e0.2 -1 =22.14%
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

12. Question 3
• bond has a maturity value of $1000 and is paying discrete compound
interest at an effective annual rate of 3 percent. Determine the
following at a time four years before the bond reaches maturity value:
a) Present worth.
b) Discount.
c) Discrete compound rate of effective interest which will be received by a
purchaser if the bond were obtained for $700.
d) Repeat part (a) for the case where the nominal bond interest is 3 percent
compounded continuously.

13. Present worth.
• Givens: Bond value = 1000$
• Effective annual rate of 3%
• Time = 4 years
• S= P (1+ieffective)n
• 1000 = P (1+0.03)4 = 888.487$
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

14. Discrete compound rate of effective interest which will
be received by a purchaser if the bond were obtained for
$700.
• Givens: Bond value = 1000$
• Effective annual rate =?
• Time = 4 years
• S= P (1+ieffective)n
• 1000= 700 (1+ieffective)4
• Ieffective = 9.33%
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

15. Repeat part (a) for the case where the nominal bond
interest is 3 percent compounded continuously.
• Givens: Bond value = 1000$
• Nominal annual rate of 3%
• Time = 4 years
• S= P er*n
• 1000= P e0.03*4 = 886.92$
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

16. Question 4
• It is desired to have $9000 available 12
years from now. If $5000 is available for
investment at the present time, what
discrete annual rate of compound
interest on the investment would be
necessary to give the desired amount?
• S= P (1+ieffective)n
• ieffective = 5%
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

17. Question 5
• What will be the total amount
available 10 years from now if $2000
is deposited at the present time with
nominal interest at the rate of 6
percent compounded semiannually?
• S= P (1+
𝑟
𝑚
)mn
• 3612.22 $
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1

18. Question 6
• An original loan of $2000 was made at 6
percent simple interest per year for 4
years. At the end of this time, no interest
had been paid and the loan was
extended for 6 more years at a new,
effective, compound-interest rate of 8
percent per year. What is the total
amount owed at the end of the 10 years
if no intermediate payments are made?
• S= 3935$
• Principal and simple interest
• S= P (1+in)
• compounded amount
• S= P (1+ieffective)n
• S= P (1+
𝑟
𝑚
)mn
• ieffective= (1+
𝑟
𝑚
)m -1
• Continuous compounding
• S= P er*n
• ieffective = er -1