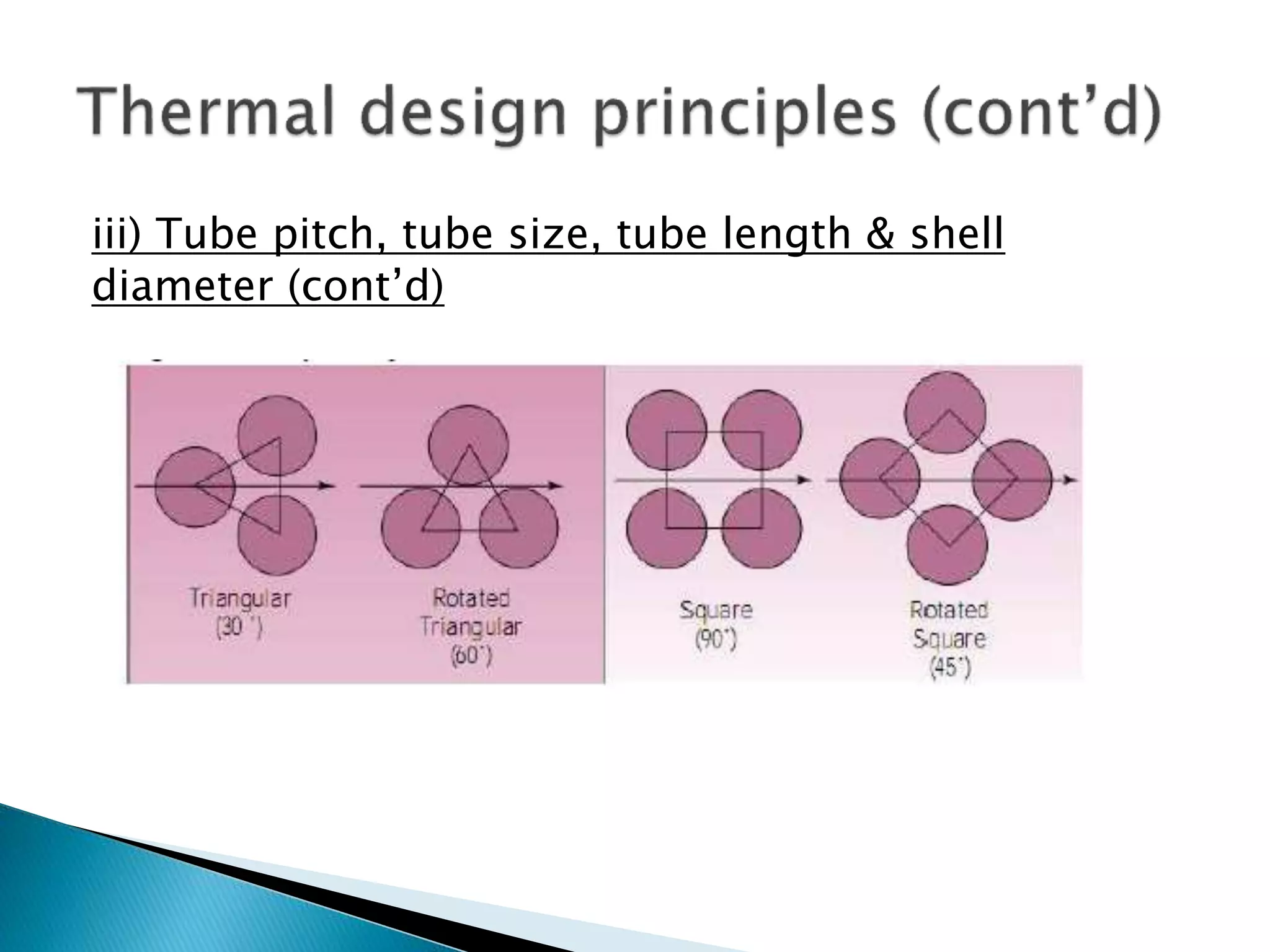
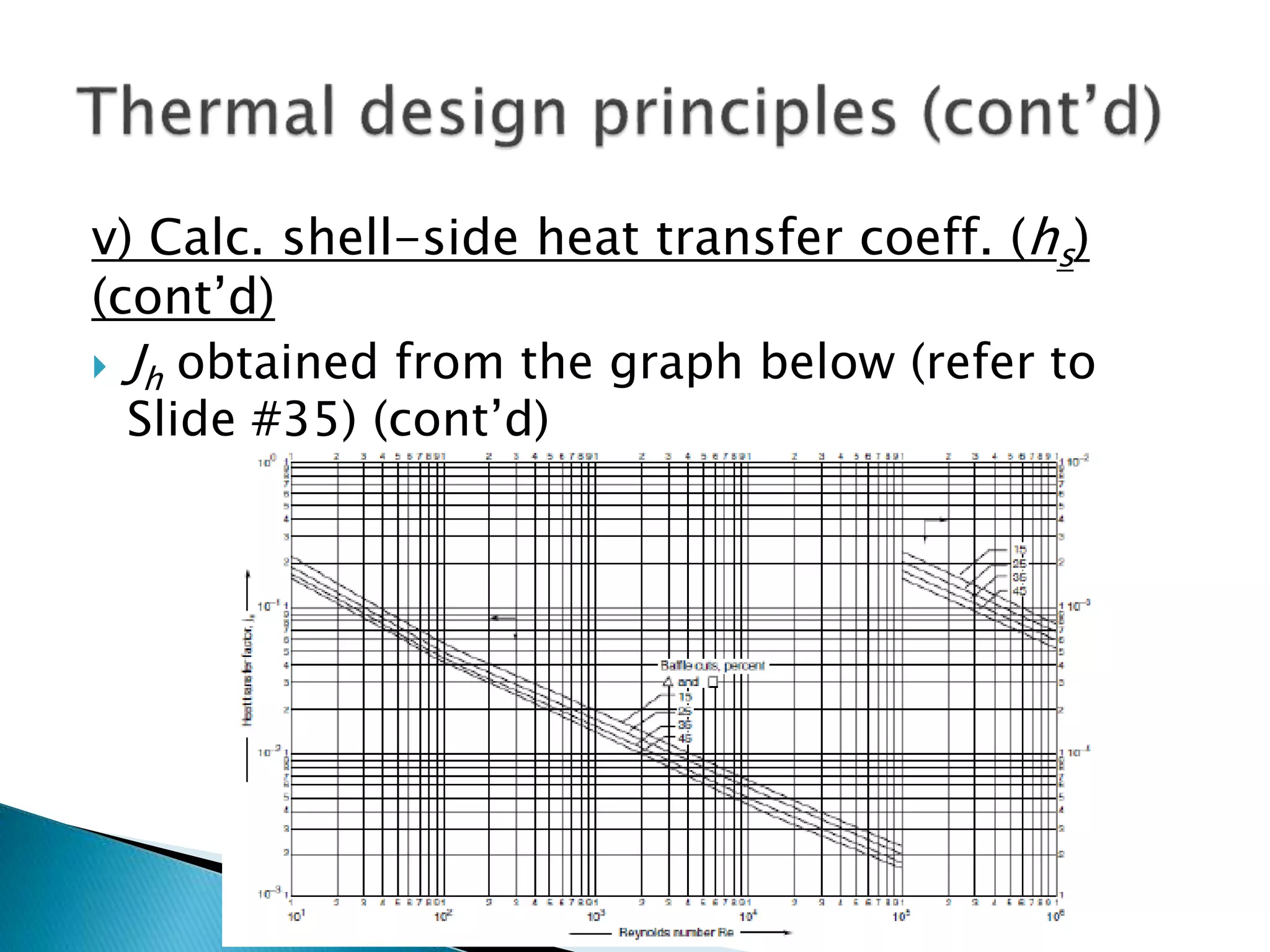
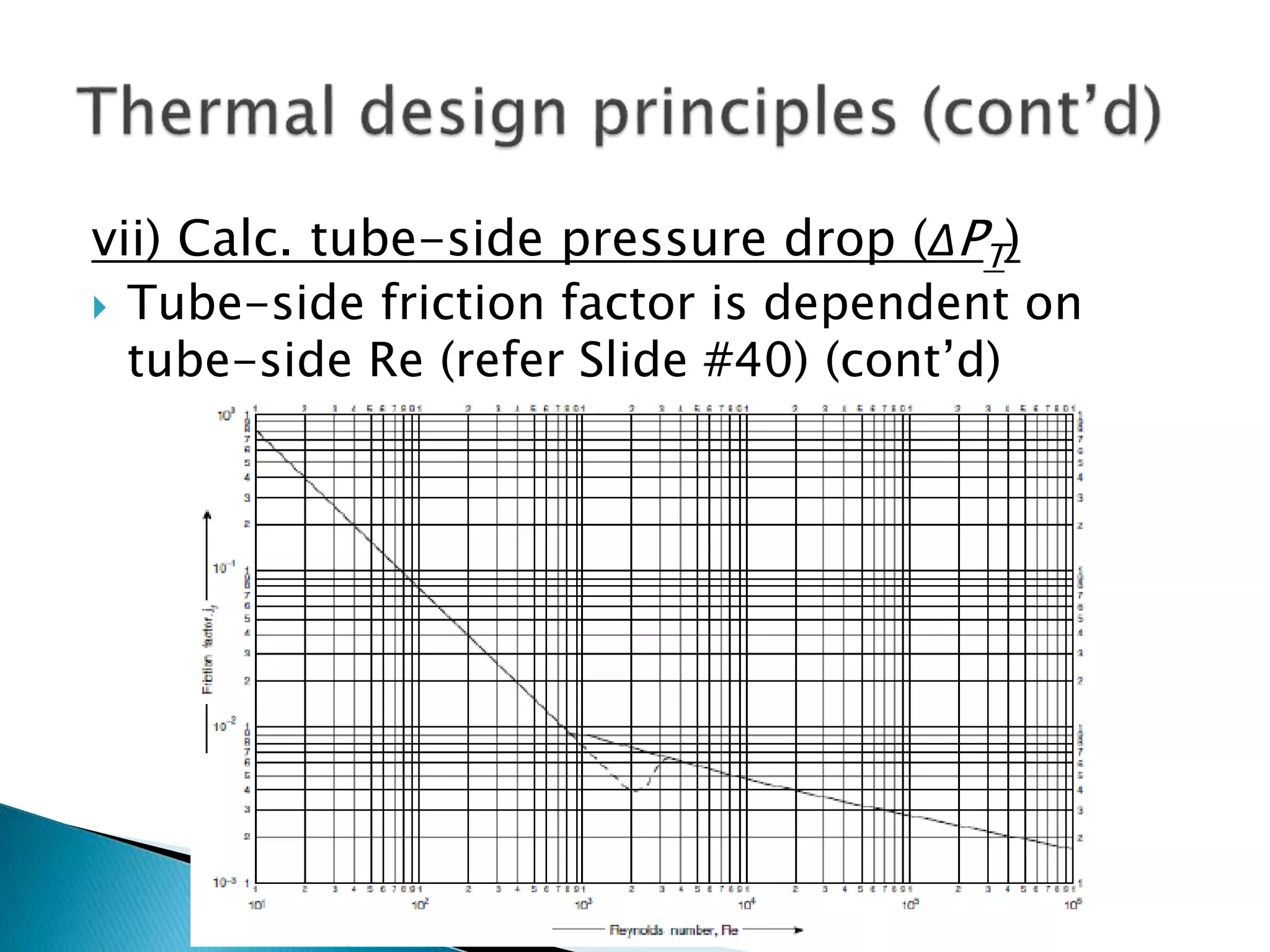
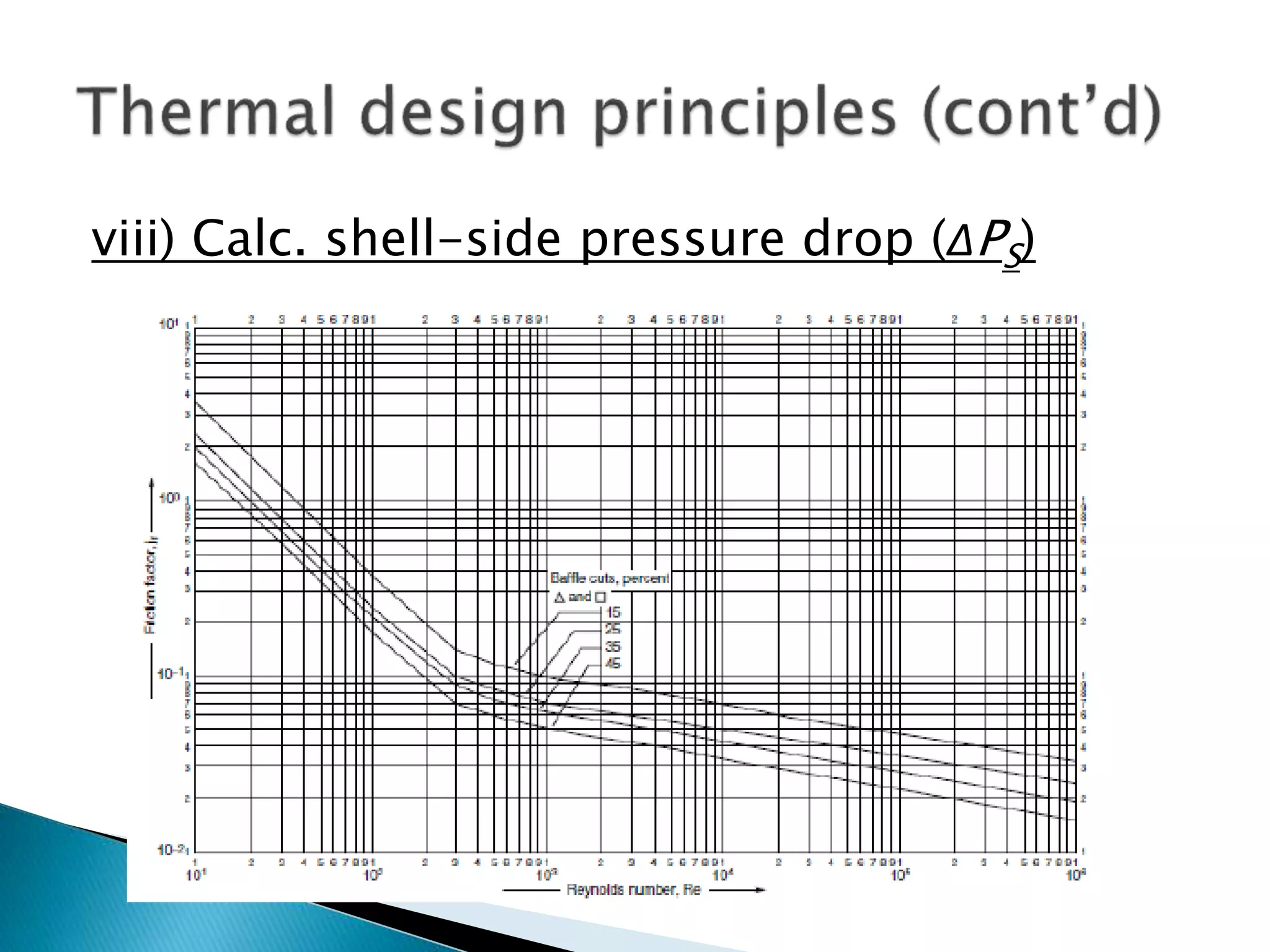
The document discusses the design and operational principles of shell and tube heat exchangers, including fluid flow arrangements (counter-current vs. co-current) and thermal design calculations. Key topics covered include determining overall duty, heat transfer coefficients, tube design specifications, and pressure drop calculations for both tube-side and shell-side fluids. The document emphasizes the importance of various design factors such as fluid type, viscosity, and layout for optimizing heat transfer efficiency.

1. Author: Vikram Sharma
Date: 20th February 2017

2.  What is a S&T HEX?
 Fluid flow in HEX – counter vs. co-current
 Fluid allocation in S&T Heat Exchanger
 Thermal design principles
◦ Overall duty determination
◦ Initial heat transfer area (Ao)
◦ Tube pitch, tube size, tube length & shell diam.
◦ Calc. tube-side heat transfer coeff. (hi)
◦ Calc. shell-side heat transfer coeff. (hs)
◦ Calc. overall heat transfer coeff. (Uo)
◦ Calc. tube-side pressure drop (ΔPT)
◦ Calc. shell-side pressure drop (ΔPS)
 Summary

3.  As per Wikipedia, it consist of a shell (a large
pressure vessel) with a bundle of tubes inside
it.
 One fluid flows through the tube and the
second fluid flows through the shell.
 Heat transfer occurs when the fluid in the
shell flows over the tubes.

4.  Counter-current flow:
◦ Fluids are flowing in the opposite direction
 Co-current flow:
◦ Fluids are flowing in the parallel direction
 Why counter-current is preferred over co-
current?
◦ Thermal stresses are minimized due to more
uniform ΔT between two fluids;
◦ Cold fluid temp. can approach the inlet temp. of the
hot fluid; and
◦ More uniform of HEX can be achieved – uniform ΔT
throughout the HEX

5.  Fouling fluids:
◦ Should be placed in tube-side;
 Corrosive fluids:
◦ Should be placed in tube-side as to minimize the
purchase of expensive alloys & cladding material;
 High temperature fluid:
◦ Use of expensive alloys
 High pressure fluid
◦ Minimize the cost of construction of mechanically strong
shell.
 High viscosity fluids:
◦ Shell-side provided it is at turbulent flow (Re>200).
Viscous fluids in tube-side results to high ΔP

6. i) Overall duty determination
 Begins with the determination of duty of the
heat exchanger.

7.  In calculating t2, the Cp of the other fluid taken at
t1.
 Once t2 is calculated, a mean temp. of t1 & t2 is
computed.
 This mean temp. is used as ref. to obtain the Cp of
the other fluid.
 An iterative procedure is carried out to determine if
the Cp of the other fluid is insignificant, the Cp is
taken as the mean temp.

8. ii) Initial heat transfer area (Ao)
 Calculate the Log Mean Temp. Different (LMTD).
 Assumption underlying LMTD are:
◦ No change in specific heats;
◦ Constant Uo
◦ No heat losses
 The corrected log mean temp. difference (ΔTm) is a
f(FT, LMTD).

9. ii) Initial heat transfer area (Ao) (cont’d)
 Correction factor (FT) shall not be < 0.75 due to:
◦ Inefficient use of heat transfer area;
◦ Violating the simplifying assumptions used in this approach
◦ Uncertainties in design data have more significant effect
when the slopes are steep
 The initial heat transfer area is calculated by:

10. ii) Initial heat transfer area (Ao) (cont’d)
 Uo is selected based on the service of the HEX

11. ii) Initial heat transfer area (Ao) (cont’d)
 Calculate the corrected log mean temp. difference
(ΔTm).
 1st, LMTD is calculated using inlet and out temp. of HEX
 The above is for counter-current HEX
 For co-current, the terminal temp. difference shall be
(T1-t1) and (T2-t2)

12. ii) Initial heat transfer area (Ao) (cont’d)
 The LMTD equation is based on the following
assumptions:
◦ No change in specific heats;
◦ Constant heat transfer coefficients; and
◦ No heat losses
 Once the ΔTm, Uo and Q are determined, calculate the Ao
(refer to Slide #9)

13. iii) Tube pitch, tube size, tube length & shell
diameter
 Four (4) tube pitch layout:
◦ Triangular (30°)
◦ Rotated Triangular (60°)
◦ Square (90°)
◦ Rotated Square (45°)
 Adv. & Disadv. of triangular pitch layout?
◦ Accommodate more tubes than other patterns
◦ Produce high turbulence → better heat transfer
◦ Typical pt = 1.25do → restricts mech. cleaning of tubes to
restricted access lanes
◦ Preferred when the diff. in OP between 2 fluids are significant

14. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Adv. & Disadv. of Triangular pitch layout? (cont’d)
◦ Limited to clean shell-side services
◦ Can be used in dirty shell-side services if a suitable &
effective chem. cleaning is available.
 Adv. & Disadv. Of Square pitch layout?
◦ Typicallly used for dirty shell-side services & when mech.
Cleaning is required
◦ Not used in the fixed head design as cleaning is unfeasible
◦ Used when the shell-side Re < 2,000 to induce higher
turbulence

15. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 pt = 1.25do → smallest shell dia. for a given number of
tubes
 Min. tube pitch for triangular pattern shall be:
◦ pt = 1.25do
 TEMA also recommends an additional min. 6mm of
cleaning lane between adjacent tubes for square pitch
 Min. tube pitch for square pitch shall be:
◦ Max (pt = 1.25do ; do + 6mm)

16. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)

17. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Tube sizes ranging from ¼” (6.350mm) to 2” (50mm)
 Smaller tube size → more compact & economical size
HEX
 Larger tube size → heavy fouling & ease via mech.
Cleaning
 Preferred length of HEX tubes → 6ft (1.83m), 8ft
(2.44m), 12ft (3.66m), 16ft (4.88m), 20ft (6.10m) & 24ft
(7.32m)

18. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Once the tube size is selected, calculate the area of 1
tube (A1,tube)
 Calc. the tube-side velocity. Ensure the fluid velocity
conforms to the requirement (refer next Slide #18)

19. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Calc. the tube-side velocity. Ensure the fluid velocity
conforms to the requirement (cont’d)

20. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 If Ut is within the limits but at the lower side, select
smaller tube size & repeat the calc. above.
 Adequacy is determined frm. the tube-side pressure
drop!
 Next, calc. tube bundle dia. (Db) (mm)
 BS 3274: HEX dia. Frm 6” (150mm) → 42” (1,067mm)
 TEMA: shell dia. → 60” (1,520mm)

21. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 TEMA: shell dia. → 60” (1,520mm) (cont’d):
 Parameter K1 & n1 tube pitch & no. of tube passes

22. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 K1 & n1 → tube pitch type & no. of tube passes (cont’d)

23. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Shell inner dia. (Ds) → find out the shell-bundle
clearance
 Shell bundle clearance → type of HEX rear head
◦ Pull through floating heads (Type T)

24. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Shell bundle clearance → type of HEX rear head (cont’d)
◦ Split-Ring floating heads (Type S)
◦ Outside packed floating heads (Type P)

25. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Shell bundle clearance → type of HEX rear head (cont’d)
◦ Fixed tube sheet (Type L, M & N)
◦ U-tube (Type U)

26. iii) Tube pitch, tube size, tube length & shell
diameter (cont’d)
 Shell bundle clearance → type of HEX rear head (cont’d)
◦ Externally sealed tube sheets (Type W)
 Ds = Db + Shell-bundle clearance
◦ Convert Db & Shell-bundle clearance frm. mm → m

27. iv) Calc. tube-side heat transfer coeff. (hi)
 First, calc. the tube-side Reynolds number
 Re < 2,100 Laminar
 Re > 10,000 Turbulent

28. iv) Calc. tube-side heat transfer coeff. (hi)
 If 100 < Re < 2,100, use Sieder-Tate’s eq.
◦ Nu ≥ 3.5, if Nu < 3.5 → Nu = 3.5

29. iv) Calc. tube-side heat transfer coeff. (hi)
 If Re > 10,000, use Sieder-Tate’s eq.
◦ With 0.7 < Pr < 700 & L/Ds > 60
 If 40,000 < Re < 100,000, use ESDU eq.
◦ With 0.7 < Pr < 160 & L/Ds > 60

30. iv) Calc. tube-side heat transfer coeff. (hi)
 Transitional regime shall be avoided for
design, if cannot:
◦ Min. (Nu from Slide #28, Nu from Slide #29)
◦ Nu from Slide #28 & #29 are Sieder-Tate’s eq.
v) Calc. shell-side heat transfer coeff. (hs)
 Calc. baffle spacing (B). Why have baffles?
◦ Tube support
◦ Maintain suitable shell-side fluid velocity
◦ Prevent tube failure due to flow induced vibration

31. v) Calc. shell-side heat transfer coeff. (hs)
(cont’d)
 Baffle spacing (B): Max. (Ds/5; 2 in.) → ensure
same units
 Max baffle spacing (B) is:
 Max baffle spacing is expressed in inches
 Baffle cut of 25% is used, can vary from 15%
→ 45%
 Why? → Kern’s shell-side ΔP is based on 25%

32. v) Calc. shell-side heat transfer coeff. (hs)
(cont’d)
 Calc. shell-side cross flow area (As):
 Calc. linear velocity (Us) (0.3m/s<Us<1.0m/s)

33. v) Calc. shell-side heat transfer coeff. (hs)
(cont’d)
 Calc. shell-side equiv. dia. (de) → based on
type of tube pitch
 Calc. shell-side Re → to obtain the Shell-side
heat transfer factor (jh) (Refer Slide #34)

34. v) Calc. shell-side heat transfer coeff. (hs)
(cont’d)
 Calc. hs: (units same as tube-side)
 Jh obtained from the graph below (refer to
Slide #35)

35. v) Calc. shell-side heat transfer coeff. (hs)
(cont’d)
 Jh obtained from the graph below (refer to
Slide #35) (cont’d)

36. vi) Calc. overall heat transfer coeff. (Uo)
 Uo → reciprocal of the overall resistance to
heat transfer & it’s a sum of several heat
transfer resistances
 Each resistance depend on several factors:
◦ Physical properties of fluids
◦ Heat transfer process (conduction, convection,
condensation, boiling or radiation)
◦ Physical arrangement of the heat transfer surface

37. vi) Calc. overall heat transfer coeff. (Uo)
 Each resistance depend on several factors:
◦ Physical arrangement of the heat transfer surface
(cont’d)

38. vi) Calc. overall heat transfer coeff. (Uo)
 The Uo calc. shall not be taken as the final
answer
 Compare it with the assumed Uo frm. Slide
#10
 Uo from Slide #37 should be 30% of Uo,ass
from Slide #10
 If not, repeat calc. starting from Slide #9

39. vii) Calc. tube-side pressure drop (ΔPT)
 ΔPT calc. from:
 Index m is a f(fluid flow regime)
◦ Laminar flow (Re < 2,100), m = 0.25
◦ Turbulent flow (Re > 2,100) m = 0.14
 Tube-side friction factor is dependent on
tube-side Re (refer Slide #40)

40. vii) Calc. tube-side pressure drop (ΔPT)
 Tube-side friction factor is dependent on
tube-side Re (refer Slide #40) (cont’d)

41. vii) Calc. tube-side pressure drop (ΔPT)
 ΔPT shall be within the specifications
 If lower than specs, select diff. tube dimensions &
layout, repeat the calcs. frm. Slide #18.
viii) Calc. shell-side pressure drop (ΔPS)
 ΔPS shall be within the specifications
 Similar approach as (vi), obtain jf from Slide #42.

42. viii) Calc. shell-side pressure drop (ΔPS)