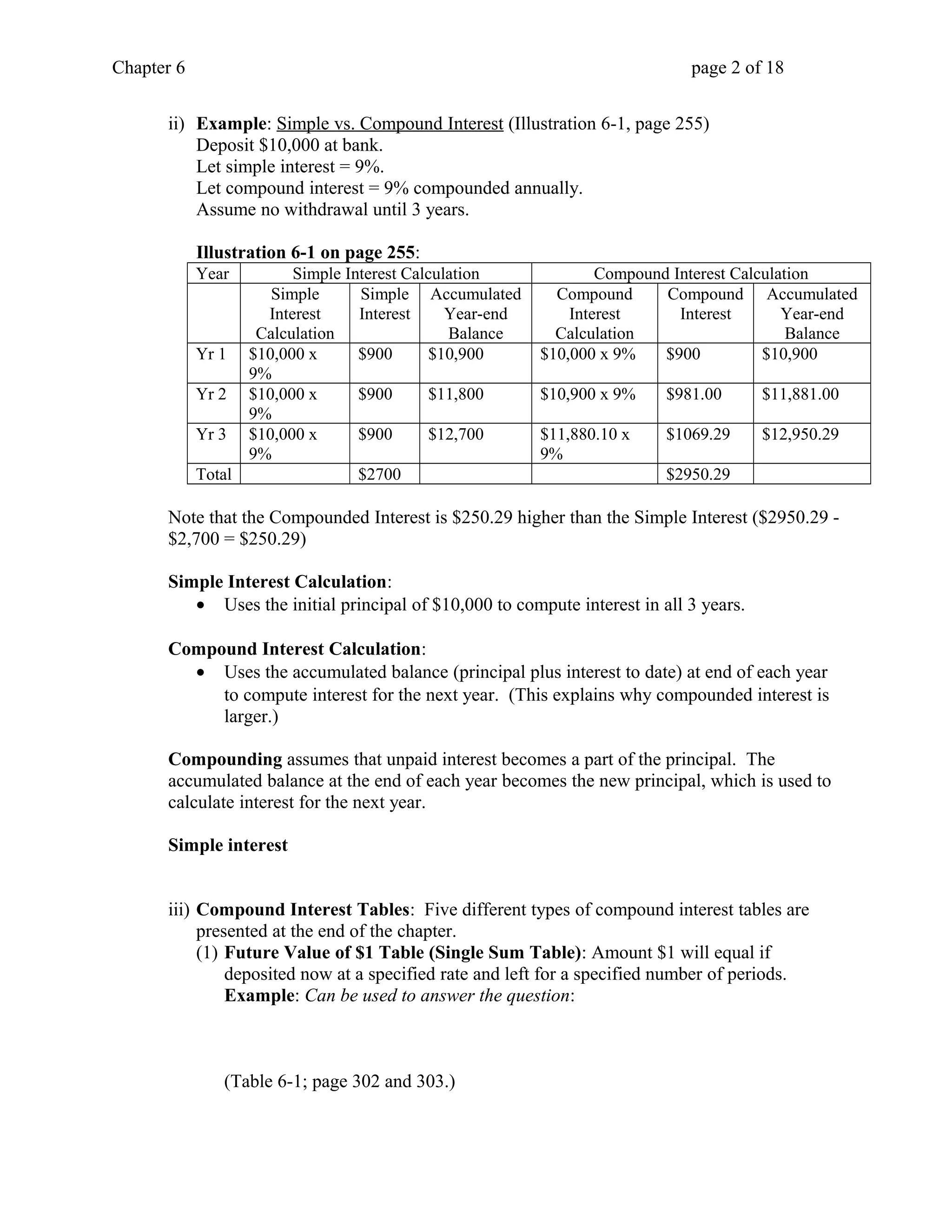
This document provides an overview of key concepts related to accounting and the time value of money. It discusses the basic premise that a dollar today is worth more than a dollar in the future due to interest-earning potential. It also covers compound interest calculation methods and the use of interest tables to solve for unknown variables. Specific topics covered include single-sum problems involving future and present value, annuities, and the calculation of future and present value for both ordinary annuities and annuities due. Worked examples are provided throughout to illustrate the application of time value of money formulas and tables.

1. Chapter 6 page 1 of 18
Chapter 6: Accounting and the Time Value of Money
1) Basic Time Value Concepts:
Time Value (TV) of Money: A dollar received today is worth more than a dollar promised at
some time in the future. This relationship exists because of the opportunity to invest today’s
dollar and receive interest on the investment.
a Applications of Time Value Concepts:
i) Used for making decisions about Notes, Leases, Pensions and Other Postretirement
Benefits, Long-Term Assets, Sinking Funds, Business Combinations, Disclosures,
and Installment Contracts.
ii) Also, TV concepts are very important in personal finance and investment decisions.
For example, TV of Money is used when purchasing home or car, planning for
retirement, and deciding on investments.
b The Nature of Interest:
i) Interest :
ii) Amount of Interest in transaction is function of three variables:
(1) Principal :
(2) Interest Rate :
(3) Time :
The larger the principal the larger the dollar amount of interest.
The higher the interest rate the larger the dollar amount of interest.
The longer the time period the larger the dollar amount of interest.
c Simple Interest:
d Compound Interest:
i)

2. Chapter 6 page 2 of 18
ii) Example: Simple vs. Compound Interest (Illustration 6-1, page 255)
Deposit $10,000 at bank.
Let simple interest = 9%.
Let compound interest = 9% compounded annually.
Assume no withdrawal until 3 years.
Illustration 6-1 on page 255:
Year Simple Interest Calculation Compound Interest Calculation
Simple
Interest
Calculation
Simple
Interest
Accumulated
Year-end
Balance
Compound
Interest
Calculation
Compound
Interest
Accumulated
Year-end
Balance
Yr 1 $10,000 x
9%
$900 $10,900 $10,000 x 9% $900 $10,900
Yr 2 $10,000 x
9%
$900 $11,800 $10,900 x 9% $981.00 $11,881.00
Yr 3 $10,000 x
9%
$900 $12,700 $11,880.10 x
9%
$1069.29 $12,950.29
Total $2700 $2950.29
Note that the Compounded Interest is $250.29 higher than the Simple Interest ($2950.29 -
$2,700 = $250.29)
Simple Interest Calculation:
· Uses the initial principal of $10,000 to compute interest in all 3 years.
Compound Interest Calculation:
· Uses the accumulated balance (principal plus interest to date) at end of each year
to compute interest for the next year. (This explains why compounded interest is
larger.)
Compounding assumes that unpaid interest becomes a part of the principal. The
accumulated balance at the end of each year becomes the new principal, which is used to
calculate interest for the next year.
Simple interest
iii) Compound Interest Tables: Five different types of compound interest tables are
presented at the end of the chapter.
(1) Future Value of $1 Table (Single Sum Table): Amount $1 will equal if
deposited now at a specified rate and left for a specified number of periods.
Example: Can be used to answer the question:
(Table 6-1; page 302 and 303.)

3. Chapter 6 page 3 of 18
(2) Present Value of $1 Table: Amount that must be deposited now at a specified
rate of interest to equal $1 at the end of a specified number of periods. Example:
Can be used to answer the question:
(Table 6-2; page 304 and 305.)
(3) Future Value of an Ordinary Annuity of $1 Table: Amount to which payments
of $1 will accumulate if payments are invested at END of each period at specified
rate of interest for specified number of periods. Example: Can be used to
answer the question:
(Table 6-3; page 306 and 307.)
(4) Present Value of an Ordinary Annuity of $1 Table: Amount that must be
deposited now at a specified rate of interest to permit withdrawals of $1 at the
END of regular periodic intervals for specified number of periods. Example:
Can be used to answer the question:
(Table 6-4; page 308 and 309.)
(5) Present Value of an Annuity due of $1 Table: Amounts that must be deposited
now at a specified rate of interest to permit withdrawals of $1 at the BEGINNING
of regular periodic intervals for the specified number of periods. Example: Can
be used to answer the question:
(Table 6-5; page 310 and 311.)

4. Chapter 6 page 4 of 18
(6) General:
(a) Compound tables are computed using basic formulas.
(b)
(i) TO CONVERT ANNUAL INTEREST RATE TO COMPOUNDING
PERIODIC INTEREST RATE:
(ii) TO DETERMINE THE NUMBER OF PERIODS:
(c) Frequency of Compounding: (Illustration 6-4 page 257)
This illustration shows how to determine:
(1) Interest rate per compounding period.
(2) Number of compounding periods in four different scenarios.
12% Annual
Interest Rate over
5 years
Compounded
Interest Rate per
Compounding
Period
Number of Compounding Periods
Annually (1) 0.12/1 = 0.12 5 yrs x 1 period per yr = 5 periods
Semiannually (2) 0.12/2 = 0.06 5 yrs x 2 period per yr = 10 periods
Quarterly (4) 0.12/4 = 0.03 5 yrs x 4 period per yr = 20 periods
Monthly (12) 0.12/12 = 0.01 5 yrs x 12 period per yr = 60 periods
(d) Definitions:
Example: Assume 9% annual interest compounded DAILY provides a 9.42%
yield, or a difference of 0.42%.
Effective rate: The 9.42 % is referred to as the effective yield.
Stated rate (or nominal rate or face rate): The 9% is referred to as the
stated rate.
Relationship between effective and stated rate: When compounding
frequency is greater than once a year, the effective interest rate will always be
greater than the stated rate.

5. Chapter 6 page 5 of 18
e Fundamental Variables: The following four variables are fundamental to all compound
interest problems:
i) Interest Rate: Unless otherwise stated, the rate given is the annual rate that must be
adjusted to reflect length of compounding period if less than a year.
ii) Number of Time Periods: Number of compounding periods (An individual period
may be equal to or less than 1 year.)
iii) Future Value: Value at a future date given sum(s) invested assuming compound
interest.
iv) Present Value: Value now (present time) of future sum(s) discounted assuming
compound interest.
In some cases, all four variables are known. However, many times at least one
variable is unknown.
2) Single-Sum Problems:
Two categories of single-sum problems:
a Future Value of a Single Sum:
i) Compute unknown future value of known single sum of money invested now for
certain number of periods (n) at a certain interest rate (i).
ii)
iii) Determine future value of single sum: Multiply the future value factor (FVF) by its
present value (principal).
( ) n,i FV =PV FVF
where FV = future value; PV = present value; FVF= future value factor for n periods
at i interest.
iv) Example 1: (p 260)
What is future value of $50,000 invested for 5 years compounded annually at 11%?
FV = PV(FVF)
FV =
FV =
(To get the ___________FVF, look at Table 6-1 on page 303. The ___% column and
____-period row gives the future value factor of ___________.)

6. Chapter 6 page 6 of 18
v) Example 2: (p260)
What is the future value of $250 million if deposited in 2002 for 4 years if interest is
10%, compounded semi-annually?
FV=PV(FVF)
FV=
FV=
(To get the ________, look at Table 6-1 which is the Future Value of $1 table. This
is the table used to figure out the future value of $1 invested today. To get the
number of
periods,______________________________________________________. Thus,
there are ______ periods. To get the correct semi-annual interest rate,
____________________________________. This gives us a
______________________________________We use n= ___ (number of periods)
and i=____% (interest rate) to find the correct FVF.)
b Present Value of a Single Sum:
i)
ii) Compute unknown present value of known single sum of money in the future that is
discounted for n periods at i interest rate.
iii)
iv) Determine present value of single sum:
( ) n,i PV =FV PVF
where PV = present value; FV = future value; PVF = present value factor for n
periods at i interest.

7. Chapter 6 page 7 of 18
v) Example 1: (page 261-262)
What is the present value of $84,253 to be received or paid in 5 years discounted at
11% compounded annually?
PV=FV(PVF)
PV=
PV=
(To get the __________ PVF, look at Table 6-2 on page 305. The ___% column and
____-period row gives the present value factor of _________.)
vi) Example 2: (page 262)
If we want $2,000 three years from now and the compounded interest rate is 8%, how
much should we invest today?
PV=FV(PVF)
PV=
PV=
(To get the __________ PVF, look at Table 6-2, page 305. The ____% column and
the ___-period row give the PVF of __________.)
c Solving for Other Unknowns in Single-Sum Problems: Unlike the examples given
above, many times both the future value and present value are known, but the number of
periods or the interest rate is unknown. If any three of the four values (FV, PV, n, i) are
known, the remaining unknown variable can be derived.
i) Illustration – Computation of the Number of Periods:
How many years will it take for a deposit of $47,811 at 10% compounded annually to
accumulate to $70,000?
Solution 1:
( ) n,10% FV = PV FVF
FVF=
FVF=
Look at Table 6-1, Future Value of $1. Look at ____% column and find the
calculated FVF of _________. We find this factor in the row n= ____. Thus, it will
take ___________.

8. Chapter 6 page 8 of 18
Solution 2:
( ) n,10% PV = FV PVF
PVF =
PVF =
Look at Table 6-2, Present Value of $1. Look at ____% column and find the
calculated PVF of _________. We find this factor in the row n=___. Thus, it will
take ____________.
ii) Illustration – Computation of the Interest Rate:
What is the interest rate needed if we invest $800,000 now and want to have
$1,409,870 five years from now?
Solution 1:
( ) 5,i FV =PV FVF
FVF =
FVF =
Look at Table 6-1 p 303, Future Value of $1. Look at row n=____ and find the
calculated FVF of _______. We find this factor in the column i = ___%. Thus, we
would need an interest rate of ___%.
Solution 2:
( ) 5,i PV =FV PVF
PVF =
PVF =
Look at Table 6-2 p 305, Present Value of $1. Look at row n=____ and find the
calculated PVF of ________. We find this factor in the column for ____%. Thus,
we would need an interest rate of _____%.
3) Annuities:

9. Chapter 6 page 9 of 18
a General:
i) Up to this point, we have only worked with discounting a single sum. However,
many times a series of dollar amounts are to be paid (received) periodically (ex:
loans, sales on installments, invested funds recovered in intervals)
ii) Annuity :
Requires
(1)
(2)
(3)
iii) The future value of an annuity is the sum of all the rents plus the accumulated
compound interest on them.
iv) NOTE:
(1) Ordinary Annuity :
(2) Annuity Due :
(3) Deferred Annuity :
b Future Value of an Ordinary Annuity:
i) Can compute future value of an annuity by computing value to which each rent in
series will accumulate. Total their individual values. (See Illustration 6-11.)
ii)
iii) The future value of an ordinary annuity is computed as follows.
_ _ _ _ _ ( ) n,i Future value of an ordinary annuity = R FVF - OA
where: R = periodic rent; FVF-OA = future value of an ordinary annuity factor for n
periods at i interest.
iv) Example 1: What is the future value of five $5,000 deposits made at the end of each
of the next 5 years, earnings 12%?

10. Chapter 6 page 10 of 18
FV-OA = R(FVF-OA)
FV-OA =
FV-OA =
(To get the ___________ FVF-OA, look at Table 6-3, page 307. The ___% column
and the ___-period row give the FVF-OA of _________.)
v) Example 2: If we deposit $75,000 at the end of 6 months for 3 years earnings 10%
interest, what will the future value be?
FV-OA = R (FVF-OA)
FV-OA =
FV-OA =
Note: Because we are making semi-annual deposits, n =
____________________________and i =
___________________________________
(To get the ____________ FVF – OA, look at Table 6-3, page 306. Use column ____
% and row ____.)
c Future Value of an Annuity Due:
i)
ii)
iii) If rents occur at the end of a period (ordinary annuity), in determining the future value
of an annuity there will be one less interest period than if the rents occur at the
beginning of the period (annuity due).

11. Chapter 6 page 11 of 18
iv) The future value of an annuity due factor can be found by multiplying the future
value of an ordinary annuity factor by 1 plus the interest rate.
d Illustrations of Future Value of Annuity Problems:
i) Computation of Rent:
Example: You want $14,000 five years from now. You can earn a rate of 8%
compounded semiannually. How much should you deposit at the end of each 6
month period?
n =
i =
FV-OA = R (FVF-OA)
R =
R =
You must make ____ semi-annual deposits of $________.
(To get the FVF-OA factor, look at Table 6-3 on page 306. Use column ___% and
row _____.)
ii) Computation of the Number of Periodic Rents: See book page 269 to 270.
iii) Computation of the Future Value: See book page 269-270.
e Present Value of an Ordinary Annuity:
i) The present value of an annuity (PV-OA) is the single sum that, if invested at
compound interest now, would provide for an annuity (a series of withdrawals) for a
certain number of future periods. The PV-OA is the present value of a series of equal
rents to be withdrawn at equal intervals.
ii) The general formula for the present value of an ordinary annuity is as follows:
Pr _ _ _ _ _ ( ) n,i esent value of an ordinary annuity = R PVF - OA
where R = periodic rent (ordinary annuity) and PVF-OA = present value of an
ordinary annuity of $1 for n periods at i interest.
See pages 271 and 272 for example.
f Present Value of an Annuity Due:
i)

12. Chapter 6 page 12 of 18
ii) The present value of an annuity due factor can be found by multiplying the present
value of an ordinary annuity factor by 1 plus the interest rate. (For example, if we are
determining the present value of an annuity due for 5 periods at 12% interest, we can
use the present value of an ordinary annuity table to find 3.60478. Then, we multiply
this by 1.12 to get 4.03735 (the present value of an annuity due factor.) Also, you
could directly get this factor from the present value of an annuity due table (Table 6-
5.)
g Illustrations of Present Value of Annuity Problems:
i) Computation of the Present Value of an Ordinary Annuity: See text page 273-
274.
ii) Computation of the Interest Rate: See text page 274.
iii) Computation of a Periodic Rent: See text page 275.
4) More Complex Situations: Sometimes we have to use more than one table to solve one
problem.
Two common situations when we need both calculations are for deferred annuities and
bond problems.
a Deferred Annuities: An annuity in which rents begin after a specified number of
periods. Does not begin to produce rents until 2 or more periods have expired.
i) Future Value of a Deferred Annuity: Because there is no accumulation or
investment on which interest may accrue, the future value of a deferred annuity is the
same as the future value of an annuity not deferred. That is, the deferral period is
ignored in computing the future value. (See example on page 276.)
ii) Present Value of a Deferred Annuity:
(1) Must recognize the interest that accrues on the original investment during the
deferral period.
(2) To compute the present value of a deferred annuity, compute the present value of
an ordinary annuity of 1 as if the rents had occurred for the entire period, and then
subtract the present value of rents, which were not received during the deferral
period. We are left with the present value of the rents actually received
subsequent to the deferral period.
(3) Example: Sell copyright for 6 annual payments of $5,000 each. The payments
are to begin 5 years from today. Given an annual interest rate of 8%, what is the
present value of the 6 payments?

13. Chapter 6 page 13 of 18
This is an ordinary annuity of 6 payments deferred 4 periods.
Two possible solutions:
(a) Use only Table 6-4 (Present Value of an Ordinary Annuity, pages 308 and
309.)
(i) Each periodic rent $5,000
(ii) Present value of an ordinary annuity of $1
for total periods (10)
[number of rents (6) plus number of deferred
periods (4)] at 8% 6.71008
(iii) Less: Present value of an ordinary annuity
of 1 for the number of deferred periods
(4) at 8% -3.31213
(iv)Difference x 3.39795
(v) Present value of 6 rents of $5,000 deferred 4 periods $16,989.75
(b) Alternatively, the present value of the 6 rents could be computed using both
Table 6-2 (Present Value of $1, page 304 and 305) and Table 6-4.
(i) Step 1: Present Value of an ordinary annuity:
= R (PVF-OA)
=$5,000 (4.62288) (using Table 6-4)
= $23,114.40
(ii) Step 2: Present value
= FV (PVF)
= $23,114.40 (0.73503) (using Table 6-2)
= $16,989.78
b Valuation of Long-Term Bonds:
i) General:
(1) Long-term bonds produce two cash flows:
(a) Periodic interest payments during life of bond (annuity component.)
(b) Principle (face value) paid at maturity (single-sum component.)
(2) At the issuance date, bond buyers determine the present value of these two cash
flows using the market interest rate.
(3) The periodic interest payments represent an annuity, and the principal represents a
single-sum problem. The current market value of the bonds is the combined
present values of the interest annuity and the principal amount.
ii) Example 1: Assume you sold a 10-year, 10% (coupon rate) bond that has a face value
of $10,000, and pays interest semiannually. If the market rate of interest for similar
investments is also 10%, what is the selling price of your bond?
Single sum:

14. Chapter 6 page 14 of 18
Interest annuity:
Single Sum: $
Interest annuity: $
Total: $
Here, selling price = face value of the bond.
Rule: Whenever the market rate = coupon rate, the bond is sold at face value.
Journal entry at issuance:
c Effective Interest Method of Amortization of Bond Discount or Premium:
i) Premium:
ii) Discount:
iii) Accounting for premiums/discounts: Premiums/discounts are amortized (written
off) over the life of the bond issue to interest expense. The profession’s preferred
procedure for amortization of a discount or premium is the effective interest method
(also called present value amortization). Under the effective interest method:
(1) Bond interest expense is computed first by multiplying the carrying value of the
bonds at the beginning of the period by the effective interest rate.
(2) The bond discount or premium amortization is then determined by comparing the
bond interest expense with the interest to be paid.
The effective interest method produces a periodic interest expense equal to a
constant percentage of the carrying value of the bonds. Since the percentage used
is the effective rate of interest incurred by the borrower at the time of issuance,
the effective interest method results in matching expenses with revenues.
(3) See example and Illustration 6-45 on page 279!!!
iv) Example 2: Now assume you sold a 10-year, 10% (coupon rate) bond that has a face
value of $10,000, and pays interest semiannually. If the market rate of interest for
similar investments is 8%, what is the selling price of your bond?
Single sum:

15. Chapter 6 page 15 of 18
Interest annuity:
Single Sum: $
Interest Annuity: $
Total: $
Here, selling price is higher than the face value of the bond.
Rule:
Journal entry at issuance:
The bond premium can be amortized using the straight-line method or effective
interest method.
Straight-line amortization of bond premium (entry made each period for 20
periods.)
Effective interest amortization of bond premium .
Period 1:

16. Chapter 6 page 16 of 18
Period 2:
Period 3:
v) Example 3: Now assume you sold a 10-year, 10% (coupon rate) bond that has a face
value of $10,000, and pays interest semiannually. If the market rate of interest for
similar investments is 12%, what is the selling price of your bond?
Single Sum:
Interest Annuity:
Single Sum: $
Interest Annuity: $
Total: $
Here, selling price is lower than the face value of the bond.
Rule:
Journal entry at issuance:

17. Chapter 6 page 17 of 18
The bond discount can be amortized using the straight-line method or effective
interest method.
Straight-line amortization of bond discount (entry made each period for 20
periods.)
Effective interest amortization of bond discount
Period 1:
Period 2:
Period 3:
TO SUMMARIZE:

18. Chapter 6 page 18 of 18
5) Present Value Measurement:
a Choosing an Appropriate Interest Rate: Whenever you have an expected series of cash
flows, the proper interest rate must be used to discount the cash flows. The interest rate
used for this purpose has three components: (see page 280.)
i) Pure Rate of Interest (2% - 4%)
ii) Expected Inflation Rate of Interest (0% - ?)
iii) Credit Risk Rate of Interest (0% - 5%)
b Expected Cash Flow Illustration (see page 281.)