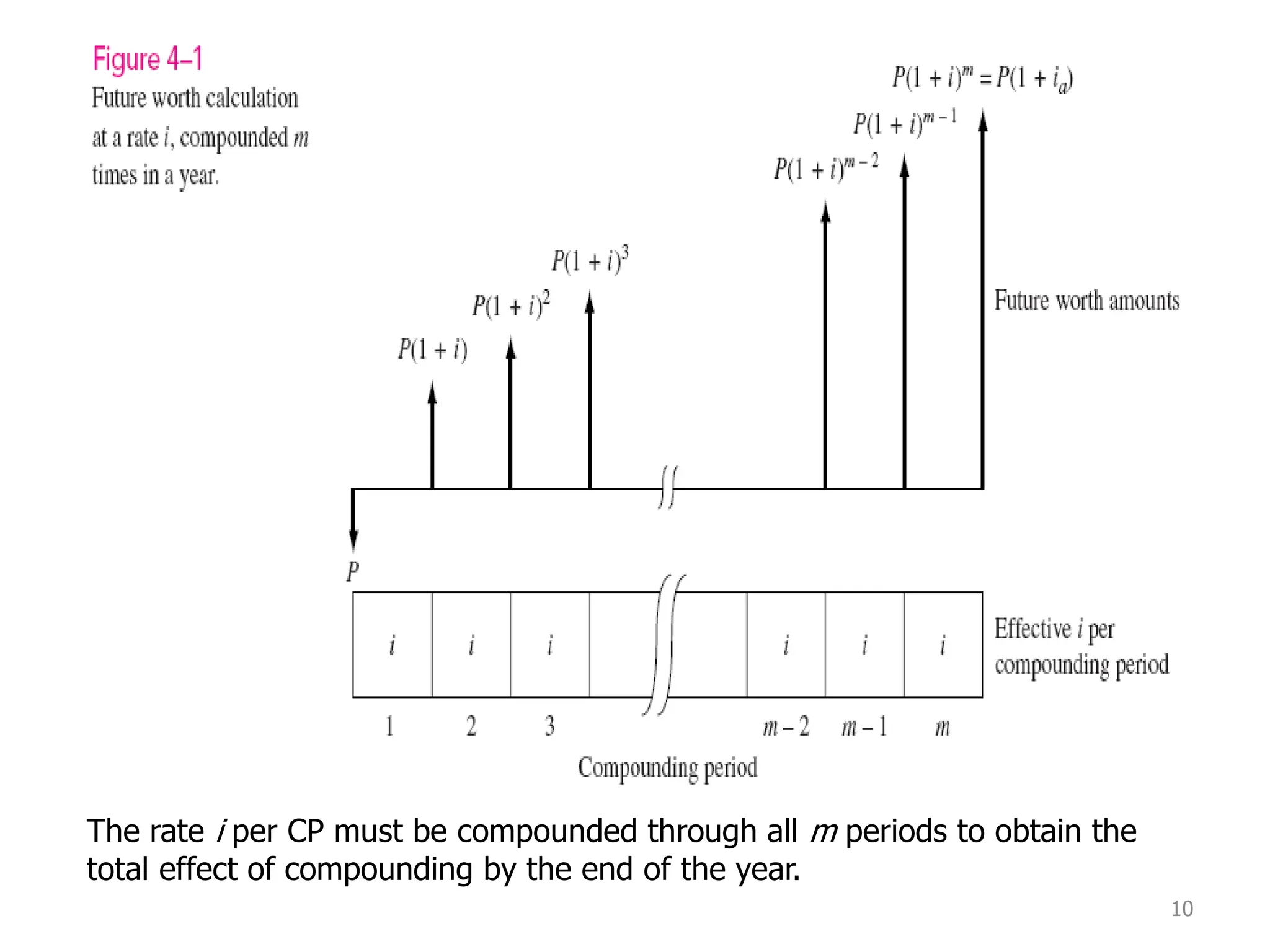
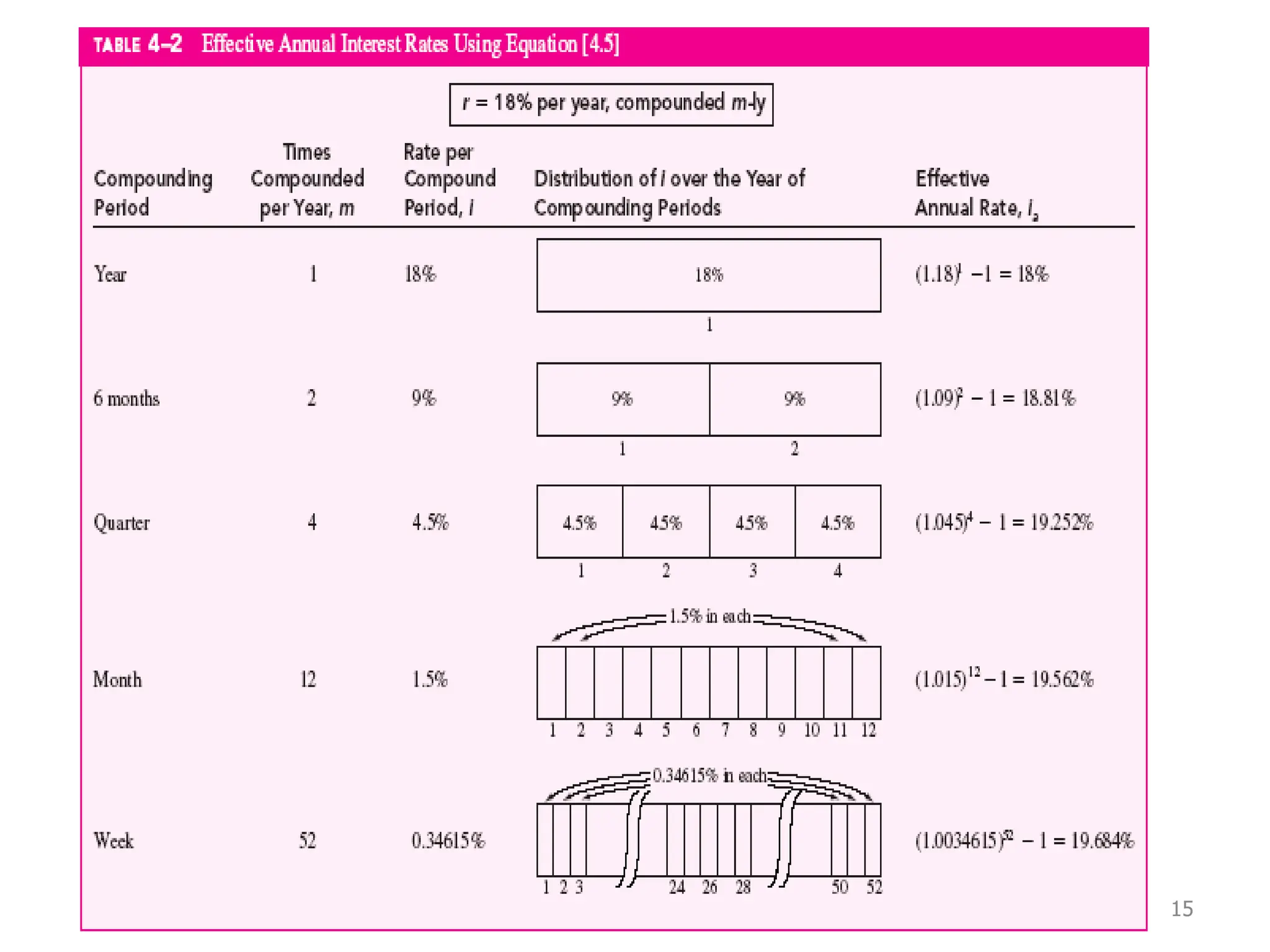
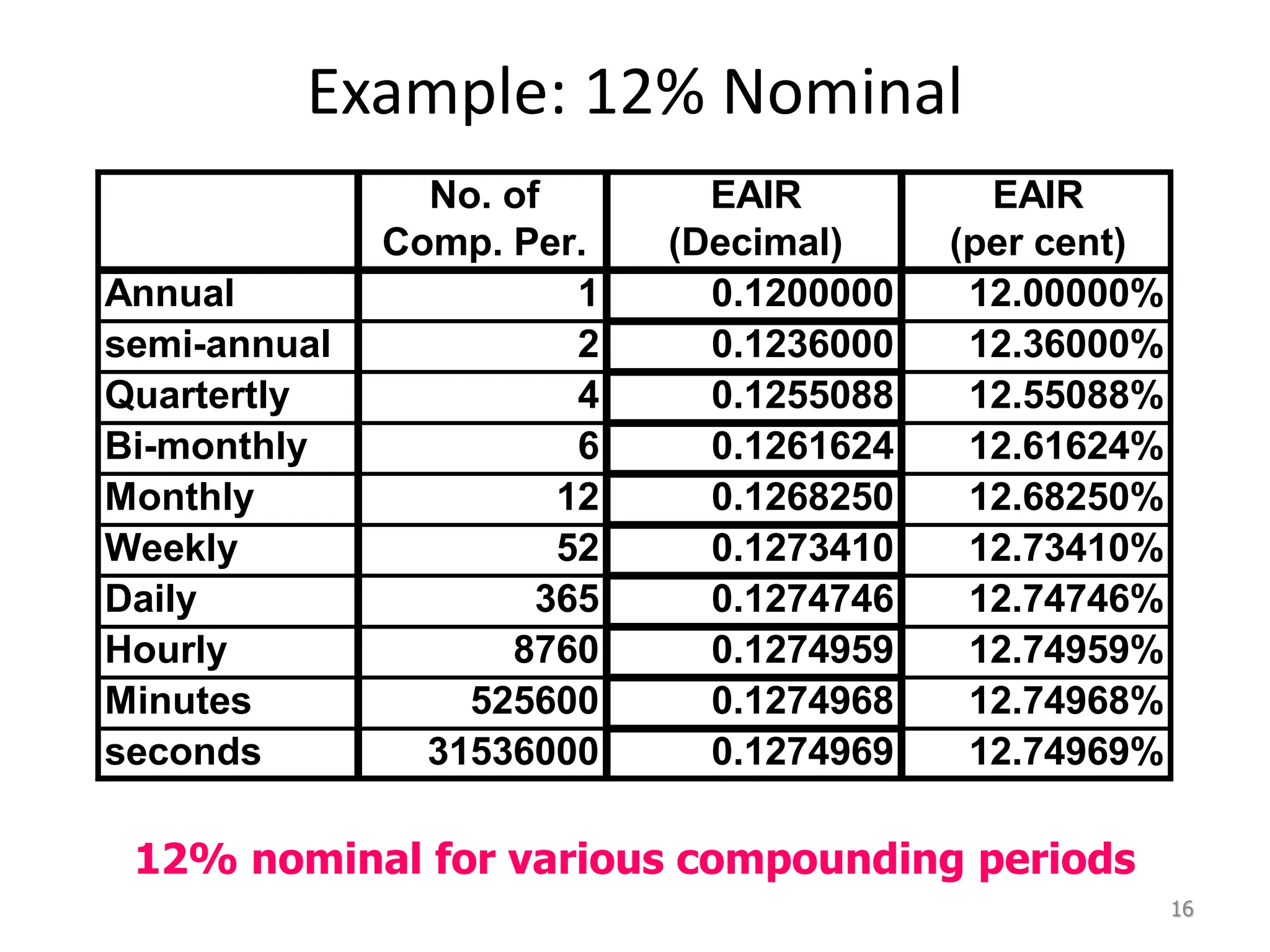
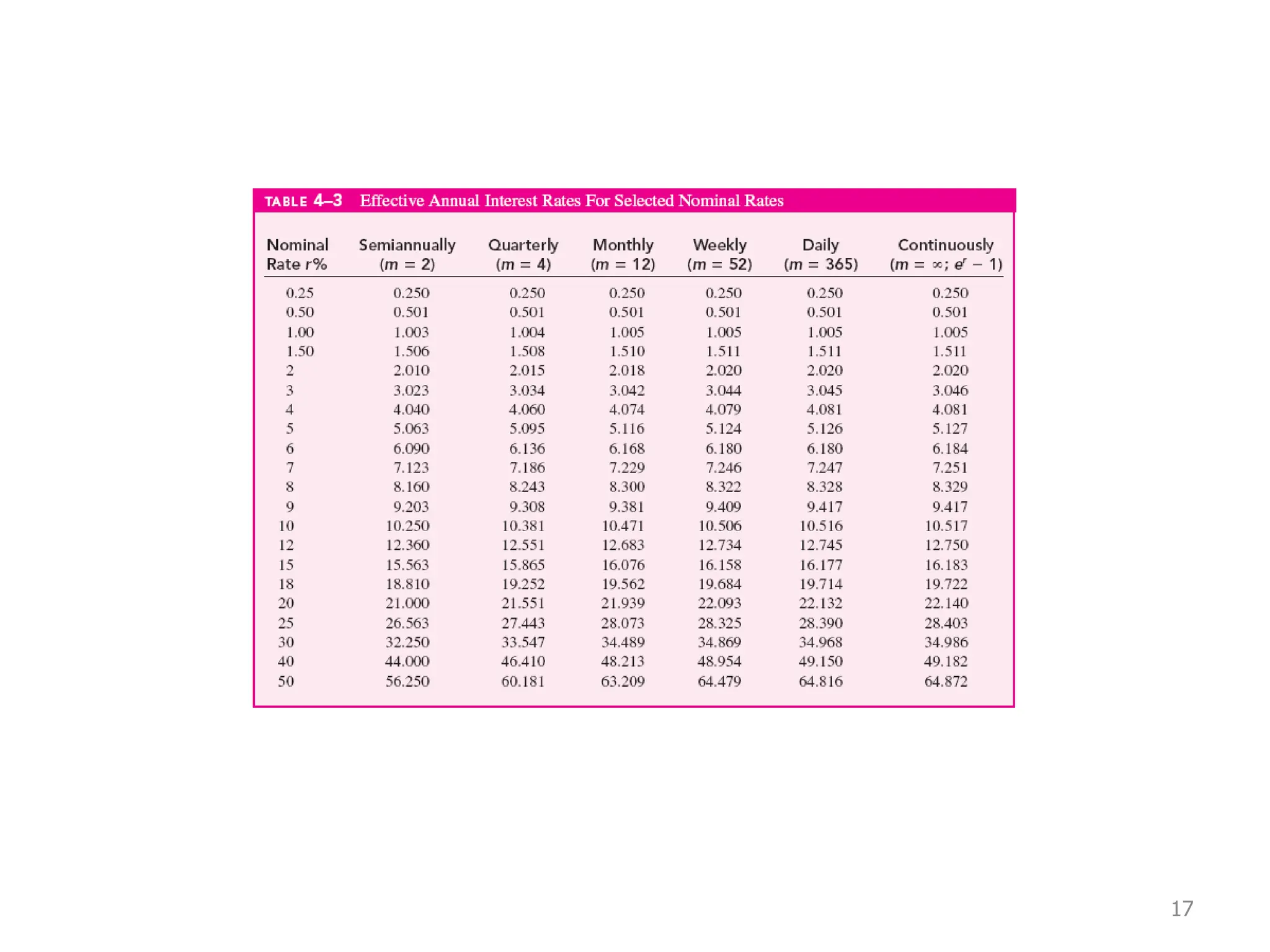
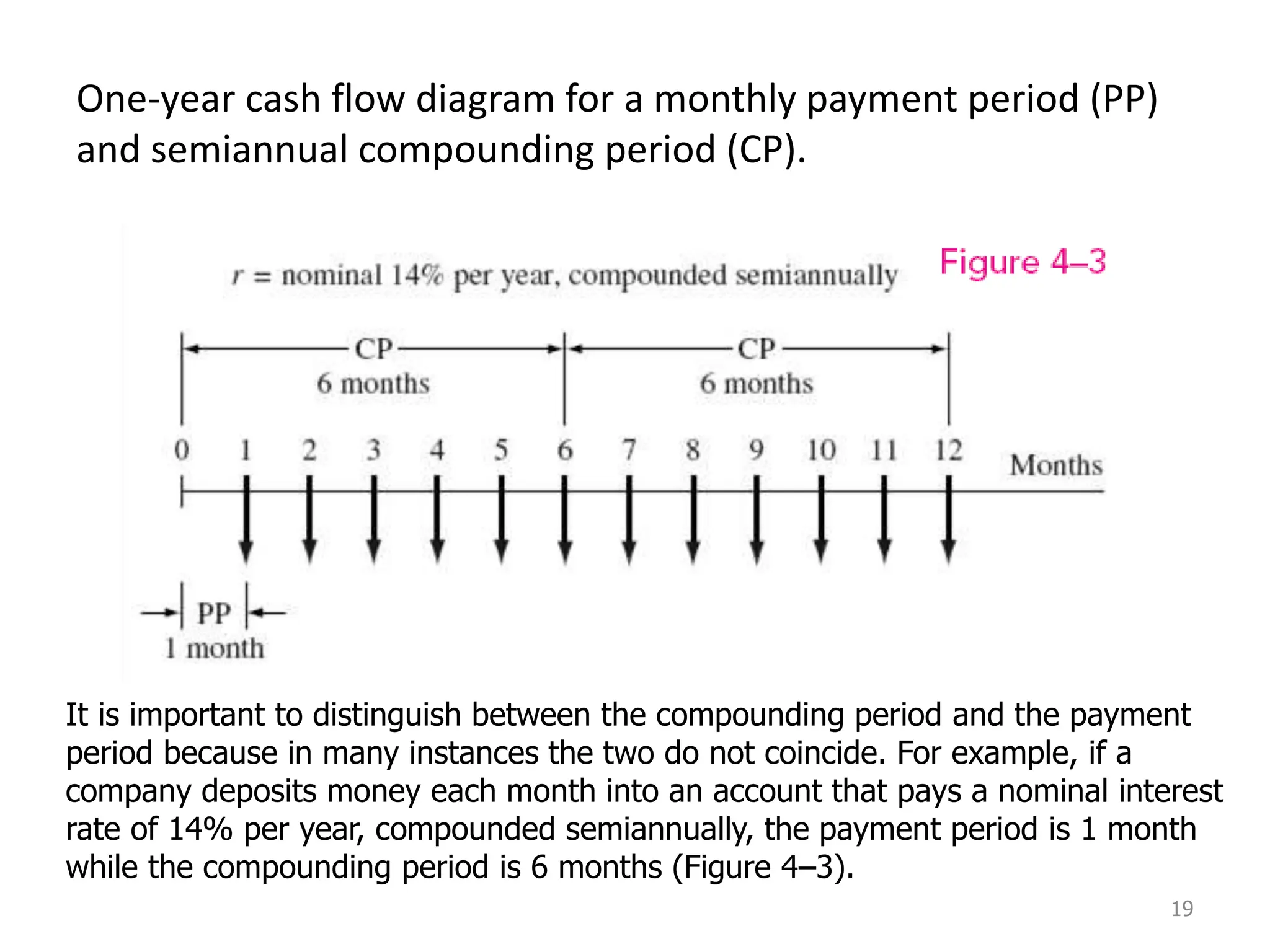
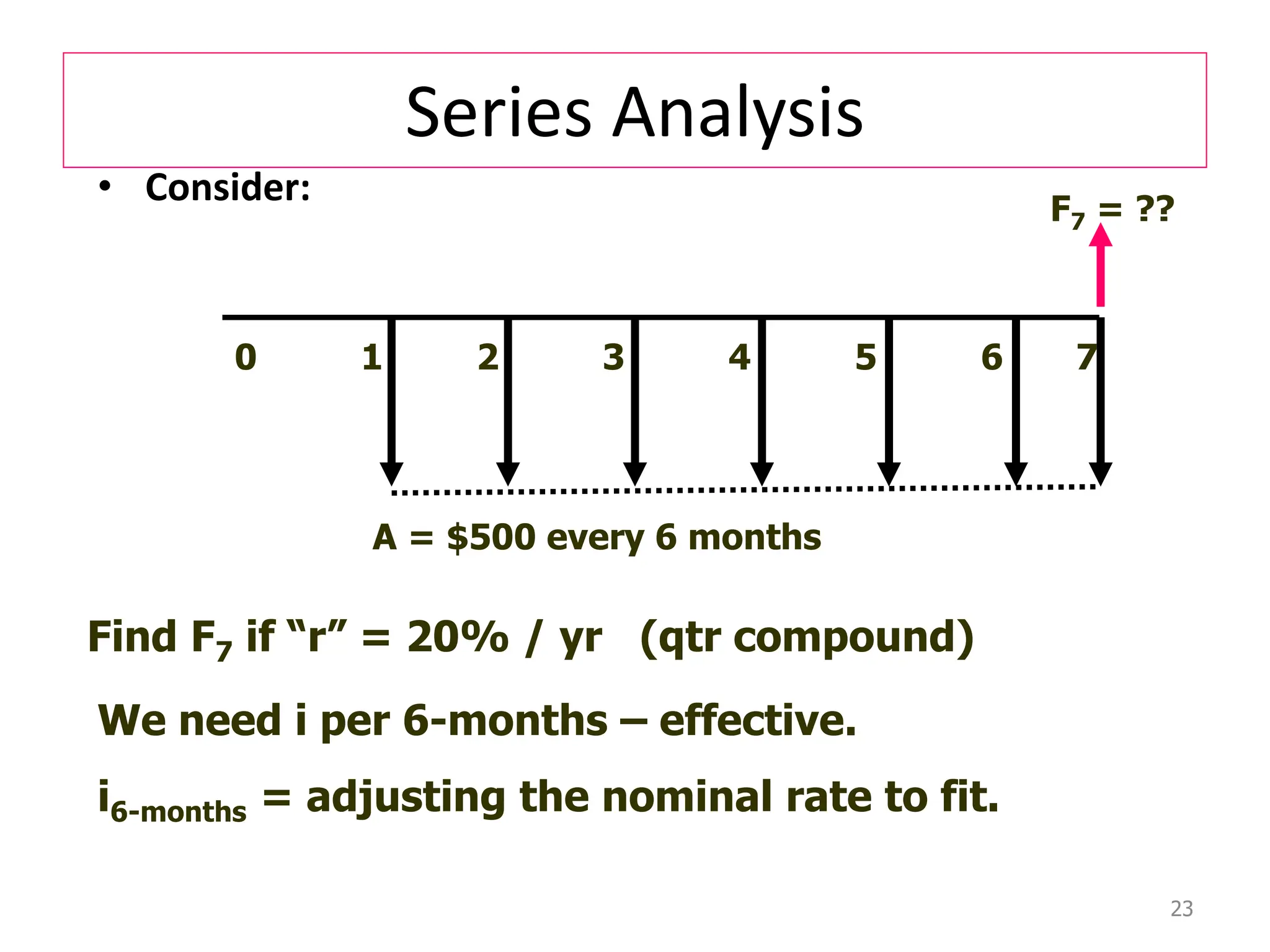
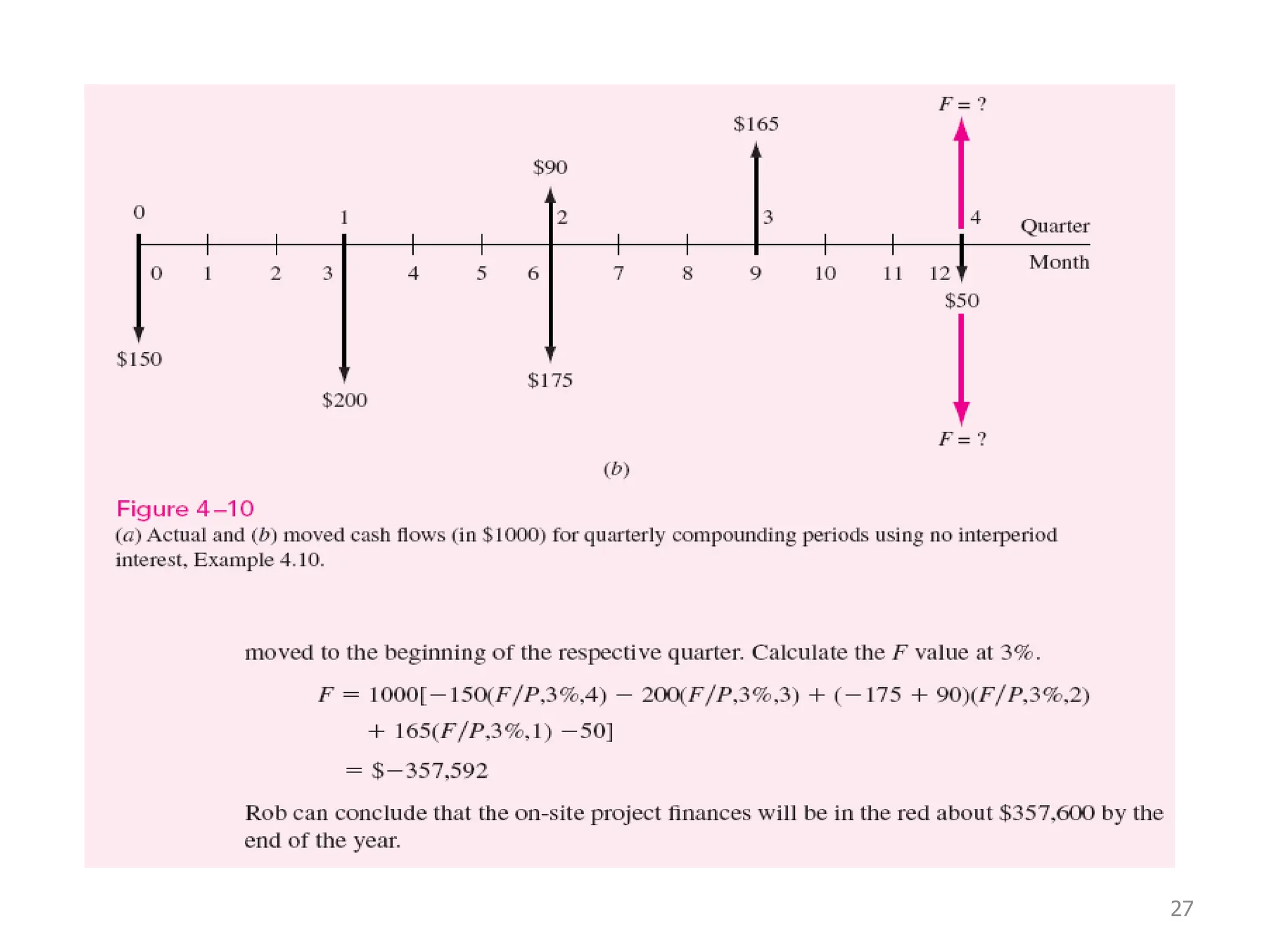
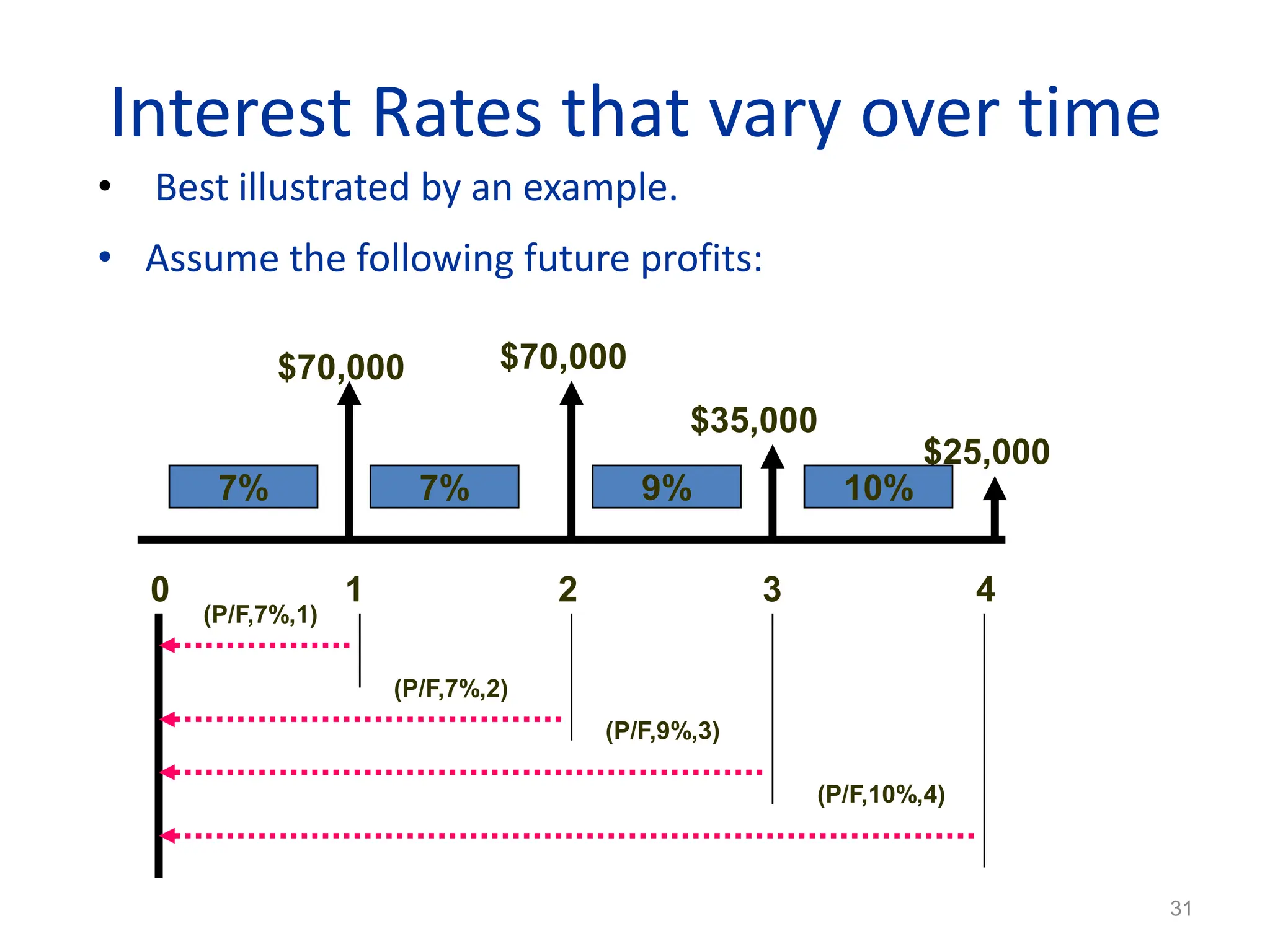
Nominal interest rates do not account for compounding, while effective interest rates do. Effective interest rates are calculated using the nominal rate and compounding period to determine the actual return. There are three key time units for any interest rate statement: the time period, compounding period, and compounding frequency. Effective rates are often higher than nominal rates due to the effects of compounding interest over time.

1. Nominal and Effective
Interest Rates
1

2. 2

3. Nominal Interest Rate
• A nominal interest rate, r, is an interest rate that does
not include any consideration of compounding
• Mathematically we have the following definition:
• r = (interest rate per period)(No. of Periods)
3

4. APR and APY
• The terms APR and APY are used in many
financial situations instead of nominal and
effective interest rates.
• The Annual Percentage Rate (APR) is the same
as the nominal interest rate, and Annual
Percentage Yield (APY) is used instead of
effective interest rate.
4

5. Examples – Nominal Interest Rates
• 1.5% per month for 24 months
– Same as: (1.5%)(24) = 36% per 24 months
• 1.5% per month for 12 months
– Same as (1.5%)(12 months) = 18% / year
• 1% per week for 1 year
– Same as: (1%)(52 weeks) = 52% per year
5

6. There are always 3 time based units associated
with an interest rate statement.
• Time period - the period over which the interest is expressed.
This is the t in the statement of r % per time period t, for
example, 1% per month. The time unit of 1 year is by far the
most common. It is assumed when not stated otherwise.
• Compounding period (CP) - the shortest time unit over which
interest is charged or earned. This is defined by the
compounding term in the interest rate statement, for
example, 8% per year compounded monthly. If not stated, it is
assumed to be 1 year.
• Compounding frequency - the number of times that m
compounding occurs within the time period t. If the
compounding period CP and the time period t are the same,
the compounding frequency is 1, for example, 1% per month
compounded monthly.
6

7. 7

8. 4.5% per 6 months – compounded weekly
• Nominal Rate: 4.5%.
• Time Period: 6 months.
• Compounded weekly:
– Assume 52 weeks per year
– 6-months then equal 52/2 = 26 weeks per 6 months
• The effective weekly rate is:
– (0.045/26) = 0.00173 = 0.173% per week
8

9. • The derivation of an effective interest rate
formula directly parallels the logic used to
develop the future worth relation:
• The future worth F at the end of 1 year is the
principal P plus the interest P(i) through the
year.
• Since interest may be compounded several
times during the year, replace i with the
effective annual rate ia and write the relation
for F at the end of 1 year.
9

10. 10
The rate i per CP must be compounded through all m periods to obtain the
total effect of compounding by the end of the year.

11. Symbols used for nominal and effective interest rates
11

12. Compound Interest – 1 Period
• Consider a one-year time period.
0 1
Invest $1 of principal at time t = 0 at
interest rate i per year.
$P = $1.00
$F=$P(1+i)1
One year later, F = P(1+i)1

13. Example: 12% per year compounded semi-annually
• i/6 month = 6%
• F1=100(1 + 0.06)=$106
• F2=$106(1 + 0.06)=$112.36 or
• 100(1 + 0.06)2 = $112.36
• To calculate ia, we can write
• 100(1+ia) = 100(1+0.12/2)2
• ia= (1+0.12/2)2 - 1=0.1236 or 12.36%
13
0
2
1
$100
112.36

14. Example: Interest is 8% per year compounded quarterly.
• What is the annual interest rate?
• Calculate: ia = (1 + 0.08/4)4 – 1
• ia = (1.02)4 – 1 = 0.0824 = 8.24% / year
• Example: “18% / year, comp. monthly”
• The effective annual rate is:
(1 + 0.18/12)12 – 1 = 0.1956 = 19.56% / year
14

15. 15

16. Example: 12% Nominal
16
No. of EAIR EAIR
Comp. Per. (Decimal) (per cent)
Annual 1 0.1200000 12.00000%
semi-annual 2 0.1236000 12.36000%
Quartertly 4 0.1255088 12.55088%
Bi-monthly 6 0.1261624 12.61624%
Monthly 12 0.1268250 12.68250%
Weekly 52 0.1273410 12.73410%
Daily 365 0.1274746 12.74746%
Hourly 8760 0.1274959 12.74959%
Minutes 525600 0.1274968 12.74968%
seconds 31536000 0.1274969 12.74969%
12% nominal for various compounding periods

17. 17

18. Equivalence: Comparing PP to CP
• CP is the “compounding period”
• PP is the “payment period”
– PP and CP’s do not always match;
– May have monthly cash flows but
compounding period is not monthly.
• Savings Accounts – for example;
– Monthly deposits with,
– Quarterly interest earned or paid;
18

19. One-year cash flow diagram for a monthly payment period (PP)
and semiannual compounding period (CP).
19
It is important to distinguish between the compounding period and the payment
period because in many instances the two do not coincide. For example, if a
company deposits money each month into an account that pays a nominal interest
rate of 14% per year, compounded semiannually, the payment period is 1 month
while the compounding period is 6 months (Figure 4–3).

20. Single Amounts: PP > CP
Example:
• r = 15%, c.m. (compounded monthly)
• Let P = $1500.00
• Find F at t = 2 years.
• 15% c.m. = 0.15/12 = 0.0125 = 1.25%/month.
• n = 2 years or 24 months
• Work in months or in years
20

21. Single Amounts: PP > CP*
• Approach 1. (work with months)
– F24 = $1,500(F/P,0.15/12,24);
– F24 = $1,500(F/P,1.25%,24);
– F24 = $1,500(1.0125)24 = $2,021.03.
• Approach 2. (work with years)
– Assume n = 2 years and i/month =0.0125
– Eff i = (1.0125)12 – 1 = 0.1608 (16.08%)
– F2 = $1,500(F/P,16.08%,2)
– F2 = $1,500(1.1608)2 = $2,021.30.
21

22. 22

23. Series Analysis
• Consider:
23
0 1 2 3 4 5 6 7
A = $500 every 6 months
F7 = ??
Find F7 if “r” = 20% / yr (qtr compound)
We need i per 6-months – effective.
i6-months = adjusting the nominal rate to fit.

24. Series Example
• Adjusting the interest
• r = 20% (qtr compound)
• i/qtr. = 0.20/4 = 0.05 = 5%/qtr.
• 2-qtrs in a 6-month period.
• i6-months = (1.05)2 – 1 = 10.25%/6-months.
• Now, the interest matches the payments.
• Fyear 7 = Fperiod 14 = $500(F/A,10.25%,14)
• F = $500(28.4891) = $14,244.50
24

25. Single Amounts/Series with PP < CP
• Consider a one-year cash flow situation.
• Payments are made at end of a given month.
• Interest rate is r = 12% / yr, compound qtr.
25

26. 26

27. 27

28. Continuous Compounding
• Example:
• What is the effective annual interest rate if the
nominal rate is given as:
– r = 18%, compounded continuously
28
Solve e0.18 – 1 = 1.1972 – 1 = 19.72% / year
The 19.72% represents the MAXIMUM effective
annual interest rate for 18% compounded.

29. Example
• An investor requires an effective return of at least 15%
per year. What is the minimum annual nominal rate that
is acceptable if interest on his investment is compounded
continuously?
• Solution:
er – 1 = 0.15
er = 1.15
ln(er) = ln(1.15)
r = ln(1.15) = 0.1398 = 13.98%
29

30. Interest Rates that vary over time
• In practice – interest rates do not stay the same over
time unless stipulated in a contract.
• There can exist “variation” of interest rates over time –
30

31. Interest Rates that vary over time
• Best illustrated by an example.
• Assume the following future profits:
31
0 1 2 3 4
$70,000 $70,000
$35,000
$25,000
7% 7% 9% 10%
(P/F,7%,1)
(P/F,7%,2)
(P/F,9%,3)
(P/F,10%,4)

32. Period-by-Period Analysis
• P0 =
1. $70000(P/F,7%,1)
2. $70000(P/F,7%,1)(P/F,7%,1)
3. $35000(P/F,9%,1)(P/F,7%,1)2
4. $25000(P/F,10%,1)(P/F,9%,1)(P/F,7%,1)2
32
P: $172,816 at t = 0…

33. Varying Rates: Approximation
• An alternative approach that approximates the
present value:
• Average the interest rates over the appropriate
number of time periods.
• Example:
– {7% + 7% + 9% + 10%}/4 = 8.25%;
– Work the problem with an 8.25% rate;
– Merely an approximation.
33

34. • Since many real-world situations involve cash flow
frequencies and compounding periods other than 1 year,
it is necessary to use nominal and effective interest rates.
• When a nominal rate r is stated, the effective interest
rate per payment period is determined by using the
effective interest rate equation. However, when series
cash flows (A, G, and g) are present, only one
combination of the effective rate i and number of periods
n is correct for the factors.
• This requires that the relative lengths of PP and CP be
considered as i and n are determined. The interest rate
and payment periods must have the same time unit for
the factors to correctly account for the time value of
money.
34

35. 35