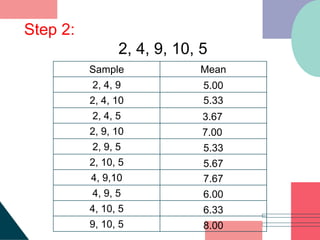
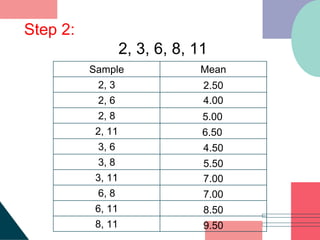
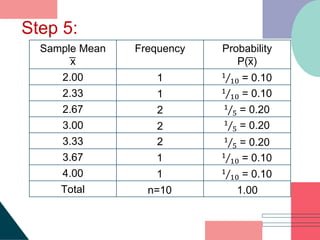
1. The document describes how to construct a sampling distribution of sample means from a population. It provides steps to list all possible samples, compute the mean of each sample, and construct a frequency distribution of the sample means. 2. It also gives steps to find the mean and variance of the sampling distribution, which includes computing the population mean and variance, determining possible samples, computing sample means, and calculating the mean and variance of the sampling distribution. 3. Examples are provided to demonstrate constructing sampling distributions of sample means and finding the mean and variance of the distributions using populations with different sample sizes.

3. 1. I will be flashing an empty boxes
representing to the term or phrase/s
that you are trying to guess.
2. Everyone can have a chance to tell
a letter or guess the answer.
3. Click the raise hand button if you
want to give letter but, if you know the
answer type it in the chat box.
Mechanics:

4. 4. If you guess correctly, letters will be
revealed in the boxes but, if you
guess incorrectly, letters will not be
revealed.
5. The first 5 students who get the
correct answer each number will
have an additional points for the
activity.
Mechanics:

5. A B C D E F G H I J K L M N O P
Q R S T U V W X Y Z
A
A
A
A
A
B
B
B
B
B C
C
C
C
C D
D
D
D
D E
E
E
E
E F
F
F
F
F G
G
G
G
G
H
H
H
H
H I
I
I
I
I
J
J
J
J
J K
K
K
K
K L
L
L
L
L
M
M
M
M
M
N
N
N
N
N
O
O
O
O
O P
P
P
P
P
Q
Q
Q
Q
Q R
R
R
R
R S
S
S
S
S
T
T
T
T
T U
U
U
U
U V
V
V
V
V W
W
W
W
W X
X
X
X
X Y
Y
Y
Y
Y Z
Z
Z
Z
Z
REVEAL

6. A B C D E F G H I J K L M N O P
Q R S T U V W X Y Z
A
A
A
A
A
B
B
B
B
B C
C
C
C
C
D
D
D
D
D E
E
E
E
E
F
F
F
F
F G
G
G
G
G H
H
H
H
H I
I
I
I
I
J
J
J
J
J K
K
K
K
K L
L
L
L
L M
M
M
M
M
N
N
N
N
N
O
O
O
O
O P
P
P
P
P Q
Q
Q
Q
Q R
R
R
R
R
S
S
S
S
S T
T
T
T
T U
U
U
U
U V
V
V
V
V
W
W
W
W
W X
X
X
X
X Y
Y
Y
Y
Y Z
Z
Z
Z
Z
REVEAL

7. A B C D E F G H I J K L M N O P
Q R S T U V W X Y Z
A
A
A
A
A B
B
B
B
B C
C
C
C
C
D
D
D
D
D E
E
E
E
E
F
F
F
F
F
G
G
G
G
G H
H
H
H
H I
I
I
I
I J
J
J
J
J K
K
K
K
K L
L
L
L
L M
M
M
M
M
N
N
N
N
N
O
O
O
O
O P
P
P
P
P Q
Q
Q
Q
Q
R
R
R
R
R
S
S
S
S
S T
T
T
T
T U
U
U
U
U
V
V
V
V
V W
W
W
W
W X
X
X
X
X Y
Y
Y
Y
Y
Z
Z
Z
Z
Z
REVEAL

8. A B C D E F G H I J K L M N O P
Q R S T U V W X Y Z
A
A
A
A
A
B
B
B
B
B C
C
C
C
C D
D
D
D
D E
E
E
E
E
F
F
F
F
F G
G
G
G
G H
H
H
H
H I
I
I
I
I J
J
J
J
J K
K
K
K
K L
L
L
L
L
M
M
M
M
M
N
N
N
N
N
O
O
O
O
O P
P
P
P
P
Q
Q
Q
Q
Q R
R
R
R
R S
S
S
S
S
T
T
T
T
T U
U
U
U
U V
V
V
V
V W
W
W
W
W X
X
X
X
X Y
Y
Y
Y
Y Z
Z
Z
Z
Z
REVEAL

9. A B C D E F G H I J K L M N O P
Q R S T U V W X Y Z
A
A
A
A
A
B
B
B
B
B
C
C
C
C
C D
D
D
D
D E
E
E
E
E F
F
F
F
F G
G
G
G
G H
H
H
H
H I
I
I
I
I
J
J
J
J
J K
K
K
K
K L
L
L
L
L
M
M
M
M
M
N
N
N
N
N O
O
O
O
O
P
P
P
P
P
Q
Q
Q
Q
Q R
R
R
R
R
S
S
S
S
S T
T
T
T
T
U
U
U
U
U V
V
V
V
V W
W
W
W
W X
X
X
X
X Y
Y
Y
Y
Y
Z
Z
Z
Z
Z
REVEAL

10. Sampling and
Sampling Distribution
Prepared by:
Marivic Pareja

11. 1.Construct sampling distribution of
sample mean;
2.Find the mean and variance of the
sampling distribution of the sample
mean;
3.Solve problems involving sampling
distribution of the sample means.
Objectives:
At the end of the lesson, students should
be able to:

12. Sampling Distribution of
Sample Means
A sampling distribution of sample means is
a frequency distribution using the means
computed from all possible random samples of
a specific size taken from a population.

13. Steps in Constructing the
Sampling Distribution of
Sample Means
1. Determine the number of possible samples
that can be drawn from the population using
the formula:
NCn=
𝐍!
𝐧! 𝐍−𝐧 !
where:
N= size of the population
n= size of the sample

14. Steps in Constructing the
Sampling Distribution of
Sample Means
2. List all the possible samples and compute
the mean of each sample.
3. Construct the sampling distribution of the
sample means.
4. Draw a histogram of the sampling
distribution of the means.

15. A population consists of the numbers 2, 4,
9, 10, and 5. Let us list all possible samples of
size 3 from this population and compute the mean
of each sample.
Step1:
NCn=
𝐍!
𝐧! 𝐍−𝐧 !
=
𝟓!
𝟑! 𝟓−𝟑 !
=
𝟓!
𝟑!∗𝟐!
=
𝟓∗𝟒∗𝟑!
𝟑!∗𝟐!
=
𝟓∗𝟒
𝟐∗𝟏
=
𝟐𝟎
𝟐
= 10
where: N= 5 n=3
Example 1:
There are 10 possible samples of size 3 that can be
drawn from the given population.

16. Step 2:
2, 4, 9, 10, 5
Sample Mean
2, 4, 9
2, 4, 10
2, 4, 5
2, 9, 10
2, 9, 5
2, 10, 5
4, 9,10
4, 9, 5
4, 10, 5
9, 10, 5
5.00
5.33
3.67
7.00
5.33
5.67
7.67
6.00
6.33
8.00

17. Step 3:
Sample Mean
͞x
Frequency Probability
P(͞x)
3.67
5.00
5.33
5.67
6.00
6.33
7.00
7.67
8.00
Total n=10
1
1
1
1
1
1
2
1
1 1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
2
10 = 0.20
1.00
Sample Mean
2, 4, 9 5.00
2, 4, 10 5.33
2, 4, 5 3.67
2, 9, 10 7.00
2, 9, 5 5.33
2, 10, 5 5.67
4, 9,10 7.67
4, 9, 5 6.00
4, 10, 5 6.33
9, 10, 5 8.00

18. Step 4:
0
0.05
0.1
0.15
0.2
0.25
3.67 5 5.33 5.67 6 6.33 7 7.67 8

19. Step 1:
NCn=
𝐍!
𝐧! 𝐍−𝐧 !
=
𝟓!
𝟐! 𝟓−𝟐 !
=
𝟓∗𝟒∗𝟑!
𝟐!∗𝟑!
=
𝟓∗𝟒
𝟐∗𝟏
=
𝟐𝟎
𝟐
= 10
Example 2:
A population consists of five numbers 2, 3, 6, 8, and 11.
Consider samples of size 2 that can be drawn from this
population.
There are 10 possible
samples of size 2 that can
be drawn from the given
population.

20. Step 2:
2, 3, 6, 8, 11
Sample Mean
2, 3
2, 6
2, 8
2, 11
3, 6
3, 8
3, 11
6, 8
6, 11
8, 11
2.50
4.00
5.00
6.50
4.50
5.50
7.00
7.00
8.50
9.50

21. Step 3:
Sample Mean
͞x
Frequency Probability
P(͞x)
2.50
4.00
4.50
5.00
5.50
6.50
7.00
8.50
9.50
Total n=10
1
1
2
1
1
1
1
1
1 1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
2
10 = 0.20
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1
10 = 0.10
1.00

22. Step 4:
0
0.05
0.1
0.15
0.2
0.25
2.5 4 4.5 5 5.5 6.5 7 8.5 9.5

23. Finding the Mean and
Variance of the Sampling
Distribution of Means

24. Steps in Finding the Mean and
Variance of Sampling Distribution
of Sample Means
1.Compute the mean of the population (µ).
2.Compute the variance of the population (σ).
3.Determine the number of possible samples.
4.List all possible samples and their
corresponding means.
5.Construct the sampling distribution of the
sample means.

25. Steps in Finding the Mean and
Variance of Sampling Distribution
of Sample Means
6. Compute the mean of the sampling
distribution of the sample means.
7. Compute the variance of the sampling
distribution of the sample means.
8. Construct the histogram for the sampling
distribution of the sample means.

26. Step 1:
µ =
X
N
=
1+2+3+4+5
5
=
15
5
`
= 3
Example 1: Consider a population consisting of 1,
2, 3, 4, and 5. Suppose samples of size 2 are drawn
from this population.

27. Step 2:
x X-µ (x-µ)²
1
2
3
4
5
-2
4
2
1
0
-1
4
0
1
1
𝑥 − 𝜇 2
= 10
σ² =
(x−μ)²
N
=
10
5
= 2

28. NCn=
𝐍!
𝐧! 𝐍−𝐧 !
=
𝟓!
𝟐! 𝟓−𝟐 !
=
𝟓∗𝟒∗𝟑!
𝟐!∗𝟑!
=
𝟓∗𝟒
𝟐∗𝟏
=
𝟐𝟎
𝟐
= 10
Step 3:
Where:
N=5
n=2

29. Step 4:
1, 2, 3, 4, 5
Sample Mean
1, 2
1, 3
1, 4
1, 5
2, 3
2, 4
2, 5
3, 4
3, 5
4, 5
1.50
2.00
2.50
3.00
2.50
3.00
3.50
3.50
4.00
4.50

30. Step 5:
Sample Mean
͞x
Frequency Probability
P(͞x)
1.50
2.00
2.50
3.00
3.50
4.00
4.50
Total n=10
1
1
2
2
2
1
1 1
10 = 0.10
1
10 = 0.10
1
5 = 0.20
1
5 = 0.20
1
10 = 0.10
1
10 = 0.10
1
5 = 0.20
1.00

31. Step 6:
Sample Mean
͞x
Probability
P(͞x)
͞x●P(͞x)
1.50
2.00
2.50
3.00
3.50
4.00
4.50
Total 1.00
1
10
1
10
1
5
1
5
1
5
1
10
1
10 0.15
0.45
0.60
0.70
0.40
0.20
0.50
3.00
µ𝑥 =͞x●P(͞x)
=3.00

32. Step 7:
͞x P(͞x) ͞x-µ (͞x-µ)² P(͞x)●(͞x-µ)²
Total
1.50
0.100
4.50
4.00
3.50
3.00
2.50
2.00
1
10
1
10
1
10
1
10
1
5
1
5
1
5
1.00
2.25
1.50
1.00
0.50
0.00
-1.50
-1.00
-0.50
2.25
1.00
0.25
0.00
0.25
0.225
0.225
0.100
0.050
0.050
0.000
1.00 0.75

33. Step 7:
σ²= P(͞x)●(͞x-µ)²
=0.75

34. Step 8:
0
0.05
0.1
0.15
0.2
0.25
1.5 2 2.5 3 3.5 4 4.5
Sample Mean
Probability

35. Step 1:
µ =
X
N
=
1+2+3+4+5
5
=
15
5
`
= 3
Example 2: Consider a population consisting of 1,
2, 3, 4, and 5. Suppose samples of size 3 are drawn
from this population.

36. Step 2:
x X-µ (x-µ)²
1
2
3
4
5
-2
4
2
1
0
-1
4
0
1
1
𝑥 − 𝜇 2
= 10
σ² =
(x−μ)²
N
=
10
5
= 2

37. NCn=
𝐍!
𝐧! 𝐍−𝐧 !
=
𝟓!
𝟑! 𝟓−𝟑 !
=
𝟓∗𝟒∗𝟑!
𝟑!∗𝟐!
=
𝟓∗𝟒
𝟐∗𝟏
=
𝟐𝟎
𝟐
= 10
Step 3:
Where:
N=5
n=3

38. Step 4:
1, 2, 3, 4, 5
Sample Mean
1, 2, 3
1, 2, 4
1, 2, 5
1, 3, 4
1, 3, 5
1, 4, 5
2, 3, 4
2, 3, 5
2, 4, 5
3, 4, 5
2.00
2.33
2.67
2.67
3.00
3.33
3.00
3.33
3.67
4.00

39. Step 5:
Sample Mean
͞x
Frequency Probability
P(͞x)
2.00
2.33
2.67
3.00
3.33
3.67
4.00
Total n=10
1
1
2
2
2
1
1 1
10 = 0.10
1
10 = 0.10
1
5 = 0.20
1
5 = 0.20
1
10 = 0.10
1
10 = 0.10
1
5 = 0.20
1.00

40. Step 6:
Sample Mean
͞x
Probability
P(͞x)
͞x●P(͞x)
2.00
2.33
2.67
3.00
3.33
3.67
4.00
Total 1.00
1
10
1
10
1
5
1
5
1
5
1
10
1
10 0.20
0.40
0.60
0.67
0.37
0.23
0.53
3.00
µ𝑥 =͞x●P(͞x)
=3.00

41. Step 7:
͞x P(͞x) ͞x-µ (͞x-µ)² P(͞x)●(͞x-µ)²
Total
2.00
0.045
4.00
3.67
3.33
3.00
2.67
2.33
1
10
1
10
1
10
1
10
1
5
1
5
1
5
0.45
1.00
1.00
0.67
0.33
0.00
-1.00
-0.67
-0.33
1.00
0.45
0.11
0.00
0.11
0.100
0.100
0.045
0.020
0.020
0.000
1.00 0.33

42. Step 7:
σ²= P(͞x)●(͞x-µ)²
=0.33

43. Step 8:
0
0.05
0.1
0.15
0.2
0.25
2 2.33 2.67 3 3.33 3.67 4
Sample Mean
Probability

44. Solving Problems
Involving Sampling
Distribution of the Sample
Means

45. Z=
𝑥−µ
σ
Z=
𝑥−µ
σ
√𝑛
where:
͞x=Sample mean
x=Given Measurement
µ=Population mean
σ=Population standard deviation
n=Sample size
Formulas:

46. a. What is the probability that a randomly selected
college student will complete the examination in less
than 43 minutes?
Step 1: Identify the given information
µ= 46.2
σ= 8
x= 43

47. Step 2: Identify what is being asked for.
P(x<43)
Step 3: Identify the formula to be used.
Z=
𝑥−µ
σ

48. Step 4: Solve the problem.
z=
𝑥−µ
σ
z=
43−46.2
8
z=
−3.2
8
z=-0.40

49. Step 4: Solve the problem.
P(x<43) = P(z<-0.40)
= 0.5000-0.1554
= 0.3446 or 34.36%
-3 -2 -1 0 1 2 3
z=-0.40 0.1554

50. Step 5: State the final answer.
Therefore, the probability that a randomly
selected college student will complete the
examination in less than 43 minutes is 0.3446
or 34.46%.

51. b.If 50 randomly selected college students take the
examination, what is the probability that the mean time
it takes the group to complete the test will be less than
43 minutes?
Step 1: Identify the given information
µ= 46.2 ͞x=43
σ= 8 n=50

52. Step 2: Identify what is being asked for.
P(͞x<43)
Step 3: Identify the formula to be used.
Z=
𝑥−µ
σ
√𝑛

53. Step 4: Solve the problem.
Z=
𝑥−µ
σ
√𝑛
=
43−46.2
8
√50
=
−3.2
8
√50
= -2.83

54. Step 4: Solve the problem.
P(͞x<43) = P(z<-2.83)
= 0.5000-0.4977
= 0.0023 or 0.23%
-3 -2 -1 0 1 2 3
z=-2.83  0.4977

55. Step 5: State the final answer.
Therefore, the probability that 50 randomly
selected college student will complete the
examination in less than 43 minutes is 0.0023
or 0.23%.

56. a.If cup of ice cream is selected, what is the probability
that the cholesterol content will be more than 670 mg?
Step 1: Identify the given information
µ= 660
σ= 35
x=670

57. Step 2: Identify what is being asked for.
P(x>670)
Step 3: Identify the formula to be used.
Z=
𝑥−µ
σ

58. Step 4: Solve the problem.
Z=
𝑥−µ
σ
=
670−660
35
=
10
35
=0.29

59. Step 4: Solve the problem.
P(x>670) = P(z>0.29)
= 0.5000-0.1141
= 0.3859 or 38.59%
-3 -2 -1 0 1 2 3
z=0.29 0.1141

60. Step 5: State the final answer.
Therefore, the probability that the
cholesterol content will be more than 670 mg is
0.3859 or 38.59%.

61. b.If a sample of 10 cups of ice cream is selected, what
is the probability that the mean of the sample will be
larger than 670 mg?
Step 1: Identify the given information
µ= 660 ͞x=670
σ= 35 n=10

62. Step 2: Identify what is being asked for.
P(͞x>670)
Step 3: Identify the formula to be used.
Z=
𝑥−µ
σ
√𝑛

63. Step 4: Solve the problem.
Z=
𝑥−µ
σ
√𝑛
=
670−660
35
√10
=
10
35
√10
= 0.90

64. Step 4: Solve the problem.
P(͞x>670) = P(z>0.90)
= 0.5000-0.3159
= 0.1841 or 18.41%
-3 -2 -1 0 1 2 3
z=0.90 0.3159

65. Step 5: State the final answer.
Therefore, the probability that the mean
cholesterol content of 10 randomly selected
cups of ice cream will be more than 670 mg is
0.1841 or 18.41%.