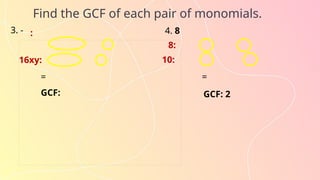
The document is an introduction to factoring polynomials, emphasizing its importance in understanding algebraic expressions and solving polynomial equations. It outlines key concepts including definitions, examples, and step-by-step processes for factoring various types of polynomials. Additionally, it covers techniques for identifying common factors and factoring higher-order polynomials, enhancing students' mathematical skills applicable in real-world scenarios.

1. Welcome to Mathematics
Class!
by Kayra Theress Gubat

2. Welcome to Mathematics
Class!
by Kayra Theress Gubat

3. Introduction to Factoring
Polynomials
Factoring polynomials is a fundamental
skill in mathematics that allows us to break
down complex algebraic expressions into
simpler, more manageable forms. By
mastering the art of factoring, students
gain a deeper understanding of polynomial
functions, which are essential in fields
ranging from physics and engineering to
economics and beyond.
by Kayra Theress Gubat

4. What is a Polynomial?
1 Definition
A polynomial is an algebraic expression that consists of
one or more terms, each of which is a product of a
constant and one or more variables raised to a non-
negative integer power.
2 Examples
Common examples of polynomials include linear
expressions (e.g., 3x + 2), quadratic expressions (e.g., ),
and cubic expressions (e.g., ).
3 Importance
Polynomials are ubiquitous in mathematics and have
countless real-world applications, making them a crucial
topic for students to master.

5. Importance of Factoring Polynomials
Simplification
Factoring polynomials
can help simplify complex
expressions, making
them easier to work with
and understand. By
breaking down a
polynomial into its
component factors,
students can more easily
identify patterns and
relationships within the
expression.
Problem Solving
Factoring is a crucial step
in solving many types of
polynomial equations
and inequalities. By
factoring the polynomial,
students can more easily
find the roots or solutions
to the equation, which is
essential in various
mathematical
applications.
Conceptual
Understanding
The process of factoring
polynomials helps
students develop a
deeper understanding of
the structure and
properties of polynomial
functions. This
knowledge is crucial for
success in more
advanced mathematics
courses and real-world
problem-solving.

6. Common Monomial Factors
1 Coefficient
The numerical factor, or coefficient, of a monomial is
the first thing to look for when identifying common
factors. For example, in the expression , the common
coefficient are 6 and 3.
2 Variable
The variable factors, or powers of the variables, must also
be examined to find common factors. In the expression ,
the common variable factor is x and y.
3 Exponent
The exponents of the variables are also important when
identifying common factors. For instance, in the
expression , the common exponent are 4 and 2.

7. Identifying Common Monomial
Factors
1 Step 1
Examine the coefficients of the
monomials to find the largest common
factor.
2 Step 2
Identify the common variables and their
corresponding exponents in the
monomials.
3 Step 3
Combine the common coefficient and
variable factors to form the greatest
common monomial factor.

8. 10
18 :

9. 4
10
12:

10. Welcome to Mathematics
Class!
by Kayra Theress Gubat

11. Factoring Polynomials
with Common Monomial
Factors
by Kayra Theress Gubat

12. Objectives:
1 Find the greatest
common factor (GCF) by
listing or prime
factorization
2 Factor polynomials
completely with common
monomial factor; and
3 Use distributive property
to factor polynomials.

13. Unlocking Words Difficulty
 Greatest Common Factor (GCF)
 Prime Factors
 Monomial
 Polynomial
 Standard Form

14. Greatest Common Factor (GCF)
- Refers to the common factor
having the greatest numerical
factor and with variables having
the least degree.
Example:
6:
15:
1, 2, 3, 6,
1, 3, 5, 15,
GCF:
6:
15:
(2) · (3) · ()
(3) · (5) · ()
GCF:

15. Welcome to Mathematics
Class!
by Kayra Theress Gubat

16. Find the GCF of each pair of monomials.
6:
1. 6
18:
=
GCF:
2. 10
10:
12:
=
GCF: 2

17. Find the GCF of each pair of monomials.
:
3. -
16xy:
=
GCF:
4. 8
8:
10:
=
GCF: 2

18. FACTORING POLYNOMIAL
- rewriting a polynomial as a
product of polynomials of
smaller degree.
POLYNOMIAL GCF FACTORED
FORM

19. FACTORING POLYNOMIAL
- rewriting a polynomial as a
product of polynomials of
smaller degree.
POLYNOMIAL GCF FACTORED
FORM

20. Step-by-Step Factoring Process
1
Identify GCF
Start by finding the greatest
common factor (GCF) of the
polynomial's terms. This will be
the first factor in the factored
form.
2 Divide by GCF
Divide each term in the
polynomial by the GCF to obtain
the remaining factor(s).
3
Arrange Factors
Arrange the GCF and the
remaining factor(s) in a way that
makes the factored form clear and
easy to understand.

21. Factor the polynomial:
:
GCF:
:

23. Try this!
𝒂 𝟓
:
A rectangular lot has an area of square meters. The length of the
rectangular lot is equal to the greatest common monomial factor of
the polynomial area. What are the dimensions of the rectangle?
12
4
(2)(2)(2)(𝑎)(𝑎)(𝑎)(𝑎)(𝑎)
(2)(2)(3)(𝑎)(𝑎)(𝑎)(𝑎)
(2)(2)(𝑎)(𝑎)(𝑎)
4

24. 𝟒 𝒂𝟑
𝟒 𝒂𝟑
𝟒 𝒂𝟑
¿𝟐𝒂𝟐
+𝟑𝒂+𝟏
4 (𝟐 𝒂𝟐
+𝟑𝒂+𝟏)

25. 𝟓 𝒙𝟐
𝒚 𝟓 𝒙𝟐
𝒚
¿𝟑 𝒙−𝟐 𝒚
𝟓 𝒙𝟐
𝒚
(𝟑 𝒙 −𝟐 𝒚 )

26. Practice Exercise:
1.

27. Practice Exercise:
2.

28. Factoring Binomials
Difference of Squares
Binomials that are the
difference of two perfect
squares can be factored as
the product of two
binomials, each containing
one of the square roots.
Sum or Difference
of Cubes
Binomials that are the sum
or difference of two perfect
cubes can be factored
using a similar method,
with the factors containing
the cube roots.
Other Binomials
For more general binomial
expressions, the factoring
process may involve
identifying common factors
or using the
sum/difference of
squares/cubes method.

29. Factoring Trinomials
Step 1
Identify the coefficients and constant
term of the trinomial.
Step 2
Find two factors of the constant term
whose sum equals the coefficient of the
linear term.
Step 3
Arrange the factors to create a factored
form of the trinomial.

30. Factoring Higher-Order Polynomials
Identify Factors
Look for common
factors among the
terms of the
polynomial,
including
coefficients and
variable factors.
Factor by Grouping
Group the terms of
the polynomial and
factor each group
separately, then
combine the
factors to find the
final factored form.
Recognize Patterns
Identify any
recognizable
patterns, such as
differences of
squares or
sums/differences
of cubes, that can
be used to factor
the polynomial.
Use Factoring
Techniques
Apply the appropriate
factoring techniques,
such as those used for
binomials and
trinomials, to break
down the polynomial
into its simplest form.

31. Factoring by Grouping
Step 1 Group the terms of the polynomial
into two or more groups, based on
common factors.
Step 2 Factor each group separately,
identifying the common factor for
each group.
Step 3 Find the common factor among the
factored groups, and use it to write
the final factored form.