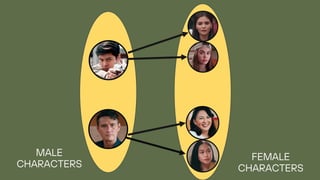
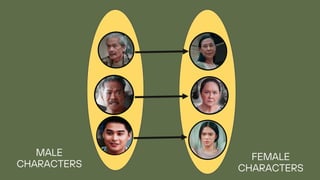
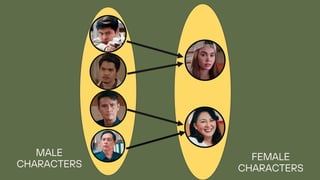
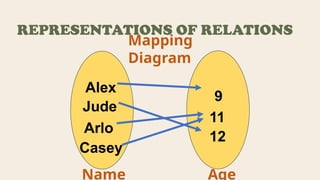
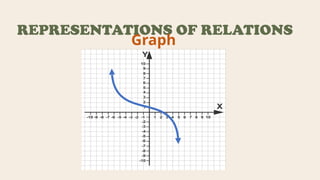
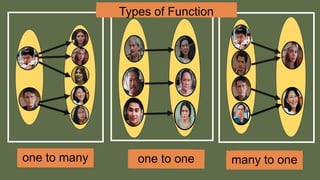
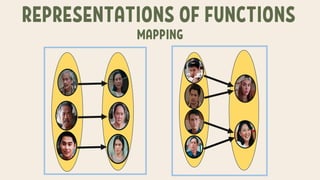
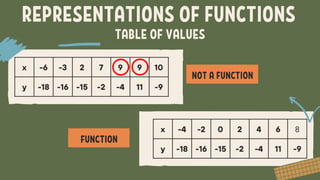
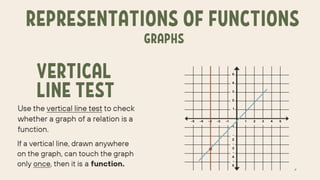
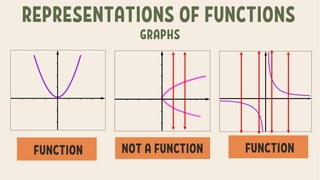
The document explains the concepts of relations and functions, including definitions, domain and range, and representation methods such as ordered pairs and graphs. It provides examples of functions and their evaluations, demonstrating how to determine the output based on given inputs. Additionally, it covers mappings and specific examples related to real-life scenarios like savings and plant growth.

6. RELATIONS AND FUNCTIONS
RELATIONS, FUNCTIONS,
VERTICAL TESTS, DOMAIN
AND RANGE

7. What are relations?
What are functions?
Presenting functions as
tables and graphs
The Vertical Line Test
LESSON OUTLINE
What is a domain?
What is a range?

8. WHAT ARE RELATIONS?
RELATIONS, FUNCTIONS,
VERTICAL TESTS, DOMAIN
AND RANGE

9. WHAT ARE RELATIONS?
{(2, -6), (1, 4), (2, 4), (0,0), (1, -6), (3, 0)}
• A relation is a set of ordered pairs that
represent a relationship.
• It is the correspondence between two
quantities

10. WHAT IS A DOMAIN?
RELATIONS, FUNCTIONS,
VERTICAL TESTS, DOMAIN
AND RANGE

11. WHAT IS A DOMAIN?
The domain of a relation is the set of all
first coordinates (x-coordinates) from
the ordered pairs.

12. GIVEN THE RELATION:
{(2, -6), (1, 4), (2, 4), (0,0), (1, -6), (3, 0)}
Domain:
D: {0, 1, 2, 3}

13. WHAT IS A RANGE?
RELATIONS, FUNCTIONS,
VERTICAL TESTS, DOMAIN
AND RANGE

14. WHAT IS A RANGE?
The range of a relation is the set of all
second coordinates (y-coordinates)
from the ordered pairs.

15. GIVEN THE RELATION:
{(2, -6), (1, 4), (2, 4), (0,0), (1, -6), (3, 0)}
Domain:
D: {0, 1, 2, 3}
Range:
R: {-6, 0, 4}

16. •Ordered pairs
•Mapping Diagram
•Table of Values
•Graphs
REPRESENTATIONS OF RELATIONS

17. Ordered pairs
REPRESENTATIONS OF RELATIONS
{(1, -6), (2, 0), (3, 1), (4,-5), (5, -6), (6, -8)}
{(5, 0), (10, 0), (15, 0)}

18. REPRESENTATIONS OF RELATIONS
5
2
1
0
11
12
19
Mapping
Diagram

19. Mapping
Diagram
REPRESENTATIONS OF RELATIONS
Alex
Jude
Arlo
Casey
9
11
12
Name Age

20. Example:
Names and their age
are a set of ordered
pairs that we could
put into a table.
REPRESENTATIONS OF RELATIONS
Table of Values

21. REPRESENTATIONS OF RELATIONS
Graph

22. WHAT IS A FUNCTION?
RELATIONS, FUNCTIONS,
VERTICAL TESTS, DOMAIN
AND RANGE

23. Input – x value
Output – y value

24. one to many one to one many to one
Types of Function

25. •Ordered pairs
•Mapping
•Table of Values
•Graphs

26. ORDERED PAIRS
y = (-1, 0), (-2, 1), (-3, 2), (-4, 3)
h = (-5, 2), (-8, -3), (-3, 2), (-8, 9)
x = (1, 2), (-3, 5), (6, 2), (-8, 5)

32. PERSON’S AGE TO THEIR NAME
STUDENT’S TO THEIR
FAVORITE SUBJECT
ELECTRICITY
BILL

33. The total savings (S) is a
function of months (m).
• Give a function S that
represents the total
savings of Mark if he
saves Php300 per month
S(m)
S(m) =
300m

34. The total number of steps
(S) is a function of the
number of hours walked
(h).
• Write a function S that
represents the number
of steps if a person takes
5000 steps per hour.
S(h)
S(m) =
5000h

35. A plant's height (H) is a
function of time in weeks
(w).
• Give a function H that
represents the height of
a plant that starts at 5
cm and grows by 2 cm
every week.
H(w
)
H(w) =
5+2w

36. EVALUATING
FUNCTIONS

39. B(t) = 2, 000, 000 + 50,000tB(t) = 2, 000, 000 + 50,000t
B(t) = 2, 000, 000 + 50,000(2
B(t) = 2, 000, 000 + 120,000
B(t) = 2, 120,
000

40. LET’S RECALL
 The total income (I) is a function of
hours (r). If Ana is paid 60 pesos per
hour, how much will she earn in 3
days, if she works 8hrs a day.

41. LET’S RECALL
 The total cost (C) of water bill is a
function of the number of cubic meter
(m). If Maynilad charges a base fee of 15
pesos plus 40 pesos per cubic meter. How
much would your water bill if you
consumed 23 cubic meters.

42. EVALUATING
FUNCTIONS

43. EVALUATING FUNCTIONS
 It is the process of determining the
value of the function at the number
assigned to a given variable.

44. EXAMPLE 1
Let f(x) = x² - 7x + 4. Find the values of
function if:
• f(-1)
• f()
• f(2x)

45. EXAMPLE 2
Let f(x) = . Find the values of function if:
• f(8)
• f(0)
• f()

46. EXAMPLE 2
Let f(x) =. Find the values of function if:
• f(5)
• f()