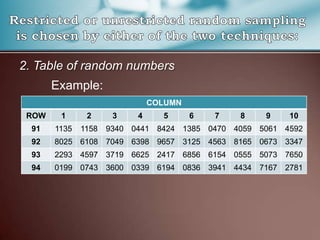
This document discusses different sampling methods that can be used in research. It defines sampling as selecting a subset of individuals from within a population to gather data and make inferences about the entire population. The key methods discussed are scientific sampling methods, like random sampling and stratified sampling, which aim to select representative samples, and non-scientific sampling methods, like purposive and quota sampling, which do not give all individuals an equal chance of being selected. Formulas are provided for determining sample size needed based on the overall population size.

1. ED 502
Methods of Research

2. Sampling

3. Population
–

4. • Saves time, money, and effort
because the number of subjects involved is small; gives a more
comprehensive information of the results of the study.
• More effective
if every individual of the population without bias has an equal chance of
being included in the sample and data are scientifically collected, analyzed, and
interpreted.
• Faster, cheaper and economical
collection, tabulation, presentation, analysis and interpretation of
data are rapid and less expensive due to small number of subjects and
few copies of the questionnaires are used.

5. • More accurate
fewer errors are made due to small size of data involved in
collection, tabulation, presentation, analysis, and interpretation.
• Gives more comprehensive information
since there is a thorough investigation of the study due to
small sample, the results give more comprehensiuve information
because all members of the population have an equal chance of being
included in the sample

6. • Sample data involve more care in preparing detailed
subclassification due to small number of subjects.
• If the sampling plan is not correctly designed and
followed, the results may be misleading
• Sampling requires an expert to conduct the study in
an area. If this is lacking, the results can be
erroneous.
• The characteristic to be observed may occur rarely
in a population, for instance, teachers over 30 years
of teaching experience or teachers with
outstanding performance.
• Complicated sampling plans are laborious to
prepare.

7. 1. State the objectives of the survey.
2. Define the population.
3. Select the sampling individual.
4. Locate and select the source list of particular
individuals to be included in the sample
5. Decide the sampling design to be used that
suits to the study either scientific or non-scientific
sampling.

8. 6. Determine the sample size by using the formula,
NV + [Se2 (1-p)]
NSe + [V2 p(1-p)]
Where:
Ss – sample size
N – population
V – standard value (2.58) of 1% level of
probability with 0.99 reliability level
Se – sampling error (0.01)
p – the largest possible proportion (0.50)

9. 7. Select the method in estimating the reliability of
the sample either test-retest, split-half, parallel-
forms, or internal consistency.
8. Test the reliability of the sample in a pilot
institution.
9. Interpret the reliability of the sample.
10. Choose experts to administer the research
instruments.

10. • Step 1. Determine the total population (N) as
assumed subjects of the study.
• Step 2. Get the value of V(2.58), Se (0.01), and
p (0.50).
• Step 3. Compute the sample size using the
formula:
NV + [Se2 (1-p)]
NSe + [V2 p(1-p)]

11. For instance, the total population (N) is
900, the standard value (V) at 1% level of
probability is 2.58 with 99% reliability and has
sampling error (Se) of 1% or 0.01 and the
proportion (p) of a target population is 50% or
0.50. Then the sample size is computed as
follows:

12. Given:
N = 900
V = 2.58
Se = 0.01
p = 0.50
NV + [Se2 (1-p)]
NSe + [V2 p(1-p)]
900(2.58) + (0.01)2 x (1– 0.50)
900(0.01)+(2.58)2 x 0.50(1- 0.50)
2322 + 0.0001 x 0.50
9 + 6.6564 x 0.50 (0.50)
2322 + 0.00005
9 + 6.6564 (0.25)
2322.00005
9 + 1.6641
2322.00005
10.6641
Ss = 218

13. The sample size for a population of 900 is
218. This sample, 218, will represent the
subjects of the study.

14. 1. Scientific Sampling
- each member of the population is given an
equal chance of being included in the sample
2. Nonscientific Sampling
- not all of the members in the population
are given an equal chance of being included in the
sample

15. SCIENTIFIC SAMPLING
1. Restricted random sampling
2. Unrestricted random sampling
3. Stratified sampling
4. Systemic sampling
5. Multistage sampling
6. Cluster sampling

16. • Used in homogeneous population
• Samples drawn from a homogeneous population
are likely to arrive at accurate values of the
population characteristics

17. • Best random sampling design due to no
restrictions imposed, and every member in the
population has an equal chance of inclusion in
the sample

18. 1. Lottery technique
- this technique is useful if the population is
small
- Individual in the population is assigned a
number which is written on a piece of paper. The
pieces of paper are rolled and placed in a box and
mixed thoroughly. The rolled papers are drawn
from the box one at a time.

19. 1. Lottery technique
Example: The population is 175. There will
be 175 pieces of paper numbered 001 to 175.
These papers will be drawn from 001 to 132 will be
chosen as samples since the sample size of 175 is
132.

20. 2. Table of random numbers
- applicable to a large number of population
- It consists of digits so selected that no
systematic relation exists between any sequence
of digits in the table, regardless of whether the
table is read vertically, horizontally, right or left, or
in any other way.

21. 2. Table of random numbers
Example:
COLUMN
ROW 1 2 3 4 5 6 7 8 9 10
91 1135 1158 9340 0441 8424 1385 0470 4059 5061 4592
92 8025 6108 7049 6398 9657 3125 4563 8165 0673 3347
93 2293 4597 3719 6625 2417 6856 6154 0555 5073 7650
94 0199 0743 3600 0339 6194 0836 3941 4434 7167 2781

22. 2. Table of random numbers
Example: If the population is 5000, each
member must be assigned an identifying number
ranging from 0001 to 5000. to get the sample size
of 250 from 5000 population, the researcher will
randomly get 250 numbers from the table. If the
number exceeds the number of population (e.g.
6154), it will be discarded.

23. • divides first the population into two or more
strata
Example: A school has 5000 students: 3500
females and 1500 males. Sample size of 3500 is
244, so a sample of 244 are drawn by random
technique from the subpopulation or stratum of
females. Sample size of 1500 is 232, so a sample
of 232 are drawn by random technique from the
subpopulation or stratum of males.

24. • individuals in the population are arranged in a
methodical manner, for instance, alphabetical or
chronological (age, experience or academic
rank), and the nth name may be selected in the
construction of the sample.

25. Example: there are 2500 population in the
study. To choose a sample, the 2500 are arranged
alphabetically or chronologically. They are
numbered 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 for the first
set. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 for the second set
and so on until the desired population, 2500, are
numbered by 10s. Every 10th of the set is selected
as part of the sample until it reaches the sample
size of 2500 which is 242.

26. • done in several stages
• Individuals are grouped into a hierarchy of
units, and sampling is done consecutively.
Example: In a nationwide study, regions are
chosen as first stage; provinces as second stage;
municipalities, third stage; barangay, fourth stage.

27. • population is grouped into clusters or small
units.
Example: blocks or districts, in a municipality
or city composed of population individuals and are
selected either by random sampling or systemic
sampling.

28. NONSCIENTIFIC SAMPLING
1. Purposive sampling
2. Incidental sampling
3. Quota sampling

29. • based on selecting the individuals as samples
according to the purpose of the researcher as
his controls. An individual is selected as part of
the sample due to good evidence that he is a
representative of the total population.

30. • applied to those samples which are taken
because they are the most available.
• The investigator simply takes the nearest
individuals as subjects of study until the sample
reaches the desired size.

31. • done by merely looking for individuals with the
requisite characteristics.
• Usually prepared by the main office with
instructions to the field researchers to gather
data from samples that meet the prescribed
criteria or characteristics