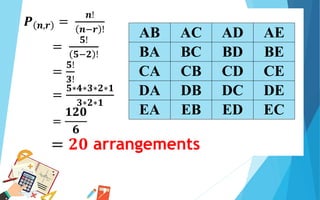
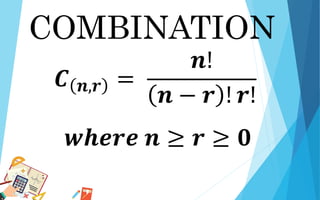This document discusses combinations and provides examples of calculating combinations. It defines a combination as a subset of objects chosen from a larger set in any order. It provides the formula for combinations, which is the number of ways of choosing r objects from n objects, represented as C(n,r) = n!/(n-r)!r!. Several examples are given of using this formula to calculate the number of combinations in different scenarios.

2. Given 5 letters
Arrange these letters taken 2 at a time.
How many ordered arrangements will
be there?
REVIEW
A B C D E

3. 𝑷 𝒏,𝒓 =
𝒏!
𝒏−𝒓 !
=
𝟓!
𝟓−𝟐 !
=
𝟓!
𝟑!
=
𝟓∗𝟒∗𝟑∗𝟐∗𝟏
𝟑∗𝟐∗𝟏
=
𝟏𝟐𝟎
𝟔
= 𝟐𝟎 arrangements
AB AC AD AE
BA BC BD BE
CA CB CD CE
DA DB DC DE
EA EB ED EC

5. COMBINATION

6. - is a subset of a lager
set of objects refer to
the number of ways we
can CHOOSE items in
ANY ORDER.
COMBINATION

7. 𝑪 𝒏,𝒓 =
𝒏!
𝒏 − 𝒓 ! 𝒓!
𝒘𝒉𝒆𝒓𝒆 𝒏 ≥ 𝒓 ≥ 𝟎
COMBINATION

8. Given 5 letters
Taken 2 at a time.
Example 1:
A B C D E

9. AB
BA
Combination of

11. Example 2:

12. 8 students are qualified for a
certain scholarship. However,
only 5 students will be
granted. How many different
ways of 5 students can be
selected?
Example 3:

13. A famous fast-food restaurant
device a new strategy to attract
more customers and this new
strategy of them is called Mix and
Match Combos. Given 4 options for
the main dish and 5 options for the
side dish, how many possible
combos consisting of 1 main dish
and 2 side dish can a costumer
choose?
Example 4:

14. TASK 1:
As a party coordinator, you
prepared 1o games for the
children party. If there is just
enough time to play 4 games, in
how many ways can you choose
the 4 games to play?
APPLICATION TASKS:

15. TASK 2:
During a radio show, the DJ
can play 10 songs. In how
many way can he select the
songs to play if he has 15
songs to choose from?
APPLICATION TASKS:

16. TASK 3:
In how many ways can a
committee of 5 teachers be
formed from a department
of 12 teachers?
APPLICATION TASKS:

17. TASK 4:
Sebastian’s Ice cream shop offers 15
flavors of ice cream and 10
toppings. How many combinations
can be made from choosing 3
flavors of ice cream and 5 toppings?
APPLICATION TASKS:

18. Question 1:
What is combination?
5 PTS
Generalization:

19. Question 1:
What is combination?
5 PTS
Generalization:
Combination is a subset of a lager set of
objects refer to the number of ways we can
choose items in any order.

20. Question 2:
The formula of Combination
of n objects taken r at a time.
5 PTS
Generalization:

21. Question 2:
The formula of Combination
of n objects taken r at a time.
5 PTS
Generalization:
𝑪 𝒏,𝒓 =
𝒏!
𝒏 − 𝒓 ! 𝒓!

22. Question 3:
Permutation is about
_______ and Combination is
about_________. 5 PTS
Generalization:

23. Question 3:
Permutation is about
_______ and Combination is
about_________. 5 PTS
Generalization:
Permutation is about arranging objects and
Combination is about choosing objects.

24. Evaluation:
1.Evaluate: 𝑪 𝟏𝟐, 𝟑
2.Evaluate: 𝑪 𝟕, 𝟐 ∗ 𝑪(𝟑, 𝟐)
3.From a group of 12 scholars, in how many ways can a
university send 4 of them to the conference?
4.How many combinations can be made from the word
CHOICE if the letters are taken 3 at a time?
5.In how many ways can a committee of 7 students be
chosen from 6 juniors and 8 seniors if there must be at
least 4 seniors in the committee?

25. Assignment
Order
Matters
Order Doesn’t
Matter
Permutation Combination n r Answer
Choose 5 people from ten on
the waiting list to board the
plane
Choose the first 5 people from
ten on the waiting list to board
the plane
Choose 7 songs out of 12 to
make a specific playlist for the
party
Choose 7 songs out of 12 to
download.
Choose 3 students to represent
the class in a quiz bee.
Choose 3 students from 30 to
be the president, the vice
president and secretary.
Identify a) if order matters or not in each situation, b) it it’s permutation or a
combination problem, c) the values of n and r, and then d) compute the answer.