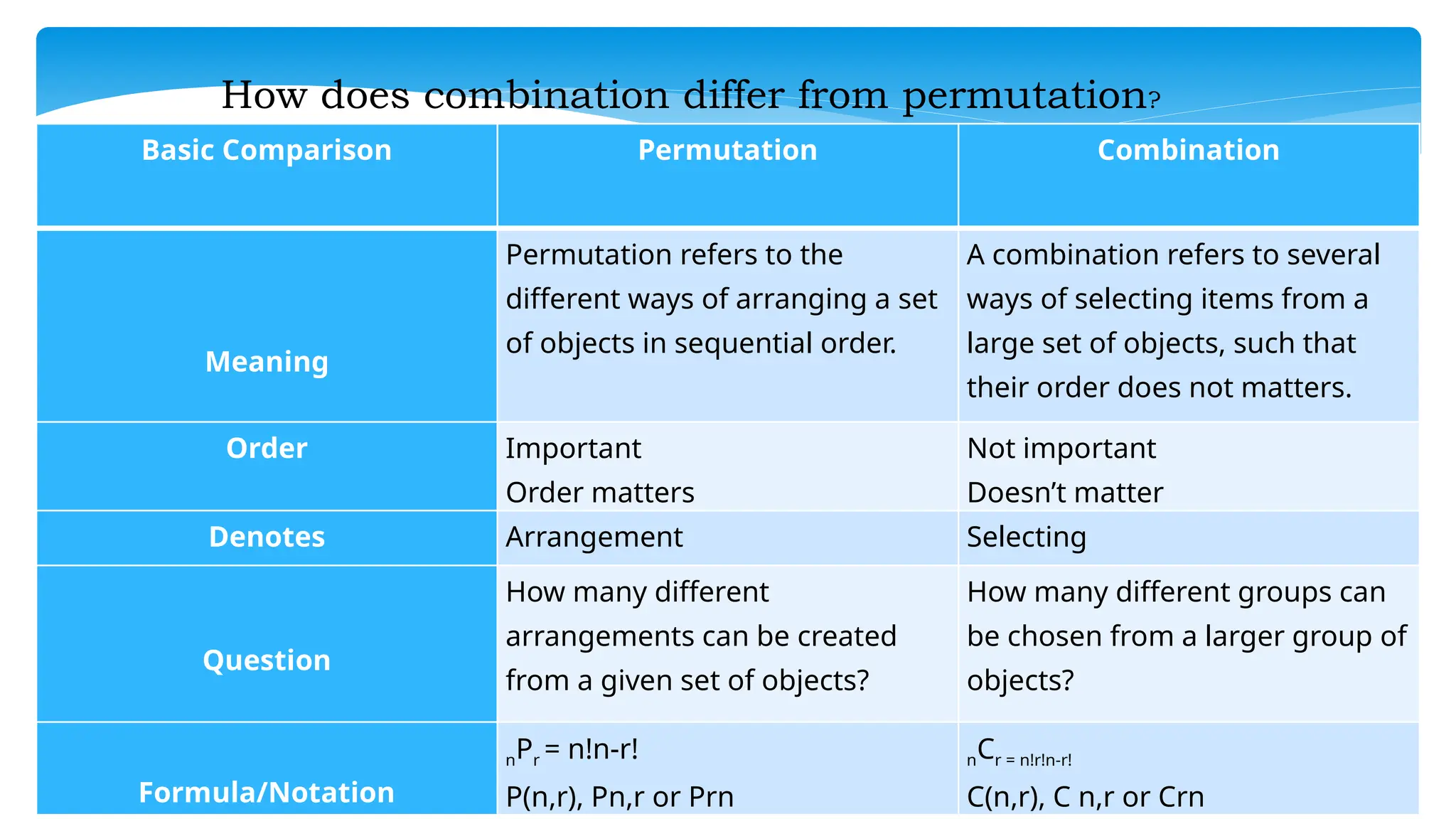
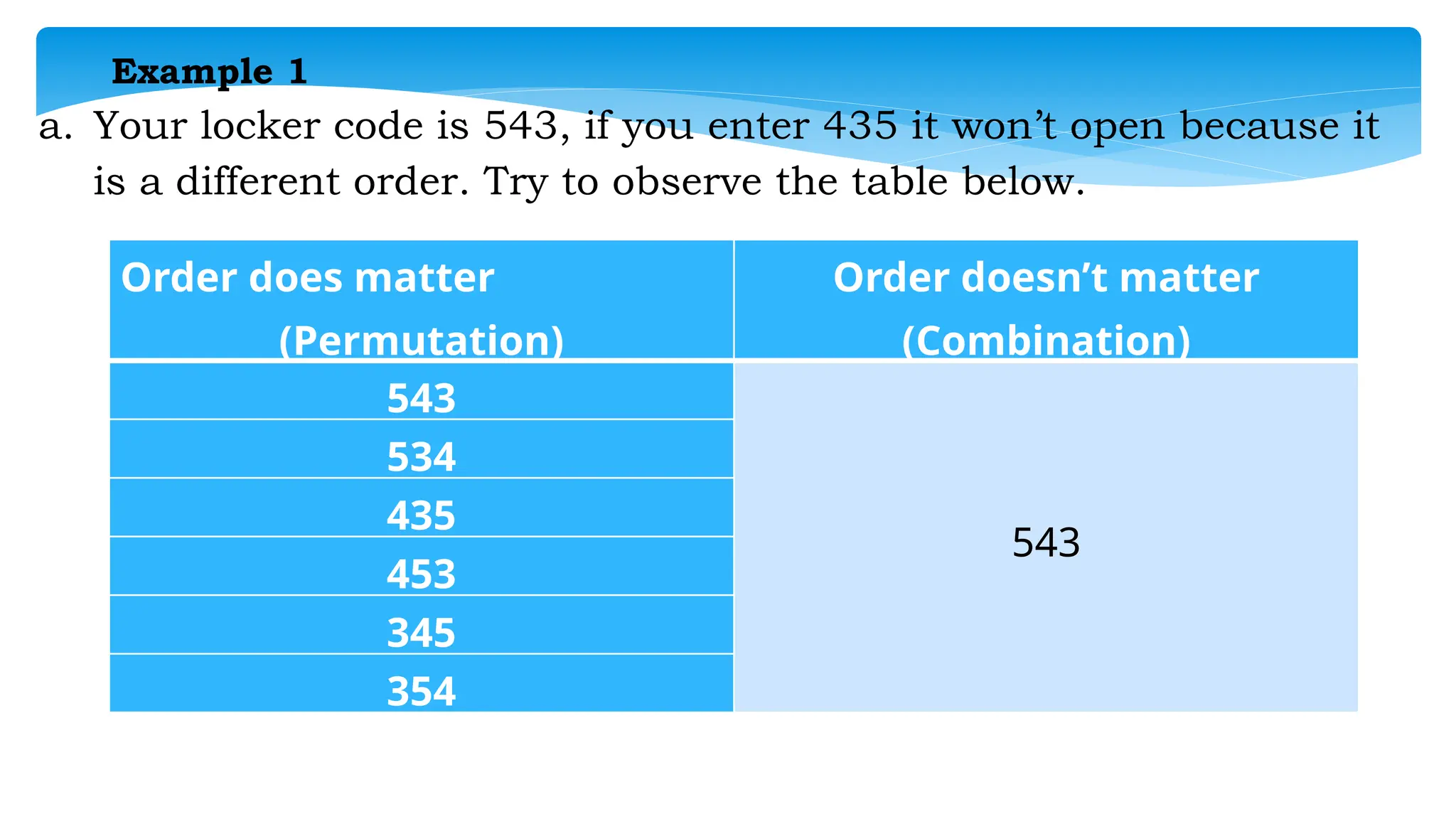
The document outlines a group activity where students participate in a game selecting representatives to answer questions based on culinary and mathematical concepts, particularly focusing on permutations and combinations. It explains the difference between permutations (order matters) and combinations (order does not matter), providing examples and formulas for both concepts. Additionally, it includes assessment rubrics, application problems, and evaluation questions centered on the understanding of combinations and permutations.

2. The students will be divided into two groups. Each group
should select a representative to answer for the group.
Groupmates are allowed to coach the representative. If the
representative could not answer and admit to surrender,
then the other members have the right to answer the
problem. The group who got the highest score will be the
winner of the game. You will be given 1 minute to answer
per problem.
COMBINE ME!

3. 1. Apple, banana, papaya, pineapple, melon,
avocado, nestle cream, condensed milk.
FRUIT SALAD
2. Bitter gourd, eggplant, squash, yard-long beans,
bagoong.
PINAKBET
3. Tapa, fried rice, fried egg.
TAPSILOG
Let’s start the game!

4. 4. Hotdog, ground pork, tomato sauce, cheese,
condensed milk &pasta.
SPAGHETTI
5. Nestle cream, macaroni, condensed milk,
pineapple, fruit cocktail.
MACARONI SALAD

5. Directions: Identify if the given situation is a permutation or NOT.
_____ 1. A company has 12 members in its board of directors who will elect a
president, vice president, secretary, and treasurer among themselves. In how
many ways can this be done?
______2. In how many ways can identical pencils be shared by pupils?
_____3. In how many ways can bookmarks be divided among bookworms?
_____4. In how many different ways may 8 numbers be arranged in a
spinner?
_____ 5. There are 8 boys in a basketball team. In how many ways can the
coach select 5?

6. “Shake it to the right, shake it to the left”
 In a Regional Encampment held at Cogon, Dipolog
City, there are six troop leaders. How many
handshakes are there if each troop leader shakes
hands with all the others once?

7. Guide Questions:
1. What kind of situation is being presented?
2. How are you going to answer this problem?
3. What formula are you going to use?

8. COMBINATION OF AN OBJECT

9.  Define and illustrate combination of
objects.
 Differentiate permutation from
combination of n objects taken r at a time.
 Relate combination in real life situation.
OBJECTIVES

11. Combination refers to the selection of objects where order is not
important. That is, changing the order of the objects does not create
a new combination.
For instance, the 3 combinations of the 3 letters T, I, and N taken
2 at a time are: TI, TN, and IN
TI and IT are considered one combination. Similarly, IN and NI
and TN and NT are the same combinations.
There is only one combination that can be made from the letters T,
I, and N taken 3 at a time. That is TIN
TIN, TNI, INT, NIT, ITN, and NTI are considered one
combination.
The combination of n things or objects taken r at a time can be
denoted by : C(n,r).

12. Basic Comparison Permutation Combination
Meaning
Permutation refers to the
different ways of arranging a set
of objects in sequential order.
A combination refers to several
ways of selecting items from a
large set of objects, such that
their order does not matters.
Order Important
Order matters
Not important
Doesn’t matter
Denotes Arrangement Selecting
Question
How many different
arrangements can be created
from a given set of objects?
How many different groups can
be chosen from a larger group of
objects?
Formula/Notation
nPr = n!n-r!
P(n,r), Pn,r or Prn
nCr = n!r!n-r!
C(n,r), C n,r or Crn
How does combination differ from permutation?

13. Example 1
a. Your locker code is 543, if you enter 435 it won’t open because it
is a different order. Try to observe the table below.
Order does matter
(Permutation)
Order doesn’t matter
(Combination)
543
543
534
435
453
345
354

14. •Consider the number of permutations of the 4 marbles with colors
Red, Green, Blue and Yellow taken 3 at a time.
The 24 permutations are listed below:
6 permutations
6 permutations
6 permutations
6 permutations
There are 24 permutations but only 4 combinations. This is
illustrated below:
1 Combination
1 Combination
1 Combination
1 Combination

16. Rubric in Assessing Students’ Performance (Group
Task)
STANDARD
S
4 3 2 1
Understandi
ng of the
Task
Demonstrate
d substantial
understandi
ng of the
content,
processes,
and
demands
Demonstrate
d
understandin
g of the
content and
task, even
though some
supporting
ideas or
details may
have been
overlooked
Demonstrate
d gaps in
their
understandi
ng of the
content and
task
Demonstrated
little
understanding
of the content

17. SCAVENGER HUNT
A. 15
It refers to
the
selection of
objects
where
order is not
important.
B. C(n,r)=
In how many
ways can 4
mango trees
be planted in
6 holes dug
by the
teachers of
DCNHS(Barra
)?
C. 8
How will
you write C
(10, 4) in
expanded
form?
D.
Combination
In how
many ways
can a
doctor
choose 4
from 10
interns to
assist her
in n
E. 210
Solve:C (8,
7).

18. APPLICATION:
Solve the following problems:
1. C(8,3)
2. Alice has 6 chocolates. All of the chocolates are
of different flavors. She wants to give two of her
chocolates to her friend. How many different
combinations of chocolates can Alice make from
six chocolates.

19. GENERALIZATION:
Who can give an example
where combination is applied
in real life situation?
Answer:
1. Cooking
2. Swertres Lotto – Rumble,
6/45

20. EVALUATION:
Multiple Choice: Directions: Read the questions carefully. Encircle the letter
of the correct answer.
1. What is the expanded form of 10C2?
A. C(10, 2) =10!10-2! C. C(10, 2) = 10!10-2!2!
B. C(10, 2) =2!2-10!10! D. C(10, 2) = 2!2-10!
2. It refers to several ways of selecting items from a large set of objects,
such
that their order does not matter?
A. combination C. integration
B. differentiation D. permutation
Same questions for Face – to – Face, Online
& Modular (Pages 8 – 9)

21. 3. Which of the following experiments will determine that order is NOT important?
A. Selecting the top 3 winners in Math Quiz Bowl.
B. Setting a 4-digit code in a vault.
C. Buying 3 out 7 designs of face mask.
D. Assembling a jigsaw puzzle.
4. How many ways can 5 cars be parked if there are 7 available parking
spaces?
A. 1260 B. 1540 C. 2230 D. 2520
5. How many ways can Charice invites 3 or more friends to her birthday party
if she has on 5 friends?
A.5 B. 10 C. 16 D. 50

22. VALUES INTEGRATION:
There are numerous ways to
WONDER. Take your time.
EXPLORE for without WONDER,
life is merely an existence . . .

23. Assignment:
1. Study more on problem solving
about combination.