The document provides a detailed explanation of permutations and combinations, highlighting their definitions, formulas, and differences. It includes solved examples and practice questions to illustrate how to apply these concepts in various mathematical contexts. Additionally, it addresses frequently asked questions related to permutations, combinations, and their real-life applications.

1. PERMUTATION & COMBINATION
Abhishek Sonker

2. Permutation and combination are ways to choose objects from a group, with or
without replacement.
● Permutation arranges objects with specific order.
● Combination selects objects without considering order.
● Both are important in Mathematics.

3. Table of Contents
● Permutation Definition
● Combination Definition
● Formulas
● Difference Between Permutation and Combination
● Uses
● Video Lessons
● Solved Examples
● Practice Questions
● FAQs

4. What is Permutation?
In math, permutation means arranging set members in order.
● It involves re-arranging ordered sets.
● Permutations appear in various math areas.

5. What is a Combination?
Combination is selecting without order.
● Order doesn't matter in combinations.
● For n things taken k at a time.
● Repetition or without repetition.

6. Formulas
There are many formulas involved in permutation and combination concepts. The two
key formulas are:
Permutation Formula
The choice of r things from a set of n things without replacement and where the order
matters.
nPr = (n!) / (n - r)!

7. Combination Formula
The choice of r things from a set of n things without replacement and where order
doesn't matter.

8. Difference Between Permutation and Combination
Permutation Combination
Arranging people, digits, numbers,
alphabets, letters, and colours
Selection of menu, food, clothes, subjects,
team.
Picking a team captain, pitcher and
shortstop from a group.
Picking three team members from a group.
Picking two favourite colours, in order, from
a colour brochure.
Picking two colours from a colour brochure.
Picking first, second and third place
winners.
Picking three winners.

9. Uses
Permutation is used for the list of data (where the order of the data matters).
Combination is used for a group of data (where the order of data doesn’t matter).

10. Solved Examples of Permutation and Combinations
Example 1:
Find the number of permutations and
combinations if n = 12 and r = 2.
Solution:
Given,
n = 12
r = 2
Using the formula given above:
Permutation:
nPr = (n!) / (n-r)! =(12!) / (12-2)! = 12! / 10! = (12 x 11
x 10! )/ 10! = 132
Combination:
nCr = n!
r!(n-r)!
12!
2!(12-2)!
12!
2!(10)!
12 x 11 x 10!
2!(10)!
= = = 66

11. Solved Examples of Permutation and Combinations
Example 2:
In a dictionary, if all permutations of the letters of the word AGAIN are arranged in an order. What is the 49th
word?
Solution:
This accounts up to the 48th word. The 49th word is “NAAGI”.
Start with the letter A The arranging the other 4 letters: G, A, I, N = 4! = 24 First 24 words
Start with the letter G arrange A, A, I and N in different ways: 4!/2! = 12 Next 12 words
Start with the letter I arrange A, A, G and N in different ways: 4!/2! = 12 Next 12 words

12. Solved Examples of Permutation and Combinations
Example 2:
In how many ways a committee consisting of 5 men and 3 women, can be chosen from 9 men and 12 women?
Solution:
Choose 5 men out of 9 men = 9C5 ways = 126 ways
Choose 3 women out of 12 women = 12C3 ways = 220 ways
Total number of ways = (126 x 220)= 27720 ways
The committee can be chosen in 27720 ways.

13. Permutation and Combination – Practice Questions
Question 1: In how many ways can the letters be arranged so that all the vowels come
together? Word is “IMPOSSIBLE.”
Question 2: In how many ways of 4 girls and 7 boys, can be chosen out of 10 girls and
12 boys to make the team?
Question 3: How many words can be formed by 3 vowels and 6 consonants taken from
5 vowels and 10 consonants?

14. Frequently Asked Questions
Q1 What do you mean by permutations and combinations?
● Permutation arranges objects or numbers in a specific order.
● Combinations select objects or numbers without caring about their order.
Q2 Give examples of permutations and combinations.
● Permutations: Example with "GREAT" - 5P2 = 5! / (5-2)!
● Combinations: Example with vowels of "GREAT" - 5C2 = 5! / [2!(5-2)!]

15. Frequently Asked Questions
Q3 What is the formula for permutations and combinations?
● Permutation: nPr = n!/(n-r)!
● Combinations: nCr = n!/[r! (n-r)!]
Q4 What are the real-life examples of permutations and combinations?
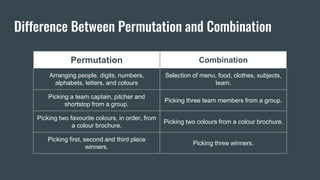
● Permutations: Arrange people, digits, numbers, alphabets, letters, colors.
● Combinations: Select menu, food, clothes, subjects, team.
Q5 Write the relation between permutations and combinations.
The formula for permutations and combinations is related: nCr = nPr / r!

16. Frequently Asked Questions
Q6 Give the applications of permutation and combination in mathematics.
In math, permutations and combinations are used in probability, relations, functions,
set theory, and more.
Q7 What is the factorial formula?
The factorial formula calculates permutations and combinations. It's the product of
numbers from 1 to n, like 3! = 3 × 2 × 1 = 6.
Q8 What does nCr represent?
nCr is the count of combinations choosing 'r' items from 'n' objects.