The document discusses jittered sampling and its implications for minimizing star discrepancy in quasi-Monte Carlo methods, exploring various conjectures related to point distributions. It presents theorems and results regarding the bounds of star discrepancy, the effectiveness of randomized point distributions, and the impact of dimension on the performance of these methods. Additionally, the document touches on the small ball conjecture and provides insights into recent advances and challenges in the field.

1. Jittered Sampling: Bounds and Problems
Stefan Steinerberger
joint with Florian Pausinger (Belfast), Manas Rachh (Yale)

2. Florian Pausinger (Belfast) and Manas Rachh (Yale)

3. QMC: the standard Dogma
Star discrepancy.
D⇤
N(X) = sup
R⇢[0,1]d
# {i : xi 2 R}
N
|R|
This is a good quantity to minimize because
Theorem (Koksma-Hlawka)
Z
[0,1]d
f (x)dx
1
N
NX
n=1
f (xn) . (D⇤
N) (var(f )) .
In particular: error only depends on the oscillation of f .

4. QMC: the standard Dogma
Star discrepancy.
D⇤
N(X) = sup
R⇢[0,1]d
# {i : xi 2 R}
N
|R|
Two competing conjectures (emotionally charged subject)
D⇤
N &
(log N)d 1
N
or D⇤
N &
(log N)d/2
N
.
There are many clever constructions of point set that achieve
D⇤
N .
(log N)d 1
N
.

6. QMC: the standard Dogma
D⇤
N &
(log N)d 1
N
or D⇤
N &
(log N)d/2
N
.
How would one actually try to prove this? Open for 80+ years,
that sounds bad.
Small ball conjecture seems spiritually related.

7. Interlude: the small ball conjecture
+1 1
1 +1
+1 1
1 +1
Haar functions hR on rectangles R.

8. Interlude: the small ball conjecture
All dyadic rectangles of area 2 2.

9. Interlude: the small ball conjecture
Small ball conjecture, Talagrand (1994)
For all choices of sign "R 2 { 1, 1}
X
|R|=2 n
"RhR
L1
& nd/2
.
1. Talagrand cared about behavior of the Brownian sheet.
2. The lower bound & n(d 1)/2 is easy.
3. The case d = 2 is the only one that has been settled: three
proofs due to M. Talagrand, V. Temlyakov (via Riesz
products) and a beautiful one by Bilyk & Feldheim.
4. Only partial results in d 3 (Bilyk, Lacey, etc.)

10. Interlude: the small ball conjecture
Small ball conjecture, Talagrand (1994)
For all choices of sign "R 2 { 1, 1}
X
|R|=2 n
"RhR
L1
& nd/2
.
A recent surprise
Theorem (Noah Kravitz, arXiv:1712.01206)
For any choice of signs "R and any integer 0  k  n + 1,
8
<
:
x 2 [0, 1)2
:
X
|R|=2 n
"RhR = n + 1 2k
9
=
;
=
1
2n+1
✓
n + 1
k
◆
.

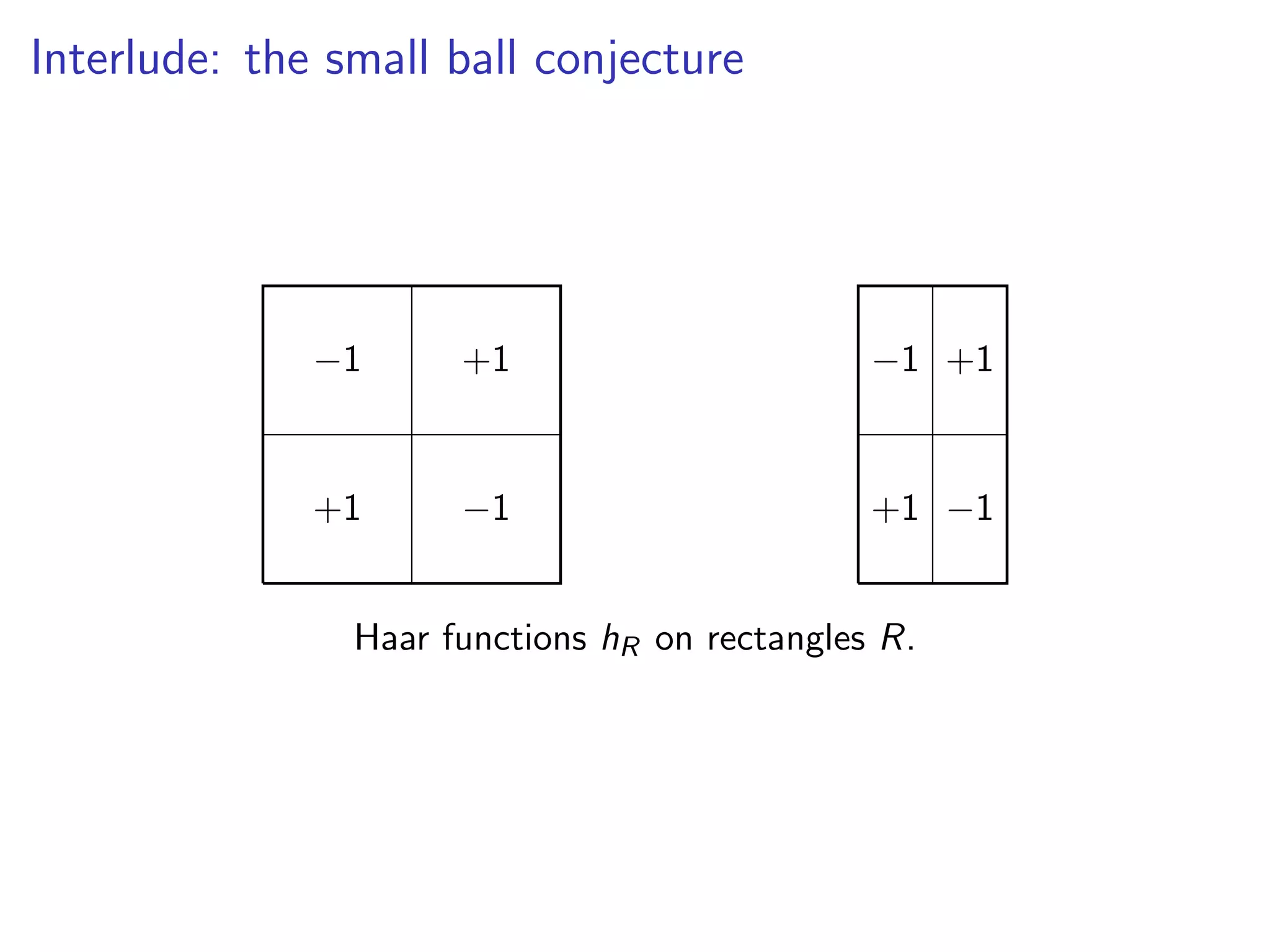
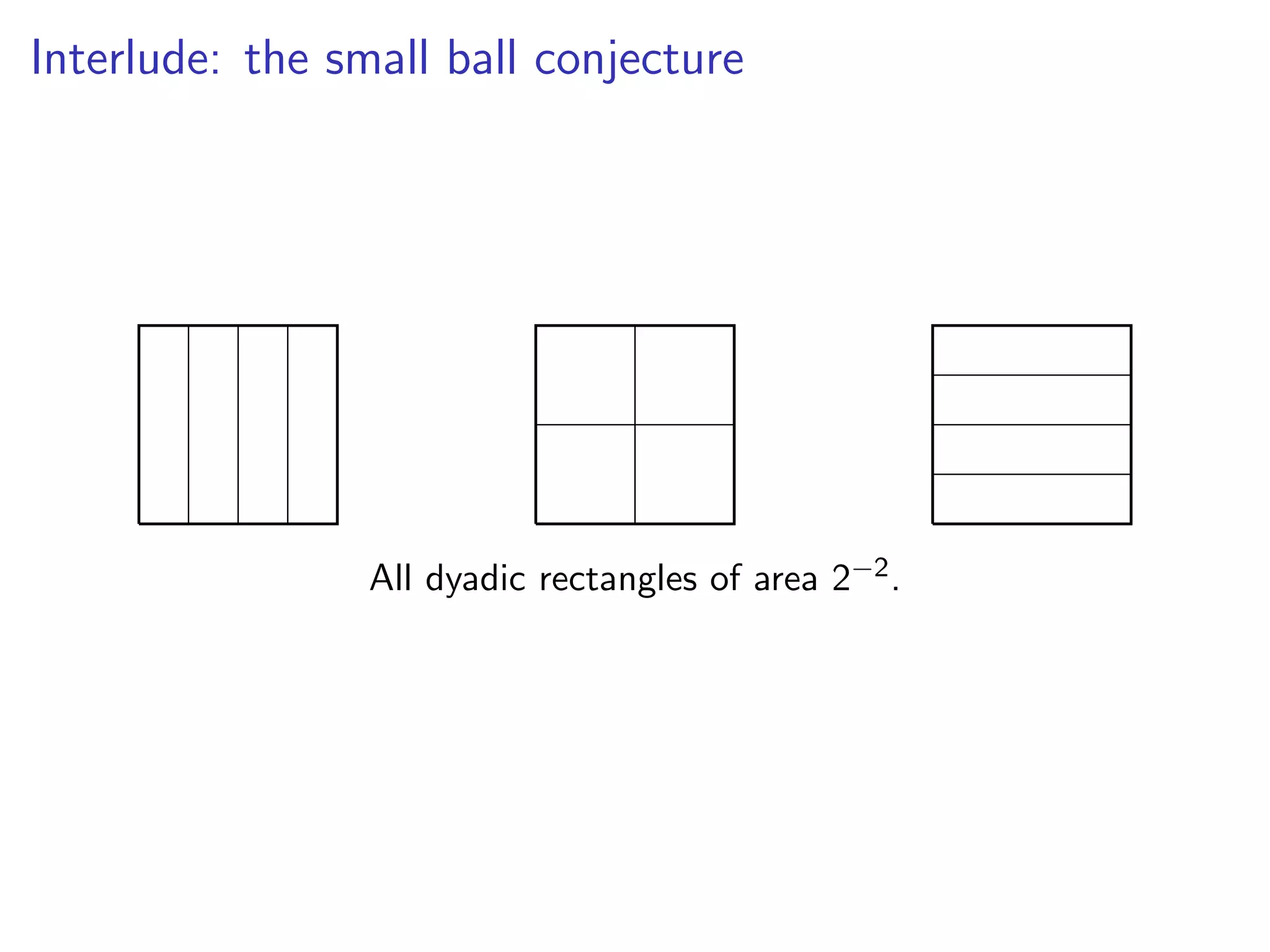
11. Problem with the Standard Dogma
Star discrepancy.
D⇤
N(X) = sup
R⇢[0,1]d
# {i : xi 2 R}
N
|R|
The constructions achieving
D⇤
N .
(log N)d 1
N
start being e↵ective around N dd (actually a bit larger even).
More or less totally useless in high dimensions.

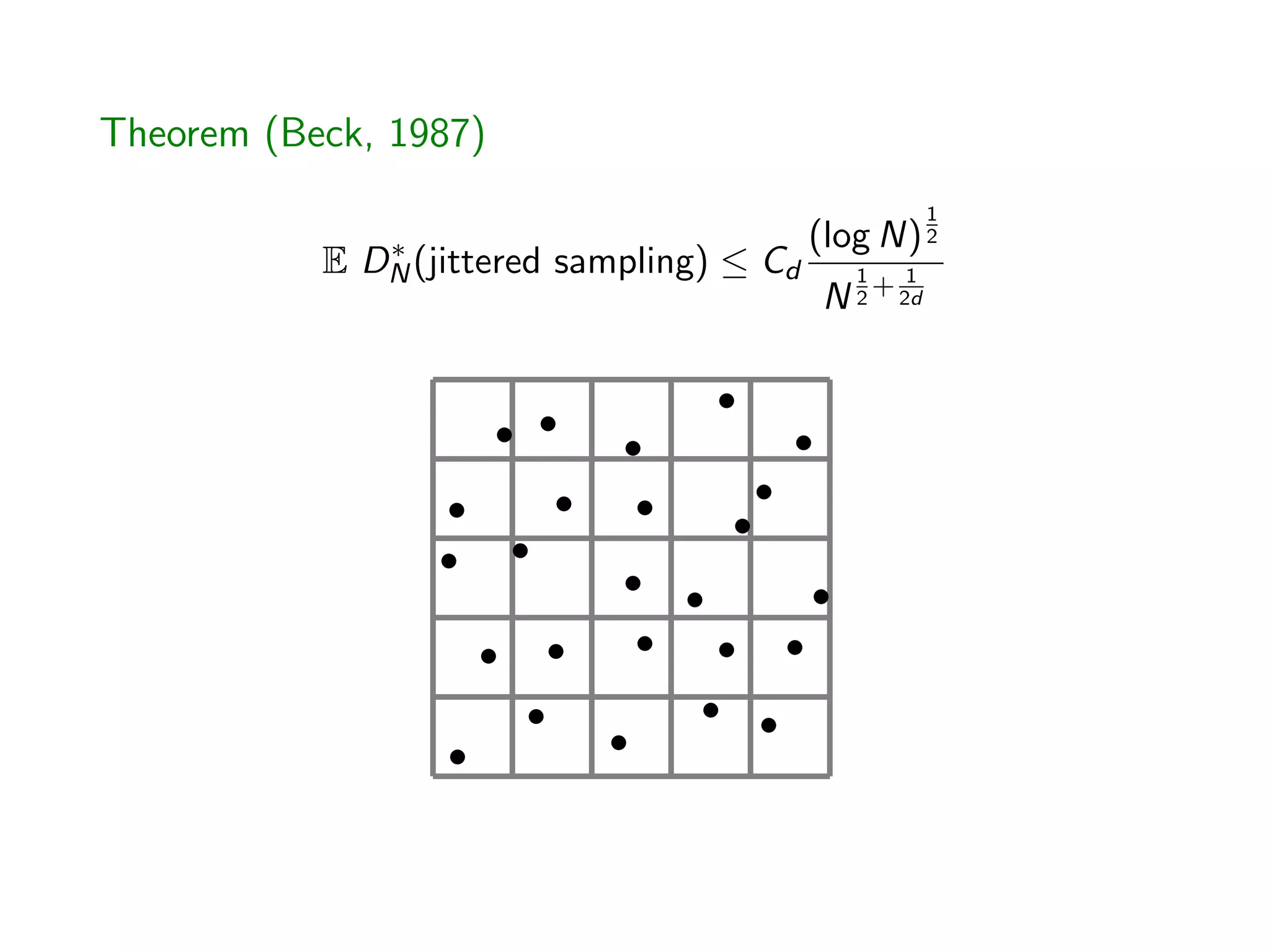
12. Monte Carlo strikes back
Star discrepancy.
D⇤
N(X) = sup
R⇢[0,1]d
# {i : xi 2 R}
N
|R|
We want error bounds in N, d!
(Heinrich, Novak, Wasilkowski, Wozniakowski, 2002)
There are points
D⇤
N(X) .
d
p
N
.
This is still the best result. (Aistleitner 2011: constant c = 10).
How do you get these points? Monte Carlo

13. Jittered Sampling
If we already agree to distribute points randomly, we might just as
well distribute them randomly in a clever way.
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•

14. Bellhouse, 1981

15. Cook, Porter & Carpenter, 1984

16. Cook, Porter & Carpenter, 1984

17. A Recent Application in Compressed Sensing (Nov 2015)

18. Theorem (Beck, 1987)
E D⇤
N(jittered sampling)  Cd
(log N)
1
2
N
1
2
+ 1
2d
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•

19. Theorem (Beck, 1987)
E D⇤
N(jittered sampling)  Cd
(log N)
1
2
N
1
2
+ 1
2d
I a very general result for many di↵erent discrepancies
I L2 based discrepancies (Chen & Travaligni, 2009)
I Problem: same old constant Cd (might be huge, the way the
proof proceeds it will be MASSIVE)

20. Theorem (Pausinger and S., 2015)
For N su ciently large (depending on d)
1
10
d
N
1
2
+ 1
2d
 ED⇤
N(P) 
p
d(log N)
1
2
N
1
2
+ 1
2d
.
I ’su ciently large’ is bad (talk about this later)
I lower bound can probably be improved
I upper bound not by much

21. How the proof works
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•

22. How the proof works
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•

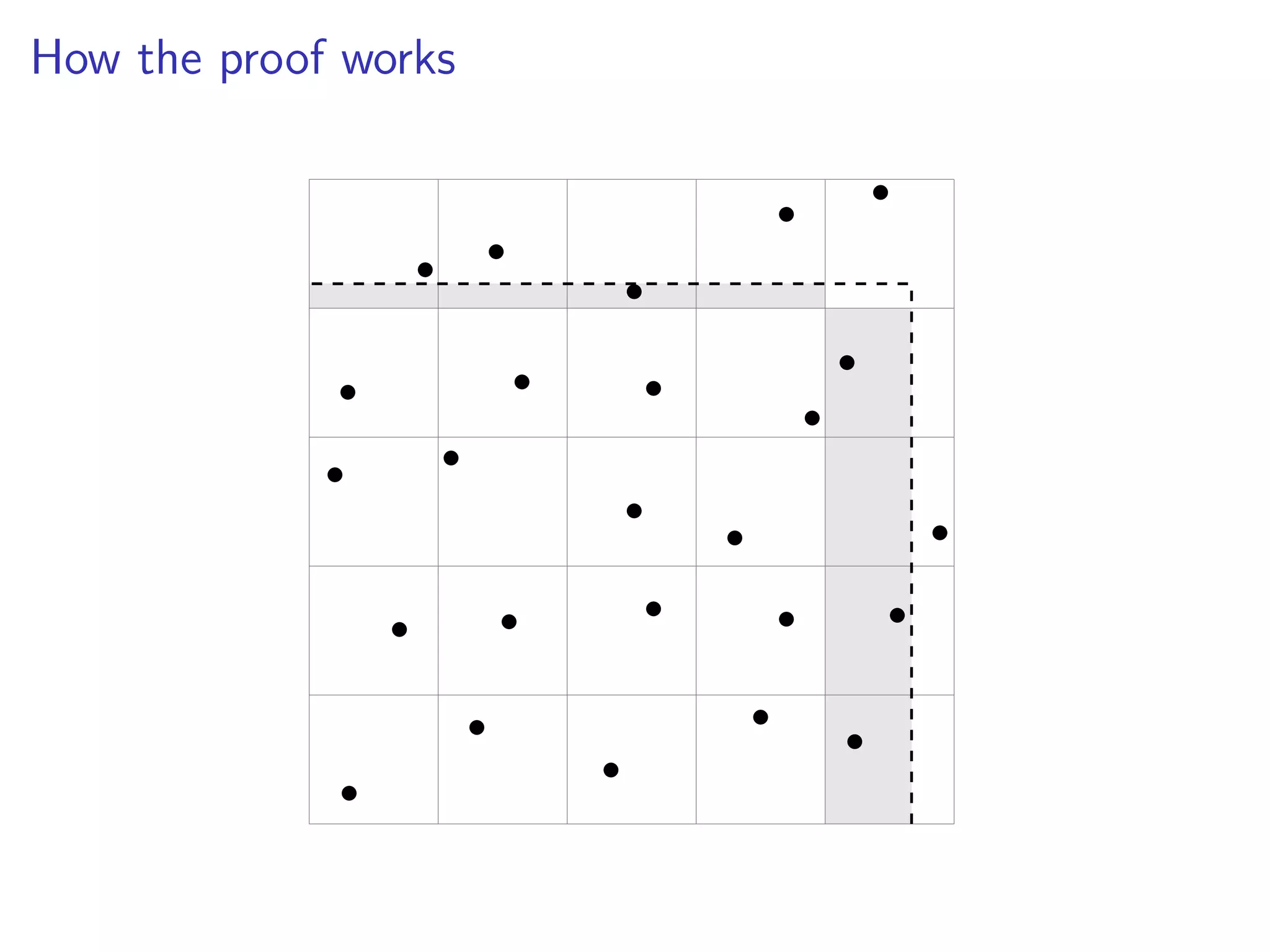
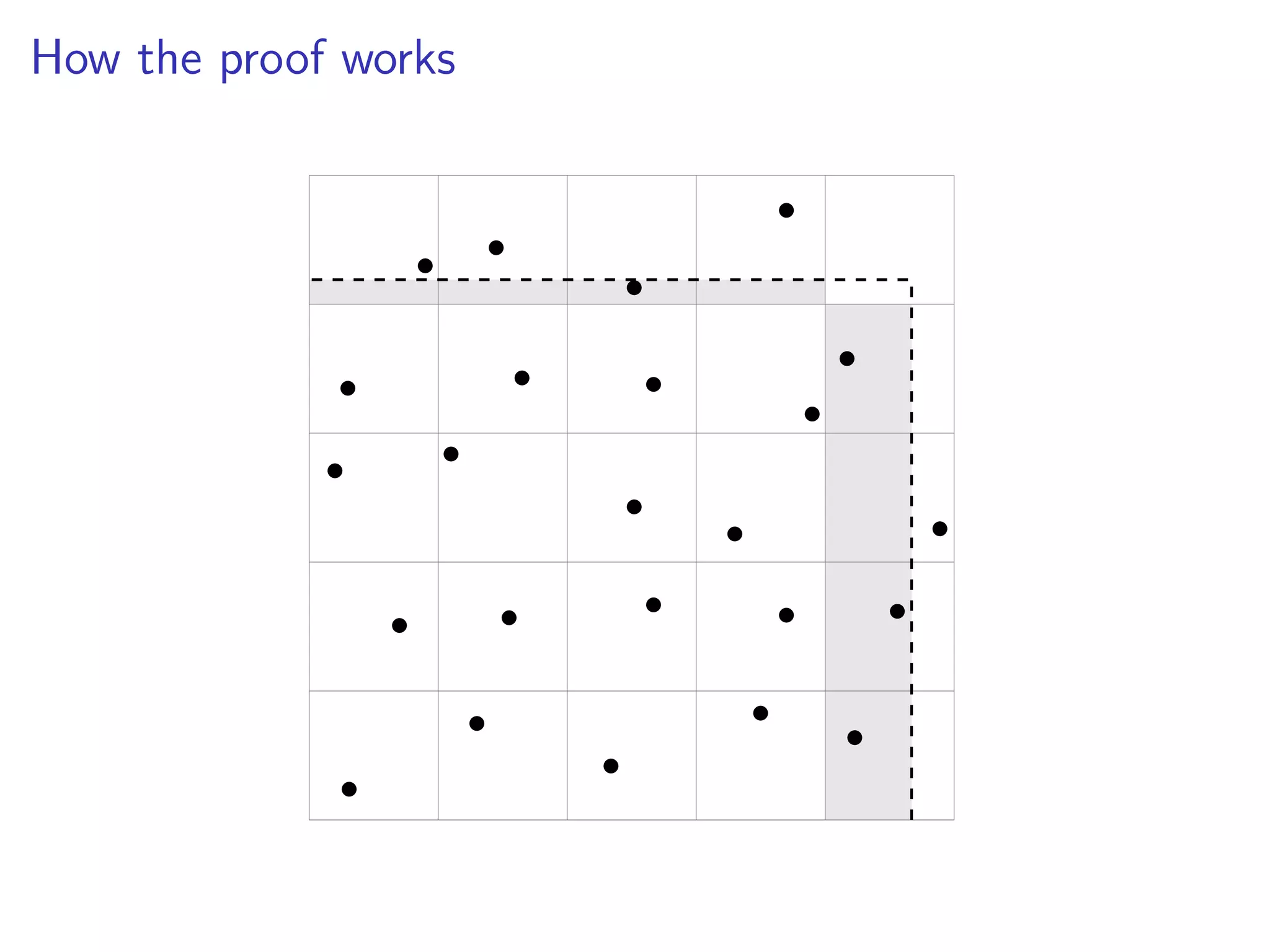
23. How the proof works
• •
•
•
Maximize discrepancy over
p
N dimensional set in [0, N 1/2].
DN ⇠
pp
N
p
N
1
p
N
=
1
N3/4
.
I lose a logarithm
I union bound on the other cubes

24. Large
Large
Large
smallsmall
small
The large contribution
comes from codimension 1 sets.

25. In d dimensions, we therefore expect the main contribution of the
discrepancy to behave like
DN ⇠
p
N
d 1
d
N
d 1
d
1
N
1
d
=
1
N
d 1
2d
1
N
1
d
=
1
N
d+1
2d
.
Of course, there is also a log. Adding up this quantity d times
(because there are d fat slices of codimension 1) gives us an upper
bound of
DN .
d
p
log N
N
d+1
2d
.
Want to improve this a bit: standard Bernstein inequalities aren’t
enough.

26. Sharp Dvoretzy-Kiefer-Wolfowitz inequality (Massart, 1990)
If z1, z2, . . . , zk are independently and uniformly distributed
random variables in [0, 1], then
P
✓
sup
0z1
# {1  `  k : 0  z`  z}
k
z > "
◆
 2e 2k"2
.
limit ! Brownian Bridge ! Kolmogorov-Smirnov distribution

27. Refining estimates
This yields a refined Bernstein inequality for very quickly decaying
expectations.

28. Rumors!
Figure: Benjamin Doerr (Ecole Polytechnique (Paris))
Benjamin Doerr probably removed a
p
log d (?). Sadly, still not
e↵ective for small N (?).

29. What partition gives the best jittered sampling?
You want to decompose [0, 1]2 into 4 sets such that the associated
jittered sampling construction is as e↵ective as possible. How?
•
•
•
•
Is this good? Is this bad? Will it be into 4 parts of same volume?
We don’t actually know.

30. Jittered sampling always improves: variance reduction
Decompose [0, 1]d into sets of equal measure
[0, 1]d
=
N[
i=1
⌦i such that 8 1  i  N : |⌦i | =
1
N
and measure using the L2 discrepancy
L2(A) :=
Z
[0,1]d
#A [0, x]
#A
|[0, x]|
2
dx
!1
2
.
Observation (Pausinger and S., 2015)
E L2(Jittered Sampling⌦)2
 E L2(Purely randomN)2
,

31. Main Idea: Variance Reduction
(What happens in L3?)

32. How to select 2 points: expected squared L2
discrepancy
MC
0.0694 0.0638 0.0555 0.05
•
•
•
0.04700.0471

33. Theorem (Florian Pausinger, Manas Rachh, S.)
Among all splittings of a domain given by a function y = f (x) with
symmetry around x = y, the following subdivison is optimal.
0.04617

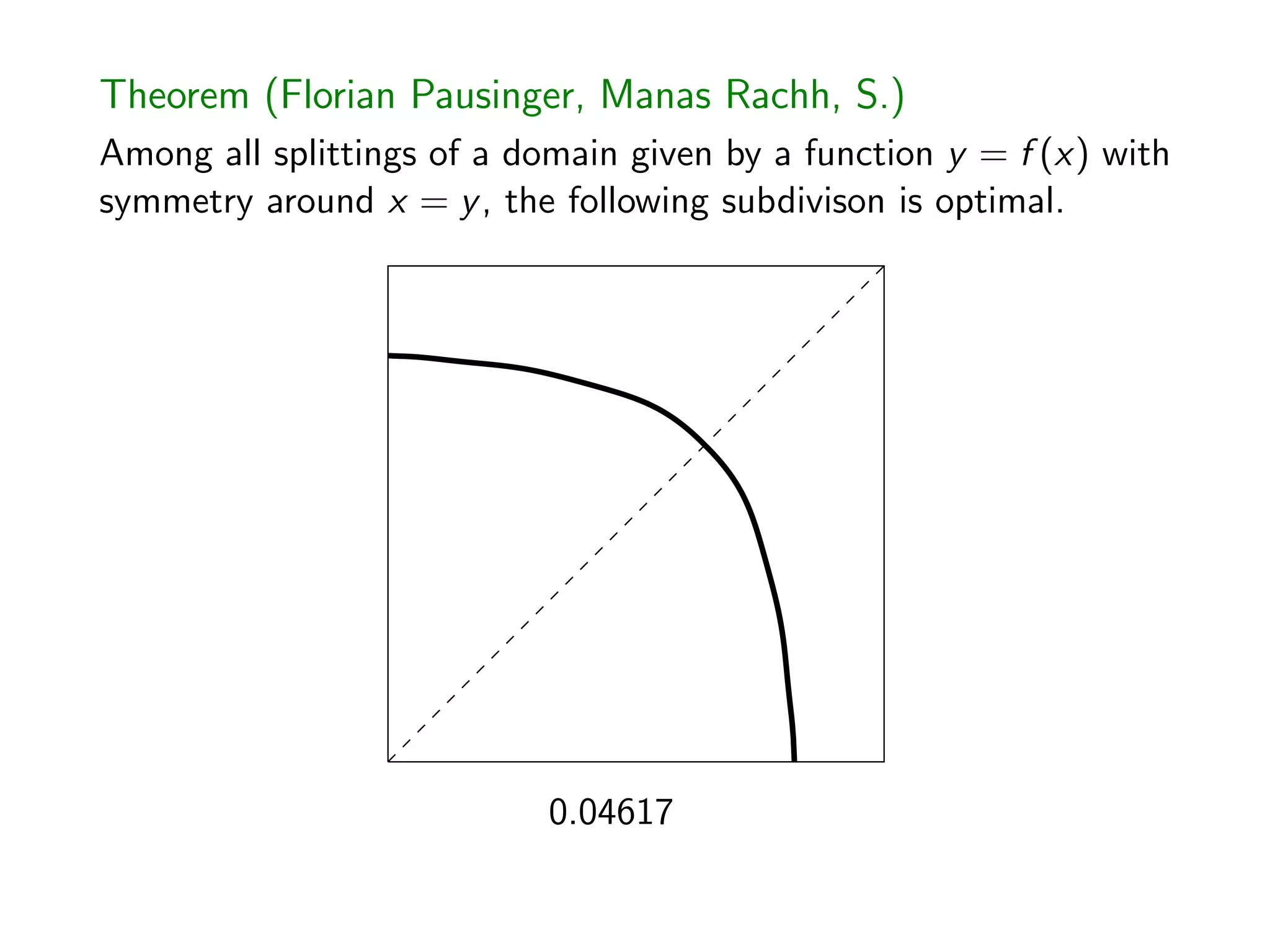
34. The Most Nonlinear Integral Equation I’ve Ever Seen
Theorem (Florian Pausinger, Manas Rachh, S.)
Any optimal monotonically decreasing function g(x) whose graph
is symmetric about y = x satisfies, for 0  x  g 1(0),
(1 2p 4xg(x)) (1 g(x)) + (4p 1)x 1 g(x)2
4
Z g 1(0)
g(x)
(1 y)g (y)dy + g0
(x) (1 2p 4xg(x)) (1 x)
+ (4p 1)g(x) 1 x2
4
Z g 1(0)
x
(1 y)g(y)dy = 0.
Question. How to do 3 points in [0, 1]2? Simple rules?

35. Many thanks!