สถิติสำหรับธุรกิจ

1. ดร.ธีทัต ตรีศิริโชติ

2. สถิติสำหรับธุรกิจ( Statistics For Business )
สถิติ( Statistics ) คือ วิชาที่ว่าด้วยการการเก็บรวบรวมข้อมูลเพื่อนามา
นาเสนอวิเคราะห์เพื่อประโยชน์ในการตัดสินใจในกรณีต่างๆ โดยมี
กระบวนการ 4 ขั้นตอนดังนี้
1. การเก็บรวบรวมข้อมูล
2. การนาเสนอข้อมูล
3. การวิเคราะห์ข้อมูล
4. การตีความข้อมูล
ประโยชน์ของวิชาสถิติ
1. เป็ นสิ่งที่ชี้ให้เห็นข้อเท็จจริงของเหตุกำรณ์และเรื่องรำว
ที่สนใจอยู่
2. เป็ นเครื่องมือในกำรวำงแผนของโครงกำรและกิจกำร
3. เป็ นระเบียบสำหรับกำรวิเครำะห์ในงำนวิจัยโดยทั่วๆไป
4. เป็ นเครื่องมือในกำรประเมินผลของงำนที่ได้ทำไปแล้ว

3. สถิติสำหรับธุรกิจ( Statistics For Business )
ประเภทของข้อมูล( Type of data )
1. ข้อมูลแสดงคุณภำพ ( Qualitative data ) : หมำยถึงข้อมูลที่รวบรวมมำ
โดยพิจำรณำจำกคุณสมบัติของข้อมูลเป็ นหลัก เช่น เพศชำย – หญิง
, สถำนภำพของกำรสมรส โสด แต่ง หม้ำย , ระดับรำยได้ของ
ประชำกร สูง ปำนกลำง ต่ำ
2. ข้อมูลแสดงปริมำณ ( Quantitative data ) : หมำยถึงข้อมูลที่รวบรวม
มำได้ในรูปตัวเลข( Numerical data ) เช่น น้ำหนักของทำรกแรกเกิด
รำยได้ของคนไทย อัตรำเงินเดือน จำนวนนักเรียน

4. สถิติสำหรับธุรกิจ( Statistics For Business )
แหล่งของข้อมูล ( Type of source data )
1. แหล่งทุติยภูมิ ( Secondary source ) : เป็ นแหล่งข้อมูลที่มีกำรบันทึก
ไว้แล้ว เช่น จำนวนนักศึกษำของวิทยำลัยครูนครสวรรค์ ปี
กำรศึกษำ2534 – 2538 ซึ่งเรำจะไปเก็บรวบรวมเองไม่ได้ ซึ่ง
แหล่งข้อมูลประเภทนี้ทำให้เรำทุ่นเวลำ เงินทุน แรงงำน
2. แหล่งปฐมภูมิ ( Primary source ) : เป็ นกำรรวบรวมข้อมูลด้วย
ตนเองเมื่อเรำต้องกำรศึกษำเรื่องใดก็สำมำรถดำเนินกำรได้ด้วย
ตัวเอง

5. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรวิเครำะห์ข้อมูลเบื้องต้น
Measures of Location
• ค่ำเฉลี่ยเลขคณิต ( Mean ) : เป็ นค่ำกลำงที่
นิยมใช้มำกสุดแบ่งออกเป็ น
Population Mean
Sample Mean
ไม่ควรใช้ค่ำMean ในกรณีที่มีOutlier

6. สถิติสำหรับธุรกิจ( Statistics For Business )
2. Median : Md คือ ค่ำตรงกลำงของข้อมูลโดยตำแหน่งโดย
กำรเรียงจำกค่ำมำกไปน้อย หรือ จำกน้อยไปมำก ใช้ในกรณีที่มี
ข้อมูลตัวใดตัวหนึ่งแตกต่ำงจำกกลุ่มข้อมูลหรือ Outlier ถ้ำมี
ข้อมูลตรงกลำง2 ตัวให้นำมำบวกกันแล้วหำร2 จะได้Md
3. Mode : Mo คือค่ำที่เกิดขึ้นซ้ำกันมำกที่สุดซึ่ง Mo สำมำรถมี
ได้หลำยค่ำใช้ได้ดีกับข้อมูลที่เป็ นแบบ Norminal data คือ
ข้อมูลที่ตัวเลขไม่มีควำมสำคัญ เช่น เพศ กำรศึกษำ ศำสนำ

7. สถิติสำหรับธุรกิจ( Statistics For Business )
4. Midrange : Mr คือ กำรหำค่ำกลำงของข้อมูลอย่ำงง่ำยและ
รวดเร็วแต่ไม่ควรใช้ในกรณีที่มี Outlier เพรำะจะเกิดควำม
คลำดเคลื่อนมำก

8. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรวิเครำะห์ข้อมูลเบื้องต้น ( ต่อ )
Measures of Variation
• Mean Absolute Deviation ( MAD ) : เพื่อดูว่ำ
x แตกต่ำงจำก Mean เท่ำไหร่
โดยที่ : MAD น้อย ค่ำแปรผันน้อยมั่นใจว่ำ ถูกต้อง
MAD มำก ค่ำแปรผันมำกมีโอกำสว่ำ ไม่ถูกต้อง

9. สถิติสำหรับธุรกิจ( Statistics For Business )
2. Standard Deviation ( S.D. ) : โดยที่
Population S.D. = σ =
Sample S.D. = S =
เป็ นวิธีที่นิยมใช้ในกำรวัดค่ำควำมผันแปรถ้ำค่ำดังกล่ำวน้อยยิ่งดี
เพรำะข้อมูลไม่มีกำรผันแปร
3. Variance : โดยที่
Population Variance. = σ2
Sample S.D. = S2

10. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรใช้Standard Deviation ในกำรวิเครำะห์ข้อมูล
Chebyshev ’ s Inequality
1. At least 75% of data are between
2. At least 89% of data are between
3. At least of data are between
Empirical Rules
1. About 68% of data are between
2. About 95% of data are between
3. About 99.7% of data are between

11. สถิติสำหรับธุรกิจ( Statistics For Business )
Coefficient of Variation
ถ้ำค่ำที่คำนวณได้ มำก ไม่ดี น้อยดี
ในทำงกำรลงทุนค่ำดังกล่ำวเรียกว่ำ ควำมเสี่ยงต่อ
หนึ่งหน่วยผลตอบแทน

12. สถิติสำหรับธุรกิจ( Statistics For Business )
หมำยถึง มูลที่คำดหวังว่ำจะได้รับโดยปกติในกำรทำธุรกิจ
จะมีผลตอบแทนที่จะได้รับอยู่ 3 กรณีคือ กำไร , เสมอตัว ,
ขำดทุน และโอกำสของแต่ละกรณีย่อมจะไม่เท่ำกัน
สูตร : E(X) = p1x1 + p2x2 + p3x3
P = โอกำสที่จะเกิดขึ้น , X = ผลตอบแทนที่คำดว่ำจะได้รับ

13. สถิติสำหรับธุรกิจ( Statistics For Business )
Probability ( ควำมน่ำจะเป็ น )
m = จำนวนควำมน่ำจะเกิดขึ้นของ A ( Event )
n = จำนวนเหตุกำรณ์ที่อำจเกิดขึ้นได้ทั้งหมด
n เป็ น subset ของ n
ในกรณีนี้ P(A) = 1 แสดงว่ำเหตุกำรณ์นั้นต้องเกิดขึ้นอย่ำงแน่นอน
P(A) = 0 แสดงว่ำเหตุกำรณ์นั้นไม่เกิดขึ้นแน่นอน

14. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : จงหำที่มีคนอย่ำงน้อย 2 คน เกิดวันเดียวกัน
วิธีทำ
P ( 2 คนเกิดวันเดียวกัน ) = 1 – P ( ไม่มี 2 คนใดเกิดวันเดียวกัน )
P ( ไม่มี 2 คนใดเกิดวันเดียวกัน ) =
ถ้ำเลือกคน 2 คนโอกำสที่คน 2 คนเกิดวันเดียวกัน = 1 – 0.997 = 0.003
ถ้ำเลือกคน 23 คนโอกำสที่คน 23 คนเกิดวันเดียวกัน = 1 – 0.49 = 0.51

15. สถิติสำหรับธุรกิจ( Statistics For Business )
Mean
Median
Mode
1. เส้นโค้งปกติจะไม่เบ้
2. เส้นโค้งปกติจะมีรูปคล้ำยระฆังคว่ำ
3. ค่ำเฉลี่ย ( Mean ) , มัธยฐำน( Median )
และฐำนนิยม ( Mode ) ของโค้งปกติจะมี
ค่ำเท่ำกันและจะอยู่ ณ. ตำแหน่งตรง
กลำง

16. สถิติสำหรับธุรกิจ( Statistics For Business )
4. พื้นที่ใต้โค้งปกติทั้งหมด คือ ควำมน่ำจะเป็ น ( Probability )
ของ Sample Space ซึ่งมีค่ำเท่ำกับ 1 หรือ 100% ทุกๆจุด
บนแกนหมำยถึง All possible point ใน Sample Space นั้น
และเนื่องจำกเส้นโค้งมีลักษณะสมมำตรจึงทำให้พื้นที่
ทำงซ้ำยมือและขวำมือเท่ำกันมีพื้นที่ซีกละ 50% ของพื้นที่
ทั้งหมด
5. เส้นโค้งปกติจะมีแกน X เป็ นเส้น asymptote กล่ำวคือปลำย
เส้นโค้งทั้งสองข้ำงจะไม่ตัดกันไม่ว่ำ x จะมีค่ำมำกเท่ำใด

17. สถิติสำหรับธุรกิจ( Statistics For Business )
ลักษณะของเส้นโค้งปกติที่มีµ และσ แตกต่างกัน
µ1  µ2 แต่ σ1 = σ2
µ1 µ2
σ1 σ2
Case I

18. สถิติสำหรับธุรกิจ( Statistics For Business )
ลักษณะของเส้นโค้งปกติที่มี µ และσ แตกต่างกัน
µ1 = µ2 แต่ σ1 < σ2
µ1 = µ2
σ1
σ2
Case II

19. สถิติสำหรับธุรกิจ( Statistics For Business )
ลักษณะของเส้นโค้งปกติที่มี µ และσ แตกต่างกัน
µ1  µ2 แต่ σ1 < σ2
µ1 µ2
σ1 σ2
Case III

20. สถิติสำหรับธุรกิจ( Statistics For Business )
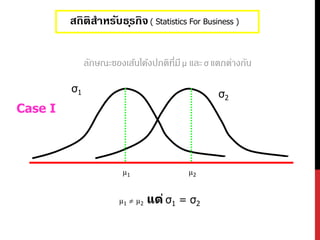
ความเบ้( Skewness ) : ข้อมูลที่มีการแจกแจงแบบ
สมมาตรนั้น Mo , Md , x จะมีค่าเท่ากันหรือทับกันพอดี
ส่วนข ้อมูลที่ไม่สมมาตรคือเบ ้ไปทางซ ้ายหรือขวา
ค่าดังกล่าวจะแตกต่างกันดังนี้
Mo , Md , x X , Md , Mo

21. สถิติสำหรับธุรกิจ( Statistics For Business )
การสอบวิชาสถิติของนิสิต M.BA มี 2 กลุ่มมีผลการสอบดังนี้
กลุ่ม 1 กลุ่ม 2
X = 80
SD = 5
นาย สมรัก สอบได้คะแนน 72
X = 80
SD = 10
นาย สมสมร สอบได้คะแนน 72

22. สถิติสำหรับธุรกิจ( Statistics For Business )
0 2 3-1 1-2-3
Z
พื้นที่การแจกแจงปกติ X
ระหว่าง X = X1 และ X =
X2 ก็จะมีค่าอยู่ระหว่าง z =
z1 และ z = z2 นั่นคือ
ภำษำพูด ภำษำสถิติ

23. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : จงหำค่ำ P ( Z > 1.52 ) = ?
0.4357
0 1.52
P ( Z > 1.52 ) = 0.5 – 0.4357 = 0.0643

24. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : จงหำค่ำ P ( Z > ? ) = 0.643
0.5-0.0643
0
0.0643
ทรำบค่ำพื้นที่ = 0.0643 นำไปหำตำแหน่งจำกตำรำง
โดยนำ 0.5 – 0.0643 = 0.4357
ไปหำค่ำ z ในตำรำงได้= 1.52

25. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : จงหำค่ำ P ( Z < ? ) = 0.1
0.5-0.1
0
0.1
ทรำบค่ำพื้นที่ = 0.1 นำไปหำตำแหน่งจำกตำรำง
โดยนำ 0.5 – 0.1 = 0.4
ไปหำค่ำ z ในตำรำงได้= -1.28

26. สถิติสำหรับธุรกิจ( Statistics For Business )
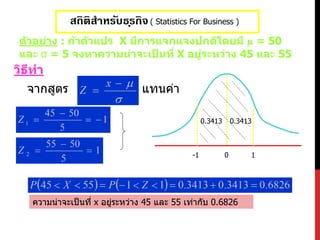
ตัวอย่าง : ถ้าตัวแปร X มีการแจกแจงปกติโดยมี µ = 50
และ σ = 5 จงหาความน่าจะเป็ นที่ X อยู่ระหว่าง 45 และ 55
วิธีทา
จากสูตร แทนค่า
0.3413 0.3413
0-1 1
ความน่าจะเป็นที่ x อยู่ระหว่าง 45 และ 55 เท่ากับ 0.6826

27. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : นักศึกษากลุ่มหนึ่งมีความสูงแจกแจงเป็ นโค้งปกติ ความสูงเฉลี่ย
152 เซนติเมตร ส่วนเบี่ยงเบนมาตราฐาน 4.5 เซนติเมตร จงหาว่ามี
นักศึกษากี่เปอร์เซ็นต์ที่มีความสูง
• ระหว่าง 145 – 155 cm.
• ระหว่าง 150 – 155 cm.
• สูงตั้งแต่ 161 cm ขึ้นไป
• ถ้านักศึกษากลุ่มนี้มี 300 คน จะมีนักศึกษากี่คนที่สูงอยู่ระหว่าง 145 –
155 cm.
วิธีทา
จากสูตร แทนค่า

28. สถิติสำหรับธุรกิจ( Statistics For Business )
• ระหว่าง 145 – 155 cm.
0.4406 0.2486
0-1.56 0.67
ดังนั้นนักศึกษาที่สูงระหว่าง 145 – 155 cm. มีจานวน 68.92%

29. สถิติสำหรับธุรกิจ( Statistics For Business )
• ระหว่าง 150 – 155 cm.
0.1700 0.2486
0-0.44 0.67
ดังนั้นนักศึกษาที่สูงระหว่าง 150 – 155 cm. มีจานวน 41.86%

30. สถิติสำหรับธุรกิจ( Statistics For Business )
• ตั้งแต่ 161 cm. ขึ้นไป
ดังนั้นนักศึกษาที่สูงตั้งแต่ 161 cm. ขึ้นไปมีจานวน 2.28%
0.4772
0 2
0.0228

31. สถิติสำหรับธุรกิจ( Statistics For Business )
ถ้ำนักศึกษำกลุ่มนี้มี 300 คน จะมีนักศึกษำกี่คนที่สูงอยู่ระหว่ำง 145 – 155 cm.
นักศึกษาที่สูง 145 – 155 cm. 100 คนมีจานวน 68.92 คน
ถ้ามีนักศึกษา 300 คนดังนั้นจะมีคนสูงระหว่าง 145 – 155 cm.
คน
จากคาถามข้อแรกเราคานวณได้ว่านักศึกษาที่สูงระหว่าง 145 – 155 cm. มี
จานวน 68.92% หมายถึง

32. สถิติสำหรับธุรกิจ( Statistics For Business )
U
S
ถ้ำต้องกำรศึกษำกลุ่มประชำกรจะ
เสียเวลำ ค่ำใช้จ่ำยสูงมำกในกำร
เก็บข้อมูล ดังนั้นจึงต้องสุ่ม
ตัวอย่ำงกลุ่มตัวอย่ำงเพื่อใช้เป็ น
ตัวแทนของกลุ่มข้อมูลทั้งหมดใน
กำรพยำกรณ์ คำดเดำ เป็ นต้น
ดังนั้นหำกกลุ่มตัวอย่ำงที่ทำกำร
เก็บรวบรวมไม่ดีจะทำให้กำร
พยำกรณ์หรือกำรคำดหมำยผิดไป

33. สถิติสำหรับธุรกิจ( Statistics For Business )
U
S
เป็ นกำรศึกษำของกลุ่มตัวอย่ำงโดยกำร
เลือกกลุ่มตัวอย่ำงจำกประชำกรที่มี
ค่ำเฉลี่ยเลขคณิต = µ และส่วน
เบี่ยงเบนมำตรำฐำน= σ โดยกลุ่ม
ตัวอย่ำงจะมีค่ำ

34. ตัวอย่ำง : โรงงำนผลิตหลอดไฟแห่งหนึ่ง ผลิตหลอดไฟที่มีอำยุกำรใช้
งำนแจกแจงเป็ นโค้งปกติมีค่ำเฉลี่ยเลขคณิต 800 hr. มีส่วนเบี่ยงเบน
มำตรำฐำน 35 hr. จงหำควำมน่ำจะเป็ นที่กลุ่มตัวอย่ำงหลอดไฟที่สุ่มมำ
25 หลอด จะมีอำยุกำรใช้งำนน้อยกว่ำ 780 hr.
วิธีทำ
เนื่องจำกตัวอย่ำงระบุว่ำกำรแจกแจงของประชำกรเป็ นโค้งปกติโดยมี
สถิติสำหรับธุรกิจ( Statistics For Business )
ความน่าจะเป็นที่กลุ่มตัวอย่างจะมีอายุการใช้งานเฉลี่ยน้อยกว่า 780 hr. เท่ากับ 0.0021

35. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : ถ้าค่าเฉลี่ยและส่วนเบี่ยงเบนมาตราฐานของค่าซีรัมเหล็ก ( Serum Iron )
สาหรับบุคคลที่มีสุขภาพแข็งแรงเท่ากับ 120 และ 15 ไมโครกรัมต่อ 100 ml.
ตามลาดับจงหาความน่าจะเป็นที่เลือกได้ตัวอย่างคนที่มีสุขภาพปกติจานวน 50 คน
แล้วมีค่าเฉลี่ยของซีรัมเหล็กระหว่าง 115 และ 125 ไมโครกรัมต่อ 100 ml.
วิธีทำ
ตัวอย่างไม่ได้ระบุลักษณะว่าการกระจายของประชากรเป็นอย่างไรแต่เนื่องจาก
ขนาดของกลุ่มตัวอย่างมากกว่า 30 จึงใช้ทฤษฏี Central Limit
ความน่าจะเป็นที่ได้ค่าเฉลี่ยของซีรัมเหล็กระหว่าง 115 ถึง 125 = P ( 115   125 )

36. สถิติสำหรับธุรกิจ( Statistics For Business )
ดังนั้นความน่าจะเป็นที่ได้คือ 0.9818

37. สถิติสำหรับธุรกิจ( Statistics For Business )
การแจกแจงของผลต่างของค่าเฉลี่ย
ถ ้าประชากร 2 กลุ่มมีค่าเฉลี่ยเป็น µ1 , µ2 และความ
แปรปรวน σ1
2 , σ2
2 ตามลาดับและให ้ เป็นค่าเฉลี่ยของ
กลุ่มตัวอย่างขนาด n1 ที่มาจากการสุ่มประชากรชุดแรก
เป็นค่าเฉลี่ยของกลุ่มตัวอย่างขนาด n2 ที่มาจากการสุ่ม
ประชากรชุดสอง ซึ่งการสุ่มตัวอย่างที่เป็นอิสระทั้งสอง
กลุ่มนี้ว่า การแจกแจงแบบสุ่ม ( Sampling Distribution ) ของ
ค่าสถิติ

38. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : สมมติว่าเวลาโดยเฉลี่ยที่นายแพทย์ผู้หนึ่งใช้ตรวจคนไข้ที่เป็นโรคอย่าง
หนึ่งเท่ากับ 50 นาทีและส่วนเบี่ยงเบนมาตราฐาน 15 นาที ถ้านายแพทย์คน
เดียวกันใช้เวลาโดยเฉลี่ยตรวจโรคคนไข้ซึ่งป่ วยเป็นอีกโรคหนึ่งเท่ากับ 35 นาทีมี
ส่วนเบี่ยงเบนมาตราฐานเท่ากับ 20 นาที ถ้าสุ่มตัวอย่างคนไข้ซึ่งป่ วยด้วยโรคชนิด
แรกมา 36 คน และ ป่ วยด้วยโรคที่สองมา 49 คน จงหาความน่าจะเป็ นที่
ระยะเวลาโดยเฉลี่ยในการตรวจคนไข้ทั้งสองจะแตกต่างกันมากกว่า 20 นาที
วิธีทา
ตัวอย่างไม่ได้ระบุลักษณะว่าการกระจายของประชากรเป็นอย่างไรแต่
เนื่องจากขนาดของกลุ่มตัวอย่างมากกว่า 30 จึงใช้ทฤษฏี Central Limit
ดังนั้น มีการแจกแจงใกล้เคียงเส้นโค้งปกติซึ่งมีค่าเฉลี่ย

39. สถิติสำหรับธุรกิจ( Statistics For Business )
ความแปรปรวน
จากสูตร

40. สถิติสำหรับธุรกิจ( Statistics For Business )
ความน่าจะเป็นที่ระยะเวลาโดยเฉลี่ยในการตรวจคนไข้ทั้งสองโรคจะต่างกัน
มากกว่า 20 นาที = 0.0934

41. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรแจกแจงของสัดส่วน ( Proportion )
ในการทดลองบางครั้งจะมีเหตุการณ์เกิดขึ้น 2 อย่างคือเหตุการณ์ที่
ต้องการหรือไม่ต้องการซึ่งมีลักษณะเป็นสัดส่วนร้อยละ เช่น สุ่มตัวอย่าง
ประชากรมา 100 คนมีคนสูบบุหรี่ 38 คนที่เหลือไม่สูบบุหรี่ลักษณะ
ดังกล่าวเราเรียกว่าสัดส่วนโดยจะสามารถหาค่า z ได้ดังนี้

42. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรแจกแจงผลต่ำงของสัดส่วน
ในการทดลองบางครั้งเราอาจสนใจศึกษาผลต่างของสัดส่วนจาก
ประชากร 2 กลุ่ม p1 – p2 เมื่อ p1 และ p2 คือค่าสัดส่วนจากกลุ่ม
ประชากรทั้งสองกลุ่มโดยสามารถหาคานวณหาค่า z ได้ดังนี้

43. สถิติสำหรับธุรกิจ( Statistics For Business )
การประมาณค่าเป็ นช่วง ( Interval Estimation )
การประมาณค่าเป็นช่วงคือการหาช่วงที่จะประมาณค่าซึ่งประกอบด ้วย
2 ขอบเขตคือ Lower Limit และ Upper Limit เมื่อเราคานวณ
ค่าพารามิเตอร์โดยใช ้ค่าสถิติแล ้วเราจะเชื่อได ้ว่าค่าพารามิเตอร์ที่เรา
ต ้องการจะมีค่าตกอยู่ในช่วงขอบเขตที่อาจจะแคบหรือกว ้างเพียงใดก็
ได ้
ตัวอย่าง : ถ ้าเราต ้องการประมาณอายุเฉลี่ยของนักศึกษาปริญญาตรีโดยทาการสุ่ม
จากนักศึกษาจานวน 100 คนได ้ค่าเฉลี่ย 22 ปีถ ้าเราทาการประมาณค่าเป็นช่วงว่า
คนที่จบปริญญาตรีจะมีอายุระหว่าง
ช่วง 1 : 1 ปี – 100 ปี จะเห็นว่าช่วง 1 มีความถูกต ้อง 100%
ช่วง 2 : 10 ปี – 50 ปี สาหรับช่วงนี้แคบกว่าช่วง 1 ดังนั้นโอกาสถูกต ้องลดลง
ช่วง 3 : 15 ปี – 30 ปี ช่วงนี้ยิ่งแคบขึ้นมีโอกาสถูกต ้องลดลง

44. สถิติสำหรับธุรกิจ( Statistics For Business )
Confidence Interval ( กลุ่มประชากรเดียว )
n > 30 n < 30
รู้ σ รู้ s

45. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : ในกำรสุ่มตัวอย่ำงร้ำนตัดเสื้อสตรีมำ 100 ร้ำนปรำกฏว่ำมี
รำยได้เฉลี่ยเดือนละ 18,000 บำท ส่วนเบี่ยงเบนมำตรำฐำน 3,000
บำท จงหำช่วงควำมเชื่อมั่น 95 % ของรำยได้เฉลี่ยของร้ำนตัดเสื้อสตรี
วิธีทำ
เนื่องจากเราไม่ทราบการแจกแจงของประชากรและกลุ่มตัวอย่างมีขนาดใหญ่
แต่ไม่ทราบความแปรปรวนของประชากรจึงต้องคานวณหาช่วงความเชื่อมั่น
ของรายได้เฉลี่ยจากสูตร

46. สถิติสำหรับธุรกิจ( Statistics For Business )
จากโจทย์ = 18,000 บาท S = 3,000 บาท และ n = 100
 = 1- 0.95 = 0.05  /2 = 0.025 จากตารางจะได้
ดังนั้นช่วงความมั่นใจ 95% ของรายได้เฉลี่ยของร้านตัดเสื้อสตรีอยู่
ระหว่าง 17,412 บาทถึง 18,588 บาท

47. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : กำรกระจำยของปริมำณน้ำหวำนที่บรรจุขวดจำกเครื่อง
อัตโนมัติกระจำยเป็ นโค้งปกติ มีส่วนเบี่ยงเบนมำตรำฐำน 0.5 ออนซ์ จง
ประมำณว่ำปริมำณน้ำหวำนที่บรรจุขวดโดยเฉลี่ยแล้วจะเป็ นเท่ำใด โดยใช้
ช่วงควำมเชื่อมั่น 99% ถ้ำสุ่มตัวอย่ำงน้ำหวำนมำ 36 ขวดและหำปริมำณ
น้ำหวำนเฉลี่ยได้เท่ำกับ 7.4 ออนซ์
วิธีทำ
เนื่องจากการแจกแจงของประชากรเป็นโค้งปกติและทราบส่วนเบี่ยงเบน
มาตราฐานของประชากรจึงคานวณหาช่วงความเชื่อมั่นของปริมาณน้าหวานที่
บรรจุในขวดเฉลี่ยจากสูตร

48. สถิติสำหรับธุรกิจ( Statistics For Business )
จากโจทย์ = 7.4 ออนซ์ σ = 0.5 ออนซ์ และ n = 36
กาหนดช่วงความเชื่อมั่น 99% ดังนั้น
 = 1- 0.99 = 0.01 /2 = 0.005 จากตารางจะได้

49. สถิติสำหรับธุรกิจ( Statistics For Business )
ดังนั้นช่วงความเชื่อมั่น 99% ของปริมาณน้าหวานที่บรรจุขวดโดย
เฉลี่ยอยู่ระหว่าง 7.19 ออนซ์ ถึง 7.61 ออนซ์

50. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : จำกกำรสอบถำมแม่บ้ำน 16 คนที่เลือกมำจำกแม่บ้ำน
ทั้งหมดที่อำศัยอยู่ในหมู่บ้ำนจัดสรรแห่งหนึ่งที่ดูภำพยนต์ก่อนรำยกำร
ข่ำวทำงโทรทัศน์ ปรำกฏว่ำได้ค่ำเฉลี่ยเป็ น 25 วัน ส่วนเบี่ยงเบน
มำตรำฐำน 2 วันจงหำช่วงควำมเชื่อมั่น 90% ของ µ ถ้ำประชำกรมี
กำรแจกแจงปกติ
วิธีทำ
เนื่องจากการแจกแจงของประชากรเป็นโค้งปกติแต่ไม่ทราบความแปรปรวน
ของประชากรและกลุ่มตัวอย่างมีขนาดเล็กจึงต้องคานวณหาช่วงความเชื่อมั่น
ของรายได้เฉลี่ยจากสูตร

51. สถิติสำหรับธุรกิจ( Statistics For Business )
จากโจทย์ = 25 วัน S =2 วัน และ n = 16 , df = n-1 = 15
กาหนดช่วงความเชื่อมั่น 90% ดังนั้น
 = 1- 0.90 = 0.1 /2 = 0.05 จากตารางจะได้

52. สถิติสำหรับธุรกิจ( Statistics For Business )
ดังนั้นช่วงความเชื่อมั่น 90% ของ µ โดยเฉลี่ยอยู่ระหว่าง 24.1235
วัน ถึง 25.8765 วัน

53. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : ในกำรสำรวจต้นโพธิ์ที่มีอำยุ4 ปี มำ 17 ต้นพบว่ำลำต้นถั่ว
เฉลี่ยกว้ำงเท่ำกับ 11.3 นิ้วและส่วนเบี่ยงเบนมำตรำฐำน 3.4 นิ้วจง
ประมำณช่วงควำมเชื่อมั่น 99% ว่ำต้นโพธิ์ที่มีอำยุเฉลี่ย 4 ปี น่ำจะมีลำ
ต้นกว้ำงเท่ำไร ถ้ำสมมติว่ำกำรแจกแจงของประชำกรเป็ นโค้งปกติ
วิธีทำ
เนื่องจากการแจกแจงของประชากรเป็นโค้งปกติและกลุ่มตัวอย่างมีขนาดเล็ก
และไม่ทราบส่วนเบี่ยงเบนมาตราฐานของประชากรจึงต้องคานวณหาช่วงความ
เชื่อมั่นจากสูตร

54. สถิติสำหรับธุรกิจ( Statistics For Business )
จากโจทย์ = 11.3 นิ้ว S =3.4 นิ้ว และ n = 17 , df = n-1 = 16
กาหนดช่วงความเชื่อมั่น 99% ดังนั้น
 = 1- 0.99 = 0.01  /2 = 0.005 จากตารางจะได้

55. สถิติสำหรับธุรกิจ( Statistics For Business )
ดังนั้น ต้นโพธิ์ที่มีอายุ 4 ปีมีลาต้นกว้างระหว่าง 8.89 นิ้ว ถึง
13.71 นิ้วด้วยระดับความเชื่อมั่น 90%

56. สถิติสำหรับธุรกิจ( Statistics For Business )
Confidence Interval ( กลุ่มประชากร 2 กลุ่ม )
1. ถ ้าจานวนประชากรทั้ง 2 กลุ่ม มากกว่า 30 และรู้ค่า σ
2. ถ ้าจานวนประชากรทั้ง 2 กลุ่ม มากกว่า 30 และไม่รู้ค่า σ แต่รู้ค่า s

57. สถิติสำหรับธุรกิจ( Statistics For Business )
3. ถ ้าจานวนประชากรของทั้งสองกลุ่มหรือกลุ่มใดกลุ่มหนึ่งน้อยกว่า 30
และไม่ทราบความแปรปรวนของกลุ่มประชากรทั้งสอง การหาช่วงความเชื่อมั่นของ จะมี 2
แบบดังนี้ ต ้องหาค่า SP
3.1 เมื่อความแปรปรวนของประชากรทั้งสองกลุ่มเท่ากัน หรือ
แต่ไม่ทราบค่าเราสามารถประมาณค่า จาก ได ้จากสูตร

58. สถิติสำหรับธุรกิจ( Statistics For Business )
3.2 เมื่อความแปรปรวนของประชากรทั้งสองกลุ่มไม่เท่ากัน
เมื่อใช ้ และ แทน และ จะได ้

59. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : ในโรงงำนผลิตรถยนต์แห่งหนึ่งต้องกำรศึกษำว่ำอำยุกำรใช้
งำนถั่วเฉลี่ยของไฟหน้ำรถที่ผลิตจำกโรงงำน A และ B จะแตกต่ำงกัน
มำกน้อยเพียงใด จึงสุ่มหลอดไฟจำกโรงงำน A มำ 150 หลอดและมำ
ทดลองใช้ดูพบว่ำมีอำยุกำรใช้งำนถั่วเฉลี่ย 1,400 ชั่วโมง และโรงงำน
A ได้กำหนดส่วนเบี่ยงเบนมำตรำฐำนของประชำกรไว้ 120 ชั่วโมง ใน
ขณะเดียวกันก็สุ่มหลอดไฟโรงงำน B มำ 100 หลอด ทำกำรศึกษำ
พบว่ำอำยุกำรใช้งำนถั่วเฉลี่ย 1,200 ชั่วโมง ส่วนเบี่ยงเบนมำตรำฐำน
ของประชำกร 80 ชั่วโมงจงประมำณช่วงควำมแตกต่ำงของอำยุกำรใช้
งำนโดยเฉลี่ยของหลอดไฟที่ผลิตจำกโรงงำน A และโรงงำน B โดยให้มี
ระดับควำมเชื่อมั่น 95%
วิธีทำ

60. สถิติสำหรับธุรกิจ( Statistics For Business )
จำกโจทย์กำหนด
จำกตำรำง
จะได้ช่วงควำมมั่นใจ

61. สถิติสำหรับธุรกิจ( Statistics For Business )
หมายความว่า ความแตกต่างของอายุการใช้งานถั่วเฉลี่ยของหลอดไฟที่ผลิตจาก
โรงงาน A และ B จะอยู่ระหว่าง 175 hr. ถึง 225 hr. ที่ระดับความเชื่อมั่น 95%

62. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : แบบทดสอบวิชำคณิตศำสตร์ชุดหนึ่งเมื่อเอำไปสอบนักเรียนชำย
49 คนและนักเรียนหญิง 64 คน ปรำกฏว่ำนักเรียนชำยสอบได้คะแนนเฉลี่ย
74 คะแนนส่วนเบี่ยงเบนมำตรำฐำน 6 คะแนนนักเรียนหญิงได้คะแนนเฉลี่ย
65 คะแนนส่วนเบี่ยงเบนมำตรำฐำน 8 คะแนนจงประมำณช่วงควำม
เชื่อมั่น 99% ของผลต่ำงของคะแนนเฉลี่ยนักเรียนชำยและนักเรียนหญิง
วิธีทำ
เนื่องจากกลุ่มตัวอย่างเกิน 30 และไม่ทราบความแปรปรวนของประชากรจึง
ประมาณค่าจากการแจกแจงแบบ Z โดยใช้สูตร

63. สถิติสำหรับธุรกิจ( Statistics For Business )
จำกโจทย์กำหนด
จำกตำรำง
จะได้ช่วงควำมมั่นใจ 99% ของ

64. สถิติสำหรับธุรกิจ( Statistics For Business )
หมายความว่า ความแตกต่างของคะแนนเฉลี่ยของนักเรียนชายและนักเรียนหญิงอยู่
ระหว่าง 5.61 คะแนน ถึง 12.39 คะแนน ที่ระดับความเชื่อมั่น 99%

65. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : ถ้ำกำหนดให้กลุ่มตัวอย่ำง 2 กลุ่มมีขนำด n1 = 25 และ
n2 = 16 จำกประชำกรที่มีกำรแจกแจงปกติ ซึ่งเป็ นอิสระจำกกันและมี
ควำมแปรปรวนเท่ำกันโดยมี X1 = 50 , X2 = 63 , S1 = 6 และ S2 = 5 จง
ประมำณช่วงควำมเชื่อมั่น 95% สำหรับ µ1 - µ2
วิธีทำ
เนื่องจากการแจกแจงของประชากรเป็นโค้งปกติและกลุ่มตัวอย่างมีขนาดเล็ก
และไม่ทราบความแปรปรวนของประชากรจึงต้องคานวณหาช่วงความเชื่อมั่น
จากสูตร

66. สถิติสำหรับธุรกิจ( Statistics For Business )
เมื่อ
จำกตำรำง

67. สถิติสำหรับธุรกิจ( Statistics For Business )
จะได้ช่วงควำมมั่นใจ 95% ของ

68. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : จำกกำรสำรวจค่ำใช้จ่ำยเฉลี่ยต่อวันของนักเรียน โดยสุ่ม
นักเรียนมัธยมปลำยและมัธยมต้นมำ 15 และ 12 คนตำมลำดับ ปรำกฏ
ว่ำนักเรียนชั้นมัธยมศึกษำตอนปลำยใช้จ่ำยเฉลี่ยวันละ 20 บำท ส่วน
เบี่ยงเบนมำตรำฐำน 10 บำท ส่วนนักเรียนชั้นมัธยมศึกษำตอนต้นใช้จ่ำย
วันละ 13 บำทส่วนเบี่ยงเบนมำตรำฐำน 5 บำท ถ้ำค่ำใช้จ่ำยของนักเรียน
ทั้งสองระดับมีกำรแจกแจงใกล้โค้งปกติแต่มีควำมแปรปรวนไม่เท่ำกัน จง
ประมำณช่วงของผลต่ำงของค่ำใช้จ่ำยเฉลี่ยของนักเรียนทั้งสองระดับนี้
โดยใช้ระดับควำมเชื่อมั่น 99%
วิธีทำ
เนื่องจากการแจกแจงของประชากรเป็นโค้งปกติและกลุ่มตัวอย่างมีขนาดเล็ก
และไม่ทราบความแปรปรวนของประชากรจึงต้องคานวณหาช่วงความเชื่อมั่น
จากสูตร

69. สถิติสำหรับธุรกิจ( Statistics For Business )
เมื่อ และ เป็นค่าใช้จ่ายต่อวันของนักเรียนมัธยมปลายและมัธยมต้นตามลาดับ
Degree of freedom หาได้จาก

70. สถิติสำหรับธุรกิจ( Statistics For Business )
แทนค่า

71. สถิติสำหรับธุรกิจ( Statistics For Business )
จำกตำรำง
จะได้ช่วงควำมมั่นใจ 99% ของ

72. สถิติสำหรับธุรกิจ( Statistics For Business )
การประมาณค่าเป็ นช่วงของสัดส่วน 1 กลุ่ม
การประมาณช่วงผลต่างของสัดส่วน

73. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรประมำณช่วงของสัดส่วน
ตัวอย่ำง : บริษัทผลิตผงซักฟอกยี่ห้อหนึ่ง สุ่มตัวอย่ำงผู้ใช้ผงซักฟอกมำ
100 คนเพื่อสอบถำมว่ำชอบผงซักฟอกยี่ห้อนี้หรือไม่ ปรำกฏว่ำชอบ 47
คน จงประมำณช่วงควำมเชื่อมั่น 95% สำหรับสัดส่วนของผู้ที่ชอบ
ผงซักฟอกยี่ห้อนี้
วิธีทำ
จากโจทย์
จะได้ช่วงควำมมั่นใจ 95% สำหรับสัดส่วนของที่ชอบผงซักฟอกยี่ห้อนี้คือ

74. สถิติสำหรับธุรกิจ( Statistics For Business )
ช่วงความเชื่อมั่น 95% สาหรับสัดส่วนของผู้ชอบผงซักฟอก
ชนิดนี้อยู่ระหว่าง 0.37 ถึง 0.57

75. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : ก.ท.ม ต้องกำรประมำณว่ำกี่เปอร์เซ็นต์ของครอบครัวที่อยู่ใน
ก.ท.ม ที่มีรถยนต์ใช้มำกกว่ำ 1 คัน จึงสุ่มตัวอย่ำงมำ 1,000 ครอบครัว
พบว่ำ 425 ครอบครัวมีรถใช้มำกกว่ำ 1 คัน จงประมำณค่ำ p โดยใช้ช่วง
ควำมมั่นใจ 98%
วิธีทำ
จากโจทย์
จะได้ช่วงควำมมั่นใจ 98% สำหรับสัดส่วน p คือ

76. สถิติสำหรับธุรกิจ( Statistics For Business )
แสดงว่าครอบครัวในก.ท.ม มีรถใช้มากกว่า 1 คันประมาณ 38.87 ถึง 46.13% ที่
ระดับตวามเชื่อมั่น 98%

77. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรประมำณช่วงผลต่ำงของสัดส่วน
ตัวอย่ำง : ผู้จัดกำรฝ่ ำยผลิตของโรงงำนอุตสำหกรรมขนำดใหญ่แห่ง
หนึ่ง ต้องกำรประเมินผลเครื่องจักรที่ใช้อยู่ในโรงงำน 2 คือ A และ B โดย
พิจำรณำจำกผลิตภัณฑ์ที่ไม่ได้มำตรำฐำน ซึ่งโรงงำนทั้ง 2 ผลิตได้จำก
กำรทดลองสุ่มตัวอย่ำงผลิตภัณฑ์ที่ผลิตจำกโรงงำนทั้งสองแห่งๆละ
400 ชิ้นปรำกฏว่ำพบผลิตภัณฑ์ที่ไม่ได้มำตรำฐำนจำกโรงงำน A และ
โรงงำน B ร้อยละ 6 และ 8 ตำมลำดับจงประมำณผลต่ำงระหว่ำงสัดส่วน
ของผลิตภัณฑ์ที่ไม่ได้มำตรำฐำนจำกโรงงำน A และโรงงำน B โดยใช้ช่วง
ควำมมั่นใจ 95%
วิธีทำ

78. สถิติสำหรับธุรกิจ( Statistics For Business )
ให้ p1 และ p2 เป็นสัดส่วนของผลิตภัณฑ์ที่ไม่ได้มาตราฐานจากโรงงาน A และ
โรงงาน B ตามลาดับ
ให้ และ เป็นสัดส่วนของผลิตภัณฑ์ที่ไม่ได้มาตราฐานของกลุ่มตัวอย่างที่
สุ่มมาจากโรงงาน A และโรงงาน B ตามลาดับ
จะได้ช่วงควำมมั่นใจ 95% สำหรับสัดส่วน p1 – p2 คือ

79. สถิติสำหรับธุรกิจ( Statistics For Business )
ด้วยช่วงความเชื่อมั่น 95% ผลต่างระหว่างสัดส่วนของผลิตภัณฑ์ที่ไม่ได้มาตราฐานจาก
โรงงาน A และ โรงงาน B อยู่ระหว่าง -0.055 และ 0.015

80. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่ำง : จำกกำรสำรวจควำมนิยมในกำรนั่งรถยนต์โดยสำรปรับ
อำกำศของประชำกรที่อำศัยอยู่ในภำคเหนือ และ ภำคตะวันออก พบว่ำ
กลุ่มตัวอย่ำงที่สุ่มมำภำคละ 500 คนชอบนั่งรถโดยสำรปรับอำกำศ
350 คนและ 300 คน ตำมลำดับจงประมำณผลต่ำงของสัดส่วนผู้ที่
นิยมนั่งรถโดยสำรปรับอำกำศที่อำศัยอยู่ในภำคเหนือและภำคตะวันออก
โดยใช้ช่วงควำมเชื่อมั่น 90%
วิธีทำ
ให้ p1 และ p2 เป็นสัดส่วนของผู้นิยมนั่งรถปรับอากาศที่อาศัยอยู่ในภาคเหนือและ
ภาคตะวันออก ตามลาดับ
ให้ และ เป็นสัดส่วนของผู้นิยมนั่งรถปรับอากาศของกลุ่มตัวอย่างที่สุ่มมาจาก
ผู้ที่อาศัยอยู่ในภาคเหนือและภาคตะวันออก ตามลาดับ

81. สถิติสำหรับธุรกิจ( Statistics For Business )
จะได้ช่วงควำมมั่นใจ 95% สำหรับสัดส่วน p1 – p2 คือ

82. สถิติสำหรับธุรกิจ( Statistics For Business )
ด้วยช่วงความเชื่อมั่น 90% ผลต่างระหว่างสัดส่วนผู้ที่นิยมนั่งรถโดยสารปรับอากาศ ที่
อาศัยอยู่ในภาคเหนือและภาคตะวันออกอยู่ระหว่าง 0.05 และ 0.15

83. สถิติสำหรับธุรกิจ( Statistics For Business )
กำรทดสอบสมมติฐำน ( Hypothesis Testing )
การสมมติฐานคือการใช้ข้อมูลจากกลุ่มตัวอย่างมาทดสอบว่าค่าพารามิเตอร์ของ
ประชากรที่เราต้องการทราบเป็ นไปตามความเชื่อที่คิดไว้หรือไม่ ซึ่งความเชื่อนี้
อาจเกิดจากประสบการณ์ ความรู้ ทฤษฏี หรือกฏเกณฑ์ต่างๆความเชื่ออันนี้เรา
เรียกว่า สมมติฐาน ( Hypothesis ) นั่นเองซึ่งอาจจะเป็นจริงหรือเป็นเท็จก็ได้ เช่น
บริษัทผลิตยางรถยนต์ใหม่นี้จะมีอายุการใช้งานเฉลี่ยมากกว่า 25,000 ไมล์ความ
เชื่ออันนี้ก็คือสมมติฐานนั่นเองแต่จะเป็ นจริงหรือไม่ก็ต้องทาการทดสอบต่อไป
โดยการสุ่มตัวอย่างยางรถยนต์ดังกล่าวมาทดลองใช้ การดาเนินการทดสอบแบบ
นี้ เรียกว่า การทดสอบสมมติฐาน ( Hypothesis Testing )

84. สถิติสำหรับธุรกิจ( Statistics For Business )
1. ความคลาดเคลื่อนประเภทที่ 1 ( Type I error ) เป็นความคลาดเคลื่อนที่เกิดขึ้นเมื่อ
สมมติฐานศูนย์ที่เป็นจริงถูกปฏิเสธค่าความน่าจะเป็นที่จะเกิดความคลาดเคลื่อนประเภท
1 กาหนดด้วย 
2. ความคลาดเคลื่อนประเภทที่ 2 ( Type II error ) เป็นความคลาดเคลื่อนที่เกิดขึ้นเมื่อ
สมมติฐานศูนย์ที่เป็นเท็จไม่ถูกปฏิเสธ หรือ เกิดจากการที่เราไปยอมรับสมมติฐานศูนย์
เมื่อสมมติฐานศูนย์เป็นเท็จนั่นเอง ค่าความน่าจะเป็นที่จะเกิดความคลาดเคลื่อนประเภท 2
กาหนดด้วย 

85. สถิติสำหรับธุรกิจ( Statistics For Business )
เพื่อความเข้าใจในความแตกต่างระหว่างความคลาดเคลื่อนทั้งสองชนิด ขอ
ยกตัวอย่างเกี่ยวกับการตัดสินคดีความผิดของศาลดังนี้ สมมติว่านาย ก.
ถูกจับในข้อหาลักทรัพย์ ผู้พิพากษาอาจตั้งสมมติฐานดังนี้
นาย ก. เป็นผู้บริสุทธิ์
นาย ก. มีความผิด
ผู้พิพากษาต้องตัดสินใจเลือกเอาสมมติฐานใดสมมติฐานหนึ่งในสองสมมติฐาน
ถ้าผู้พิพากษาตัดสินใจว่า นาย ก. มีความผิดทั้งที่นาย ก. เป็นผู้บริสุทธิ์ไม่ได้ลัก
ทรัพย์จากผู้ใด ก็แสดงว่าการตัดสินของศาลเกิดความคลาดเคลื่อนประเภท 1 (
Type I error ) เนื่องจากปฏิเสธสมมติฐานที่เป็นจริง

86. สถิติสำหรับธุรกิจ( Statistics For Business )
และถ้าผู้พิพากษาตัดสินใจว่า นาย ก. เป็นผู้บริสุทธิ์ทั้งที่นาย ก. เป็นผู้ลักทรัพย์
จากเขามาจริงๆ ความผิดพลาดในการตัดสินใจชนิดนี้คือความคลาดเคลื่อน
ประเภท 2 ( Type II error ) เนื่องจากไปยอมรับสมมติฐานศูนย์ทั้งที่มันไม่เป็น
ความจริง
ควำมคลำดเคลื่อนประเภท Type I error เป็ นควำมผิดพลำดที่รุนแรง
กว่ำควำมคลำดเคลื่อนประเภท Type II error

87. สถิติสำหรับธุรกิจ( Statistics For Business )
ระดับนัยสาคัญ ( Level of Significance )
คือความน่าจะเป็นในการเกิดความคลาดเคลื่อนประเภท 1 ซึ่งมีค่าเท่ากับ ซึ่ง
ระดับนัยสาคัญนี้ผู้ทาการวิจัยจะต้องกาหนดโดยปกติมักจะให้ค่า  มีค่าน้อยๆ
ตัวอย่างเช่น
= 0.1 หมายความว่า ในจานวน 100 ครั้งที่ผู้วิจัยทดลองจะมี 10 ครั้งที่เกิด
ความคลาดเคลื่อนประเภทที่ 1
ถ้าค่า มีค่าน้อยความเชื่อมั่นก็จะยิ่งมีค่าสูง

88. สถิติสำหรับธุรกิจ( Statistics For Business )
Reject Hypothesis Reject Hypothesis
Accept Hypothesis
Acceptance Region Rejection RegionRejection Region
1 - 
1. ถ้าเราตั้ง และ การหาช่วงสาหรับทดสอบต้องทา 2
ทางการทดสอบแบบนี้เรียกว่าการทดสอบแบบ 2 ทาง ( Two – Tail Test ) ช่วง
ของการยอมรับ ( accept ) และการปฏิเสธ ( reject ) จะเป็นดังนี้

89. สถิติสำหรับธุรกิจ( Statistics For Business )
Reject HypothesisAccept Hypothesis
Acceptance Region Rejection Region
1 - 
2. ถ้าเราตั้ง และ การหาช่วงสาหรับทดสอบต้องทาทาง
เดียวการทดสอบแบบนี้เรียกว่าการทดสอบแบบทางเดียว( One – Tail Test )
ช่วงของการยอมรับ ( accept ) และการปฏิเสธ ( reject ) จะเป็นดังนี้

90. สถิติสำหรับธุรกิจ( Statistics For Business )
Reject Hypothesis Accept Hypothesis
Acceptance RegionRejection Region
1 - 
3. ถ้าเราตั้ง และ การหาช่วงสาหรับทดสอบต้อง
ทาทางเดียวการทดสอบแบบนี้เรียกว่าการทดสอบแบบทางเดียว( One – Tail
Test ) ช่วงของการยอมรับ ( accept ) และการปฏิเสธ ( reject ) จะเป็นดังนี้

91. สถิติสำหรับธุรกิจ( Statistics For Business )
การทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยของประชากรกลุ่มเดียว
1. การทดสอบด้วยค่าสถิติ z ( z test ) มีขั้นตอนดังนี้
- ตั้งสมมติฐาน
- กาหนดระดับความมีนัยสาคัญ
- หาเขตวิกฤต หรือ เขตการปฏิเสธ
- คานวณหาค่าสถิติที่ใช้ในการทดสอบ
- สรุปผล

92. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : จากการวิจัยเกี่ยวกับเรื่องระดับระดับสติปัญญาของกรรมกรที่เคย
วิจัยมาแล้วพบว่ามีระดับสติปัญญาเฉลี่ย 100 คะแนนความแปรปรวน 24 คะแนน
ต้องการศึกษาใหม่ในกลุ่มกรรมกรที่กาลังว่างงาน ว่าจะมีระดับสติปัญญาเฉลี่ย
100 คะแนนด้วยหรือไม่ผู้วิจัยจึงสุ่มตัวอย่างกรรมกรว่างงานมา 40 คนแล้ววัด
ระดับสติปัญญาด้วยเครื่องมือทางจิตวิทยาพบว่ามีระดับสติปัญญาเฉลี่ย 97
คะแนนจงทดสอบระดับสติปัญญาของกรรมกรว่างงานว่าน้อยกว่ากรรมกร
ทั่วไปจริงหรือไม่โดยใช้ระดับนัยสาคัญ 0.05
วิธีทา
1. ตั้งสมมติฐาน

93. 2. กาหนด = 0.05
3. เขตวิกฤต จากตาราง
สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance RegionRejection Region

94. สถิติสำหรับธุรกิจ( Statistics For Business )
4. คานวณหาค่าสถิติจากสูตร
Acceptance RegionRejection Region

95. สถิติสำหรับธุรกิจ( Statistics For Business )
5. สรุปผลเนื่องจากค่า Z ที่คานวณได้ตกอยู่ในเขต Reject จึงต้องปฏิเสธ H0
ไปยอมรับ H1 แสดงว่ากรรมกรที่ว่างงานมีระดับสติปัญญาต่ากว่า 100 ซึ่ง
สนับสนุนสมมติฐานที่ว่ากรรมกรที่ว่างงานจะมีระดับสติปัญญาต่ากว่ากรรมกร
ทั่วๆไปที่ระดับนัยสาคัญ 0.05

96. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : จากแบบทดสอบฉบับหนึ่งระบุค่า norm ว่ามีค่าเฉลี่ยเท่ากับ 80 และมี
ความเบี่ยงเบนมาตราฐานเท่ากับ 12 สุ่มนักเรียนมา 25 คนทาการสอนด้วยวิธี
แบบใหม่ เมื่อสิ้นสุดภาคเรียนแล้วใช้แบบทดสอบฉบับเดียวกันนี้สอบ ปรากฏว่าได้
คะแนนเฉลี่ย 88 จงทดสอบว่าการสอนแบบใหม่มีผลทาให้คะแนนสูงกว่าแบบเก่า
หรือไม่โดยใช้ระดับนัยสาคัญ 0.01
วิธีทา
1. ตั้งสมมติฐาน
2. กาหนด = 0.01
3. เขตวิกฤต จากตาราง

97. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection Region
4. คานวณหาค่าสถิติจากสูตร

98. สถิติสำหรับธุรกิจ( Statistics For Business )
5. สรุปผลเนื่องจากค่า Z ที่คานวณได้ตกอยู่ในเขต Reject จึงต้องปฏิเสธ H0
ไปยอมรับ H1 แสดงว่าการสอนด้วยวิธีแบบใหม่ทาให้คะแนนเฉลี่ยของนักเรียน
สูงขึ้นจริงที่ระดับนัยสาคัญ 0.01

99. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : จงทดสอบสมมติฐานว่า µ = 60 โดยกาหนดให้ σ = 10 , n = 25 และ
คานวณค่า จากกลุ่มตัวอย่างที่สุ่มมาได้ 57 โดยมีค่า α= 0.05
วิธีทา 1. ตั้งสมมติฐาน
2. กาหนด = 0.05
3. เขตวิกฤต จากตาราง
4. คานวณหาค่าสถิติจากสูตร

100. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection RegionRejection Region
5. สรุปผลเนื่องจากค่า Z ที่คานวณได้ตกอยู่นอกเขต Reject จึงยอมรับ H0
แสดงว่า ที่ระดับนัยสาคัญ 0.05

101. สถิติสำหรับธุรกิจ( Statistics For Business )
การทดสอบด้วยค่าสถิติ t ( t – test ) เป็นการทดสอบสมมติฐานเกี่ยวกับ
ค่าเฉลี่ยของประชากรกลุ่มเดียว เมื่อไม่ทราบค่าความแปรปรวนของประชากร
และกลุ่มตัวอย่างมีขนาดเล็ก ( n < 30 ) ทั้งนี้กลุ่มตัวอย่างจะต้องได้มาโดย
การสุ่มเช่นเดียวกัน ค่าสถิติที่ใช้ทดสอบคือ
การทดสอบนั้นมีขั้นตอนแบบเดียวกับ z – test แต่การเปิดตารางใช้ตาราง
แจกแจงแบบ t นั่นเอง

102. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : โรงงานผลิตถ่านไฟฉายแห่งหนึ่งโฆษณาว่าอายุการใช้งานเฉลี่ยของ
ถ่านไฟฉายชนิดนี้เกิน 100 ชั่วโมง ลูกค้ารายหนึ่งต้องการทดสอบคาโฆษณา
ดังกล่าว จึงสุ่มตัวอย่างถ่านไฟฉายมาทดลองใช้ 9 ก้อนได้อายุการใช้งานเป็น
ชั่วโมงดังต่อไปนี้ 100 , 95 , 100 , 92 , 85 , 86 , 95 , 99 , 103 จงทดสอบ
สมมติฐานว่าอายุการใช้งานเฉลี่ยของถ่านไฟฉายนี้มากกว่า 100 ชั่วโมงจริง
หรือไม่ โดยมีค่า α= 0.10
วิธีทา 1. ตั้งสมมติฐาน
2. กาหนด = 0.10
3. เขตวิกฤต จากตาราง

103. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection Region
4. คานวณหาค่าสถิติจากสูตร

104. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection Region

105. สถิติสำหรับธุรกิจ( Statistics For Business )
5. สรุปผลเนื่องจากค่า t ที่คานวณได้ตกอยู่ในเขตการยอมรับ จึงยอมรับ H0
แสดงว่าอายุการใช้งานของถ่านไฟฉายนี้ไม่เกิน 100 ชั่วโมงที่ระดับนัยสาคัญ 0.05

106. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : ข้อสอบมาตราฐานวิชาคณิตศาสตร์ชั้นประถมปีที่ 6 เมื่อนาไปทดสอบ
นักเรียนชั้นประถมปีที่ 6 ที่สุ่มมา 16 คนปรากฏว่าได้คะแนนเฉลี่ย 45 คะแนนส่วน
เบี่ยงเบนมาตราฐาน 5.2 คะแนนเราจะเชื่อได้หรือไม่ว่านักเรียนชั้นประถมปีที่ 6
โดยทั่วๆไปจะสอบข้อสอบมาตราฐานชุดนี้ได้คะแนนเฉลี่ยไม่ถึง 50 คะแนน โดยใช้
ระดับนัยสาคัญ 0.01
วิธีทา
1. ตั้งสมมติฐาน
2. กาหนด = 0.01
3. เขตวิกฤต จากตาราง
เนื่องจากเราไม่ทราบความแปรปรวนของประชากรและกลุ่มตัวอย่างมี
ขนาดเล็ก n = 16 จึงต้องทาการทดสอบสมมติฐานโดยการใช้ t – test

107. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance RegionRejection Region
4. คานวณหาค่าสถิติจากสูตร

108. สถิติสำหรับธุรกิจ( Statistics For Business )
5. สรุปผลเนื่องจากค่า t ที่คานวณได้ตกอยู่ในเขตวิกฤต จึงต้องปฏิเสธ H0 ไป
ยอมรับ H1 แสดงว่านักเรียนชั้นประถมปีที่ 6 โดยทั่วไปสอบข้อสอบมาตราฐานชุด
นี้แล้วได้คะแนนเฉลี่ยไม่ถึง 50 คะแนน ที่ระดับนัยสาคัญ 0.01

109. สถิติสำหรับธุรกิจ( Statistics For Business )
การทดสอบสมมติฐานเกี่ยวกับผลต่างของค่าเฉลี่ยของประชากรสองกลุ่ม
ในการทดสอบสมมติฐานบางครั้งกลุ่มประชากรอาจมีมากกว่า 1 กลุ่มโดยมี
2 กลุ่มซึ่งใช้เปรียบเทียบกันโดยมีตัวอย่างและการคานวณดังนี้

110. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : ต้องการทราบว่านักศึกษารับอนุปริญญาสาขาวิทยาศาสตร์ ( อ.วท
) และ นักศึกษาระดับอนุปริญญา สาขาศิลปศาสตร์ ( อ.ศศ ) มีค่าใช้จ่ายประจา
สัปดาห์โดยเฉลี่ยเท่ากันหรือไม่ จึงได้ทาการสารวจโดยการสุ่มตัวอย่างนักศึกษาทั้ง
สองสาขา มาศึกษาได้ค่าสถิติดังต่อไปนี้
สาขา ขนาดกลุ่มตัวอย่าง ค่าเฉลี่ย ความแปรปรวน
อ.วท. 64 112 16
อ.ศศ. 81 109 25
จงทดสอบว่านักศึกษาทั้งสองสาขานี้มีค่าใช้จ่ายประจาสัปดาห์โดยเฉลี่ยเท่ากัน
หรือไม่ โดยใช้ระดับนัยสาคัญ 0.05
วิธีทา

111. สถิติสำหรับธุรกิจ( Statistics For Business )
1. ตั้งสมมติฐาน
2. กาหนด = 0.05
3. เขตวิกฤต จากตาราง
Acceptance Region Rejection RegionRejection Region

112. สถิติสำหรับธุรกิจ( Statistics For Business )
4. คานวณหาค่าสถิติจากสูตร
5. สรุปผลปฏิเสธ H0 ยอมรับ H1 แสดงว่า นักศึกษา อ.วท. และ อ.ศศ. มีค่าใช้จ่าย
ประจาสัปดาห์โดยเฉลี่ยไม่เท่ากัน ที่ระดับนัยสาคัญ 0.05

113. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : ต้องการเปรียบเทียบวิธีการสอน 2 แบบจึงสุ่มนักเรียนมา 2 กลุ่มกลุ่ม
ละ 50 คน คนกลุ่มแรกทาการสอนแบบเก่า กลุ่มที่ 2 ทาการสอนแบบใหม่เมื่อ
สิ้นสุดการทดลองแล้วทาการทดสอบด้วยมาตราฐานชุดเดียวกัน ปรากฏว่า กลุ่ม
แรกได้คะแนนเฉลี่ย 68 คะแนน ส่วนเบี่ยงเบนมาตราฐาน 5.2 กลุ่มที่ 2 ได้คะแนน
เฉลี่ย 70.5 คะแนน ส่วนเบี่ยงเบนมาตราฐาน 5.8 จงทดสอบสมมติฐานว่าผลการ
สอนแบบใหม่มีคะแนนเฉลี่ยสูงกว่าผลการสอนแบบเก่าจริงหรือไม่ โดยใช้ระดับ
นัยสาคัญ 0.025
วิธีทา
ให้ คะแนนเฉลี่ยของการสอนแบบใหม่
คะแนนเฉลี่ยของการสอนแบบเก่า
1. ตั้งสมมติฐาน

114. สถิติสำหรับธุรกิจ( Statistics For Business )
2. กาหนด = 0.025
3. เขตวิกฤต จากตาราง
Acceptance Region Rejection Region

115. สถิติสำหรับธุรกิจ( Statistics For Business )
4. คานวณหาค่าสถิติจากสูตร
5. สรุปผลปฏิเสธ H0 ยอมรับ H1 แสดงว่าการสอนแบบใหม่ได้คะแนนเฉลี่ยสูงกว่า
การสอนแบบเก่าจริง ที่ระดับนัยสาคัญ 0.025

116. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : ในการทดสอบหลอดไฟสองชนิดว่าชนิดใดมีอายุการใช้งานนานกว่าได้
สุ่มตัวอย่างหลอดไฟชนิดแรกมา 100 หลอดทดลองใช้ดู ปรากฏว่ามีอายุการใช้
งานเฉลี่ย 1,840 ชั่วโมง ส่วนเบี่ยงเบนมาตราฐาน 65 ชั่วโมง สุ่มตัวอย่างหลอดไฟ
ชนิดที่สองมา 81 หลอด ทดลองใช้ดูมีอายุการใช้งานเฉลี่ย 1,490 ชั่วโมง ส่วน
เบี่ยงเบนมาตราฐาน 45 ชั่วโมงจะเชื่อได้หรือไม่ว่าหลอดไฟชนิดแรกมีอายุการใช้งาน
นานกว่าหลอดไฟชนิดที่สองมากกว่า 300 ชั่วโมง โดยใช้ระดับนัยสาคัญ 0.01
วิธีทา
ให้ อายุการใช้งานเฉลี่ยของหลอดไฟชนิดแรก
อายุการใช้งานเฉลี่ยของหลอดไฟชนิดที่สอง
1. ตั้งสมมติฐาน

117. สถิติสำหรับธุรกิจ( Statistics For Business )
2. กาหนด = 0.01
3. เขตวิกฤต จากตาราง
Acceptance Region Rejection Region

118. สถิติสำหรับธุรกิจ( Statistics For Business )
4. คานวณหาค่าสถิติจากสูตร
5. สรุปผลปฏิเสธ H0 ยอมรับ H1 แสดงว่าหลอดไฟชนิดแรกมีอายุการใช้งานนาน
กว่าหลอดไฟชนิดที่สอง เกินกว่า 300 ชั่วโมง ที่ระดับนัยสาคัญ 0.01

119. สถิติสำหรับธุรกิจ( Statistics For Business )
การทดสอบสมมติฐานเกี่ยวกับผลต่างของสัดส่วนของประชากรสองกลุ่ม

120. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : โรงงานผลิตเครื่องใช้พลาสติกแห่งหนึ่งพบว่าผลิตภัณฑ์ที่นา
ออกจาหน่ายนั้นเมื่อถูกความร้อนบางชิ้นจะเปลี่ยนสีไป จึงคิดจะใช้การผลิต
แบบใหม่ ซึ่งทางโรงงานไม่แน่ใจว่าจะดีจริงหรือไม่ จึงทาการทดสอบโดยการ
สุ่มตัวอย่างเครื่องใช้ไฟฟ้ าที่ผลิตโดยวิธีเก่ามา 1,500 ชิ้น พบว่ามีสีเปลี่ยนไป
105 ชิ้น และสุ่มตัวอย่างเครื่องใช้ที่ผลิตโดยวิธีใหม่มา 2,000 ชิ้น พบว่ามีสี
เปลี่ยนไป 80 ชิ้น จงทดสอบว่าวิธีการผลิตแบบใหม่ให้ผลผลิตดีกว่าแบบเก่า
หรือไม่ โดยใช้ระดับนัยสาคัญ 0.05
วิธีทา ให้ สัดส่วนผลิตภัณฑ์ที่เปลี่ยนสีจากการผลิตโดยวิธีเก่า
สัดส่วนผลิตภัณฑ์ที่เปลี่ยนสีจากการผลิตโดยวิธีใหม่

121. สถิติสำหรับธุรกิจ( Statistics For Business )
1. ตั้งสมมติฐาน
2. กาหนด = 0.05
3. เขตวิกฤต จากตาราง

122. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection Region

123. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection Region

124. สถิติสำหรับธุรกิจ( Statistics For Business )
5. สรุปผลปฏิเสธ H0 ยอมรับ H1 แสดงว่าสัดส่วนของผลิตภัณฑ์ที่เปลี่ยนสีที่ผลิต
โดยวิธีเก่ามากกว่าวิธีใหม่ จึงแน่ใจได้ว่าวิธีผลิตแบบใหม่ให้ผลดีกว่าวิธีเก่า ที่ระดับ
นัยสาคัญ 0.05

125. สถิติสำหรับธุรกิจ( Statistics For Business )
ตัวอย่าง : พรรคการเมืองหนึ่งต้องการทราบเสียงสนับสนุนพรรคในเขต
เลือกตั้งที่อยู่ในเมืองและในชนบท จึงสุ่มตัวอย่างผู้มีสิทธิ์ออกเสียง
เลือกตั้งมาสัมภาษณ์ เพื่อทราบเสียงสนับสนุน ปรากฏว่าในเมืองมีเสียง
สนับสนุน 180 เสียง จากกลุ่มตัวอย่างจานวน 300 คน และในชนบทมี
เสียงสนับสนุน 240 เสียง จากกลุ่มตัวอย่างจานวน 500 คน จงทดสอบ
โดยใช้ระดับนัยสาคัญ 0.25 ว่าในการเลือกตั้งจริงนั้น
1. เสียงสนับสนุนในเมืองมากกว่าในชนบท
2. เสียงสนับสนุนในเมืองมากกว่าในชนบทเกินกว่า 5%
วิธีทา
เสียงสนับสนุนในเมืองมำกกว่ำในชนบท

126. สถิติสำหรับธุรกิจ( Statistics For Business )
ให้ เป็นสัดส่วนของเสียงสนับสนุนในเมือง
เป็นสัดส่วนของเสียงสนับสนุนในชนบท
1. ตั้งสมมติฐาน
2. กาหนด = 0.025
3. เขตวิกฤต จากตาราง

127. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection Region

128. สถิติสำหรับธุรกิจ( Statistics For Business )
5. สรุปผลปฏิเสธ H0 ยอมรับ H1 แสดงว่าในการเลือกตั้งจริงสัดส่วนของเสียง
สนับสนุนพรรคการเมืองนี้ในเมืองจะมากกว่าเสียงสนันสนุนในชนบท ที่ระดับ
นัยสาคัญ 0.025

129. สถิติสำหรับธุรกิจ( Statistics For Business )
เสียงสนับสนุนในเมืองมำกกว่ำในชนบทเกินกว่ำ 5%
1. ตั้งสมมติฐาน
2. กาหนด = 0.025
3. เขตวิกฤต จากตาราง

130. สถิติสำหรับธุรกิจ( Statistics For Business )
Acceptance Region Rejection Region

131. สถิติสำหรับธุรกิจ( Statistics For Business )
5. สรุปผลยอมรับ H0 แสดงว่าในการเลือกตั้งจริงสัดส่วนของเสียงสนับสนุน
พรรคการเมืองนี้ในเมืองจะมากกว่าเสียงสนันสนุนในชนบทไม่เกิน 5% ที่ระดับ
นัยสาคัญ 0.025

132. จบแล้วครับ