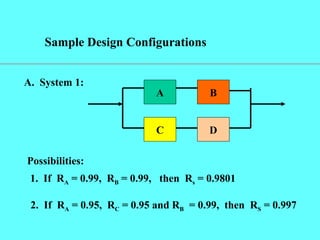
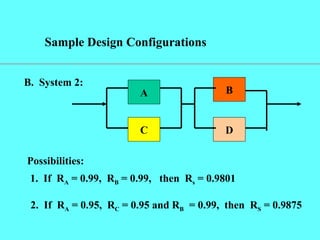
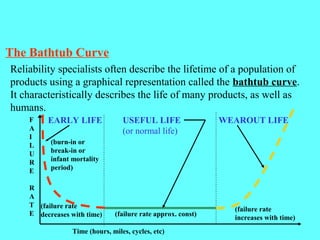
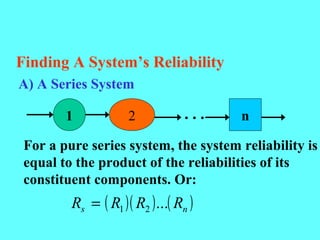
This document discusses reliability and its importance. It defines reliability as the probability that a system will work, and provides examples of calculating reliability for series and parallel systems. Key points made include: - Reliability measures the likelihood a system will function and is important for reputation, customer satisfaction, costs and competitive advantage. - The reliability of a series system is the product of the component reliabilities, while the reliability of a parallel system is 1 minus the product of the component unreliabilities. 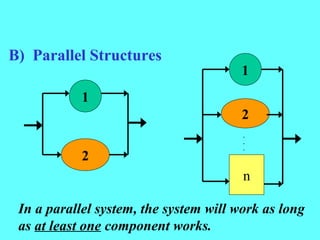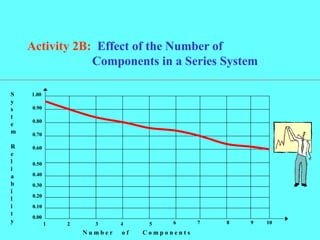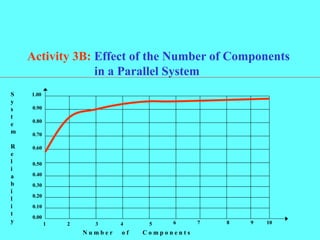- More components in a series system lowers the overall reliability, while more components in a parallel system increases the overall reliability. 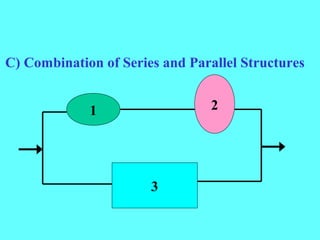- Complex systems can combine series and parallel components, requiring multi-step calculations to

1. Reliability
Dr. Munthear Alqaderi
munthear@gmail.com
Mobile: 0096893569971

2. What is reliability?
Reliability measures the probability that a
system or part of a system will work.
So, if I say that the reliability of my walkman is
0.98 (or 98%), I mean that my walkman is
working 98% of the time and failing 2% of the
time.

3. Why is Reliability Important?
• Reputation
• Customer Satisfaction
• Warranty Costs
•Cost Analysis
•Customer Requirements
• Competitive Advantage

4. What is a system?
A system is a collection of components, subsystem
and/or assemblies arranged to a specific design
in order to achieve desired functions with acceptable
performance and reliability.

5. Models of a System
A) Series Structures
1 2
For this system to work, both components 1
and 2 must work.
1 2 . . . n
In this case, all n components must work in
order for the whole system to work.

6. A Personal Computer
Power
Supply
Motherboard
Processor
Hard
Drive
A Simple Series system

7. B) Parallel Structures
1
2
1
2
.
.
.
n
In a parallel system, the system will work as long
as at least one component works.

8. C) Combination of Series and Parallel Structures
1 2
3

9. Finding A System’s Reliability
1 2 n. . .
A) A Series System
For a pure series system, the system reliability is
equal to the product of the reliabilities of its
constituent components. Or:
( )( ) ( )ns RRRR ...21=

10. Example:
Three components are connected in series and make
up a system. Component 1 has a reliability of 0.95,
component 2 has a reliability of 0.98 and
component 3 has a reliability of 0.97 for a mission
of 100 hours. Find the overall reliability of the
system for a 100-hr mission.
Solution:
= (0.95)(0.98)(0.97)
= 0.90 = 90%
Rs = (R1)(R2)(R3)

11. Activity 2A: Computing Series System’s
Reliability
0.8
1)
0.9 Rs = (0.8)(0.9)
= 0.72
2)
0.7 0.6
Rs = (0.7)(0.6)
= 0.42

12. Activity 2B: Effect of the Number of
Components in a Series System
S
y
s
t
e
m
R
e
l
i
a
b
i
l
i
t
y
1.00
0.90
0.80
0.70
0.60
0.50
0.40
0.30
0.20
0.10
0.00
1 2 3 4 5 6 7 8 9 10
N u m b e r o f C o m p o n e n t s

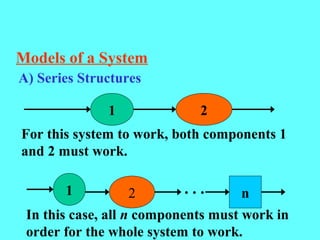
13. B) A Parallel System
1
2
n
.
.
.
For a pure parallel system,
the overall system reliability
is equal to the product of the
component unreliabilities.
Thus, the reliability of the
parallel system is given by:
Rs = 1 – [(1 – R1)(1-R2)…(1-Rn)]

14. Example: Three components are connected in parallel
and make up a system. Component 1 has a reliability of
0.95, component 2 has a reliability of 0.98 and component
3 has a reliability of 0.97 for a mission of 100 hours.
Find the overall reliability of the system for a 100-hr
mission.
Solution:
Rs = 1 – [(1 – R1)(1 – R2)(1 – R3)]
= 1 – [(1 – 0.95)(1-0.98)(1-0.97)]
= 0.99997
= 99.997 %
R1 = 0.95
R2 = 0.98
R3 = 0.97

15. Activity 3A:Computing Parallel System’s
Reliability
0.9
1)
0.8
Rs = 1 – [(1- 0.9)(1- 0.8)]
= 0.98
2)
0.7
0.8
Rs = 1 – [(1- 0.7)(1- 0.8)]
= 0.94

16. Activity 3B: Effect of the Number of Components
in a Parallel System
S
y
s
t
e
m
R
e
l
i
a
b
i
l
i
t
y
1.00
0.90
0.80
0.70
0.60
0.50
0.40
0.30
0.20
0.10
0.00
1 2 3 4 5 6 7 8 9 10
N u m b e r o f C o m p o n e n t s

17. C) Combination of Series and Parallel Structures
Example:
Consider a system with three components. Units 1 and 2
are connected in series and Unit 3 is connected in parallel
with the first two, as shown in the figure below. Find
the reliability of the system.
Solution:
R1 = 0.99 R2= 0.98
R3 = 0.97

18. First, the reliability of the segment consisting of Units 1
and 2 is calculated:
R1,2 = (R1)(R2)
= (0.99)(0.98)
= 0.97
The reliability of the overall system is then calculated
by treating Units 1 and 2 as one with a reliability of
0.97 connected in parallel with Unit 3.
Therefore:

19. R1,2= 0.97
R3 = 0.97
Rs = 1 – [(1 – 0.97)(1 – 0.97)]
= 0.9991
= 99.91%

20. Activity 4: Combination of Series and Parallel
Structure (10 minutes)
R1=0.7
1) R2=0.6
R3=0.5
This is equivalent to:
R1=0.7 R2,3=0.8
Rs = (0.7)(0.8) = 0.56

21. Sample Design Configurations
A. System 1:
A B
C D
Possibilities:
1. If RA = 0.99, RB = 0.99, then Rs = 0.9801
2. If RA = 0.95, RC = 0.95 and RB = 0.99, then RS = 0.997

22. Sample Design Configurations
B. System 2:
A B
C D
Possibilities:
1. If RA = 0.99, RB = 0.99, then Rs = 0.9801
2. If RA = 0.95, RC = 0.95 and RB = 0.99, then RS = 0.9875

23. The Bathtub Curve
Reliability specialists often describe the lifetime of a population of
products using a graphical representation called the bathtub curve.
It characteristically describes the life of many products, as well as
humans.
F
A
I
L
U
R
E
R
A
T
E
Time (hours, miles, cycles, etc)
EARLY LIFE
(burn-in or
break-in or
infant mortality
period)
(failure rate
decreases with time)
USEFUL LIFE
(or normal life)
(failure rate approx. const)
WEAROUT LIFE
(failure rate
increases with time)